聚焦新高考“创新性”研究——第二届命题征集活动函数专题优质创新试题选登

【原创创新试题组】

【原创1】2022年2月,国家发展改革委等部门同意在京津冀等八地启动建设国家算力枢纽节点,并规划10个国家数据中心集群.这标志着“东数西算”工程正式全面启动.在八个节点中,内蒙古、甘肃、贵州和宁夏属于第一类;京津冀地区、粤港澳大湾区、长三角地区和成渝地区属于第二类.现从八个节点中,任取3个节点进行数据处理,且选择任何一个节点是等可能的,则选取的3个节点至多有2个属于第一类的概率为________.

【原创2】《九章算术》中有一种几何体叫刍甍(méng)(底面为矩形的屋脊状楔体),如图1是一个刍甍,图2是其俯视图,其中网格纸上小正方形的边长为1,若其侧视图是等腰直角三角形,则此刍甍的表面积为________.

图1

图2

【原创3】双曲函数是由以e为底的指数函数y=ex和y=e-x所产生的.其定义为:

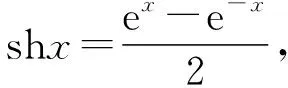
类比三角函数的公式,我们给出如下双曲函数的公式,其中正确的序号为________.

①sh2x+ch2x=1;

②sh(x-y)=shx·chy-chx·shy;

③ch(x+y)=chx·chy-shx·shy;

④sh2x=2chx·shx.

(Ⅰ)记bn=a2n,写出b1,b2,并求数列{bn}的通项公式;

(Ⅱ)求数列{an}的前12项和.

【原创5】如下图,已知在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D,E分别在CC1与AA1上,AE=2.

(Ⅰ)现给以下三个条件,请选择________(只填一个序号),求线段CD的长;

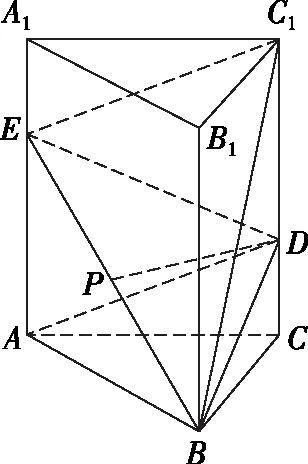
①P为BE的中点,满足DP⊥平面ABB1A1,

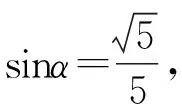
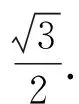
(Ⅱ)在(Ⅰ)条件下,求D到平面BEC1的距离.

【答案详解及创新点分析】

【创新点分析】以“东数西算”工程为背景,对概率进行考查.

(作者单位 姓名:四川省南充市第一中学 陈清方)

【创新点分析】本题在突出主干知识的同时,对题干材料和设问形式的设置上进行了创新:

1.题干材料设置创新:

本题以《九章算术》中的刍甍为背景,打破以往仅仅是对《九章算术》中问题的直接引用和翻译,而是重新设计问题,考查空间几何体的表面积、三视图,渗透数学文化,尤其是中国优秀传统文化,课程思政,展现德育育人.

2.设问形式创新:

打破以往三视图的呈现方式,本题以三视图信息不全的不良结构呈现本题,从直观图和三视图的双重角度考查学生的空间想象能力,进而着力于直观想象核心素养.

(作者单位 姓名:西安交通大学苏州附属中学 陈鸿斌)

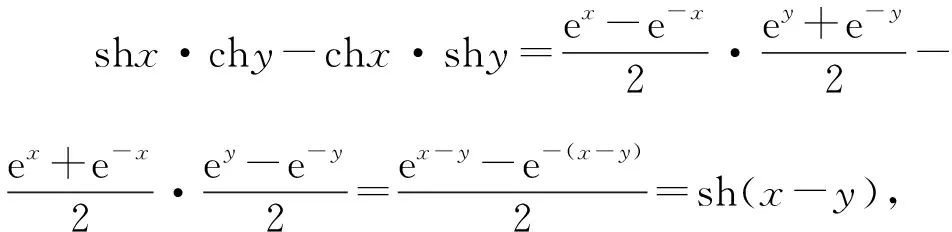
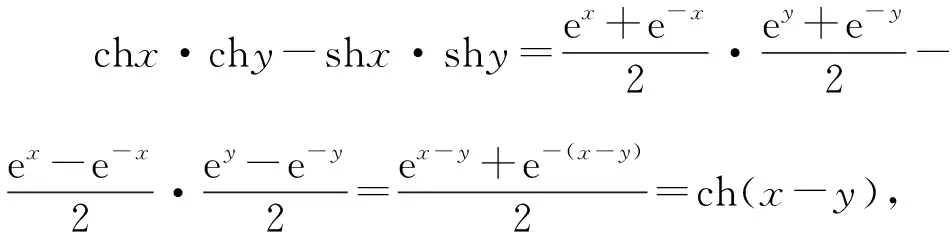
综上,正确公式的序号为②④.

【创新点分析】以重要函数为载体,对新概念“双曲函数”作了解析,考查了新定义.

(作者单位 姓名:四川省南充市第一中学 广元天立学校 成都东辰外国语学校 陈清方 陈朝蓉 赵小庆 雷小芹 陈清文 赵 欢)

【原创4】【解题思路】(Ⅰ)由题设得b1=a2=2a1-2=1,

b2=a4=2a3-2=2×(2a2+1)-2=4.

因为bn+1=a2(n+1)=a2n+2=2a2n+1-2=2(2a2n+1)-2=4a2n.

因为bn=a2n,所以bn+1=4bn,即数列{bn}是以b1=1为首项,4为公比的等比数列,

所以bn=4n-1.

(Ⅱ)解法一:由(Ⅰ)知

a2=1,a4=4,a6=42,a8=43,a10=44,a12=45,

43+44)+5

解法二:由(Ⅰ)得a2n=4n-1,

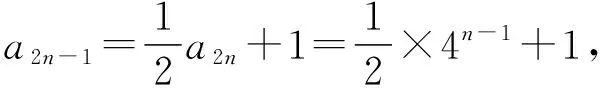
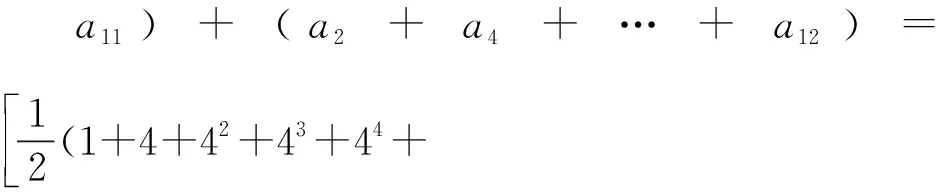
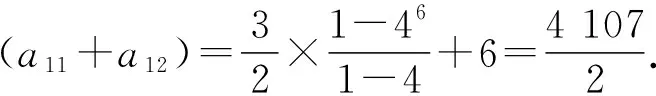
【创新点分析】2021年全国新高考Ⅰ卷第17题,以“奇偶项交织”的递推关系考查数列的基本知识,注重基础,但形式新颖,主要考查等差数列的知识;本题主要考查等比数列的知识,在数学运算上要求更高,同时也在积极引导学生注重由特殊到一般,努力探究出这类问题求数列通项的通性解法.

(作者单位 姓名:广东省汕头市潮南区砺青中学 郑灿基)

【原创5】【解题思路】(Ⅰ)选择①,

取AB的中点F,连接PF,CF,

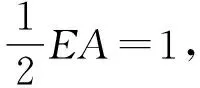
因为EA∥CD,所以PF∥CD.

在正三棱柱中,平面ABC⊥平面ABB1A1,CF⊥AB,平面ABC∩平面ABB1A1=AB,CF⊂平面ABC,所以CF⊥平面ABB1A1.

又DP⊥平面ABB1A1,所以CF∥DP,

所以四边形DPFC为平行四边形,

所以CD=PF=1.

选择②,

因为CD⊥平面ABC,所以∠DBC为BD与平面ABC所成角为α,

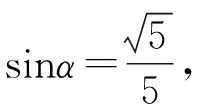
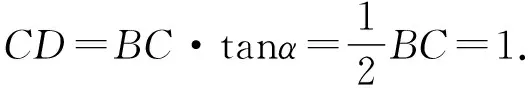
选择③,

取AB的中点F,连接DF,CF,

易得CF⊥AB,

因为CD⊥平面ABC,AB⊂平面ABC,所以CD⊥AB.又CF∩CD=C,

所以AB⊥平面DFC,

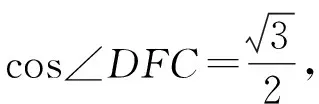
所以CD=1.

所以C1E2+BE2=C1B2,故C1E⊥BE,

设点D到平面BEC1的距离为d,

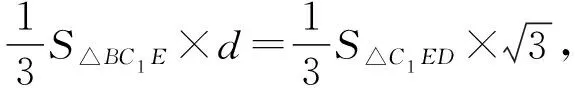
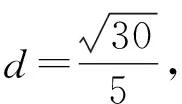
设平面C1BE的法向量为m=(x,y,z),则有

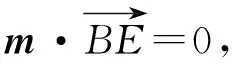
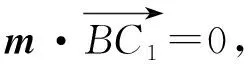
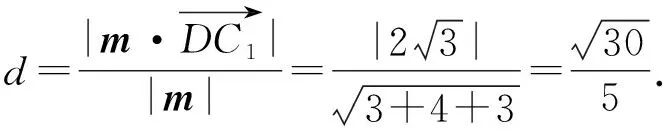
【创新点分析】设问角度上创新:采用逆向形式,由线面垂直、线面角、面面角求线段长;

题型选择上创新:结构不良试题;

考查维度上创新:问题的设置上融入线面垂直、线面角、面面角、点到平面的距离等立体几何的重点;

设问形式上创新:以选择的形式设问,增加开放度.