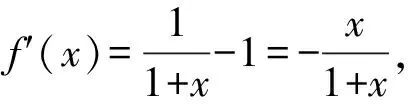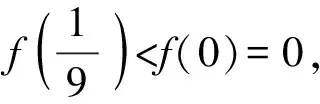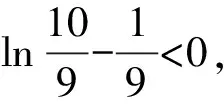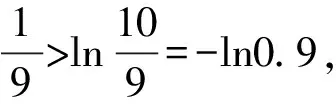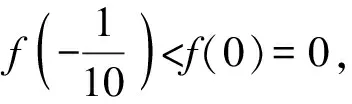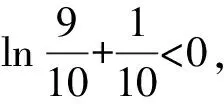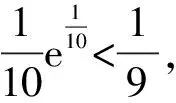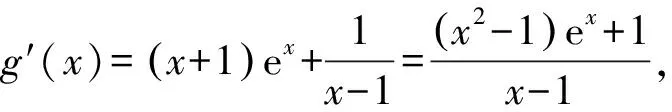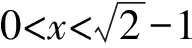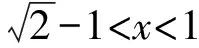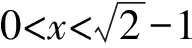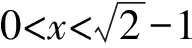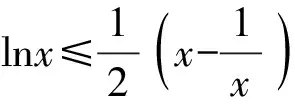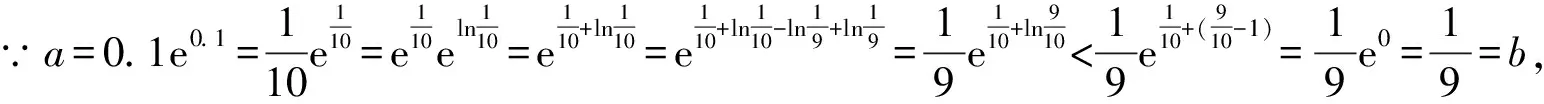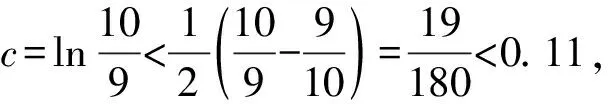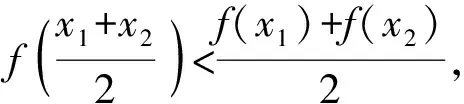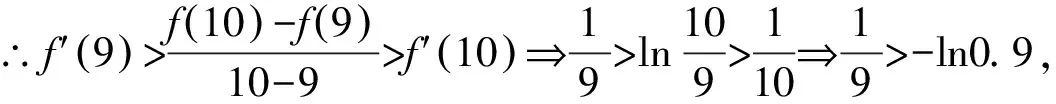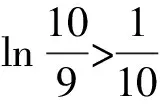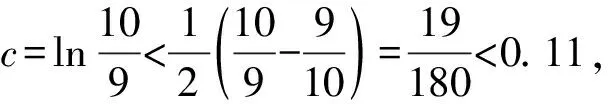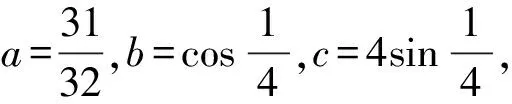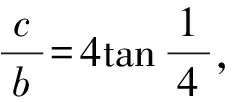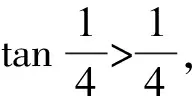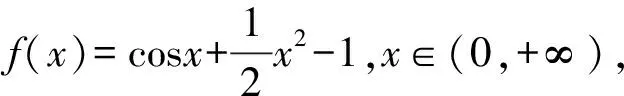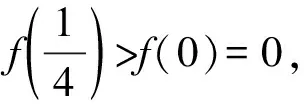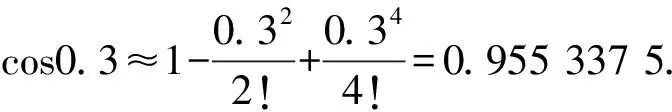数学试题中的隐数学文化——以2022年数学新高考Ⅰ卷第7题为例

来 伟 王 莉

(1.安徽省蚌埠第二中学; 2.安徽省滁州市第二中学)

新高考进入了无纲时代,2022年的数学试题,突出了试题的创新性,优化了试卷的结构,变换了提问的方式,改变了试题结构,增加了试题的新颖性和灵活性,促使学生运用知识解决新问题的能力.返溯2020年,2021年,2022年以及新高考八省适应性训练的一致性和差异性,规律性可能是未来高考的命题趋势,差异性是高考释放的信息,这要求我们更新观念,查缺补漏,新高考倒逼教学改革.

近几年的高考数学中,关于以导数为背景的比较大小的题目,出现频率较高,试题着重考查了学生构造函数,运用不等式,对课本扩展的知识和二级结论掌握程度的综合体现.这些题目往往有着高等数学的背景,使压轴题更具新意,增加了试题的难度和区分度,本文通过2022年高考试题的例题分析,借鉴高等数学的知识,开阔学生的数学思维宽度,以期提高数学思维力.

下面我们以2022年新高考数学Ⅰ卷第7题为例:

( )

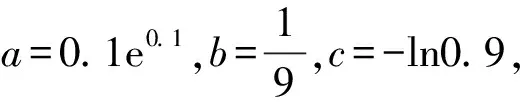
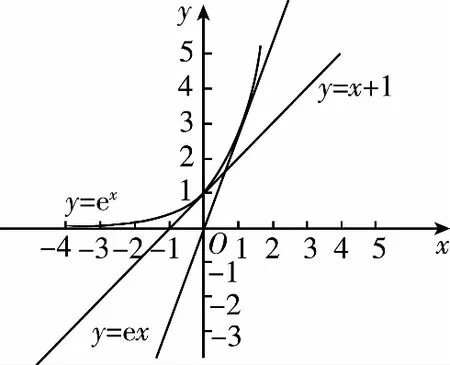
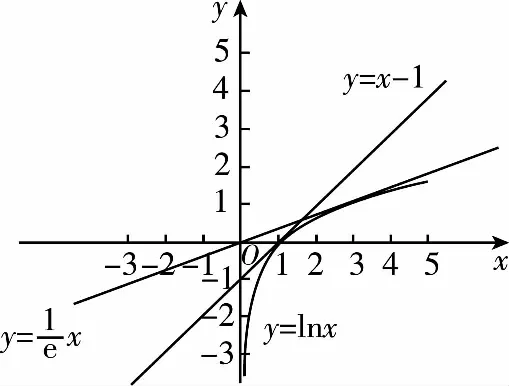
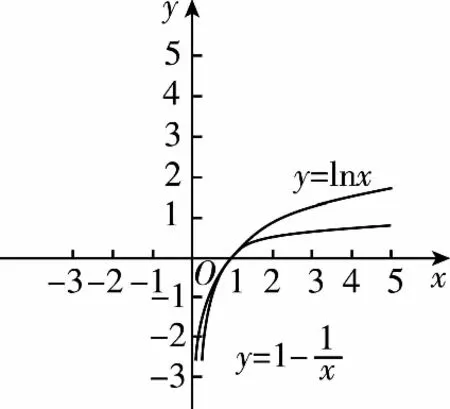
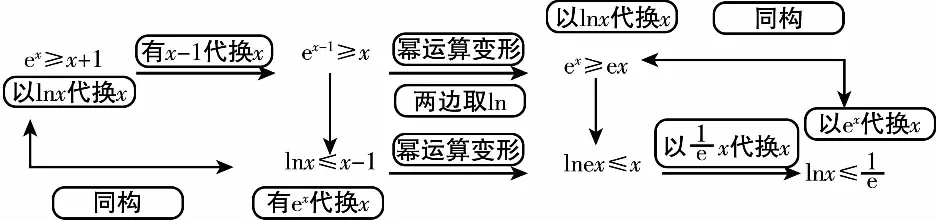
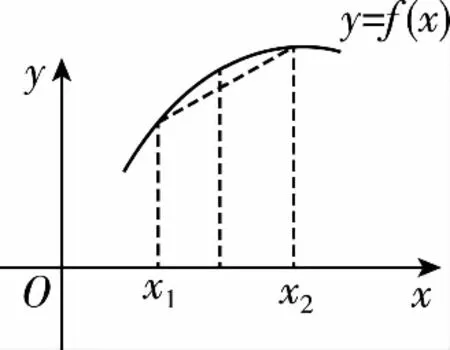
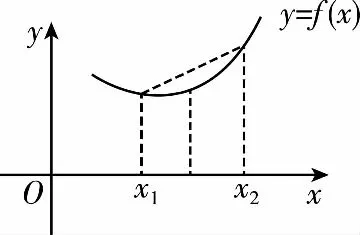
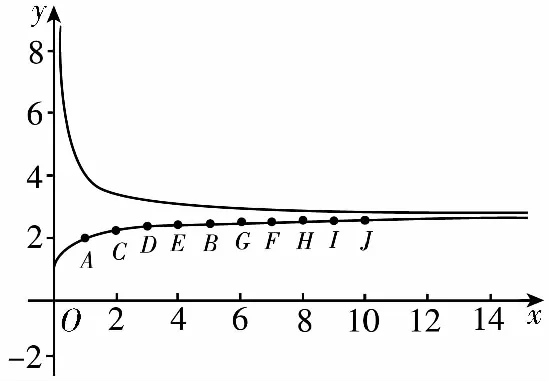
A.a

C.c

方法一:构造函数

设函数f(x)=ln(1+x)-x(x>-1),

当x∈(-1,0)时,f′(x)>0,

当x∈(0,+∞)时f′(x)<0,

所以f(x)=ln(1+x)-x在(0,+∞)上单调递减,在(-1,0)上单调递增,

设g(x)=xex+ln(1-x)(0

令h(x)=ex(x2-1)+1,h′(x)=ex(x2+2x-1),

h′(x)<0,h(x)=ex(x2-1)+1单调递减,

h′(x)>0,h(x)=ex(x2-1)+1单调递增,

又h(0)=0,

函数g(x)=xex+ln(1-x)单调递增,

所以g(0.1)>g(0)=0,即0.1e0.1>-ln0.9,

所以a>c,故选C.

方法二:运用三个重要的不等式:

lnx≤x-1(当且仅当x=1时,等号成立)

ex≥x+1(当且仅当x=0时,等号成立)

①“切线”不等式的图形直观

ex≥x+1 ex≥ex

②“切线”不等式变形转换

∴a

又∵a=0.1e0.1>0.1×(1+0.1)=0.11,

∴c

方法三:利用函数的凹凸性

设f(x)在区间I上有定义.

(1)若对任意的x1,x2∈I且x1≠x2,有

则称f(x)在(a,b)内为凸函数,如图1所示.

图1

(2)若对任意的x1,x2∈I且x1≠x2,

则称f(x)在(a,b)内为凹函数,如图2所示.

图2

∵函数y=lnx是(0,+∞)上的凸函数,

则b>a.

又∵a=0.1e0.1>0.1×(1+0.1)=0.11,

∴c

试题背景:隐数学文化,高等数学重要极限:

比较a与b即0.1e0.1与19即e110与109即110与ln109即1与ln(1+19)10即e与(1+19)1+9比较b与c即19与ln109即1与9ln109即1与ln(1+19)9即e与(1+19)9

本道试题隐含高等数学中函数的凹凸性和重要极限的背景,突出了高中数学知识和大学数学的潜在的联系,以较高的视角,对高考试题进行分析和思考.

( )

A.c>b>aB.b>a>c

C.a>b>cD.a>c>b

f′(x)=-sinx+x>0,

设g(x)=-sinx+x,则g′(x)=-cosx+1≥0,

所以f′(x)在(0,+∞)上是增函数,

所以f′(x)>f′(0)=0,

所以f(x)在(0,+∞)上单调递增,

所以b>a,所以c>b>a,故选A.

【解法二】回归教材:人教A版必修一P256第26题

英国数学家泰勒发现了如下公式:

其中n!=1×2×3×4×…×n.

∴b>a.

∴c>a.

追本溯源:高等数学泰勒公式(曲线逼近,近似计算)

本道试题隐含高等数学中泰勒公式,以课本知识为本源,宽角度,多观点地考查学生的基本素养,有层次的了解学生的理性思维和进一步深造的潜能.