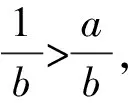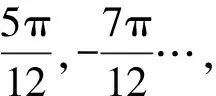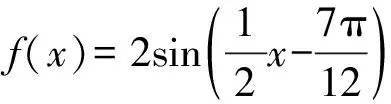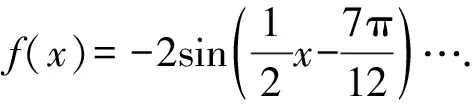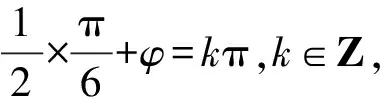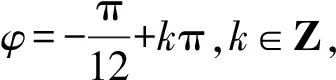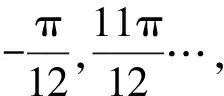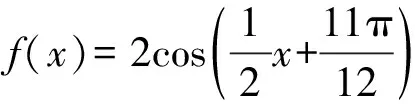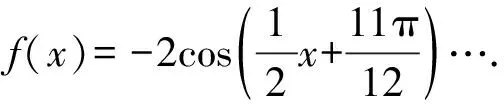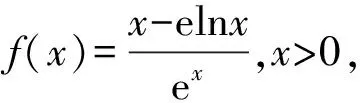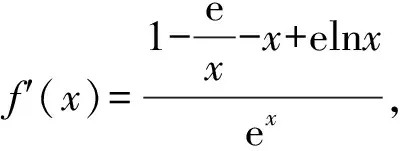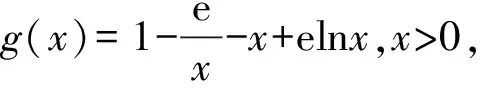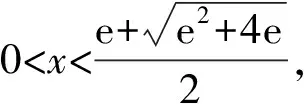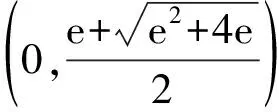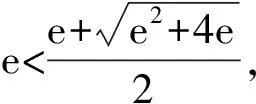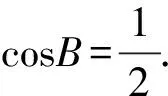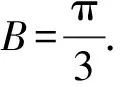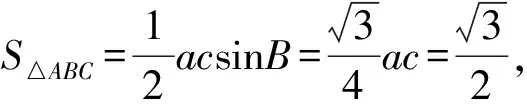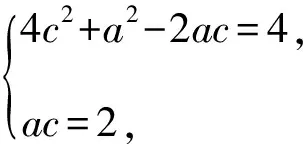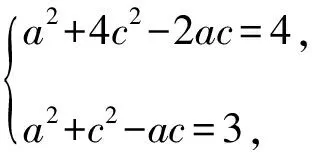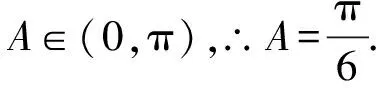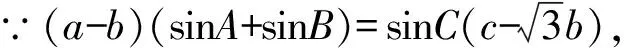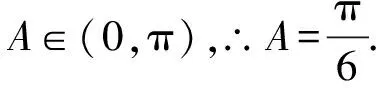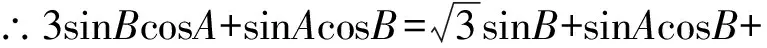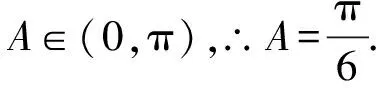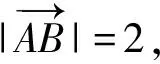聚焦新高考“创新性”研究——第二届命题征集活动函数专题优质创新试题选登

(作者单位 姓名：广西省南宁市第八中学 谢松兴)

(作者单位 姓名：广东省华南师范大学附属中学汕尾学校 袁平红)

(作者单位 姓名：江西省瑞金第一中学 谢小平)

(作者单位 姓名：河南省范县第一中学 石同民)

(作者单位 姓名：广州市南沙第一中学 周艳祖)

【原创创新试题组】

( )

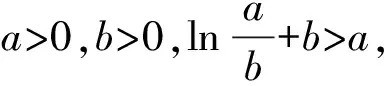
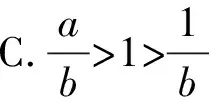
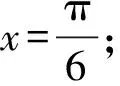
【原创3】若对任意的0ex2+1lnx1-ex1+1lnx2成立,则实数a的最大值为________.

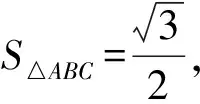
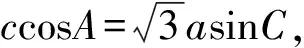
(Ⅰ)求角A的大小;

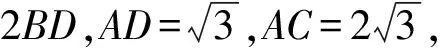
【答案详解及创新分析】

【试题1】【解题思路】

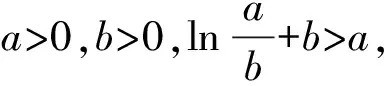
所以lna-lnb+b>a,

即b-lnb>a-lna.

令f(x)=x-lnx,x∈(0,+∞),

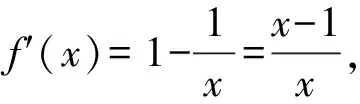
当x∈(1,+∞)时,f′(x)>0,f(x)单调递增,

当x∈(0,1)时,f′(x)<0,f(x)单调递减,

所以当x=1时,f(x)有极小值,

且极小值为f(1)=1,

作出f(x)=x-lnx的大致图象如图所示.

因为b-lnb>a-lna,所以f(b)>f(a),

对于A选项,f(x)在(0,1)上单调递减,

当1>a>b>0时,

故A正确;

对于B,C选项,因为f(x)在(1,+∞)上单调递增,

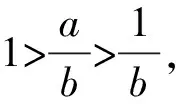
故B正确,C错误;

对于D选项,f(x)在(0,1)上单调递减,

在(1,+∞)上单调递增,对于0

总能找到b>1使f(b)>f(a)成立,

故D正确.

综上,故选ABD.

【创新点分析】本题为多选题,是新高考改革新题型,考查“举例问题”:比较三个式子的大小.数学学科的“举例问题”设问形式灵活,要求考生根据题目给出的要求、性质和定理等条件,从题干中获取信息,整理信息,写出符合题干要求的结论或具体实例,从而增加了试题的开放度.

从知识背景角度上看,本题综合考查对数的图象及其运算性质,利用导数确定函数的单调性,解题的关键点是通过已知条件,构造函数f(x)=x-lnx,利用导数确定函数的单调性,结合不等式的性质比较三个式子的大小,考查考生化归与转化和数形结合的数学思想,考查逻辑推理、数学建模、数学运算的核心素养.

(作者单位 姓名：广西省南宁市第八中学 谢松兴)

【试题2】【解题思路】

若设函数f(x)=Asin(ωx+φ),

由f(x)的最大值为2得A=±2,

所以满足条件的函数解析式可以为

若设函数f(x)=Acos(ωx+φ),

所以满足条件的函数解析式可以为

若设函数f(x)=Asin(ωx+φ)+b

或f(x)=Acos(ωx+φ)+b,

在前两种函数的基础上调整系数A,b的大小,

使得最大值为2,比如A=±1,b=1或A=±4,b=-2,答案不唯一.

【创新点分析】本题属于创新题型,在填空题位置设置开放性问题,答案不唯一.本题以三角函数的性质为背景,反向考查三角函数的性质.传统考查性质的形式是给出函数的解析式,考查函数的性质,多以解答题形式设置,或者给出三角函数的图象求解析式.本题与给出函数图象求解析式有点类似,但是是以填空题的形式来呈现,需要考生对三角函数的图象和性质熟练掌握,同时考查问题的思维方式跟之前也有所不同,即综合函数的性质得解析式.

(作者单位 姓名：广东省华南师范大学附属中学汕尾学校 袁平红)

【试题3】【解题思路】

由x1ex2-x2ex1>ex2+1lnx1-ex1+1lnx2,

得x1ex2-ex2+1lnx1>x2ex1-ex1+1lnx2,

即ex2(x1-elnx1)>ex1(x2-elnx2),

所以当x∈(0,e)时,g(x)<0,即f′(x)<0,

即f(x)在(0,e)上单调递减,

故实数a的最大值为e.

【创新点分析】题干设置简洁精练,设问新颖.因为函数的单调性考查一般是给出的函数解析式中含参,求参数的取值范围,而解答本题首先要找到本题考查的本质,即已知函数的单调性,再用子集观点求参数的取值范围.找本质的关键是对题设的不等式进行变形实现同构,再构造函数(当下热点),考查考生的函数与方程的思想、化归与转化的思想,同时也很好地考查考生逻辑思维的缜密性,充分体现了导数在研究函数单调性中的应用.

(作者单位 姓名：江西省瑞金第一中学 谢小平)

【试题4】【解题思路】

因为acosB-bcosC=(c-a)cosB,

所以2acosB=bcosC+ccosB.

由正弦定理得

2sinAcosB=sinBcosC+sinCcosB=sin(B+C),

因为sin(B+C)=sinA>0,

在△ABD中,由余弦定理得,

AB2+BD2-2AB·BD·cosB=AD2,

整理得4c2+a2-2ac=4.

解得a=2,c=1.

若选②,在△ABC中,

由余弦定理,得a2+c2-2accosB=b2,

即a2+c2-ac=3,

解得a=2,c=1.

【创新点分析】随着旧高考向新高考过渡,新高考出现的新题型也会在旧高考中有所体现,例如结构不良问题,作为一种开放性试题,考查考生的分析理解能力和优化选择意识,是一种能够很好地考查考生数学素养的新题型.

(作者单位 姓名：河南省范县第一中学 石同民)

【试题5】【解题思路】

∵B∈(0,π),∴sinB≠0,

(Ⅱ)解法一:反复运用余弦定理

设BD=x,AB=y,∠ABD=θ,则CB=2x.

在△ABC中,由余弦定理得,

AC2=CB2+AB2-2CB·AB·cos∠ABC,

即12=4x2+y2-2×2x·y·cos(π-θ), ①

CB2=AC2+AB2-2AC·AB·cos∠CAB,

在△ABD中,由余弦定理得,

AD2=BD2+AB2-2BD·AB·cos∠ABD,

即3=x2+y2-2xycosθ.③

由③×2+①可得6x2+3y2=18,

将②代入上式可得y=2,x=1,

解法二:正弦定理+余弦定理

设BD=x,∠ABD=θ,

则CB=2x,∠ABC=π-θ.

在△ABC中,

在△ABD中,

在△ACD中,由余弦定理得,

CD2=AD2+AC2-2AD·AC·cos∠CAD,

∴CD=3,即x=1,

在△ABC中,

BC2=AC2+AB2-2AC·AB·cos∠CAB,

解得AB=2或4(舍),

解法三:用向量方法解决三角问题

【创新点分析】第(Ⅰ)问中的条件以半开放式的形式呈现,结合正弦定理与余弦定理,在三角形的边角之间互化,考查考生解三角形中的必备知识与关键能力;第(Ⅱ)问要求考生敏锐捕捉条件中的重要信息,精准作出图形,创新条件的呈现方式,在解答的过程中,可以利用传统的正弦定理、余弦定理和三角形的面积公式来完成,也可以利用向量方法来解决,向量法解题在运算量方面更具优越性,创新已知条件,从不同角度来分析题目,丰富了解题方法,也体现新高考的变化及趋势.

(作者单位 姓名：广州市南沙第一中学 周艳祖)