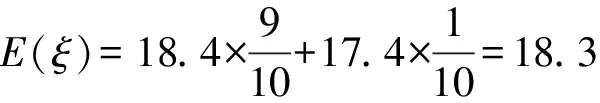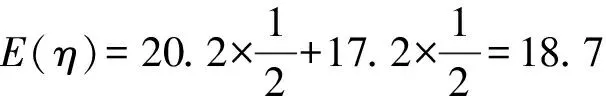基于核心素养的高中数学建模教学的实例探究
潘冬丽 何正文
(1.广东省肇庆市第一中学; 2.广东省肇庆市百花中学)
数学建模作为核心素养一项关键部分,在处理分析实际问题时往往可以做到事半功倍的效果.如果能把问题进行模型化,数据就可以可视化,图形就可以立体化.本文从几个具体数学问题案例中揭示数学建模本质,进而有效培养学生的建模思维.
六个核心素养中数学建模是最难的一环.下面从模型的构建、完善、还原方面进行高中知识层面的实例分析.
一、建立模型构造
高中数学建模构建的核心就是几何与代数的有机融合.突破数学代数结构特征与几何知识相关,能够从数学问题挖掘,构建几何模型去解决.
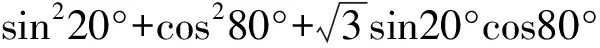

又由余弦定理得,c2=a2+b2-2abcosC,
所以(2Rsin150°)2=(2Rsin10°)2+(2Rsin20°)2-2×4R2sin10°sin20°cos150°,
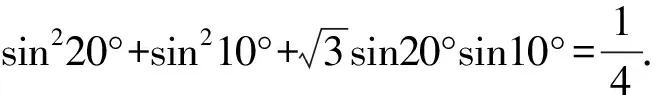
【例2】试证对于任意的正实数a,b,c,
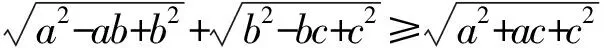
【分析】观察待证式子中的三个根式,容易发现:
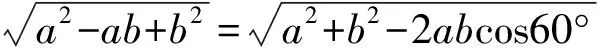
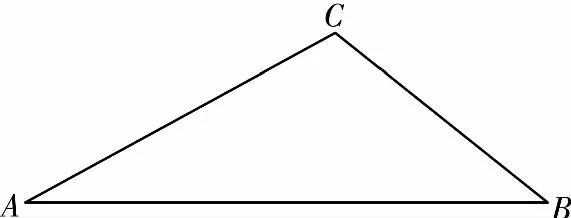
根据上述分析得到如图所示的几何图形模型,

其中AB=c,AC=a,AD=b,
∠CAD=∠BAD=60°,
显然,由余弦定理可知,
在△CDB中,CD+DB>CB是恒成立的,
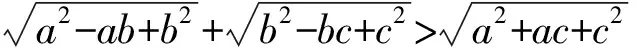
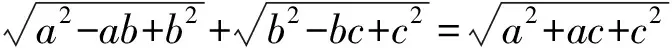
例1,例2分别把三角函数问题、不等式问题转化成对三角形边和角的分析,通过数学建模,解决问题.
常见几何模型有:
(1)|x-a|联想到x到a的距离模型;
(2)(x-a)2+(y-b)2联想到P(x,y)到A(a,b)之间距离的平方模型;
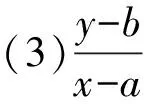

二、突破建模情境
常规问题很难解决时,我们通过在构建数学模型时,调整思维角度,敢于构想新的问题意境,往往柳暗花明又一村.

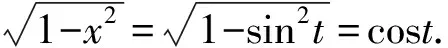

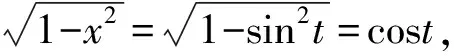
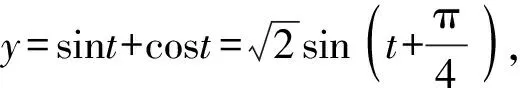

由单位圆知识及函数图象可得
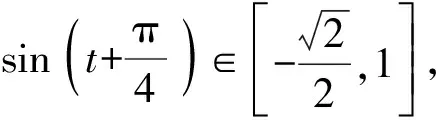

【例4】若关于x的方程|x2-4x+3|-a=x至少有三个不相等的实数根,求a的取值范围.
【分析】我们根据题目带有绝对值,联想距离模型,模型突破点在于把|x2-4x+3|=x+a,分解y=|x2-4x+3|,y=x+a,两个函数图象模型,如图所示.
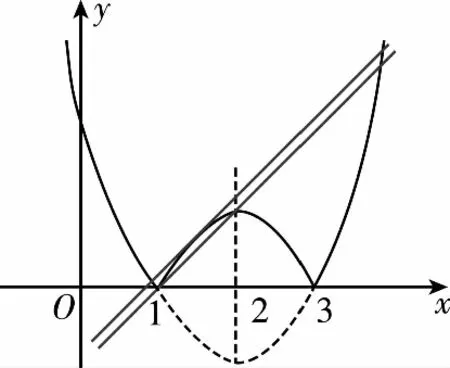
①当a<-3时,由图象可知,函数y=|x2-4x+3|与函数y=x+a的图象无交点,不符合题意,舍去;
②当a=-3时,由图象可知,函数y=|x2-4x+3|与函数y=x+a的图象只有一个交点,不符合题意,舍去;
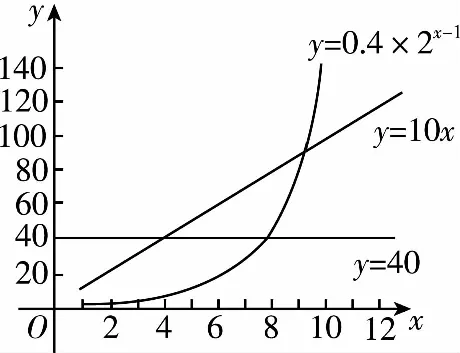
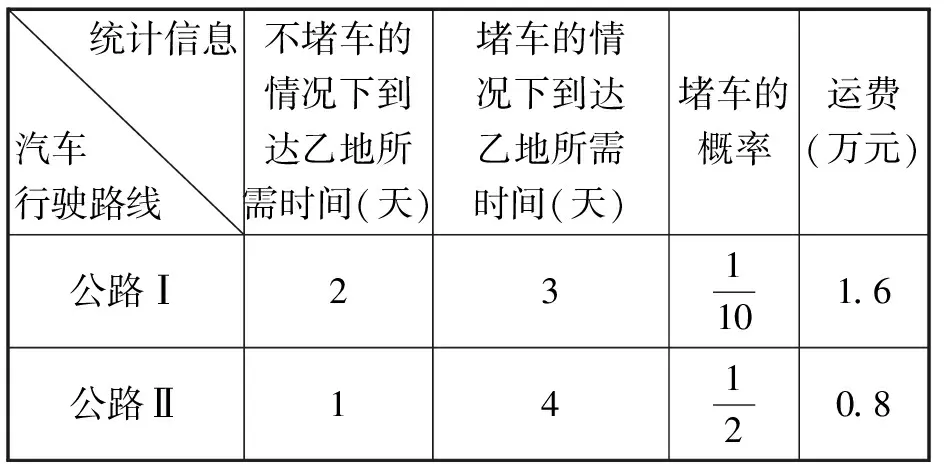
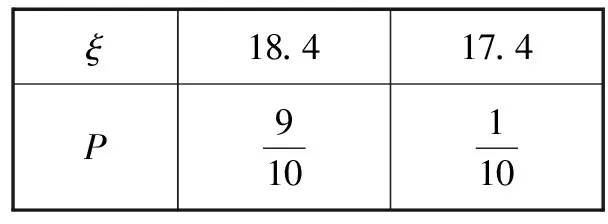
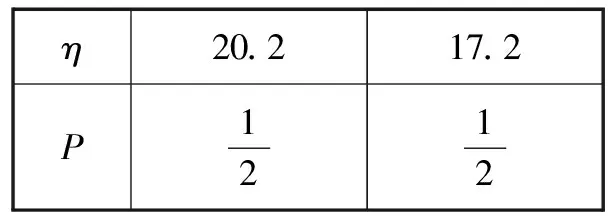
③当-3 ④当a=-1时,由图可知,函数y=|x2-4x+3|与函数y=x+a的图象有三个交点,符合题意. 数学模式讲究数学问题的属性迁移,在数学模型维度解决,回归到认知的问题. 【例5】假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下: 方案一:每天回报40元. 方案二:第一天回报10元,以后每天比前一天多回报10元. 方案三:第一天回报0.4元,以后每天的回报比前一天翻一倍. [问题] 请问你会选择哪种投资方案? 解:设第x天所得回报是y元. 方案一:每天回报40元, y=40(x∈N*),常函数; 方案二:第一天回报10元,以后每天比前一天多回报10元, y=10x(x∈N*),正比例函数; 方案三:第一天回报0.4元,以后每天的回报比前一天翻一倍, y=0.4×2x-1(x∈N*),指数型函数. 通过实际例子让学生利用所学的知识来分析具体的实际问题,并建模解决实际问题.让学生明确数学知识在日常生活中学有所用的事实. 【例6】果农用汽车运一批水果从甲地运至销售商所在乙地.有两条路线,果农承担运费.若准时到,则果农获利20万元;倘若提前送到会有奖励,规定每能提前一天就奖励1万元;如果推迟罚款,每推迟一天罚1万元.但是保证水果新鲜,汽车只能摘下两天内送到.已知下表内的信息: 统计信息汽车 行驶路线 不堵车的情况下到达乙地所需时间(天)堵车的情况下到达乙地所需时间(天)堵车的概率运费(万元)公路Ⅰ231101.6公路Ⅱ14120.8 假设你是果农,你会选择哪个方案? 解:设汽车走公路Ⅰ时,果农获得的毛利润为ξ, (1)如果不堵车, 利润ξ=20-1.6=18.4(万元); (2)如果堵车, 利润ξ=20-1.6-1=17.4(万元). ξ的分布列为 ξ18.417.4P910110 设汽车走公路Ⅱ时果农获得的毛利润为η. (1)如果不堵车, 利润η=20-0.8+1=20.2(万元); (2)如果堵车, 利润η=20-0.8-2=17.2(万元). 利润η的分布列为 η20.217.2P1212 故选择公路Ⅱ运送水果有可能让果农获得的毛利润更多. 本题选材于还原离散型随机变量均值问题模型,背景鲜活真实,具有与生活、生产密切相关的参考价值.考查利用数据建模应用能力.根据表中的数据,毛利润即销售商支付给果农的费用减去运费,再利用均值公式分别得出走公路Ⅰ和公路Ⅱ获得毛利润的均值,由上计算得E(ξ)
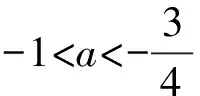
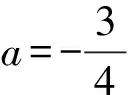
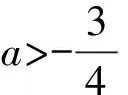
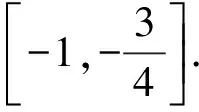
三、回归数学模型还原