素养导向下的习题探究
——以解析几何中的“三定”问题为例
刘祥云 黄小燕
(江苏省兴化中学)
数学习题的探究活动不仅能够帮助学生更好地掌握知识技能,更能帮助学生学会数学思考和实践,是学生形成和发展数学学科核心素养的有效载体.事实上,习题对于学生而言,已经成为了掌握知识,提升能力的唯一途径.习题做错了匆匆地订正一下,就急着去做下一个习题,在一次次的作业和纠错中逐渐丧失了学习兴趣与动力.展开习题的探究活动,是提升学生高阶思维和学习能力的重要手段,所以在平时的教学过程中,教师要引领学生对习题进行深度思考和探究,让学生真正地学会学数学.
1.探究解法,追求自然

【解析】设直线l的方程为x=my+2,点M(x1,y1),N(x2,y2),

消x整理得(3m2-1)y2+12my+9=0,

由题可得F(2,0),A1(-1,0),A2(1,0),



对于(*)式的化简,有以下三种方法:



=-3.


=-3.

【评注】本题是我校一次平常测试中的试题,位于试卷的最后一题,得分率较低.本题中直接影响计算的难易程度就是(*)式的转化路径,方法一是利用韦达定理,把根与系数的关系不对称形式,转化为对称形式,方法二是想实现和与积之间的转化,所以由韦达定理提炼出和与积之间的关系,将积转化为和,得到定值,方法三想把变量m表示出来,再进行代换,从而得到定值,三种解法算理清晰,目标明确,每种转化方法都来自于自然想法,合情合理.
2.探究背景,把握本质
为了探究问题的背景,将题目中的双曲线一般化,通过计算发现定直线即为右准线,得到命题1.
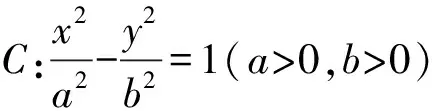

在高观点下探寻数学本质,有一览众山小的感觉,此时又有意犹未尽的感觉,根据极线与极点的知识,将双曲线推广到有心圆锥曲线,很容易的发现下面两个命题(命题2与命题1的极线证明类似,不再赘述).



3.探究定值,提升“四能”

【证明】设直线l的方程为x=my+c,点M(x1,y1),N(x2,y2),

得(m2b2-a2)y2+2b2cmy+b4=0,





因此,在同一道习题中,同时探究生成了定直线、定点、定值问题,但上面的证法不利于将该性质在圆锥曲线中进行推广,故根据两个斜率之积联想到两根之积,可以构造“齐次式”方程,用韦达定理来证明.
【另证】设直线l的方程为x=my+c,点M(x1,y1),N(x2,y2),

双曲线方程可变为b2(x+a)2-a2y2-2ab2(x+a)=0,



4.探究应用,破旧立新



(1)求E的方程;
(2)证明:直线CD过定点.


解析几何的两大作用是建立曲线方程和利用曲线方程研究几何性质,而这两个作用都对数学运算提出了很高的要求,曲线中的定点、定直线、定值三个问题也成为了解析几何中经典的“三定”问题,新课程标准中核心素养学业水平二要求针对计算问题,要合理选择计算方法,设计运算程序,运算求解.其中合理选择计算方法的目的就是减少运算量,提高运算的正确率,这与高考中所提倡的“多考一点思考,少考一点运算”是相一致的.提升运算能力并不是通过试题简单的堆积,要经过数学探究活动发挥出每道试题的最大效用,在每道试题的探究中不断提升自己的探究能力和运算水平,逐渐学会学数学的方法,提升自身的核心素养.

