立足学情精准教学,提升素养科学备考
——“利用奇偶分类讨论解决一类数列问题”的教学反思
周舒仪
⦿常州市戚墅堰高级中学
1 基本情况
1.1 学情分析
本节课的授课对象为常州市戚墅堰高级中学高三理科班学生.在前阶段的学习中,学生已完成了数列专题的一轮复习,熟练掌握了等差数列、等比数列这两类基本数列的定义、通项公式与求和公式,并能根据已知数列的特点选择合适的方法处理求通项以及求和问题; 同时,学生具备一定的观察、分析、归纳、猜想能力.在数列的专题复习中,学生对于利用奇偶分类讨论解决的数列问题有畏难情绪,往往难以识别题型,分析能力较弱.
1.2 内容分析
在高中数学教学内容中,数列占据着知识汇合点的地位,很多知识点都与数列有着密切联系.在课堂教学中,教师要引导学生将数列单元知识进行串联、整合、重构,帮助其形成完整的知识体系,以期达到复习的真正目的.同时,本节课体现的数学思想方法,贯穿于数列全章乃至整个高中数学学习过程中,如分类讨论思想、函数与方程思想、数形结合思想等,对学生数学核心素养的提升也起到了关键性作用.
2 教学过程实录
2.1 回顾数列旧知,复习巩固,建构体系
师:前两周,我们对数列进行了一轮复习梳理,请问本单元复习了哪些知识点?
生:复习了数列的概念、通项公式、递推公式与求和方法.重点研究了等差和等比数列,以及利用数列的递推公式求通项公式与数列前n项和的方法.
2.2 解读高考真题,追本溯源,引入课题
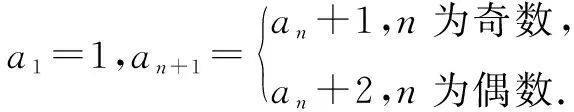
(1)记bn=a2n,写出b1,b2,并求数列{bn}的通项公式;
(2)求数列{an}的前20项和.
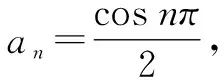
2.3 挑战真题改编,自查互纠,理解运用
例2(2014年新课标Ⅰ卷理科题改编)已知数列{an}满足a1=2,a2=-1,an+2-an=4,求数列{an}的通项公式及前n项和.
师:这个数列的递推公式有什么特征,为什么想到要利用奇偶分类讨论解决?
生:隔项成等差数列.
师:根据前面的经验,观察数列递推公式,发现这个数列的奇数项和偶数项分别成等差数列,所以要分奇偶讨论.你能说出这两个等差数列的基本量吗?
生:数列{an}的奇数项依次构成首项为2,公差为4的等差数列;偶数项依次构成首项为-1,公差为4的等差数列.
师:当n为偶数(n=2k,k∈N*)时,数列{an}的第n项是偶数列中的第几项?
生:当n为偶数(n=2k,k∈N*)时,数列{an}前2k项中,有k个奇数项,k个偶数项,数列的第n项是偶数列中的第k项.
师:当n为奇数(n=2k-1,k∈N*)时,如何考虑项数问题?
生:数列{an}前2k-1项中,比前2k项少一个第2k项,即少一个偶数项,所以其中有k个奇数项,k-1个偶数项,数列的第n项是偶数列中的第k项.
师:数列{an}的通项公式明确后,选择何种求和方法?
生:数列{an}的通项公式以分段形式呈现,应选择分组求和法.
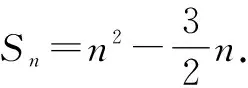

师:这种方法容易出现什么错误?请观察PPT上同学们的做题过程,同桌讨论,找一找他的错误,并思考为什么会出现这样的错误.
学生热烈讨论,分别指出错误.
2.4 剖析变式本质,模型巩固,认识升华
例3已知数列{an}满足a1=2,an+an+1=4n-3,求数列{an}的通项公式及前n项和.
师:数列{an}的递推关系式有什么特征?该如何处理?
生:左侧为连续相邻两项和的形式,右侧为等差数列通项形式.通过递推公式发现,此数列也是隔项成等差数列的模型,也需要利用奇偶分类讨论来解决.
师:掌握了前两个递推公式模型,你能对利用奇偶分类讨论解决数列求通项以及求和问题进行小结吗?四人一组进行讨论.
小组讨论,但不够全面.
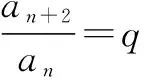
(2)对于递推公式形如an+1+an=dn+b(d,b为常数)的数列,可根据递推公式得
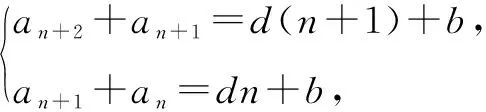
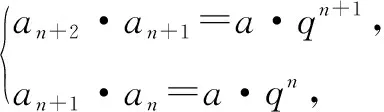
2.5 复盘课堂内容,链接高考,达成目标
师:回到例1,题干中递推公式是直接分奇偶进行分类呈现.请同学们根据bn=a2n,写出b1,b2;再多写几项,找到数列{bn}通项的规律,猜想并验证.
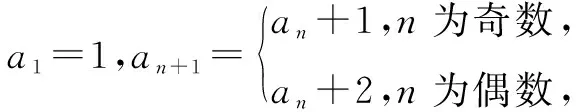
师:由第(1)问,可知bn=a2n=3n-1,n∈N*.如何求出数列{an}的通项公式?
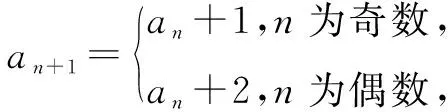
师:根据数列{an}通项公式的特点,请选择合适的求和方式,求出数列{an}的前20项和.
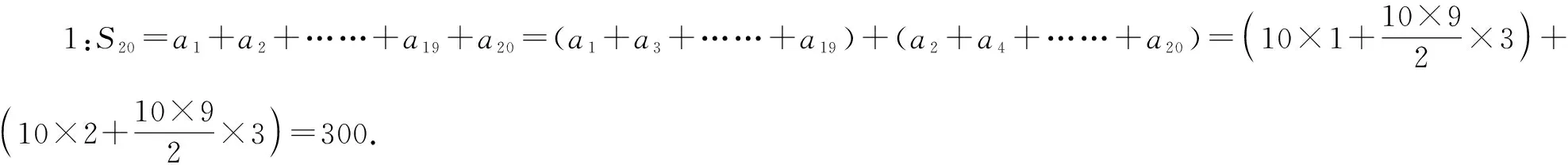
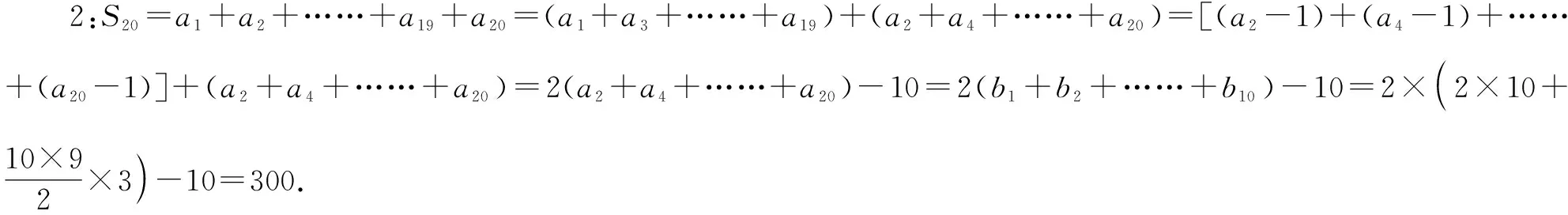
师:非常好!同学们对数列{an}和{bn}的理解都达到了不错的程度,现在将问题进行拓展,你能求出n为偶数时数列{an}和前n项吗?
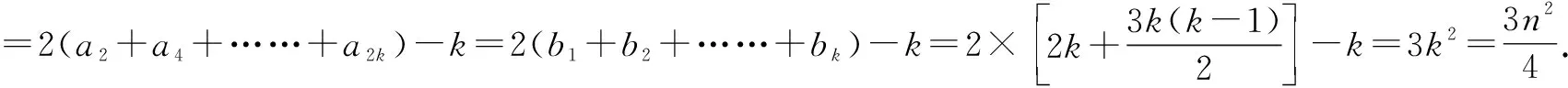
2.6 以自主评价为主线,梳理方法,总结提升
师:现在大家已经可以熟练处理需要利用奇偶分类讨论解决的数列问题了,请同学们复盘本节课内容,对课堂内容和自己的掌握情况做一个总结.
生:本节课学习了三种根据数列递推公式求通项以及数列求和问题.通过本节课的学习,我们可以识别该题型,并能通过递推公式求出数列的通项公式,以及根据数列通项公式选择合适的求和方法.
师:很好!大家都对自己的掌握情况做了客观的评价,在和其他同学交流的过程中,我们也得到了更多的信息和反馈.希望大家能在自评和交流的基础上,加深对新内容的认识、理解、掌握和应用,进一步总结提升.
3 教学反思
高考评价体系由“一核”“四层”“四翼”组成.它的提出和实施,标志着高考评价理念向“价值引领、素养导向、能力为重、知识为基”的综合评价进行转变.根据高考评价体系的整体框架,结合新课标提出的学科核心素养,高考数学提出5项关键能力:逻辑思维能力、运算求解能力、空间想象能力、数学建模能力和创新能力[1].
根据高考评价体系和新课改的要求,本节课从2021年新高考Ⅰ卷第17题数列问题出发,探讨利用奇偶分类讨论的一类数列求通项以及求和问题.利用小闲平台,从学情出发,精准教学;从高考题出发,追本溯源至课本上的习题,再结合多道变式题,通过多种形式反复练习分奇偶讨论的数列的通项公式与前n项和的求法,使学生对这一类数列题的解法体系有了深刻的认识;最后,再回到高考题,实战演练.反思本节课的教学过程,优点在于立足学情,精准教学,有针对性地解决学生问题.同时,选题全部选用高考题及高考题的变式,贴近高考要求.不足之处在于,学生活动设计的不够多,后续还需加强巩固.
高三数学复习是学生查漏补缺、完善知识结构、提高问题分析与解决能力、发展数学核心素养的关键阶段.在高三复习中,常使用微专题复习课的形式进行知识重难点的突破.因此在微专题复习课的设计与教学中须注意以下几点.
(1)建构单元知识网络[2]
通过对微专题所属知识板块的整合,该板块的基础知识和典型问题也有机地整合在一起,体现了知识的整体性,有利于学生从整体上把握并理解知识内涵,发展学生多角度分析和解决问题的能力.
(2)培养理性逻辑思维
教学过程中应注重培养学生观察、分析、归纳、猜想、论证能力.在教学中,除了要设计学生在行为上参与的课堂活动外,还须设计学生能从思维上积极参与的活动,提高学生思维能力,培养理性思维和理性精神,这也是数学教学的基本目标之一.
(3)提炼基本数学思想方法[3]
数学方法具有高度的抽象性、概括性,逻辑的严密性,应用的普遍性和可操作性.教师可为学生呈现不同类型的题目,让学生通过观察、比较、猜想、分析等一系列活动理解问题的本质,同时引导学生进行解题总结回顾,概括提炼基本思想和方法,有助于学生数学基本活动经验的积累与完善.

