一次函数图象教学设计
江苏省睢宁县第二中学
白文波
“一次函数”在初中数学中占据着重要的地位,《义务教育数学课程标准》中对一次函数的教学提出了更高的要求,具体来说要求能画出一次函数的图象,并根据它的图象和表达式y=kx+b(k≠0)探索自变量x的系数k在取不同的值时函数图象对应的变化.基于此,本文中以一次函数图象教学为例,探讨初中数学一次函数的教学设计,以期为教学提供助力.
1 情境引入
众所周知,一次函数y=kx+b(k≠0)的图象是一条直线,主要说明了以下两点:第一,满足y=kx+b(k≠0)的任何一组x,y的值(横、纵坐标)对应的点都在这条直线上,这说明了一次函数y=kx+b(k≠0)的完备性;第二,这条直线上所有点的横、纵坐标(x,y的值)都满足这个表达式,这说明了一次函数y=kx+b(k≠0)的纯粹性.显而易见,这两个方面对初次接触函数的学生来说,有一定的难度.因此,在部分教材中将一次函数的教学目标主要设置为“感知”,规避难点,以常规的“列表、描点和连线”三步操作,不断引导学生观察一次函数y=kx+b(k≠0)的图象,但对为什么满足y=kx+b(k≠0)的点构成的图形就是一次函数的图象没作出任何理解性说明.但以“列表、描点、连线”的方式得出的图象就说其为一次函数的图象是解释不通的,会使学生感到突兀,最终导致不能很好地理解一次函数的知识,从而影响后续其他知识的学习;即便通过强化练习能让学生从感官上接受一次函数的图象是直线,但学生在理解上仍然存在着一定的障碍.
那么,怎样才能引导学生正确理解一次函数y=kx+b(k≠0)的图象是一条直线呢?首先,要从实际情境引入,从动态的直线着手,找到理解一次函数图象就是直线的切入点.一般来说,点动成线,但点动未必成直线,只有点沿着某一个固定方向或其反方向运动时,点的运动轨迹才是直线.因此,想要说明一次函数的图象是直线,亦可以说一次函数图象上点的运动轨迹是直线.其次,从函数图象的倾斜程度入手进行深度理解.实际上,想要说明点动态生成的直线方向是不变的,可从点的运动轨迹入手,说明其与一条特定的直线平行,即一次函数图象上任意一点与其经过的定点的连线和一条特定直线平行.根据直线倾斜角的定义可知,一次函数图象上任意一点和其与x轴(横轴)交点的连线,倾斜角相同,因此可以说明一次函数y=kx+b(k≠0)上的点确实是在一条直线上,也充分体现了一次函数y=kx+b(k≠0)中,k的值决定了直线的倾斜程度,b的值确定了直线和纵轴的交点坐标.为了降低学生的学习难度,教师可以不介绍倾斜角的相关概念.下面以引入实际情境的问题为例,更好地帮助学生理解一次函数y=kx+b(k≠0)的图象是一条直线.
问题1播放一段视频,在视频中顾客头顶系的蝴蝶结的运动路线是怎样的?
问题2哪位同学能说明一下为什么蝴蝶结的运动轨迹是直线?
上述两个问题主要是让学生从实际情境中抽象出点动成线的思维,理解一个点必须要沿着一个指定的方向进行运动,其运动轨迹才能是一条直线,为后续课程的学习奠定基础.
2 完善知识体系
复习相关数学知识时,教师要积极寻找知识间的联系,使学生完善知识,并通过递进型的问题串将知识点串联在一起,促使学生形成知识结构网络.在选择习题方面,教师要重点关注问题之间的关联性,引导学生打破知识壁垒,寻找不同的解题方案.下面以三个习题为例,说明完善知识体系的重要性.
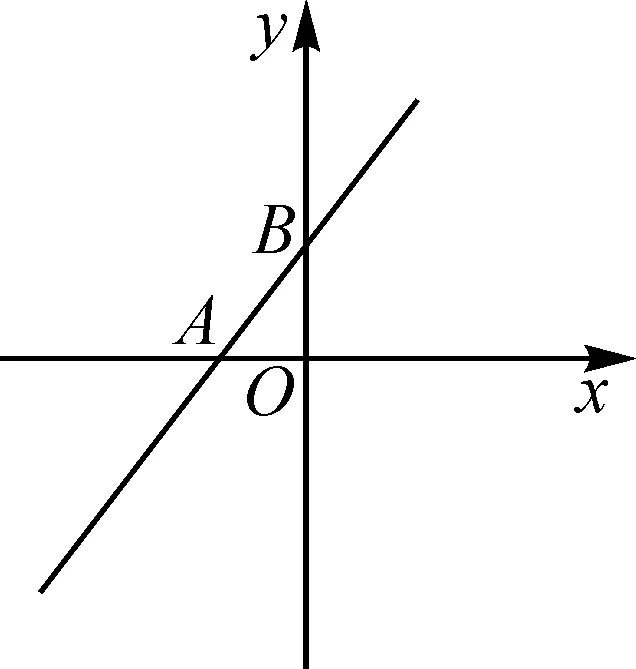
图1
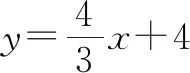

图2
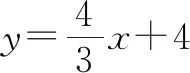
(1)求B′的坐标;
(2)求直线AM的解析式.
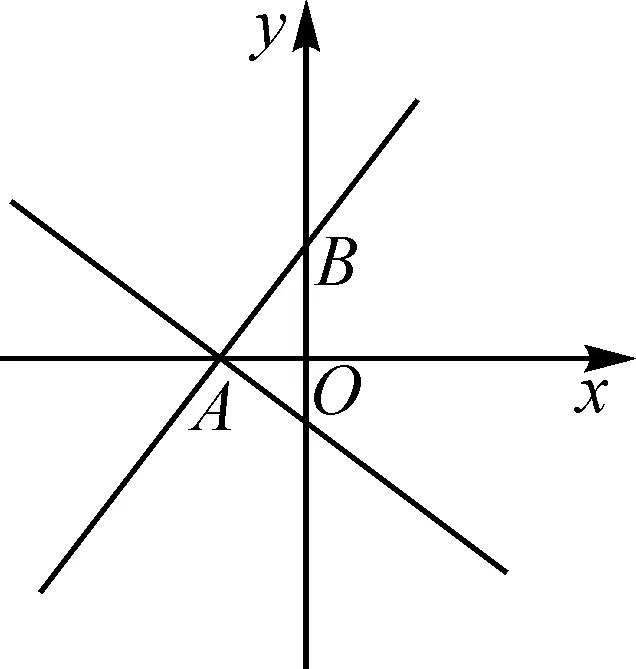
图3
通过以上三道例题,将课程的讲解推向高潮,把学生的思维引领到更深的层次.通过旋转、平移、对称三大变换,引导学生从不同的层面解决实际问题,寻找变换中的不变量,使学生最终领悟到图形的变换本质,培养学生思维的灵活性.
3 开展实际应用
数学教师的主要职责就是尽可能开拓学生解决实际问题的能力.学生是在动态环境中学习数学,也能在动态中生成数学思维.通过呈现真实的情况,提出思考价值高的问题,进一步厘清学生的认知结构,促使学生在掌握基本技能和基础知识的同时,还能增长解决实际问题的能力.
在应用中,教师可在学生看图、思图、议图的过程中,对学生提出问题,培养学生的创新意识和发散思维.

图4
例4一列快车从甲地开往乙地,一列慢车从乙地开向甲地,两辆车同时出发,假设慢车的行驶时间为xh;两辆车之间的距离为ykm,图4的折线表示y与x之间的函数关系,请根据图象探究以下问题:
(1)甲乙两地之间的距离;
(2)解释途中B,C,D点的实际含义;
(3)还能从图中得到哪些信息?
例4通过将图形作为背景,探究了以一次函数为基础背景下的实际行程问题.通过看图、思图、议图,反思题目的解决办法,促使学生明白“数形结合”思想、方程思想等.最后教师再引导学生大胆提出问题,不仅能提高学生将实际问题变换成数学问题的能力,还能培养学生的发散思维、创新意识和探究能力.
4 教学反思
一次函数是学生在初中阶段初次接触的函数,因此,学习经验的总结和积累是十分重要的.把学习一次函数积累的经验运用到学习其他函数的过程中,是一种很重要的能力.主要体现在以下几个方面.
4.1 建立全新的研究思路
当学习一种全新的函数时,研究函数性质起关键性的作用,函数图象则是一种研究函数性质的工具.从图象的特性着手探索函数的本质,真正体会到函数的实际变化规律.例如,学生在以后学习正比例函数时要关注函数图象的大致变化趋势,根据观察能发现函数的增减性;在函数变化趋势相同的情况下,又观察发现图象的陡和缓能影响函数值的变化速度;等等.本质上就是充分研究函数的性质,以及函数表达式中自变量前面的系数与函数图象的关系.虽然说函数种类不同,但所有的函数题目考查方式都是差不多的,用推衍出的思路研究类似的函数对象是一种很重要的能力.
4.2 “数形结合”思想
“数形结合”思想是研究函数最重要的思想,在绘制函数图象的过程中要时刻分析解析式.例如在观察解析式y=2x时,要根据y随x的变化对函数整体的趋势有大致了解.而在利用函数图象总结相关性质时,要注重函数基本特征的代数表达,正确引导学生发现函数的变化规律.以上操作就是“数”和“形”之间的相互转换,让学生自行体验从抽象到具体,从特殊到一般的思想.
总之,让学生更好地理解一次函数是一次函数的教学重点、同时也是难点.不能因为它是难点,就回避问题,而要像本文所设计的一样,在学生理解的基础上,结合相关实际情况,因材施教,让学生自主形成发散思维,才是应有的教育态度.

