徐州城区市政排水设计流量计算方法研究
刘占会,牛平平,杨拾璞
(1.徐州金石工程技术咨询有限公司,江苏 徐州 221111;2.徐州市水利建筑设计研究院有限公司,江苏 徐州 221116;3.徐州市规划设计院有限公司,江苏 徐州 221018)
关于市政排水和水利排涝的标准衔接问题,已有很多文章探讨过,可以归纳为3类。①研究市政短历时暴雨量和水利长历时暴雨量之间的匹配关系,进而确定市政和水利的标准衔接。刘俊等[1]从最大1 h暴雨量不超过市政1 h设计暴雨量的降雨过程得到水利长历时最大暴雨量,其重现期即为相匹配的水利排涝标准。谢华等[2]根据平原河网地区市政1 h设计暴雨量占水利长历时暴雨量的百分比确定水利长历时暴雨量,其重现期即为水利最低排涝标准。贾卫红等[3]提出了研究年上海市最大1 h与年最大24 h雨量相融性关系的方法,建立了排水标准和除涝标准衔接的暴雨重现期关系。符锐等[4]从南京市最大1 h暴雨量不超过市政1 h设计暴雨量的水利长历时降雨样本中得到基于破坏率的频率曲线,在频率曲线上读出频率与破坏率一致的设计暴雨量,进而确定标准衔接关系。刘曾美等[5]以市政短历时暴雨量、水利长历时暴雨量是否超过设计暴雨量求解条件概率,得出不同衔接标准下的风险率。②根据暴雨选样方法、流量计算公式的不同,以设计流量确定市政和水利的标准衔接。陈斌[6]运用城建部门排水流量公式、水利部门推理公式法分别计算某片区(集水面积2.94 km2)的排水流量和排涝流量,比较了不同重现期下两种计算方法设计流量的差别。谢淑琴[7]采用城建部门和水利部门常用的计算方法计算广州某小区(集水面积2.84 km2)的设计排水流量,分析产生差别的原因。黄国如等[8]分别利用综合单位线、推理公式、城市水文学和室外排水公式等方法计算深圳市民治河流域(集水面积19.23 km2)设计洪峰流量,结果表明综合单位线法与其他方法所得结果的相对误差均在允许范围内,采用综合单位线法所得结果作为设计成果能够满足城市防洪安全。③基于水动力模型,采用专业软件研究市政和水利的标准衔接。黄国如等[9]利用Info Works ICM构建广州市东濠涌流域(流域面积12.40 km2)管道、河道及地面二维的耦合模型,分析市政排水与水利排涝标准两者之间的衔接关系。严婉玲[10]采用MIKE11水动力模型开展排涝演算,以佛山市三山围(集雨面积10.82 km2)和王芝涌片(排涝面积9.50 km2)为研究对象,探索水利排涝与市政排水标准的对应关系。
早期的研究或从设计暴雨量探讨排水和排涝的重现期对应关系,或从设计流量探讨排水和排涝的重现期对应关系,这些研究基于市政排水暴雨选样采用年多个样法或超定量法,水利排涝暴雨选样采用年最大值法。由于以前国内自记雨量资料不多,因此,市政排水多采用年多个样法或超定量法。随着中国自记雨量资料的完善,越来越多的城市采用年最大值法。最新的研究也注意到了这种变化趋势,并基于水动力模型从设计水位和流量探讨排水和排涝的重现对应关系,但研究对象的汇水面积往往远大于2 km2。上述研究多根据特定的流域面积、坡度得出市政排水和水利排涝的标准衔接,没有考虑面积、坡度二维组合条件下的动态变化情况。市政行业和水利行业的设计暴雨,其降雨历时、重现期有重叠的部分,市政排水管网和特小流域河道的产流、汇流机制具有一定的相似性,因此,本文从工程实践中选取徐州市区4个不同的汇水区域,运用徐州市暴雨强度公式和江苏省暴雨图集等多种方法计算市政排水设计流量,并从工程实例延伸开来,分析各种方法计算结果随面积、坡度、重现期的变化趋势,探讨市政排水和水利排涝的标准衔关系。
1 工程实例与计算方法
1.1 汇水区域概况
西安北路干沟、苏堤北路干沟、煤建路干沟、建国西路干沟等4个汇水区位于徐州老城区,地势平坦,但管道平均坡度均大于7,汇流计算时可按山丘区考虑。4个汇水区域的面积大小不一,但都小于2 km2,形状系数也各不相同,因此选取的研究对象具有代表性。4个汇水区域的末端均是由明改暗的干沟,承担着所在区域主要的排水功能。本文的管道平均坡度、汇水区域形状系数系借用水文学的概念。汇水区域特征参数见表1。

表1 各汇水区域特征参数
从管道坡度比较,汇水区域2、4的管道平均坡度显著大于汇水区域1、3。从形状系数比较,汇水区域4类似扇形流域,汇水区域3类似狭长流域,汇水区域1、2介于两者之间。4个汇水区域的管网概化图见图1。
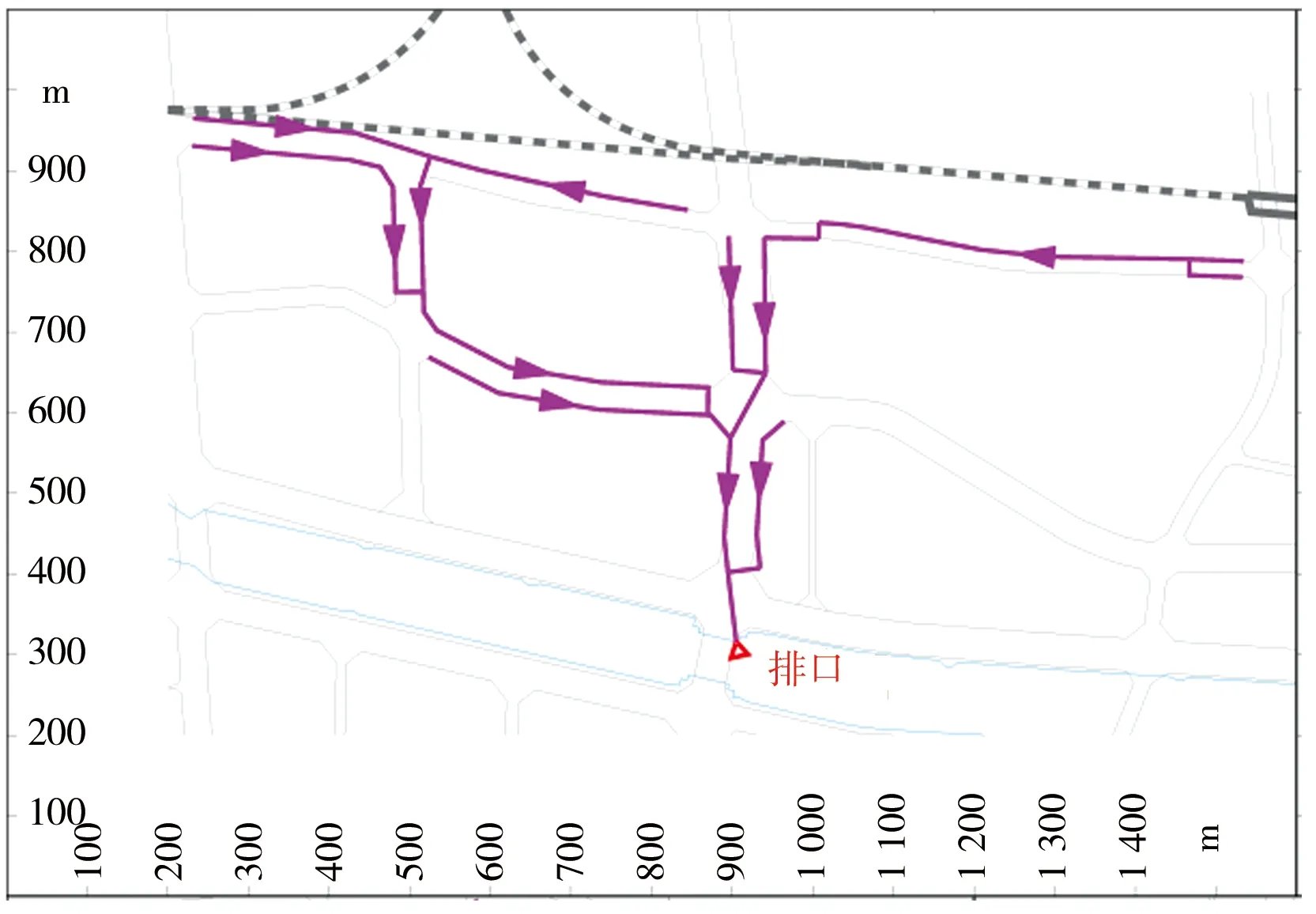
a)西安北路干沟
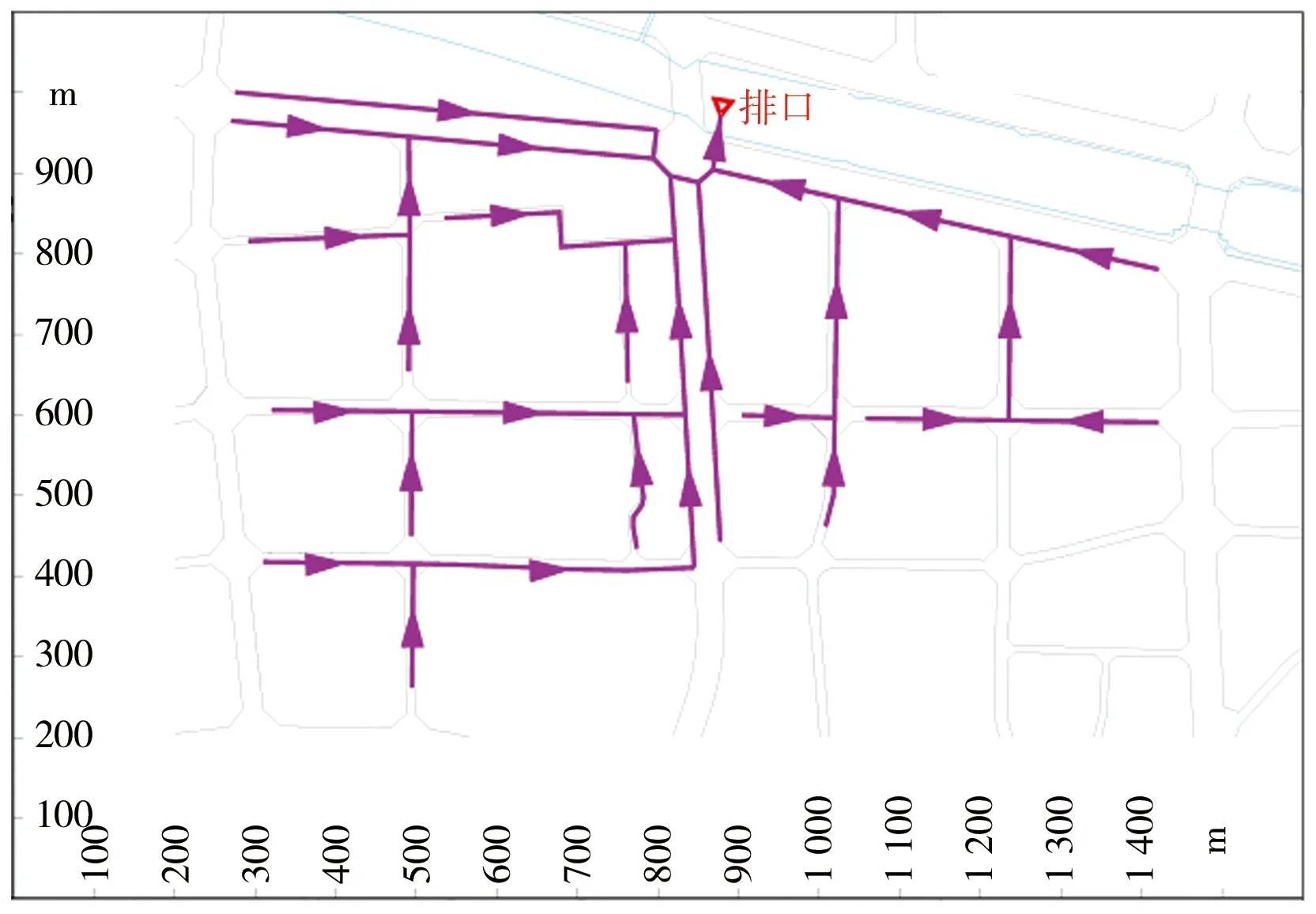
b)苏堤北路干沟
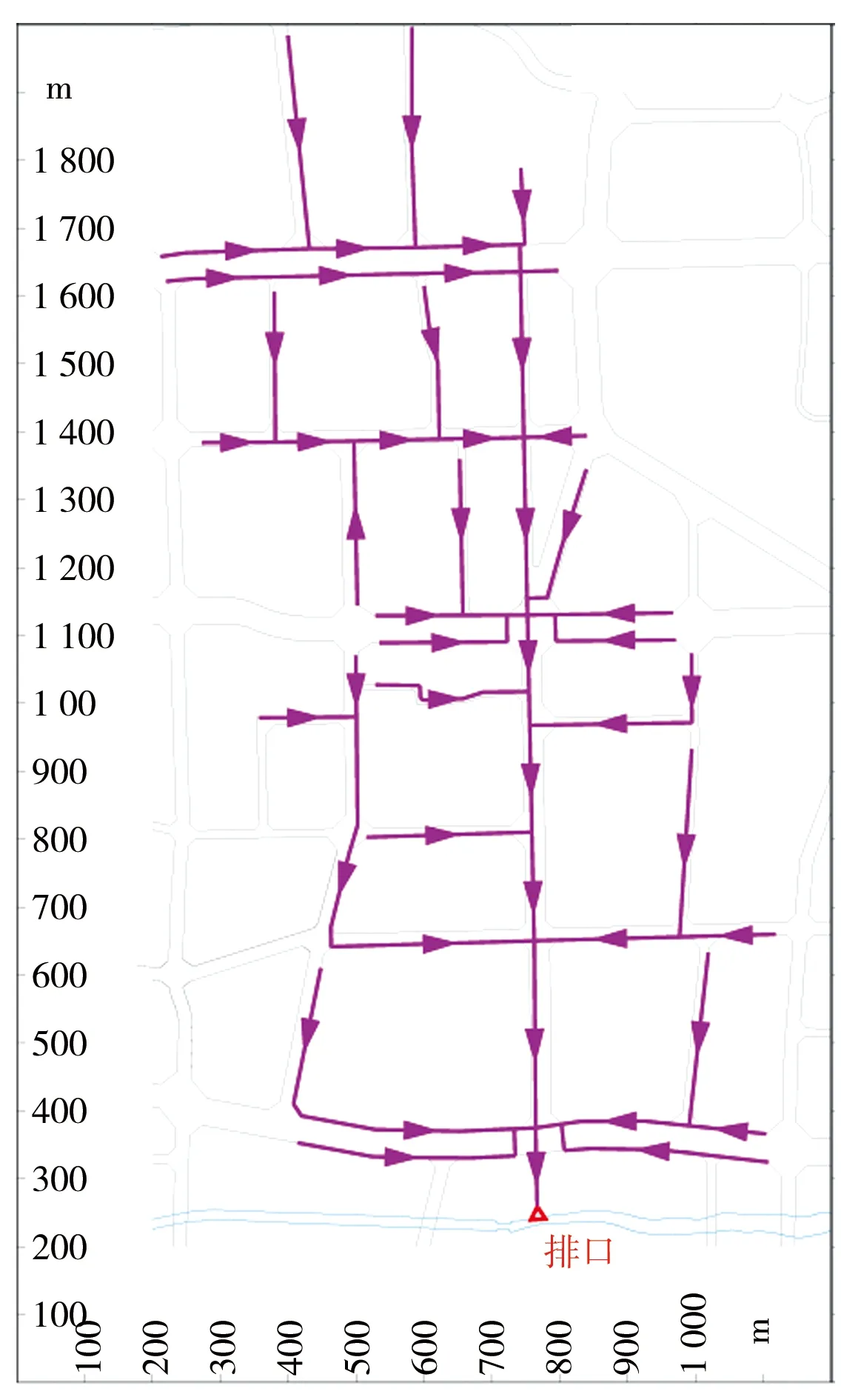
c)煤建路干沟
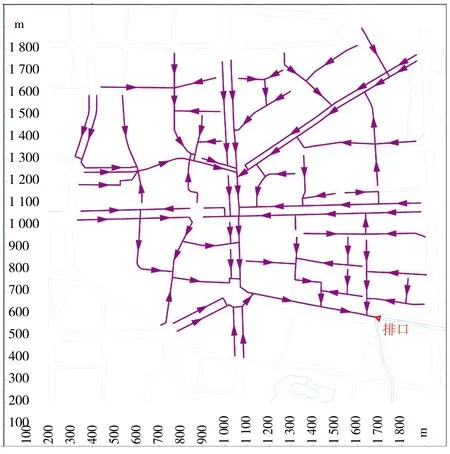
d)建国西路干沟图1 管网概化图
1.2 点雨量计算
市政行业通常采用暴雨强度公式计算设计暴雨量。徐州市现行的暴雨强度公式根据1980—2010年共31 a的降雨资料编制而成,暴雨样本选样采用年最大值法,曲线拟合从皮尔逊Ⅲ型分布曲线、耿贝尔分布曲线和指数分布曲线中选优,求解参数采用高斯-牛顿法[11]。徐州市现行的暴雨强度公式如下:
(1)
式中i——暴雨强度,mm/min;P——设计重现期,a;t——降雨历时,min。
根据式(1)即可计算某一降雨历时某一设计重现期下的设计点暴雨量:
Ht,P=i×t
(2)

(3)

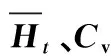
表2 各降雨历时值
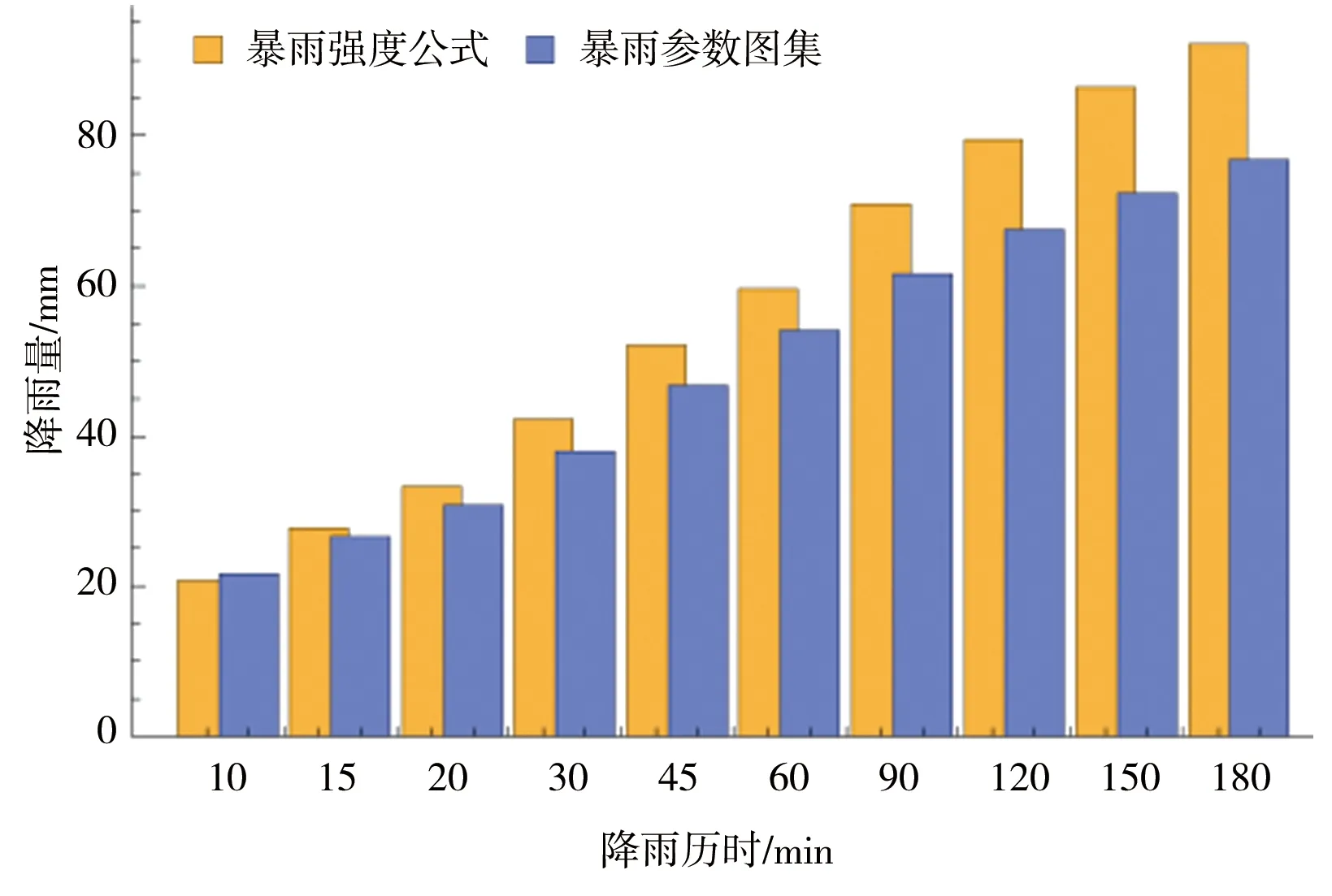
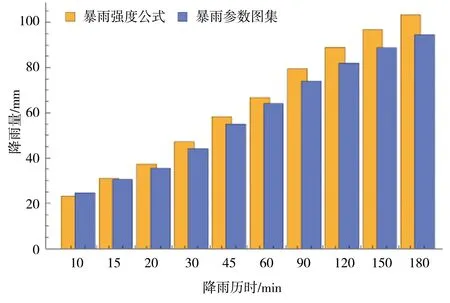
由于《江苏省暴雨参数图集(2005)》短降雨历时只有10、60 min,其余中间时段的点暴雨量用内插法推求。对比上述2种计算点暴雨量的方法,暴雨强度公式的暴雨递减指数n是一个定值,不随降雨历时、设计重现期的变化而变化;而暴雨图集中,不同的降雨历时对应不同的暴雨递减指数,且暴雨递减指数随着设计重现期的改变而改变。推求中间时段的设计点暴雨量内插公式见式(4)—(7)。
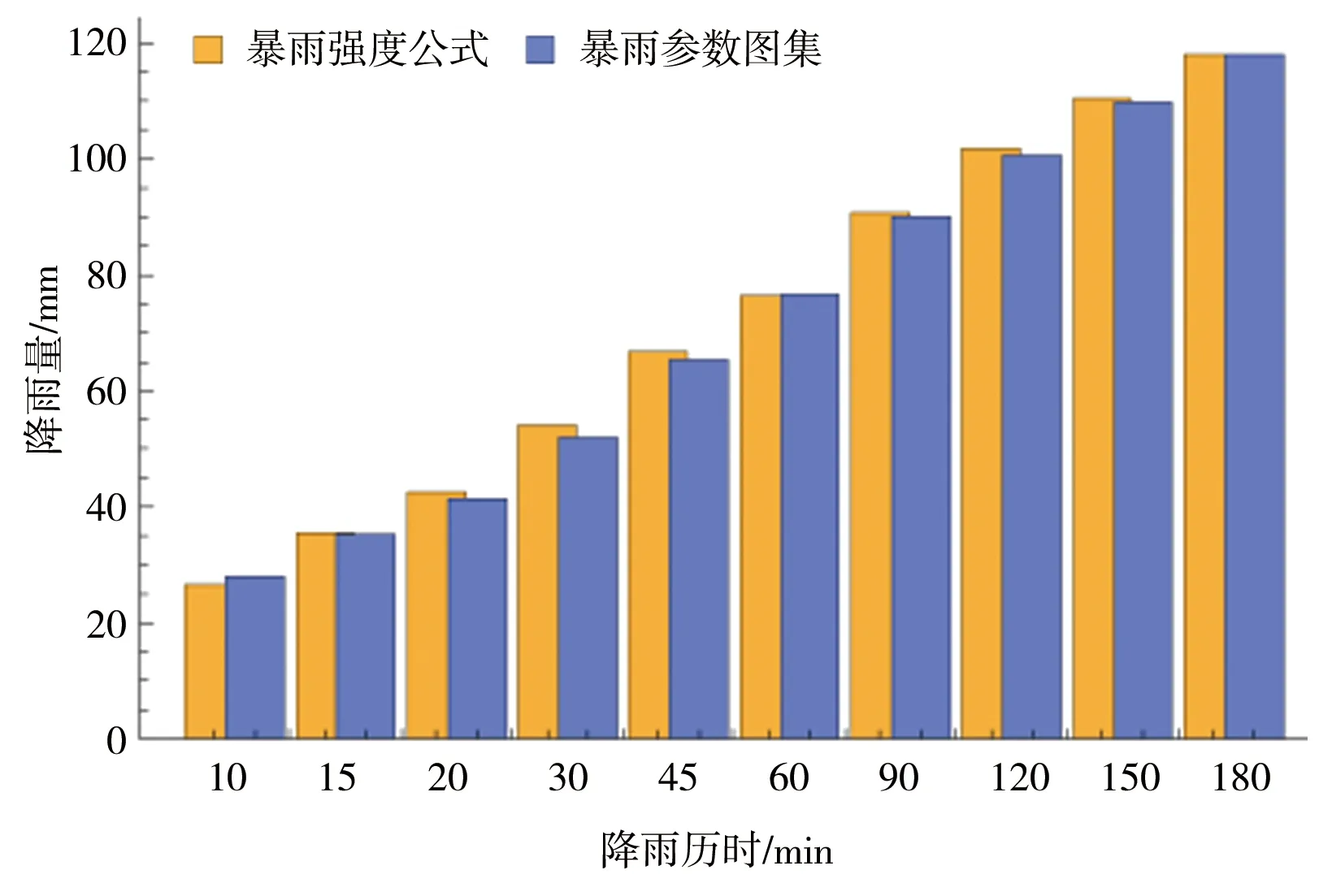
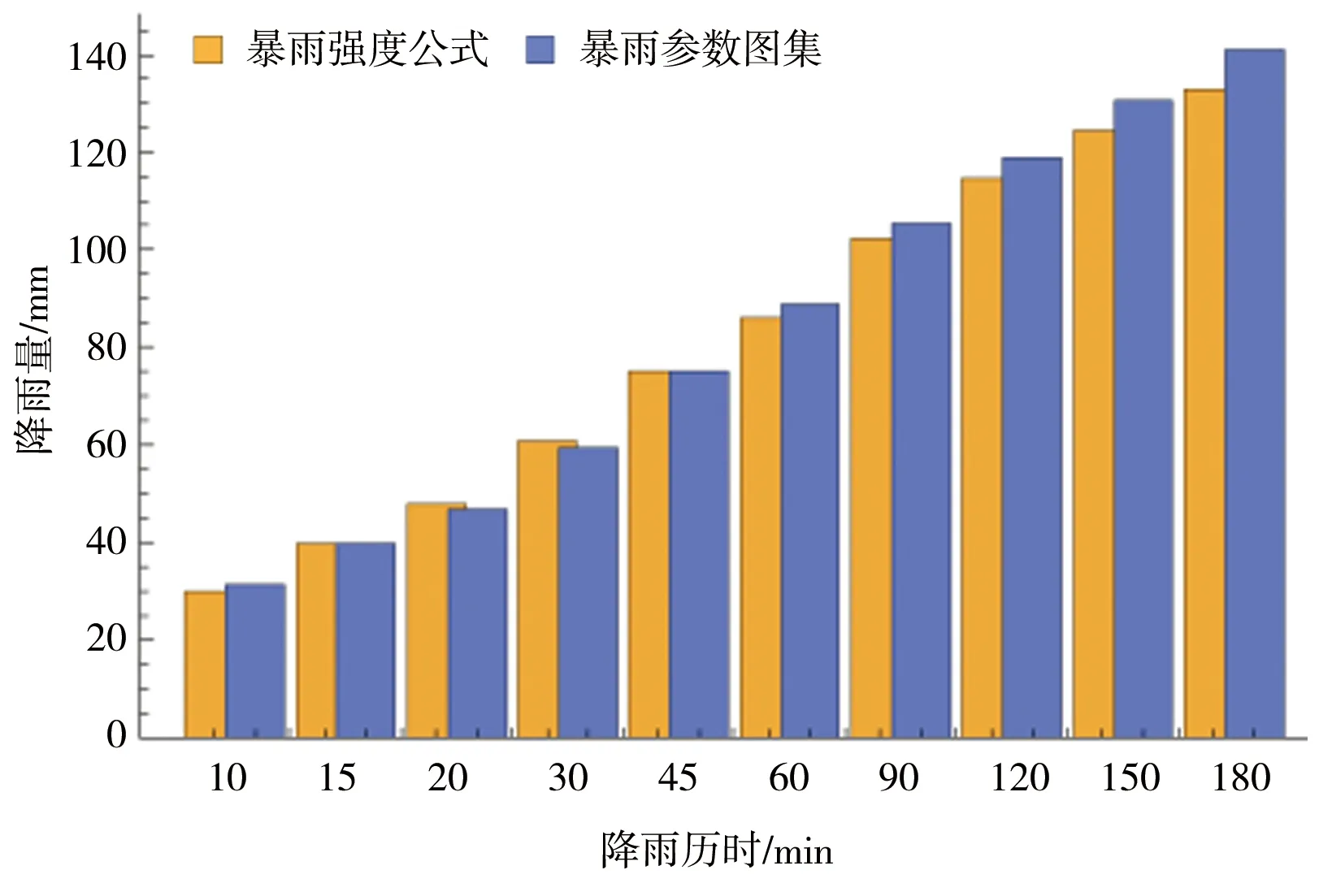
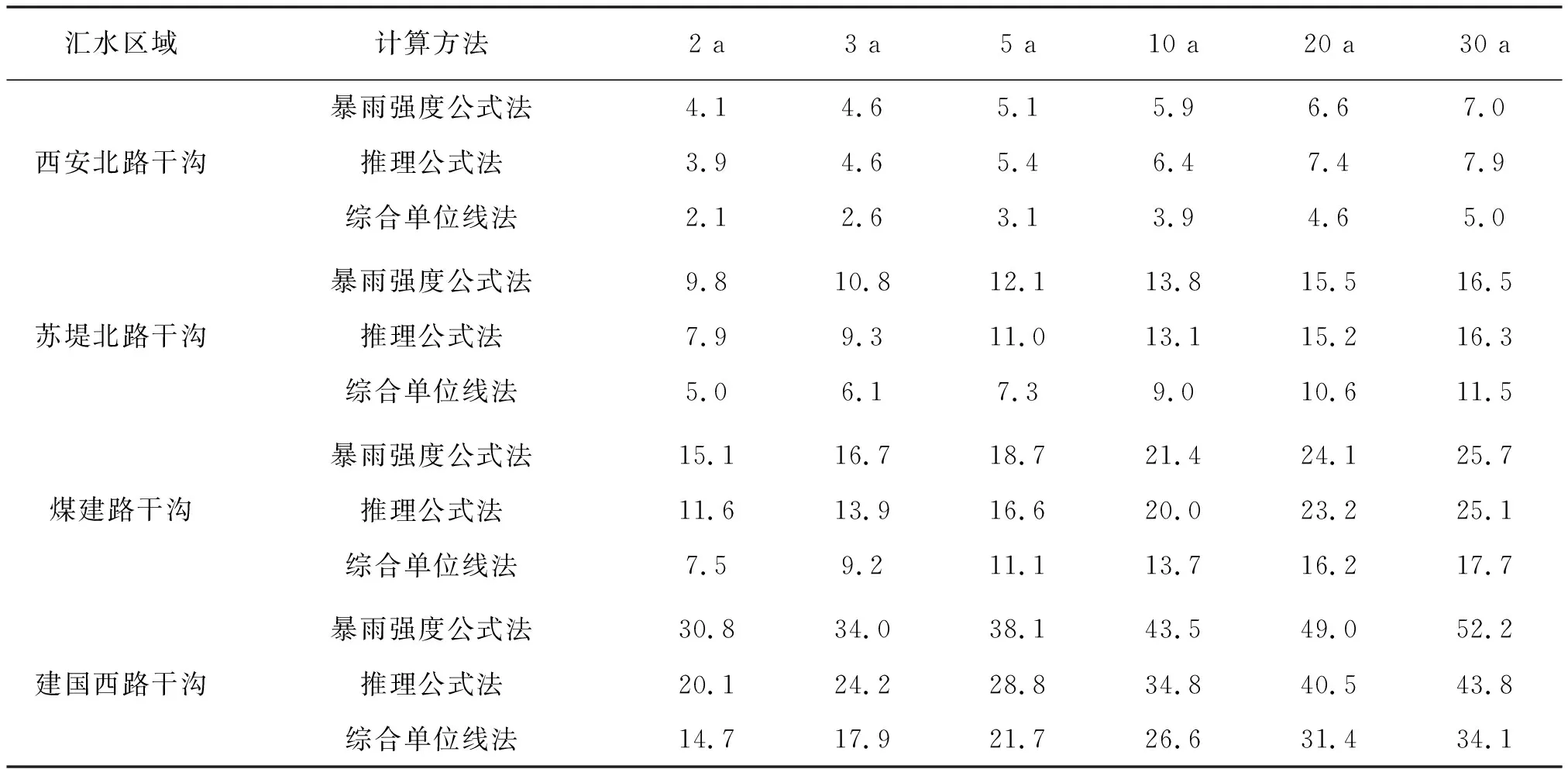
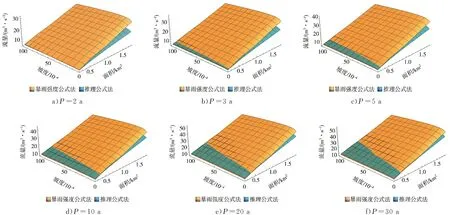
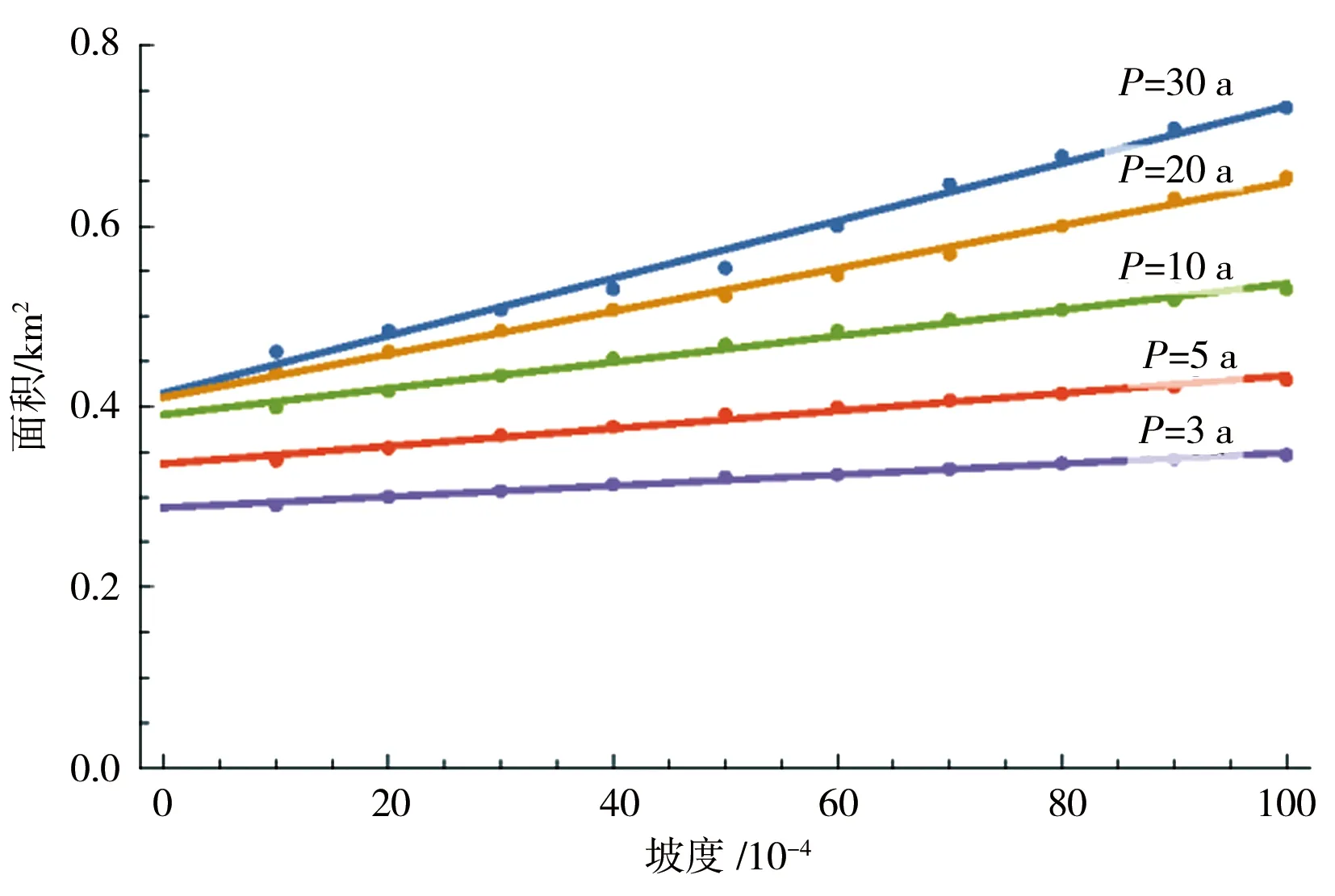
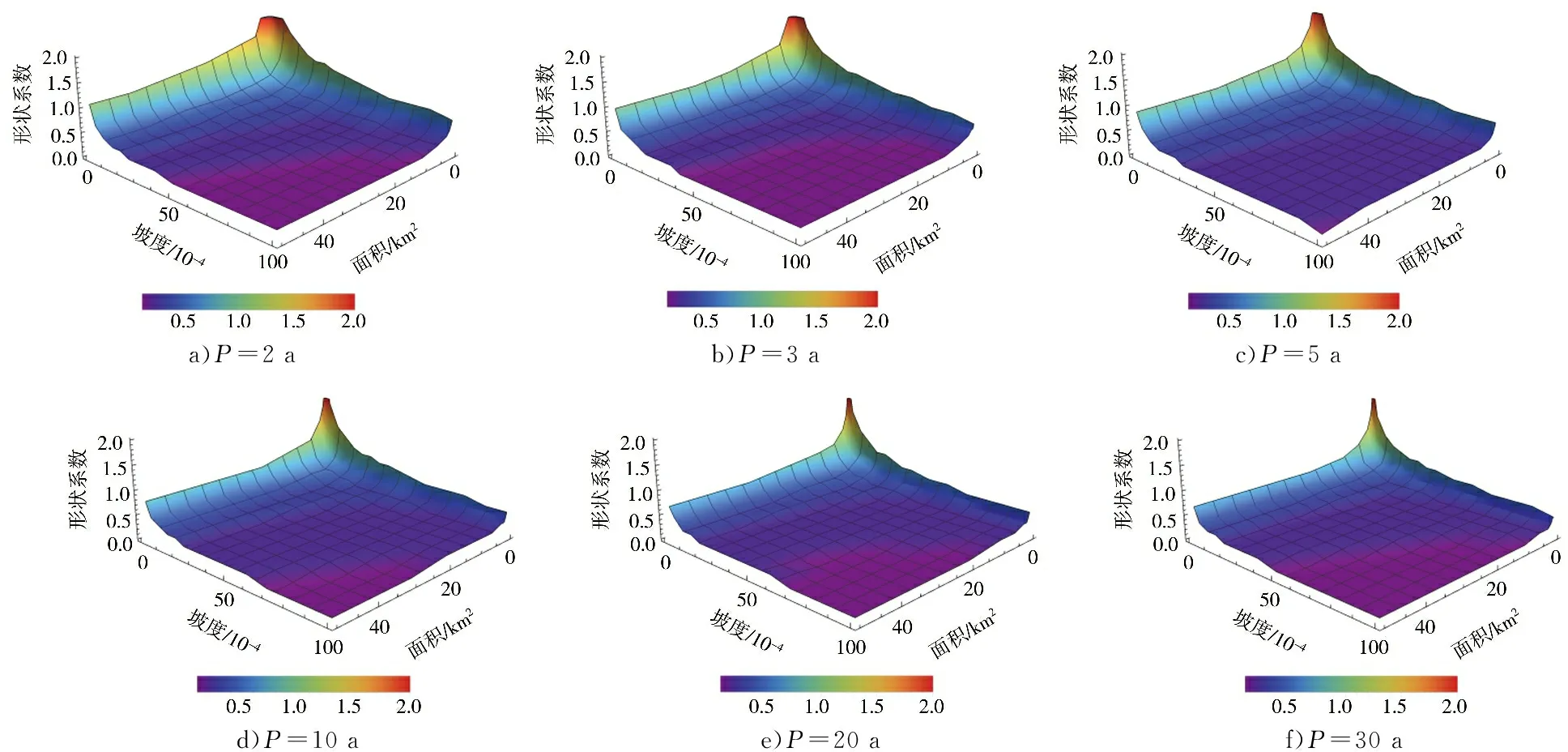
当10 min Ht,P=H1,P×t1-n1,P (4) n1,P=1-1.2851×lg(H1,P/H0.1667,P) (5) 当60 min Ht,P=H1,P×t1-n2,P (6) n2,P=1-1.2851×lg(H6,P/H1,P) (7) 式中n1,P、n2,P——10~60 min、60 min~ 6 h的某一设计重现期下的暴雨递减指数;H0.1667,P、H1,P、H6,P——10 min、60 min、6 h的某一设计重现期下的设计点暴雨量,mm。 暴雨强度公式和暴雨图集计算的设计暴雨量见图2。通过对比2种方法计算的设计暴雨量发现,当设计重现期小于等于5 a时,暴雨图集计算的各降雨历时的设计暴雨量一般小于暴雨强度公式;当设计重现期大于等于10 a时,暴雨图集计算的各降雨历时的设计暴雨量接近或大于暴雨强度公式。 a)P=2 a b)P=3 a c)P=5 a图2 设计点暴雨量对比 d)P=10 a e)P=20 a 分析其原因,因工程实践对重现期的要求不同,在满足点群趋势下,频率分析适线侧重考虑的范围就会有所差异:城市市政排水设计多考虑的是小重现期(一般2~20 a)短历时降雨量,防涝系统规划设计则会多考虑高重现期(20~100 a)长历时的雨量值[14]。高琳等[15]根据广州市中心城区连续52 a的实测年最大值样本系列,进行皮尔逊Ⅲ型分布曲线下短历时和长历时暴雨强度公式的频率适线分析,得出长历时适线在高重现期下斜率比短历时适线斜率大些,而在低重现期部分长历时适线斜率小于短历时适线。 由于市政排水管网汇水面积小,比如本文研究的4个汇水区域面积均小于2 km2,因此设计暴雨点面折算关系K值全部取1。 暴雨强度公式法、推理公式法汇流时间分别由公式计算,综合单位线法,设计降雨历时采用24 h降雨[16]。暴雨强度公式法和江苏省暴雨图集中推理公式法、综合单位线法,其差别除了公式推导假定条件的不同之外,还在于扣损方法和汇流时间计算方法不同[17]。 1.4.1扣损 用暴雨强度公式法计算设计净雨时,以综合径流系数反映暴雨扣损量,本文的4个汇水区域均位于老城区,建筑密集,综合径流系数ψ取0.60。用综合单位线法计算设计净雨时,按照《江苏省暴雨洪水图集(1984)》中方法,采用初损后损法,其中最大24 h净雨计算中,只扣后损,后损采用1 mm/h[18]。用推理公式法计算设计净雨时,按照《江苏省暴雨洪水图集(1984)》中方法,损失参数与后损率一致,使用时采用1 mm/h扣除[18]。 1.4.2汇流时间 汇流时间对运用暴雨强度公式法和推理公式法计算市政排水设计流量的影响比较大。汇流参数(m),相当于单位流量和比降为1的流域汇流速度,是推理公式法的核心[19]。确定汇流参数后就可以计算汇流时间(τ)。 暴雨强度公式法,是推理公式法应用在市政排水计算上的一个特例。暴雨强度公式采用极限强度理论,即当降雨历时(t)等于τ时,排水管道的设计流量最大。因此,暴雨强度公式中的降雨历时本质上反映的是汇流时间。 江苏省推理公式法,在参数综合时简化了汇流时间的计算,汇流时间只是汇水面积和平均坡度的函数,不体现流域长度(流域形状系数)的影响。而一般性的推理公式法,关于汇流参数和计算汇流时间的计算,有流域长度(流域形状系数)的影响因素在里面。《江苏省暴雨洪水图集(1984)》中的推理公式法计算汇流时间如下: τ=1.35×θ0.34 (8) θ=F/J1/3 (9) 式中τ——汇流时间,h;J——汇水区域平均坡度,;F——汇水面积,km2,下同。 综合单位线法,二参数m1、m2与汇水区域特征参数(汇水面积、平均坡度)联合,建立综合单位线的经验公式。根据《江苏省暴雨洪水图集》,参数m2比较稳定,山丘区、山丘平原混合区的m2值概化为1/3,经过地区综合后的苏北山丘区的m1值为: m1=2.4×(F/J)0.28 (10) 暴雨强度公式法计算市政排水设计流量的公式为[20]: QS=ψ×q×F (11) q=16.7i (12) 式中QS——设计流量,m3/s;ψ——综合径流系数,0.60;q——暴雨强度,m3/(km2·s);i——暴雨强度,mm/min;16.7——单位换算系数。 推理公式法计算市政排水设计流量的公式为[12,18]: QS=0.278×(A/τn-f)×F (13) 式中QS——设计流量,m3/s;0.278——单位换算系数;A——设计暴雨雨力,mm/h;τ——汇流时间,h;n——暴雨递减指数;f——平均损失参数,mm/h。 综合单位线法计算市政排水设计流量的方法为[12,18]:根据参数m1、m2及江苏省最大24 h设计暴雨雨型分配表,查时段单位线过程,用净雨过程卷积得设计流量。 暴雨强度公式法以设计重现期5 a为基准计算设计流量,设计重现期小于5 a的为校核流量,设计重现期大于5 a的为合理外推得到的流量。推理公式法和综合单位线法计算时,排水干管长度相当于流域主河槽长度,排水干管平均坡度相当于流域主河槽平均坡度。3种方法的计算结果见表3。 表3 不同方法下的设计流量对比 单位:m3/s 由表3可以观察到以下趋势:①当设计重现期较小时,暴雨强度公式法设计流量大于其他2种方法,汇水面积越大,差异越明显;②随着设计重现期的增大,其他2种方法设计流量增加率比暴雨强度公式法大,综合单位线法增加率最大,推理公式法次之,暴雨强度公式法最小;③从某一重现期开始,推理公式法设计流量大于暴雨强度公式法,但随着汇水面积的增加,推理公式法设计流量大于暴雨强度公式法所需要的重现期也在增大;④当汇水面积小于2 km2时,虽然综合单位线法设计流量增加率最大,但是始终小于推理公式法和暴雨强度公式法。 分析不同方法计算结果变化趋势的原因:①当设计重现期较小时,市政排水需要将地面雨水及时排除,随着汇水面积的增加,暴雨强度公式法中的面积叠加效应明显,因而汇水面积越大,暴雨强度公式法设计流量越大;②随着设计重现期的增大,暴雨图集计算的设计暴雨量比暴雨强度公式增加得多,因而暴雨图集2种方法设计流量增加率大于暴雨强度公式法。 上述工程实例中的4个汇水区域,下垫面条件即汇水面积、平均坡度、流域形状、地面种类是一定的,计算的设计流量是特定下垫面条件的结果,其中的主要影响因素是汇水面积和平均坡度。为了使计算方法的研究更具有普遍性,需要进一步讨论汇水面积、平均坡度二维组合条件下的设计流量的变化规律。 在汇水面积0.25~2.00 km2、坡度2~100范围内,分别运用暴雨强度公式法、推理公式法、综合单位线法计算设计流量,考察设计流量在汇水面积、平均坡度二维组合条件下的变化规律,并将3种方法的设计流量两两比较,见图3—5。 图3 暴雨强度公式法和推理公式法计算结果对比(<2 km2) 图4 暴雨强度公式法和综合单位线法计算结果对比(<2 km2) 续图4 暴雨强度公式法和综合单位线法计算结果对比(<2 km2) 图5 推理公式法和综合单位线法计算结果对比(<2 km2) 由图3可知,在汇水面积0.25~2.00 km2、坡度2~100范围内,随着设计重现期的增大,推理公式法设计流量逐步大于暴雨强度公式法,汇水面积越小越容易发生,这与表3观察到的趋势一致。此外,由于加入坡度变量,得以知道坡度的变化对暴雨强度公式法和推理公式法设计流量的影响,即在相同的设计重现期、汇水面积条件下,随着坡度的增大,推理公式法设计流量增加率大于暴雨强度公式法。 由图4可知,在汇水面积0.25~2.00 km2、坡度2~100范围内,暴雨强度公式法设计流量始终大于综合单位线法,并且两者之间不存在固定的对应关系。对比暴雨强度公式法和综合单位线法,市政排水和水利排涝之间的衔接标准随汇水面积、坡度变化而变化。通过分析计算,当汇水面积一定时,坡度越大,与市政排水标准对应的排涝重现期越小;当坡度一定时,汇水面积越大,与市政排水标准对应的排涝重现期越大。因此,有关文献通过计算洪峰流量得出的市政排水和水利排涝之间的衔接标准,只是一定汇水面积、坡度条件下的特例。 由图5可知,在汇水面积0.25~2.00 km2、坡度2~100范围内,推理公式法设计流量始终大于综合单位线法。对比推理公式法和综合单位线法,在计算汇水面积小于2 km2的特小流域洪峰流量时,推理公式法计算结果偏大,综合单位线法计算结果偏小,两者的设计流量没有交界线。 根据上述推理公式法和综合单位线法的对比,将汇水面积由2 km2增加到50 km2,在汇水面积0.25~50.00 km2、坡度2~100范围内对推理公式法和综合单位线法进行对比分析,见图6。由图6可知,在汇水面积0.25~50.00 km2、坡度2~100范围内,随着汇水面积、坡度的增大,综合单位线法设计流量逐步大于推理公式法,这种变化趋势几乎和设计重现期没有关系。 图6 推理公式法和综合单位线法计算结果对比(<50 km2) 在图3中,暴雨强度公式法和推理公式法的设计流量出现交界线,交界线以上,推理公式法设计流量小于暴雨强度公式法;交界线以下,推理公式法设计流量大于暴雨强度公式法。交界线上的面积和坡度为正比关系,交界线随设计重现期的变化而变化。暴雨强度公式法和推理公式法交界线上面积和坡度的关系(<2 km2)见图7。 图7 暴雨强度公式法和推理公式法交界线 在图6中,推理公式法和综合单位线法的设计流量出现交界线,交界线以上,综合单位线法设计流量大于推理公式法;交界线以下,综合单位线法设计流量小于推理公式法。交界线上的面积和坡度为反比关系,交界线几乎不随设计重现期的变化而变化。推理公式法和综合单位线法交界线上面积和坡度的关系(<50 km2)见图8。 图8 推理公式法和综合单位线法交界线 根据在汇水面积0.25~50.00 km2、坡度2~100范围内江苏省推理公式法设计流量的计算结果,反求相同设计流量下一般性推理公式法的形状系数,计算结果见图9。由图9可知,在一定设计重现期下,反求得到的形状系数随汇水面积、坡度的减小而增大;当设计重现期变化时,反求得到的形状系数整体随设计重现期的增大而减小。这说明江苏省推理公式法的地区综合,是全面的综合,不仅包括流域形状,还包括汇水面积、坡度以及重现期。计算中还发现,反求得到的形状系数随坡度变化的灵敏度比随面积变化高。 图9 形状系数的变化 通过讨论分析,暴雨强度公式法、推理公式法、综合单位线法设计流量在汇水面积、平均坡度二维组合条件下呈现出一定的变化规律。根据本次研究结果,对于汇水面积小于2 km2的市政排水:①暴雨强度公式法、推理公式法设计流量始终大于综合单位线法;②暴雨强度公式法和推理公式法设计流量有交界线,交界线随设计重现期的变化而变化;③暴雨强度公式法和综合单位线法设计流量不存在固定的对应关系,市政排水和水利排涝之间的衔接标准随汇水面积、坡度变化而变化。对于汇水面积小于50 km2的特小流域,推理公式法和综合单位线法设计流量有交界线,交界线几乎不随设计重现期的变化而变化。 对于市政排水设计流量,暴雨强度公式法、推理公式法的计算结果可以相互校核。对于市政排水和水利排涝之间的关系,暴雨强度公式法、综合单位线法的计算结果可以为标准衔接提供参考。总之,市政排水和水利排涝设计流量之间的标准衔接关系是个变量,而自变量是汇水面积和平均坡度,同时流域形状的不同会造成标准衔接关系发生波动。要达到两者之间的全面衔接,除了设计流量的衔接以外,尚需考虑水位、调蓄能力、排水时间等因素。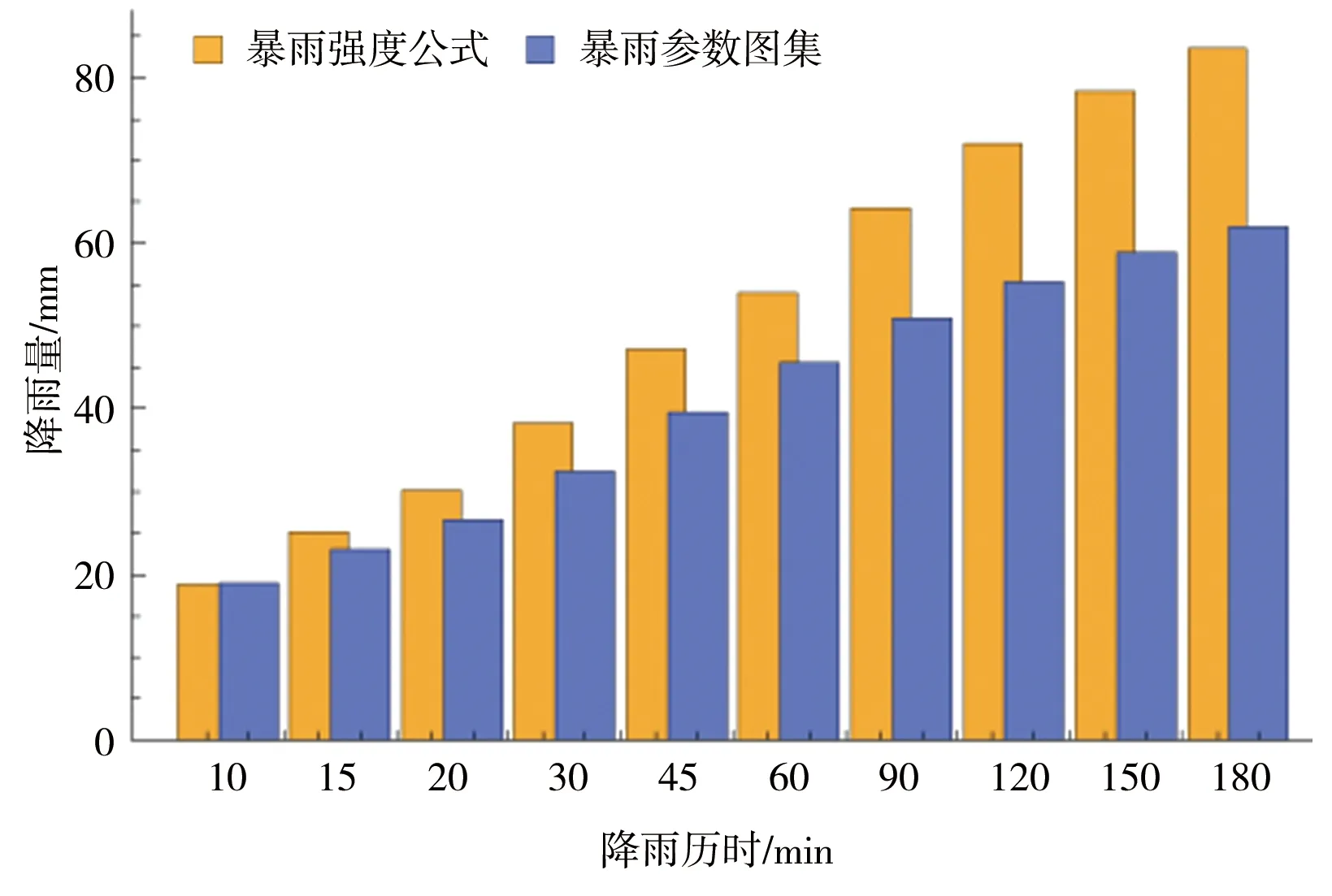
1.3 暴雨点面关系
1.4 产流、汇流分析
1.5 设计流量计算
2 讨论与分析
2.1 设计流量的变化

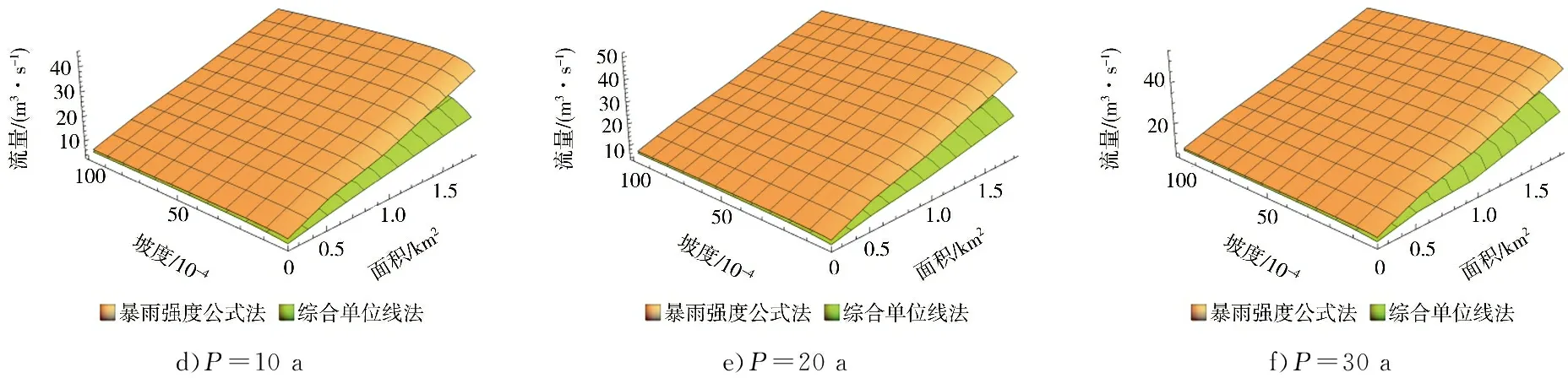
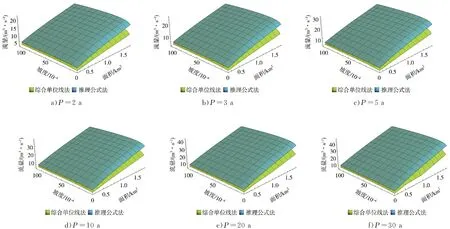
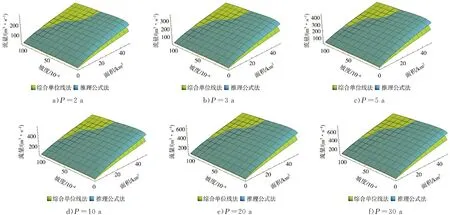
2.2 交界线的变化
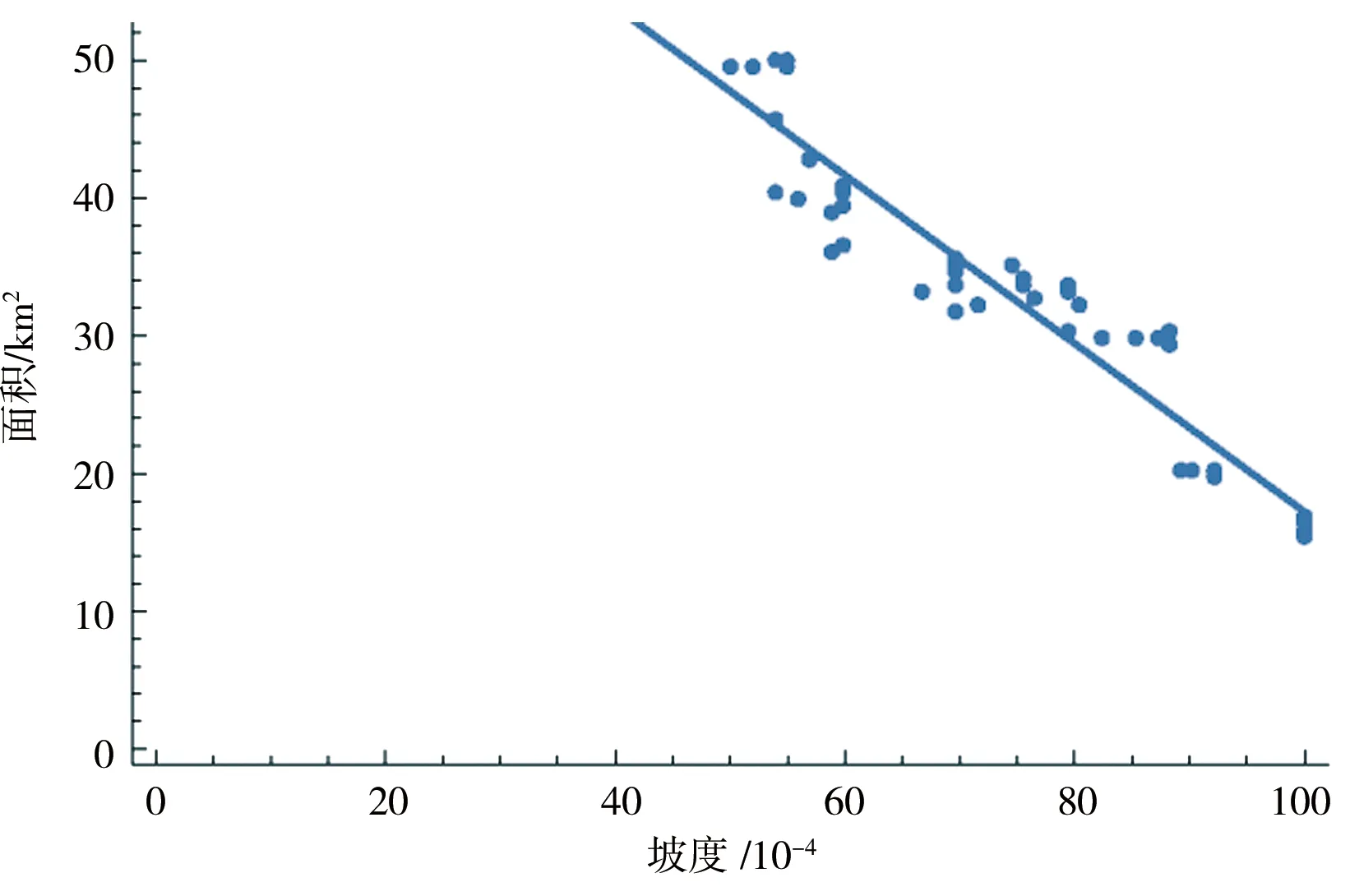
2.3 形状系数的变化
3 结论

