基于统计降尺度的东江流域未来气候预估

杜 懿

(中山大学地理科学与规划学院,广东 广州 510275)

近年来,在全球变暖的大背景下,区域气候的变化及影响引起了学界的广泛关注[1]。可靠的气候变化预估对于区域未来的发展规划、政策调整以及决策制定等具有重要意义[2]。全球气候模式(Global Climate Model,GCM)是现阶段用来进行气候变化模拟和预估研究的主要工具,通常对于大尺度范围内的平均气候状态有着较好的模拟效果[3-4]。然而,受多种因素限制,绝大多数GCM的水平空间分辨率都较低(>100 km),很难准确反映出小尺度或局地范围内的气候变化特征[5-6]。为扩展GCM在区域尺度上的应用,不同的降尺度方法先后被提出,且主要分为动力降尺度、统计降尺度以及动力与统计相结合的方法[7]。其中,统计降尺度方法由于计算量小、建模方便且扩展性高,得到了更为广泛的应用[8-9]。

目前,统计降尺度方法在国内外已经有了大量应用,代表性方法有BCSD (Bias Correction and Spatial Disaggregation)、BCCI (Bias Correction and Climate Imprint)、BCCA (Bias Correction Constructed Analogs)、SDSM (Statistical Downscaling Model)、ASD (Automated Statistical Downscaling Model)、CDFM (Cumulative Distribution Function Matching) 和Delta方法[10-14]。过往研究表明,SDSM模型在气温的降尺度模拟上通常表现优秀,而对于降水的模拟效果却不佳[15-18];CDFM和Delta方法属于偏差校正类模型,分别在分布形状修正和系统偏差消除上各具优势,目前常被用于降水的统计降尺度研究中[19-21]。需要注意的是,不同区域对于统计降尺度模型的响应可能存在较大差别,因此实际应用前通常要对模型的可靠性进行验证。

东江作为珠江流域的三大水系之一,长期承担着河源、惠州、东莞、广州、深圳和香港等地的供水需求,未来随着粤港澳大湾区的快速发展,其作为供水水源地的作用将得到持续提升[22]。全球变暖背景下,东江流域近些年来的气候特征也发生了较大变化[23-25],气候状态的改变将会直接影响到流域内的水资源量,因此,对东江流域开展未来气候预估研究具有重要的现实意义。基于此,本文以东江流域为研究区域,以流域内地面气象站点的观测资料和全球气候模式的输出数据为基础,分别对气温和降水进行统计降尺度模拟,并对未来不同排放情景下的流域气候变化做出预估。

1 数据来源与研究方法

1.1 研究区概况

东江流域地处113°52′～115°52′E,22°38′～25°14′N,总面积35 340 km2,高温多雨,属亚热带季风湿润气候区[26]。流域多年平均降水量约1 795 mm,多年平均蒸发量约1 200 mm,年均气温介于20～22 ℃,降水的年内分配差异较大,雨期主要集中在4—9月,降水量约占全年总量的80%以上[27]。东江流域内的气象站点及高程分布见图1。

1.2 数据来源

本研究共涉及到三类数据,分别为气象站点观测数据、大尺度环流因子再分析数据以及全球气候模式输出数据。东江流域内14个国家基本气象站点的逐日气温和降水观测数据来自国家气象科学数据中心(http://data.cma.cn/),时间跨度为1961—2014年。大尺度环流因子数据获取自NCEP再分析数据集(https://www.psl.noaa.gov/),该数据集提供了精度较高的全球范围内26个大气环流因子的长时间序列网格观测值,时间覆盖范围为1948—2018年,空间分辨率为2.5°×2.5°。

本文所选用的全球气候模式为第五次耦合模式比较计划中的CanESM2,数据来源于加拿大气候模式与分析中心(https://climate-scenarios.canada.ca/)。该模式的输出可划分为历史模拟期(1850—2005年)和未来预估期(2006—2100年),空间分辨率为2.8125°×2.8125°。同第五次耦合模式比较计划一致,该模式也包含有RCP2.6(低等浓度排放路径)、RCP4.5(中等浓度排放路径)和RCP8.5(高等浓度排放路径)等3种未来情景。

1.3 研究方法

1.3.1SDSM

SDSM是一种结合了多元线性回归和随机天气发生器的统计降尺度模型,具有交互性高、实用性强等特点[13]。模型的基本原理见式(1)—(3):

(1)

(2)

(3)

式中Ri——降水;Ti——温度;ωi——第i天发生降水的概率;Pij——第i天第j个大尺度预报因子;ei——模式误差;n——预报因子个数;α、β、γ——相关参数。

对于降水,要先模拟其发生概率(式1),再用随机天气发生器来模拟降水量(式2);对于温度,可直接模拟(式3)。

1.3.2CDFM

该法作为误差订正法中的代表,近年来在统计降尺度领域受到了越来越多的关注[28]。实际应用中,针对特定的气象要素,通常利用气候模式模拟值与气象站点观测值之间的累积分布函数差异来对气候模式的原始输出进行偏差校正进而达到降尺度目的。计算过程如下:

xm,cor=F0-1(Fm(xm))

(4)

式中xm,cor——校正后的气候模式模拟值;xm——气候模式的模拟值;Fm——气候模式模拟值的累积分布函数;F0-1——气象站点观测值的累积分布函数的逆函数。

1.3.3Delta方法

Delta方法是美国国家评价中心(http://www.nacc.usgcrp.gov/)所推荐应用的未来气候情景生成法[29]。该方法假设气候模式对于气候要素变化量的模拟要比对绝对值的模拟更加可靠,在对气候要素变化量的描述上,降水采用变化率,而温度采用变化量。气象站点未来降水和气温情景的计算公式见式(5)、(6):

(5)

Tf=To+(TGf-TGo)

(6)

式中:Pf、Tf——Delta方法重建的未来降水、气温序列;PGf、TGf——气候模式预估的未来降水、气温序列;PGo、TGo——气候模式在基准期内所模拟的多年平均降水、气温;Po、To——基准期内观测场的多年平均降水、气温。

1.3.4评价指标

本文使用平均绝对误差(Mean Absolute Error,MAE)、平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)、均方根误差(Root Mean Square Error,RMSE)以及皮尔逊相关系数(Pearson Correlation Coefficient,CC)等指标来评价模型的模拟效果。各指标的计算见式(7)—(10):

(7)

(8)

(9)

(10)

式中n——序列长度;yo、ym——实测值和模拟值;Cov——序列之间的协方差;Var——序列的方差。

其中,MAE、MAPE和RMSE的值越接近于0、CC的值越接近于1,表明模型的模拟能力越高。

2 结果与分析

在CanESM2全球气候模式的输出中,东江流域共覆盖有2个网格的范围,流域内编号为7和10的站点位于同一网格,其余站点则位于另一网格(图1)。为提高各站点的空间代表性,采用泰森多边形法来计算流域的面平均气候要素;在描述东江流域气候要素的空间分布特征时,使用Kriging方法进行插值。此外,使用SDSM模型对东江流域的气温情景进行降尺度处理,而对比使用CDFM和Delta方法来对东江流域的降水情景进行降尺度模拟。

2.1 降尺度模型构建

2.1.1气温

基于东江流域内14个气象站点的逐日观测数据和NCEP再分析资料,分别将各站点的预报量作为目标变量,将26个大气环流因子作为解释变量,通过建立逐步回归关系来筛选出各站点下各预报量的最佳组合预报因子,结果见表1。同时,为验证以上组合预报因子的选取是否合理,表2给出了各站点下各预报量的解释方差及标准误差。其中,解释方差表示提取到的因子对于目标变量的解释能力,最优值为1;标准误差用来表征模拟值与实测值间的偏差情况,最优值为0。

表1 预报因子筛选结果

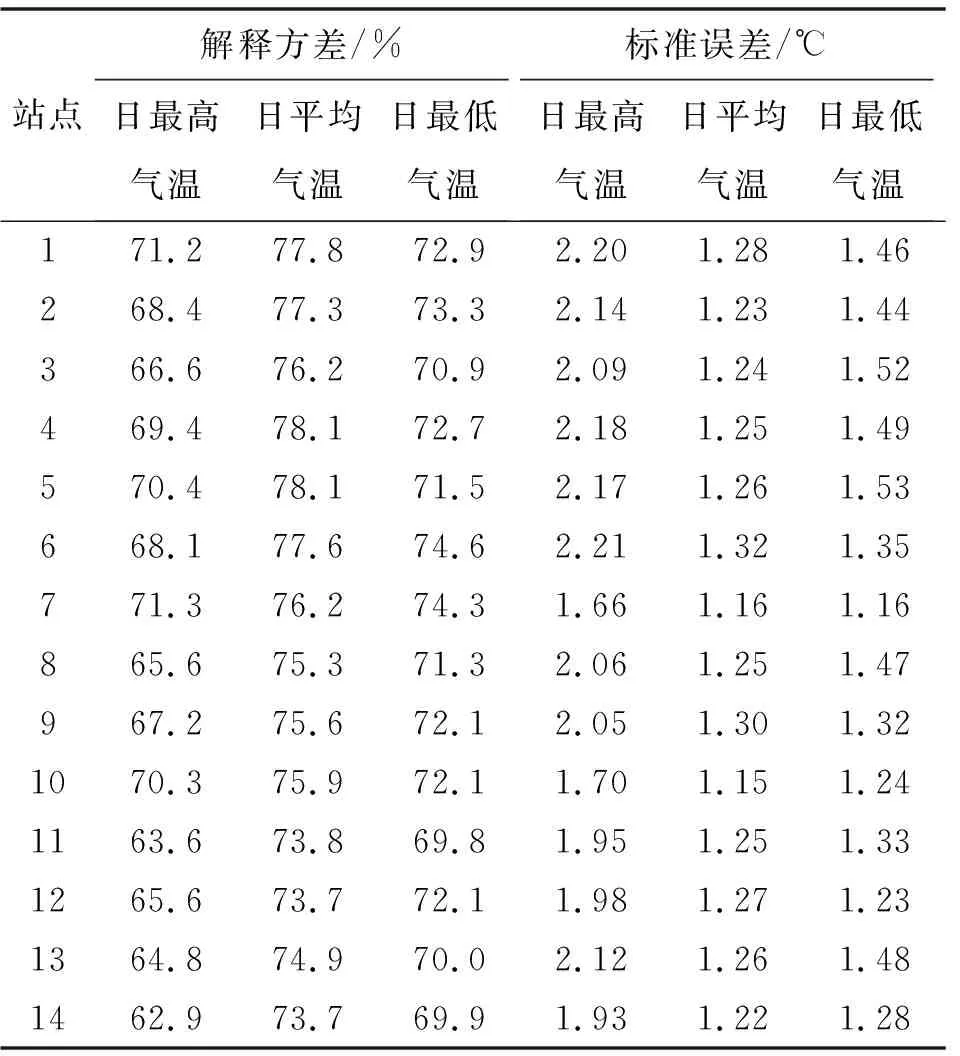
表2 各站点下各预报量的解释方差及标准误差

表2可见,对于日最高气温,各站点的解释方差为62.9%～71.3%,标准误差为1.66～2.21 ℃;对于日平均气温,各站点的解释方差为73.7%～78.1%,标准误差为1.15～1.32 ℃;对于日最低气温,各站点的解释方差为69.8%～74.6%,标准误差为1.16～1.53 ℃。整体来看,以上筛选出的组合预报因子对于东江流域内各站点气温的描述能力较好,平均解释方差达到了71.8%,平均标准误差为1.5 ℃。为检验SDSM模型的降尺度效果,分别选取1961—2000、2001—2005年作为模型的率定期和验证期,并综合使用MAE、RMSE和MAPE等指标来评价模型对于东江流域月平均日气温的模拟能力(表3)。

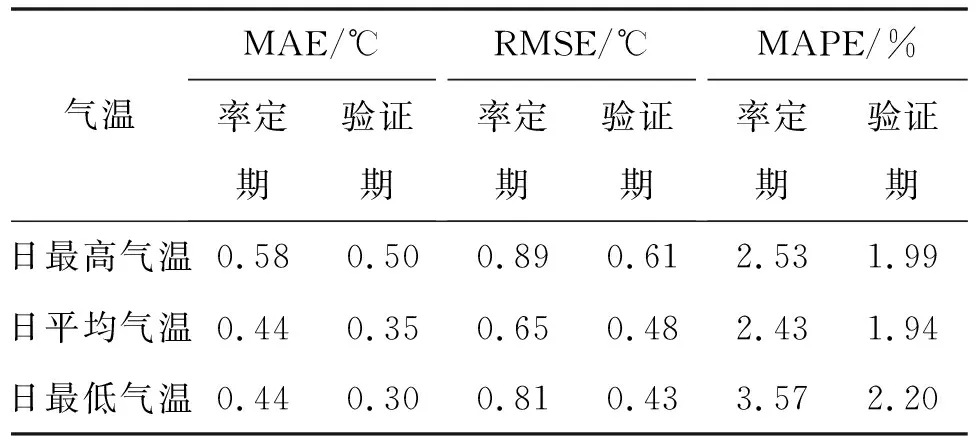
表3 基于SDSM模型的东江流域月平均日气温模拟效果检验

由表3可见,无论率定期还是验证期,SDSM模型的表现均十分优秀,各预报量的MAPE均低于3.6%,同时MAE和RMSE也都小于0.9 ℃。图2显示的是各预报量的模拟值与实测值在年内分配上的比较,二者十分接近,再次验证了模型的可靠性。

2.1.2降水

为构建出适合东江流域降水情景的统计降尺度模型,本文对比使用了CDFM和Delta方法。同样地,分别选取1961—2000、2001—2005年作为模型的率定期和验证期,并综合使用MAE、RMSE和CC等指标来评价2种模型对于东江流域月平均降水量的降尺度模拟效果。在应用CDFM时,采用两参数伽玛分布来对月降水量序列进行拟合,并使用极大似然法来估计分布函数中的相关参数。

表4显示的是CDFM和Delta方法2种统计降尺度模型对于东江流域月平均降水量的模拟效果。可以看出,无论率定期还是验证期,Delta方法相较于CDFM的模拟误差都更小且相关系数更高。图3描述的是CDFM和Delta方法对于东江流域各月多年平均降水量的模拟结果,明显可见,Delta方法的模拟值要更接近于实测值。综上,本文选用Delta方法来对东江流域的未来降水情景进行降尺度处理。

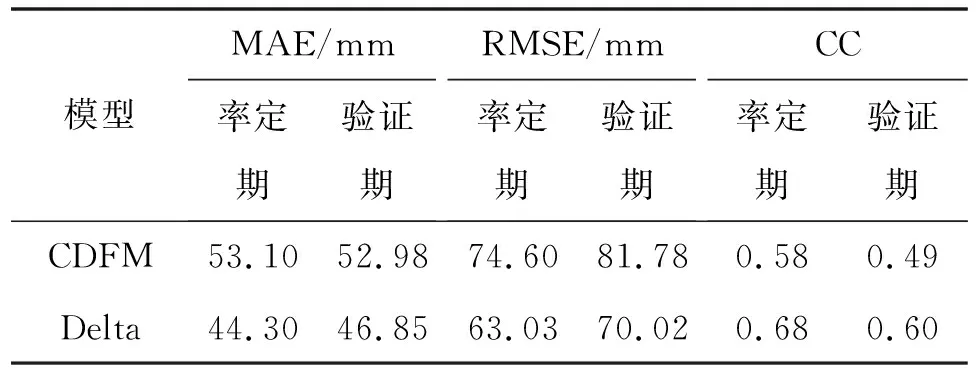
表4 基于CDFM和Delta方法的东江流域月平均降水量模拟效果检验

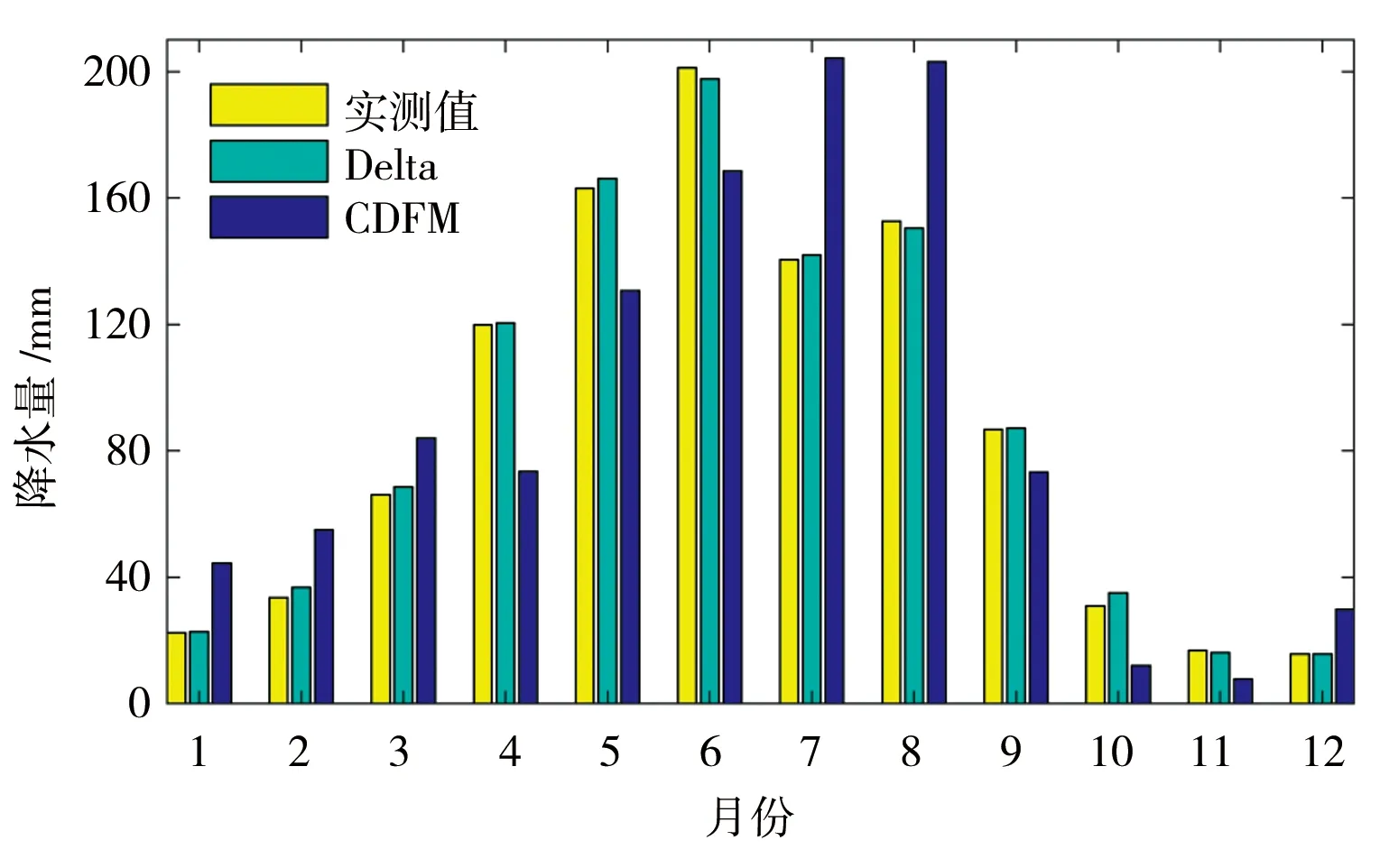
图3 2种统计降尺度模型对于各月多年平均降水量的模拟效果对比

2.2 未来气候预估

利用构建好的模型分别对CanESM2模式在2021—2100年的气温和降水输出进行降尺度处理,得到RCP2.6、RCP4.5和RCP8.5情景下东江流域14个气象站点的未来气温和降水序列。以1961—2005年为基准期,选取未来近期(2021—2050年)、未来中期(2051—2080年)和未来远期(2081—2100年)3个时段来分析流域未来气温和降水的变化特征。

2.2.1气温

图4显示的是不同排放情景下未来东江流域逐年平均日气温的变化过程。可以看出,在RCP4.5和RCP8.5情景下,流域平均日最低、日平均和日最高气温均呈现出明显升高趋势。其中,日最低气温增速分别为0.15、0.38 ℃/10a,日平均气温增速分别为0.19、0.50 ℃/10a,日最高气温增速分别为0.20、0.52 ℃/10a。与基准期相比,在RCP4.5和RCP8.5情景下,东江流域未来远期内的多年平均日最低气温将分别升高2.26、3.65 ℃,多年平均日平均气温将分别升高2.70、4.69 ℃,多年平均日最高气温将分别升高2.79、4.95 ℃。总的来看,东江流域的日最高气温增速最快、增幅最大,这可能会加剧流域未来的极端高温事件。

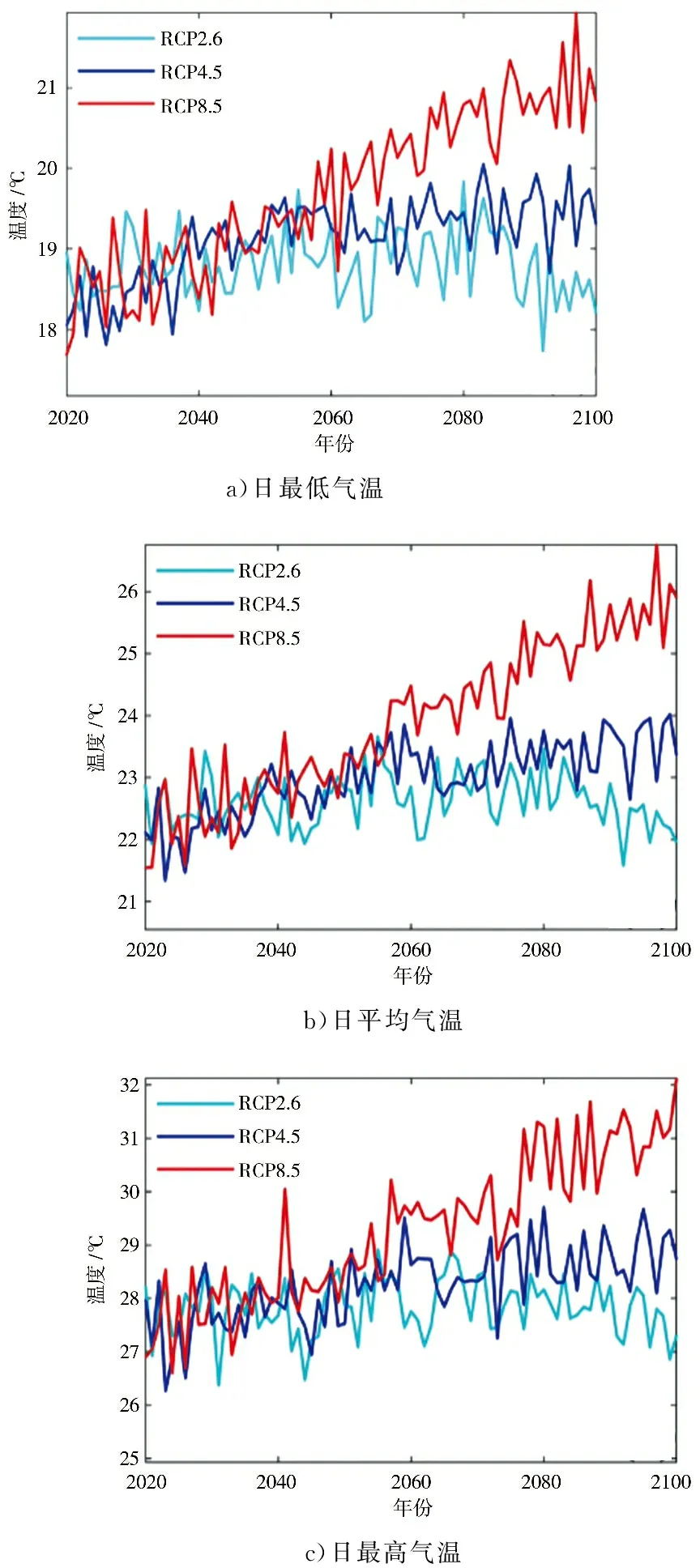
图4 不同情景下未来东江流域的逐年平均日气温变化过程

图5、表5分别显示的是未来远期内东江流域各月和各季的多年平均日气温相较于基准期的增幅情况。可以看出,各月的日最低气温、日平均气温和日最高气温相较于基准期均存在着不同程度的升高,且增幅从低到高依次为RCP2.6、RCP4.5和RCP8.5;未来远期内东江流域的日平均气温和日最高气温在秋季增加最为显著,而日最低气温则在冬季增幅最大,这表明流域未来的暖冬风险可能会有所增加。

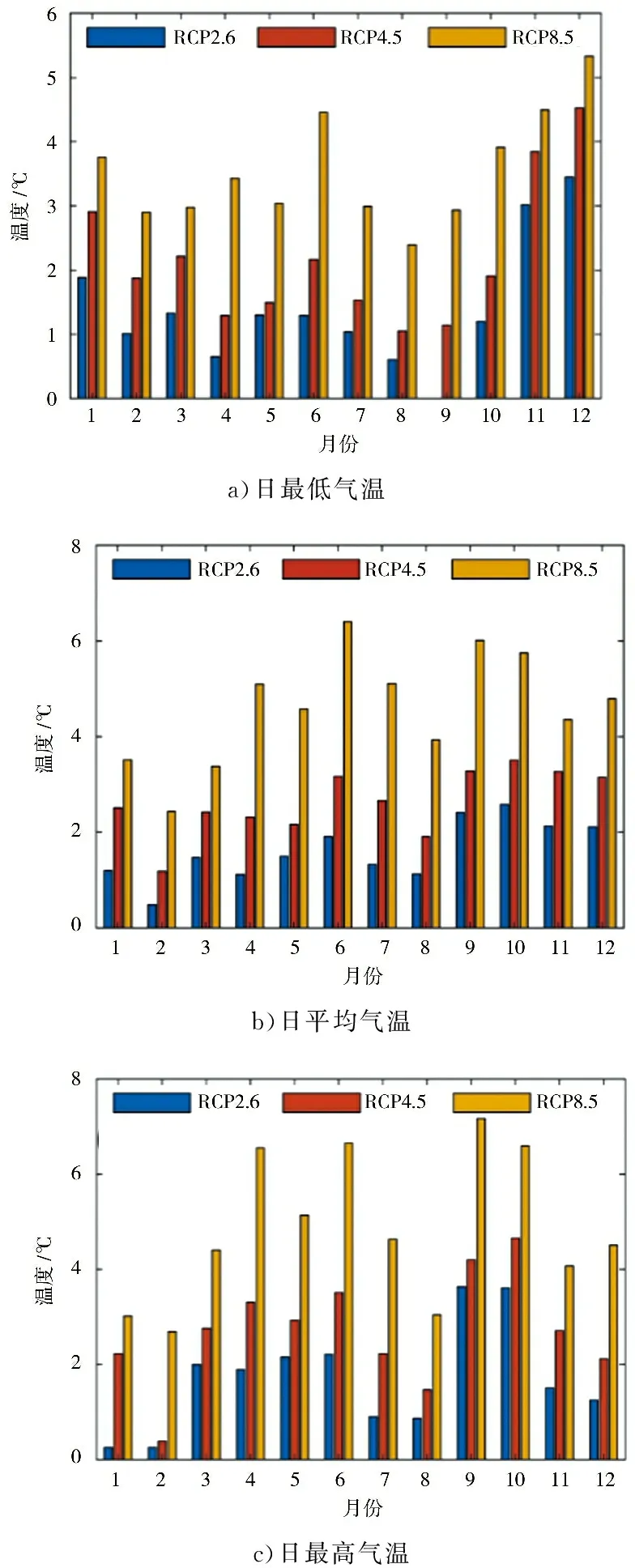
图5 未来远期内不同情景下东江流域内各月的多年平均日气温相较于基准期的增幅

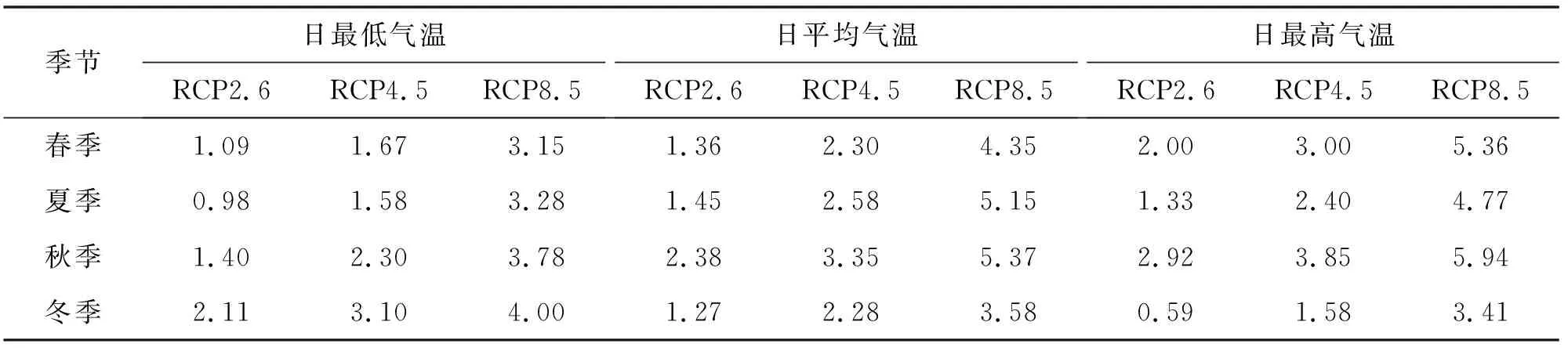
表5 未来远期内不同情景下各季节多年平均气温相较于基准期的增幅 单位:℃

图6描述的是未来远期内不同情景下东江流域多年平均日气温(日最低、最高和平均气温)相较于基准期增幅的空间分布情况。需要说明的是,在同一排放情景下,流域在未来远期的气温增幅要分别高于未来中期和未来近期,所以对该时段的分析最具有代表性。可以看出,未来时期不同排放情景下东江流域表现出全流域范围内的普遍升温;对于同一气温变量,随着温室气体排放浓度的增加(从RCP2.6到RCP4.5、RCP8.5),温度增幅也越来越大。从空间分布上来看,对于日最低气温,西南方向为增温高值区,东南方向为增温低值区;对于日平均气温,增温高值区在空间上呈不连续分布,主要集中在几个分散的区域;对于日最高气温,北部的增幅要明显高于南部,且空间连续性较强。

2.2.2降水

图7、表6分别显示的是未来不同情景下东江流域在2021—2100年的降水量时间序列及其统计特征值。可以看出,3种排放情景下的年降水量过程均呈现增加趋势,增速从高到低依次为RCP8.5(25.4 mm/10a)、RCP2.6(16.4 mm/10a)和RCP4.5(8.7 mm/10a)。年际变差方面,RCP8.5最大(200.5 mm),RCP4.5次之(184.4 mm),RCP2.6最小(170.5 mm)。此外,经计算,东江流域在基准期内的多年平均降水量为1 050 mm,未来时期在RCP2.6、RCP4.5和RCP8.5情景下的多年平均降水量将分别增加103.1、149.8和164.6 mm。

图7 不同情景下未来东江流域的年降水量变化过程

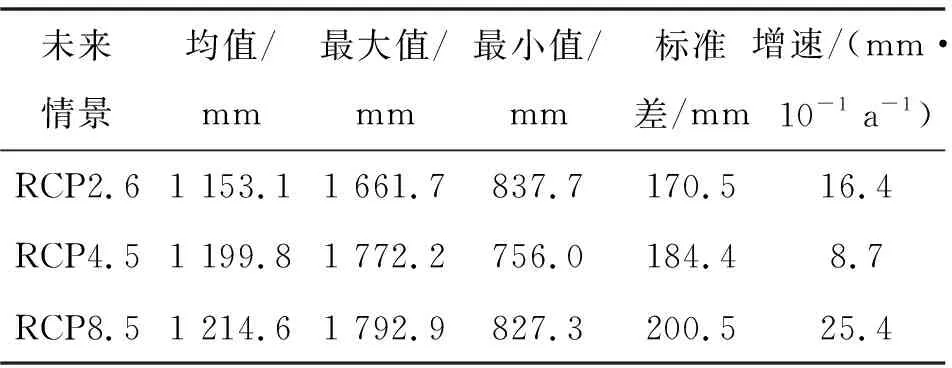
表6 不同情景下未来东江流域年降水量序列的统计特征值

图8、9分别显示的是未来不同时期内不同排放情景下东江流域的多年平均月、季尺度降水量变化过程。可以看出,未来不同时期内,3种排放情景下的月降水量较基准期均有所增加,且以6月份增加最为显著(图8);季节上,则以夏、秋两季的增加较为明显(图9)。综合来看,未来东江流域在汛期内所面临的暴雨洪灾风险可能会有所上升。

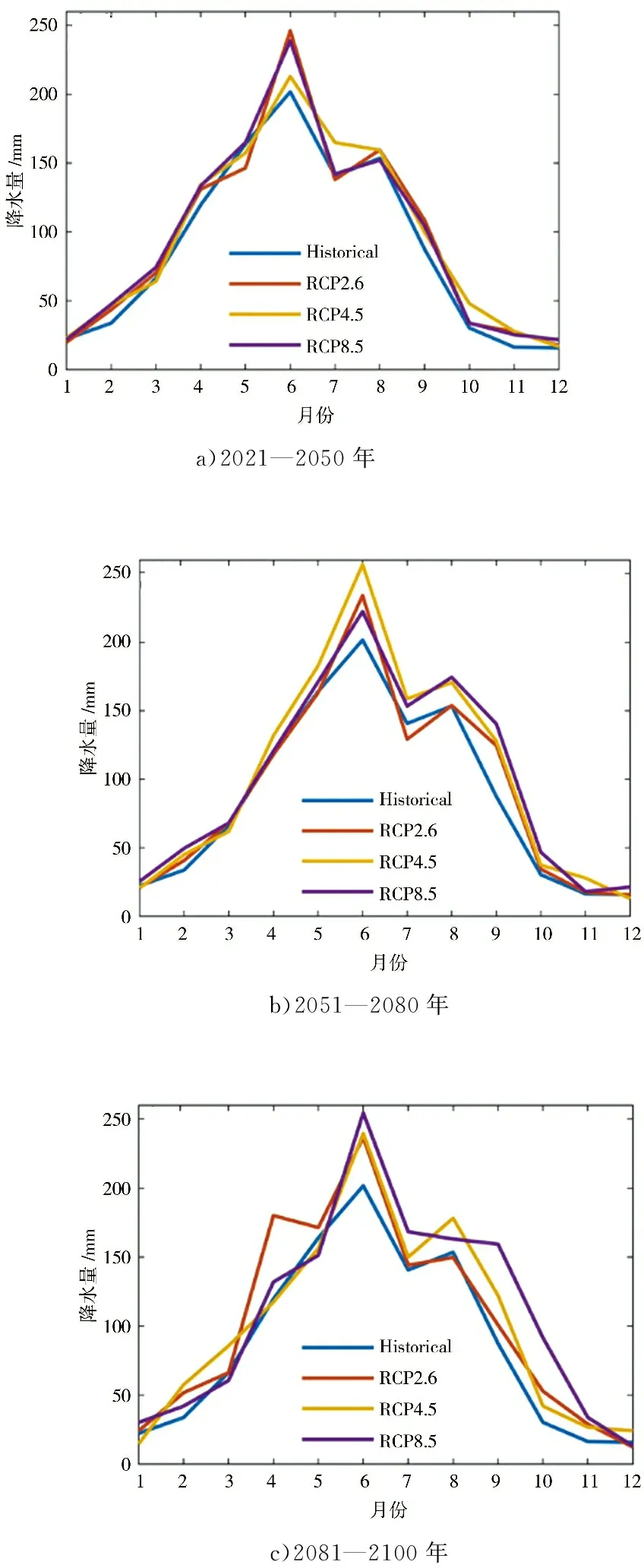
图8 未来不同时期内不同情景下东江流域各月份的多年平均降水量变化

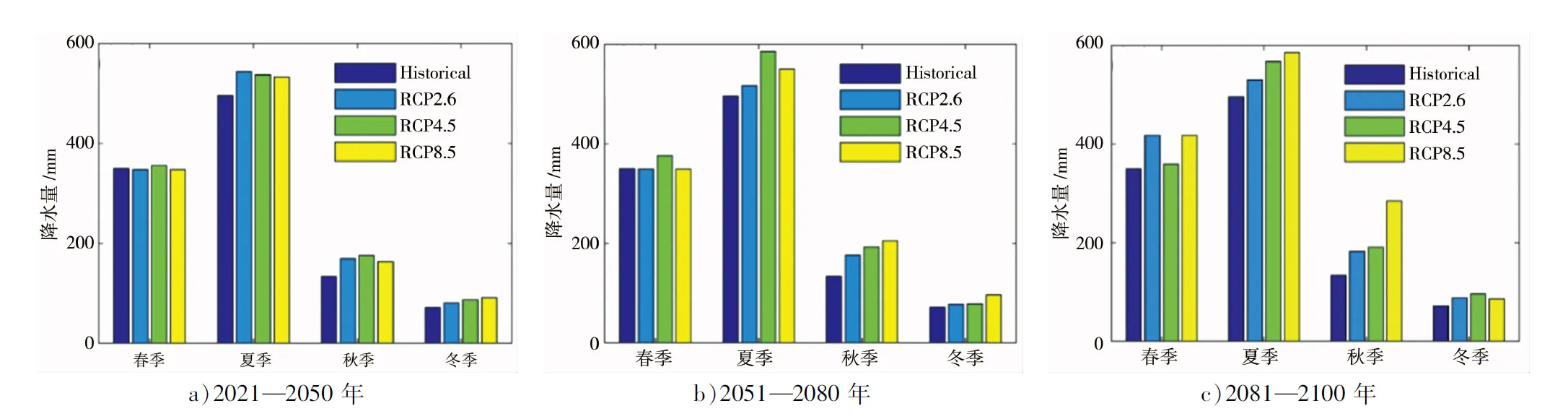
图9 未来不同时期内不同情景下东江流域各季节的多年平均降水量变化

图10描述的是未来不同时期内不同排放情景下东江流域多年平均降水量的空间分布情况。可以看出,在同一排放情景下,随着时间的推移,降水量在空间上呈现出逐渐增加的态势,且在RCP8.5情景下降水增加最为显著;同一时期内不同排放情景下,降水量的空间分布格局并未发生明显改变,这点与气温的变化有所不同,表明降水对于温室气体浓度变化的响应可能不如气温敏感。此外,虽然流域在未来时期的降水量呈现出增加趋势,但在不同时期内不同情景下的降水中心却较为稳定,虽然覆盖范围有所扩展但整体位置并未发生明显迁移,大体位于流域中部偏西的位置(蓝色阴影区域)。

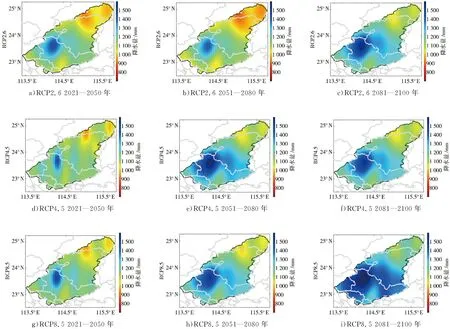
图10 未来不同时期内不同情景下的东江流域多年平均降水量空间分布

3 结论

以东江流域为研究区域,以流域内14个气象站点的逐日观测数据为基准值,使用多种统计降尺度方法分别对CanESM2全球气候模式的气温和降水输出进行了模拟,并对流域未来不同情景下的气候变化做出了预估。主要取得了以下研究成果。

a)经验证,SDSM模型和Delta方法分别对于东江流域的气温和降水有着较好的降尺度模拟效果,该结论可为今后东江流域气象因子的统计降尺度研究提供参考。

b)在RCP4.5和RCP8.5情景下,未来东江流域的日最低、日平均和日最高气温将持续升高,且同一排放情景下,日最高气温的增速最快;相较于基准期,流域在未来远期内的多年平均日最低气温将分别增加2.26、3.65 ℃、日平均气温将分别增加2.70、4.69 ℃、日最高气温将分别增加2.79、4.95 ℃。

c)未来不同排放情景下东江流域的年降水量均呈现出增加趋势,相较于基准期,多年平均降水量增幅从高到低依次为RCP8.5(164.6 mm)、RCP4.5(149.8 mm)和RCP2.6(103.1 mm);此外,随着时间的推移,降水在空间分布上也呈现增加态势,但不同时期内不同排放情景下的降水中心基本保持稳定。

通过对全球气候模式的输出进行空间降尺度处理,使得开展区域或局地尺度上的气候变化研究成为了可能[30]。然而,由于降尺度的本质是对气候模式输出的一种后处理,其过程不可避免地存在着不确定性,尤其是统计降尺度[31]。首先,统计降尺度模型的构建十分依赖于观测资料的获取,不同长度的观测资料所率定出来的模型可能差别较大,一般来说,数据跨度越长所建立起的统计关系就越可靠;其次,SDSM等基于多元回归的降尺度模型在构建过程中需要预先进行解释因子的选取,而如何准确高效地优选出这些因子尚未有统一的理论和方法;此外,针对不同的气象要素,统计降尺度模型的构建思路存在着较大差别,如对温度的降尺度处理多采用多元回归的方法,而对降水的处理则主要采用偏差校正的方法,这可能是因为降水具有更强的时空异质性。在本文中,SDSM模型被证实在气温的降尺度模拟上表现较好,这与过往研究基本一致[32-34];降水方面,Delta方法的表现要优于CDFM,但该结论可能并不具备普遍性,因为统计降尺度模型的表现往往依赖于气候模式的选取和研究区域的气候特征。需要强调的是,虽然CanESM2气候模式在研究区内有着较好的模拟能力,但单模式的预估结果存在着较大的不确定性,在今后的研究中,将尝试采用多模式集合平均的方法来进行区域气候的预估。