基于极化敏感阵列抗有源干扰的测向算法

沈千秋, 赵勇武, 夏新凡, 吴迎春, 奚 银

(上海无线电设备研究所, 上海 201109)

0 引言

在现代化电子战争中,为对抗反辐射导弹的“硬杀伤”,避免目标雷达受到干扰和攻击,防空反导系统多采用有源诱饵、雷达组网、间歇发射等各种对抗手段。其中有源诱饵因其高诱偏性能及低成本,成为对抗反辐射导弹最有效的手段之一。目前,美欧等军事列强的各类防空反导系统普遍配备了有源诱饵设备[1]。

被动雷达导引头是反辐射导弹的重要传感装置,通过对目标雷达电磁信号的截获和跟踪,引导反辐射导弹打击目标雷达,其性能直接影响导弹的作战性能。因为被动雷达导引头只能依靠接收辐射源辐射的电磁信号来测向,在面对功率相当且与目标雷达信号相似度很高的诱饵信号时,采用传统的比幅比相测角体制[2]获得的角度分辨能力有限,极易被诱偏[3-4]。空间谱估计测向体制[5]因其角度超分辨能力,可用于对抗有源诱饵诱偏。但传统的空间谱估计算法无法适应随机变化场景,也不能从测得的角度中分辨真实目标的角度。

本文基于传统的极化敏感阵列多重信号分类(multiple signal classification,MUSIC)[6]测向算法,提出一种适用于多目标辨别的测向算法。该算法主要采用极化滤波与斜投影算子[7-8],结合极化域-空域二维联合空间谱估计,实现对有源诱饵与目标雷达的角度分辨,同时根据目标雷达与诱饵的极化域特性差异,识别目标雷达,从而实现诱饵对抗。

1 应用场景

1.1 有源诱饵

有源诱饵可分成单点源诱饵、双点源诱饵及多点源诱饵等[9]。单点源诱饵干扰时需要目标雷达关机,以单一假目标干扰来诱偏反辐射导弹,极大可能导致单点源诱饵的消耗。虽然诱饵的成本相较于雷达的成本低一些,但是因为诱饵需要模仿雷达的信号特征,其结构依然较为复杂,成本也不低,因此其并不适合作为消耗品使用。另外,当单点源诱饵被消耗后,目标雷达或因面临多波次的反辐射导弹攻击而不再开机,雷达关机牺牲了其探测效能,也对作战不利。

双点源诱饵与多点源诱饵是最常用的有源诱饵干扰。双点源诱饵一般出于保护目标雷达的考虑,通过增加诱饵的功率,使得反辐射导弹偏向诱饵(假目标),达到保护目标雷达的目的。如果出于对诱饵回收的考虑,可使诱饵与雷达功率相同,这时对目标雷达的保护效能取决于两点源诱饵的间距。采用比幅比相体制测向的反辐射导弹一般会跟踪两点源诱饵的“能量质心”。若两点源诱饵距离过近,则反辐射导弹的杀伤半径可能威胁到目标雷达;若两点源诱饵距离过远,对于机动性强的反辐射导弹,在迫近两点源诱饵的飞行过程中,可能分辨出两点源诱饵,并直接命中其中一个干扰辐射源。

多点源诱饵布阵的方式与双点源诱饵诱偏类似。文献[1]指出,单点源诱饵与目标雷达构成双点源诱饵系统实施诱偏是不实用,且不安全的;双点源诱饵与目标雷达构成三点源诱饵系统实施诱偏比较实用,但是目标雷达仍不是最安全的;三点源诱饵与目标雷达构成的四点源诱饵系统诱偏效果较好,可使目标雷达的安全性大大提升。

就诱饵与目标雷达的距离而言,有源诱饵通常设置在被保护的目标雷达附近,距离一般为(300～1 000)m[1]。对有源诱饵的合理排布能极大地提升反辐射导弹的被动制导性能。就诱饵与目标雷达的信号功率而言,有源诱饵的功率一般低于目标雷达的主瓣功率,与雷达副瓣的功率相当。就诱饵与目标雷达的信号时序而言,有源诱饵的信号前沿一般超前于目标雷达信号前沿,后沿滞后于目标雷达信号后沿。就诱饵与目标雷达的信号特征而言,假设目标雷达为脉冲体制,那么诱饵信号在信号特征上与目标雷达的信号特征相同或相近,即脉冲宽度、脉冲重复周期均相同,载频相近。相似的信号特征是提高诱饵诱偏反辐射导弹几率的必要前提[9]。

1.2 极化MUSIC算法

极化 MUSIC 算法在传统的标量阵列MUSIC算法中增加了极化维信号处理。极化是电磁信号的固有属性,是除信号频率、幅度、相位、波形以外另一可以利用的有效参数。标量阵列仅能接收空域电磁信号的一个场分量的信息,其信号处理一般只能利用空域信号波前中所隐含的空间相位信息。标量阵的处理性能与阵列孔径大小以及信号波长有较大关系,对极化形式不同的信号的响应有时会出现异常。而极化敏感阵列具有敏感响应空间内的电磁信号极化信息的能力,能够获得电场、磁场的全部六维或部分维信息。基于极化敏感阵列[10-12]的MUSIC 算法,具有比标量阵列MUSIC 算法更低的克拉美罗下界(Cramer-Rao lower bound,CRB),因此具有更好的测向潜能[12]。基于极化敏感阵列的信号处理,可使得空间中信源的多维参数估计、信号检测等的性能得到更进一步的改善。利用感兴趣信号与干扰信号极化信息的差异,可对后者进行有效抑制,使得对感兴趣信号的估计更为准确。

2 算法原理

2.1 阵列接收信号模型

以极化敏感均匀圆阵的圆心为坐标原点o,所在平面为xoy平面,建立空间直角坐标系oxyz,如图1所示。假设有一远场信号s入射到由N个阵元组成的天线阵面,射线so与xoy平面的夹角定义为仰角φ,射线so在xoy平面的投影s′o与x轴正向的夹角定义为方位角θ。

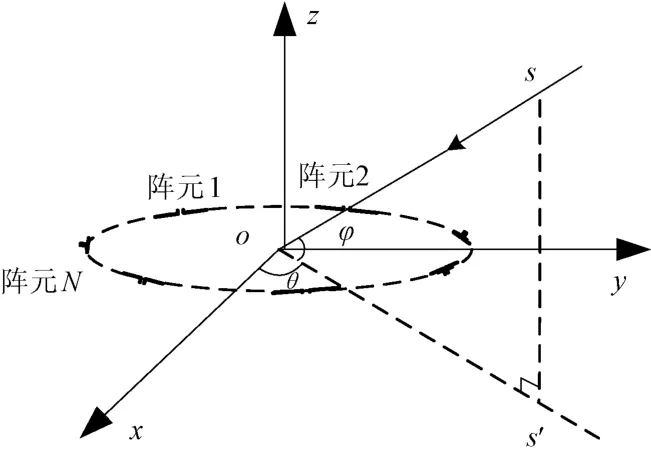
图1 空间参考坐标系

设有K个远场窄带完全极化电磁波信号,入射到由N个天线阵元构成的空间极化敏感阵列,其中第k(k=1,2,…,K)个入射信号的方位角及仰角为θk,φk、极化辅助角及相位差为γk,ηk。天线阵元在空间任意排列,设第n(n=1,2,…,N)个天线阵元的位置坐标矢量ln=[xn,yn,zn]T,其中xn,yn,zn为第n个天线阵元在oxyz坐标系中的坐标,T 为转置运算符。以原点o为参考点,第n个天线阵元与原点o间的波程差为该天线阵元的位置坐标矢量在信号入射方向上的投影,则第k个入射信号入射到第n个天线阵元与原点间的空间相移因子

式中:rk表示第k个入射信号在入射方向上投影的单位矢量;λk表示第k个入射信号的波长。

第n个天线阵元的极化敏感矢量

根据完全极化波电磁特征可知,第k个入射信号的极化域-空域导向矢量

则第k个入射信号的导向矢量

式中:Uk为第k个入射信号的空域相移因子矩阵;diag(·)为对角矩阵函数;B为极化敏感矩阵。

对于完全极化波,N×1维的阵列输出信号矢量

式中:A=[a1,…,ak,…,aK]为由阵列空域结构及阵元结构决定的阵列流形矩阵,其维度为N×K;S为入射信号矢量,其维度为K×1;N为阵列接收噪声矢量,其维度为N×1。

2.2 混叠信号前沿估计

假设由接收机接收到的混叠信号的前沿为X1,通常前沿段信号只包含1个信号,无需进行信源数估计。求X1的协方差矩阵,其中H 为共轭转置运算符,并对协方差矩阵进行特征分解。信号特征矢量所张成的子空间与阵列导向矢量a(θ,φ,γ,η)所张成的子空间是一致的。根据信号子空间与噪声子空间Un的正交性原理[13],取低秩空间为噪声子空间Un,此时显然有

构造谱函数

令a(θ,φ,γ,η)=D(θ,φ)h(γ,η),其 中D(θ,φ)为空域分量矩阵,h(γ,η)为极化域分量矩阵,则式(8)可改写为

式中:det(·)表示矩阵行列式运算;argmin(·)表示函数为最小值时自变量取值函数。

对式(8)进行谱峰搜索,得到的谱峰极大值所对应的方位角及仰角,即为入射信号的波达方向(direction of arrival,DOA)。同理可获取信号的极化参数估计。

由于直接进行θ,φ,γ,η四维搜索过程较为复杂,为降低复杂度并减少运算量,可直接进行秩亏二维谱峰搜索[14]。

在估计得到方位角与仰角之后,再进行极化参数估计。信号的极化参数γ,η可通过求解式(11)的优化问题得到。设J(θ,φ,γ,η)为目标函数,有

式中:‖·‖表示矩阵取模运算。

则可得到H(θ,φ)和DH(θ,φ)D（θ,φ）的广义特征矢量[14]

2.3 混叠信号极化滤波

取混叠信号前沿段X1234,求取协方差矩阵,并对协方差矩阵进行特征分解。一般认为前沿段信号为诱饵信号,且假设各诱饵的极化参数相同。设信号入射的方向为(θ,φ),根据混叠信号前沿段估计的诱饵信号极化参数为(γ1,η1)。根据信号子空间与噪声子空间Un的正交性,此时显然有

构造最大似然空间谱函数

对式(15)进行谱峰搜索,谱峰极大值对应的方位角及仰角即为入射信号的DOA。此处引入极化滤波是利用了各诱饵的极化信息基本相同这一特性,可以有效地抑制雷达的极化信息对有源诱饵极化信息的影响。

2.4 基于斜投影的信号角度估计

假设K个远场入射窄带完全极化信号中存在M个未知信号,已知信号数量为K-M,可将阵列流型改写为

利用估计得到的已知诱饵的空域和极化域信息,构造信息已知的K-M个诱饵信号的导向矢量

首先对混叠信号前沿段X1234在H上进行正交补投影,得到投影信号1234,即

式中:P⊥表示正交补投影矩阵。

式中:Us1为未知信号子空间;Us2为已知信号子空间;Λs1为M个大特征值构成的对角阵;Λn为N-K个小特征值构成的对角阵。

依旧取低秩空间为噪声子空间Un。根据子空间类算法原理,信号子空间和噪声子空间正交。可以利用已知的K-M个诱饵信号的导向矢量H作为约束,约束传统极化敏感阵列MUSIC 算法中的噪声子空间,使其正交于方向已知的诱饵信号导向矢量H。这个约束可通过把阵列输出信号矢量X的列空间投影到已知信号的导向矢量H的列空间的正交补空间上来实现。

再考虑斜投影,抑制已知信号对未知信号的影响,进一步压缩噪声子空间。

传统极化敏感阵列MUSIC 算法的子空间分解类算法是利用信号子空间与噪声子空间的正交性,对MUSIC算法的目标函数fMUSIC求最小值,即

而H可以由前沿诱饵信号估计得到,故可作改进,选择目标函数

式(21)也可换一种形式,表示为

式中:ξ为系数矢量。

为了抑制已知信号对未知信号估计结果的影响,进一步考虑极化MUSIC 算法的目标函数fP-MUSIC,有

最终可以推得

式中:P为投影矩阵;†为广义逆运算符。

由上述分析可知,对fP-MUSIC进行二维谱峰搜索即可获得雷达信号的空域角度信息。

3 仿真分析

(1) 仿真条件

假设使用3个诱饵掩护1个目标雷达,各诱饵的极化参数完全相同,与空间排布无太大关系,主要与时序有关。其中,诱饵1在时序上超前于目标雷达、诱饵2和诱饵3的时间为t1,诱饵及目标雷达信号波形理想情况下的叠加示意图如图2所示。

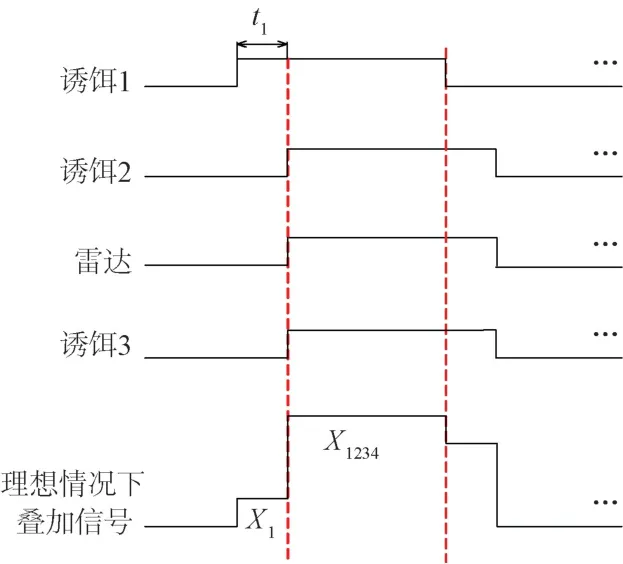
图2 理想情况下各信号脉冲波形叠加示意图

设接收阵列为七阵元极化敏感均匀圆阵,直径为150 mm。3个诱饵和1个目标雷达的方位角及仰角分别设置为(45°,75°),(135°,75°),(315°,75°),(225°,75°)。目标雷达辐射信号的载频为4.5 GHz,诱饵发射信号的载频约为4.5 GHz,两者频差(3～5)MHz,相位抖动30°,通道不一致性偏差7°,入射信号与噪声统计独立。

(2) 极化MUSIC空间谱估计

对多个信号混叠的脉冲直接进行极化MUSIC空间谱估计,得到的空间谱如图3所示。

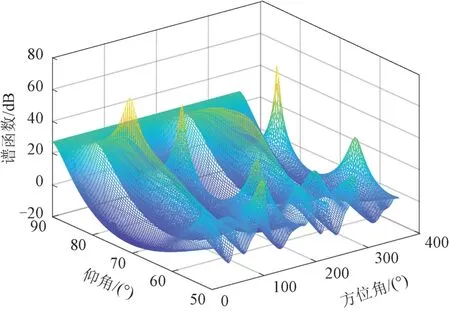
图3 极化MUSIC估计的混叠信号空间谱

由图3分析可知,根据式(8)直接进行空间谱估计,除了实际谱峰以外,还有多处伪峰。可见直接利用极化MUSIC算法的空间谱估计存在严重的角度估计不准的问题。

(3) 极化滤波+斜投影空间谱估计

对混叠信号的前沿段进行极化MUSIC空间谱估计,得到的三维谱图如图4所示。以前沿段估计的极化参数为约束,对信号叠加段进行极化滤波后,再进行极化MUSIC空间谱估计,得到的三维谱图如图5所示。进行斜投影以后,再进行极化MUSIC空间谱估计,得到的三维谱图如图6所示。

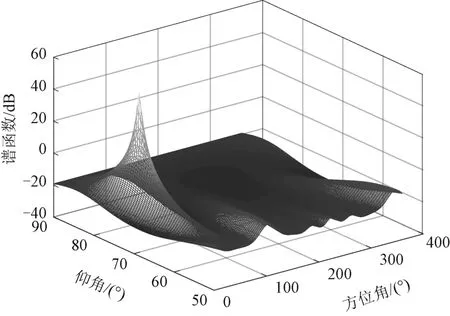
图4 极化MUSIC估计的前沿段信号空间谱

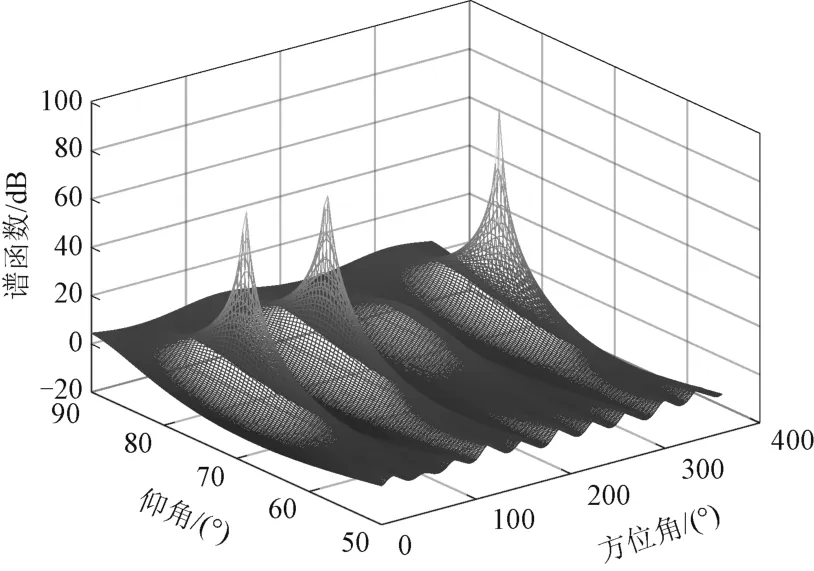
图5 极化滤波后极化MUSIC估计的叠加段信号空间谱

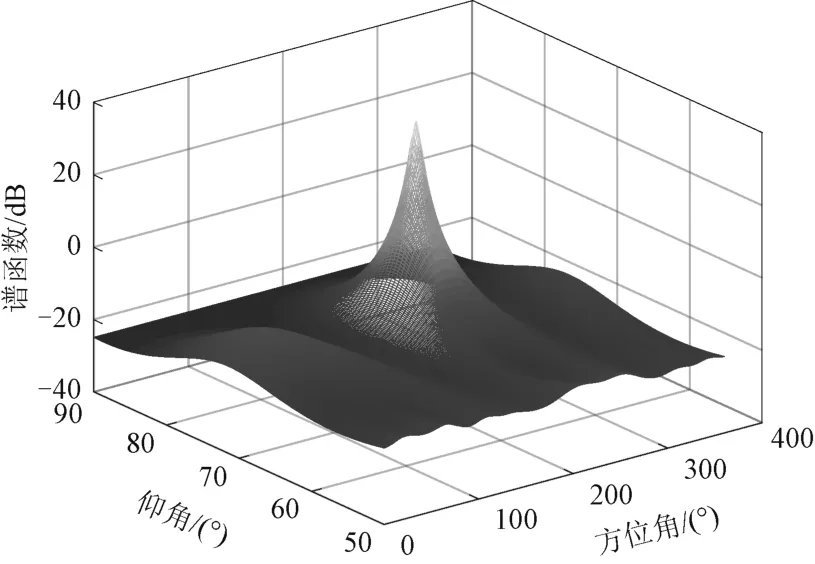
图6 斜投影后极化MUSIC估计的叠加段信号空间谱

由图4～图6可知:极化滤波能起到很好的抑制雷达信号的效果,使对诱饵的DOA 的估计更为准确;而斜投影算子的引入抑制了已估计的诱饵信号对待估计雷达信号的影响,使得目标雷达的DOA 估计更为准确。

4 结论

由仿真实验可知,对包含多个信号的混叠脉冲信号,直接应用极化MUSIC算法进行DOA 估计是不准确,甚至是错误的。而引入极化滤波与斜投影算子,可以较为准确地分辨出多个信源的DOA。极化MUSIC 算法中,对极化维的处理涉及两个方面:一是对混叠信号前沿段的DOA 与极化参数进行估计;二是应用前沿段的极化参数作为诱饵及信号子空间的约束,对混叠信号的叠加段进行极化参数滤波,更准确地估计出诱饵信号的DOA。由此可见,极化MUSIC 算法是对MUSIC 算法的改进与提升,具有更好的适用性。斜投影算子的引入,本质是沿着与已估计出的诱饵信号子空间平行的方向,将其投影到待估计的雷达信号子空间中。在估计雷达信号DOA 时,抑制了诱饵信号对目标雷达信号DOA 估计的影响,使得对雷达信号的DOA 估计更为准确,实现多目标的有效分辨。