基于BP神经网络的电动汽车电子差速器设计

李全民

（广州理工学院智能制造与电气工程学院，广州 510540）

0 引言

汽车差速器能使左右驱动轮自由转动，以便在转向行驶、路面起伏、轮胎差异等情况下驱动轮不会发生滑转或滑移，确保稳定性。传统燃油汽车的驱动轮由半轴和主减速器等部件连接在一起，一般使用机械差速器，使左右驱动轮能自由转动并平均分配驱动转矩［1］。对于分布式前驱动电动汽车而言，其两驱动轮分别由两个电机单独驱动，没有传统差速器的机械连接，其功能完全可由计算机实现，即电子差速控制。

目前电子差速器的控制策略大致分为转速控制和转矩控制两类。转速控制一般根据Ackerman 转向模型推导出左右车轮之间的转速约束关系n1=f（n2），然后据此设计电子差速器，输出为左右车轮的转速。但Ackerman 只是简化的理想模型，没有考虑汽车转向时的离心力、汽车侧倾、轮胎变形等因素，只能适用于汽车低速行驶的情况。转矩控制考虑的因素比较多，一般要建立汽车动力性模型，因而控制系统非常复杂，技术难度大，动态的实时性也比较差。

神经网络控制是近年来兴起的先进控制技术，作为智能控制的一个分支，具有高度非线性逼近能力，为解决复杂的非线性、不确定性、不确知系统的控制开辟了新的途径。采用神经网络系统控制汽车内外轮转速，可实现汽车动力系统中未知部分的在线精确补偿。下面利用BP（back propagation）神经网络，根据非线性动力系统辨识理论来设计电子差速器。

1 汽车转向Ackerman模型分析

图1为典型的汽车前轮差速Ackerman 转向模型［2］，图中r为质心的转向半径；θ为电动汽车的转向角，即给定转向角度；o为电动汽车的转向圆心；θ1、θ2分别为前左和前右两转向轮的转向角度；G为电动汽车的质心（假设质心在车体的中心）；a、b分别为轮距和轴距；V为转向时的质心速度，即整车车速；r1、r2、r3、r4分别为四个车轮的转向半径；V1、V2、V3、V4分别为四个车轮的速度。

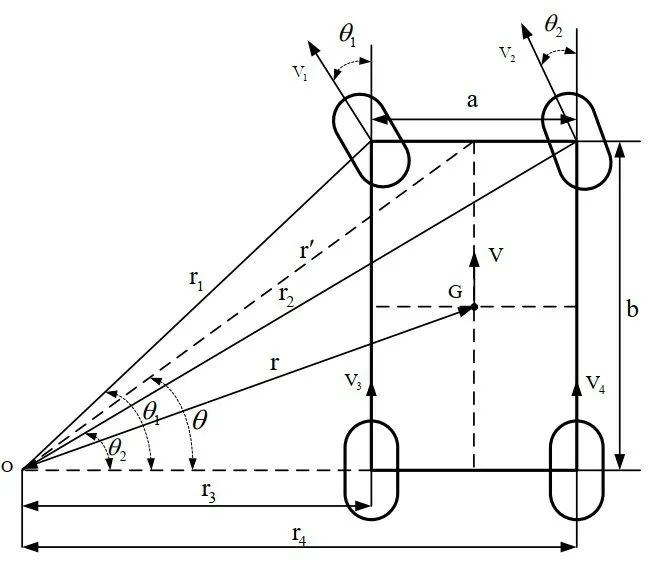
图1 汽车前轮差速Ackerman转向模型

四个车轮的转向半径依次为

整车质心的转向半径为

由上式可得四个车轮的速度依次为

把车轮的转向半径公式和整车质心的转向半径公式带入车轮的速度公式可得四个车轮的速度依次为

在上述公式中，电动汽车的轮距a和轴距b均为常数。因此，对于一个具体的4 × 2 前驱电动汽车而言，前面两个转向驱动轮的速度只取决于整车车速V和转向角θ。同时，根据汽车理论［1］知识，影响电子差速器设计的其它因素比如离心力、载荷转移、汽车侧倾、轮胎变形等，也是由这两个变量引起的。因此，整车车速V和转向角θ是电子差速器设计的主要参数，这就为基于神经网络设计电子差速器时的样本取得奠定了理论基础。

2 神经网络样本数据获取［3］

针对使用不同驱动控制系统的电动汽车，文献［3］设计了一个通用的车辆行驶参数测量系统，该系统的结构如图2所示。测量时整车速度V的范围取0～25 m/s，转向角θ范围取0°～20°。根据不同整车速度和转向角，分别测得不同的前面两个驱动转向轮的速度，共测得24组数据，经过归一化处理，得到神经网络的学习样本如表1所示。

表1 神经网络学习样本

图2 神经网络样本获取系统结构

从表1可以看出，汽车转向时左右侧前轮转速V1、V2与车体质心速度V和转角θ之间不是线性关系，并且也不完全符合Ackerman 模型。这主要是由于Ackerman 模型没有考虑汽车转向时的离心力、载荷转移、汽车侧倾、轮胎变形等因素。

3 基于BP神经网络的电子差速器设计

神经网络具有大规模并行计算能力，冗余性和容错性强，其本质上具有非线性，且具备自组织、自学习、自适应等能力，适合处理那些影响因素众多、难以用模型描述的过程或系统。电动汽车的电子差速器就是这样一种系统，而BP 神经网络是神经网络中比较成熟的一种。使用表1中的数据对神经网络进行训练，就能得到各神经元之间最优连接权值，即辨识了电子差速器的运行模式。

3.1 BP神经网络模式辨识算法［4］

BP神经网络结构如图3所示。

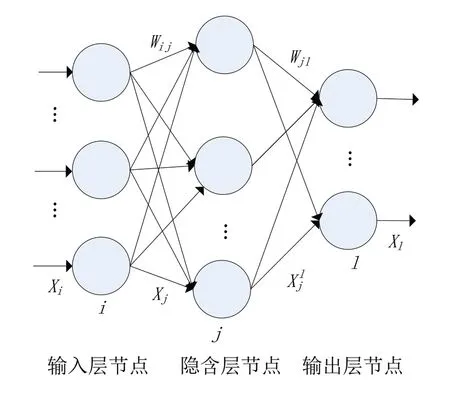
图3 BP神经网络结构

3.1.1 向前传播：计算网络的输出

隐层神经元的输入xj为所有输入xi的加权之和：

则

输出层神经元的输入为

网络第l个输出xl与相应理想输出的误差为

第p个样本的误差性能指标函数为

其中：N为网络输出层的个数。

3.1.2 向后传播：采用梯度下降法，调整各层间的权值

输出层与隐层间连接权值wjl学习算法为

其中：η为学习速率，η∈[0,1]。k+1 时刻的权值为

隐层与输入层间连接权值wij学习算法为

其中：

k+1时刻的权值为

如果考虑上次权值对本次权值变化的影响，需要加入动量因子α∈[0,1]，此时的权值为

3.2 神经网络训练和测试

设计使用3 层BP 神经网络结构，输入层、隐层和输出层的神经元数目分别为2、4、2，即网络结构为2-4-2。神经网络中每一层神经元的状态只对下一层神经元的状态产生影响。输入为车体质心速度V和转角θ，输出为内外向驱动轮的速度V1、V2。权值wij、wjl的初始值 取［-1,+1］之间的随机值，学习速率η取0.5，动量因子α取0.05。

在Matlab 环境下用BP 神经网络对电子差速器的运行模式进行辨识［4］，主要包括网络训练程序和网络测试程序。训练程序的最终指标取E= 0.005。样本的训练过程如图4 所示，结果显示其收敛速度很快。经过训练得到的网络权值如表2、表3所示。

图4 样本训练的收敛过程

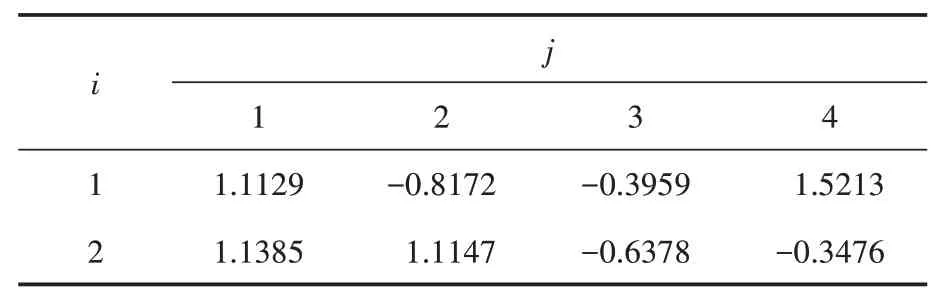
表2 输出层与隐含层之间的权值Wij

表3 隐含层输出层之间的权值Wjl

测试BP 网络时，整车速度V的范围取0～25 m/s，转向角θ范围取0°～20°，各取等分17个数据，总共289 个数据，归一化后用表2 和表3 中的连接权值进行计算。计算结果如图5 所示，其中（a）、（b）两幅子图分别对应内、外转向轮车速与转向角和整车车速的关系（其中每一行代表一个整车车速，从下到上整车车速增加），从图5 可以看出，汽车转向行驶时，对应同一个整车速度，外侧驱动轮转速增加，内侧驱动轮转速减小，外侧车轮增加的值和内侧车轮减小的值近似相等，方向盘转角越大，差速越多；对应同一个转向角，车速越大，差速越多。测试结果显示，该BP 神经网络差速器输出结果符合车辆转向行驶时的运动特性［1］。

图5 内外转向轮车速与转向角和整车车速的关系

3.3 神经网络电子差速器设计

图6为基于BP 神经网络的分布式驱动电动汽车电子差速器设计方案［5］，输入为整车速度V和转向角θ，输出为内外转向轮车速V1、V2。对于任意一组允许范围内的整车速度和转向角，该BP 神经网络差速器都可实时计算出汽车转弯时准确的内、外侧转向轮转速，作为分布式独立驱动双电机控制器的内、外侧转向驱动轮的给定速度。

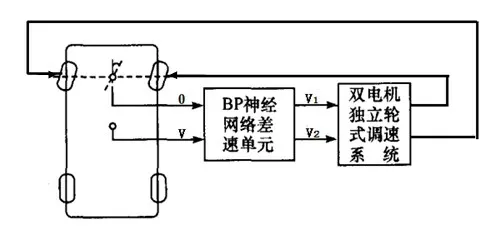
图6 采用BP神经网络电子差速器示意图

4 结语

通过对汽车转向Ackerman 模型的分析，得到了电子差速器设计的两个主要考虑因素，即整车速度和转向角；设计了能用于电子差速器的BP 神经网络架构，编写了神经网络Matlab 程序，利用样本数据训练得到了最优权值并进行了测试，结果表明神经网络差速器真实地反映了内外驱动轮转速与整车速度和转向角之间的非线性关系，能有效实现差速；最后提出了一种用于分布式驱动电动汽车的BP 神经网络差速器设计方案。