基于深度学习的单层双阻带频率选择表面设计

黄 钰，石 锋，闫丽萍

（四川大学电子信息学院，成都 610065）

0 引言

随着5G 无线技术在大数据、物联网等领域的广泛应用，越来越多的设备参与到5G 通讯中来，空间中电磁辐射源日益增加［1］。目前国内已经广泛商业化的5G 工作频段均处于FR1（0.45～6 GHz），即Sub-6 GHz频段。随着卫星通信应用的日益广泛，工作在Ku 波段（12～18 GHz）的通信设备因其天线小型化而获得市场青睐［2］。因此能够同时抑制这两个工作频段的双阻带电磁屏蔽结构日益受到关注。传统的电磁屏蔽技术常使用金属外壳保护敏感电子设备免受外界电磁干扰。该类屏蔽技术在全频段范围进行电磁防护，无法用于带内通信带外抑制的电子系统，且结构重。采用周期排列的二维人工结构实现的频率选择表面（frequency selective surface，FSS）依靠其独特灵活的选频特性获得了越来越多研究人员的关注，已被应用于电磁干扰抑制领域。

在双阻带FSS的研究上已经有大量工作在不同频段的双阻带FSS结构。2018年，Mutluer等［3］通过单元结构组合方式，获得了一个工作在Ku波段14.5 GHz和Ka波段34.5 GHz的双阻带FSS结构，其3 dB 屏蔽效能带宽分别为3.1 GHz 和4.1 GHz，具有良好的极化稳定性和60°角度稳定性。Khan 等［4］将开口方环与T 型图案进行组合，并通过旋转得到了一个四元单元结构。该结构工作在X 波段7.23 GHz 和Ku 波段13.83 GHz，其3 dB 屏蔽效能带宽分别为1.2 GHz 和0.8 GHz。2020年，Wang等［5］使用弯折方环实现了单层FSS双阻带结构，分别工作在3.4 GHz和4.9 GHz，并具有60°的角度稳定性。Sun等［6］通过组合两个方环结构，实现了3.5 GHz 和4.86 GHz 双阻带FSS结构，其25 dB 屏蔽带宽可达1.17 GHz 与0.67 GHz，并能提供40°的角度稳定性和极化稳定性。以上双阻带FSS结构或工作在Ku及以上频段，或同时工作在FR1频段，还未见有同时对FR1与Ku频段进行屏蔽的单层FSS报道。

随着工程需求的不断发展，FSS的单元结构变得越来越复杂，性能分析难度大大增加。人工智能在其他领域的卓越表现，使研究人员也开始将神经网络引入对FSS的分析之中［7］。2020年，Arya 等［8］针对偶极子单元结构，建立了预测反射系数S11的神经网络模型。该模型以偶极子的结构参数作为输入，反射系数S11值作为输出，使用神经网络误差参数值作为参考来判断是否预测成立。Zhu 等［9］构建了一个多层FSS 结构的神经网络，实现了对指定S21参数性能的固定单元结构的FSS结构预测，提高了FSS结构设计速度。该网络将S21进行定长取值作为网络的输入，FSS 的结构参数作为输出。由于FSS 的结构不变，保证了这种对S21固定取值的方式能够保留S21的信息。2021 年，Chaudhary 等［10］提出了一种多层的THz 吸波器，并构建了神经网络模型以替代传统的优化算法。该网络以各层FSS结构参数作为输入，吸收频带的中心频率与带宽作为输出。经过大量数据的训练，训练完成的神经网络可以在短时间内获得优化结果。2022年，Gu等［11］提出了一种四边向内弯折的FSS结构，对其构建神经网络以取代传统的调谐迭代优化方式。该神经网络以FSS的结构参数作为输入，S21曲线值作为输出。经过训练后的网络模型配合遗传算法可以快速优化获得合适的结构参数。以上研究表明，神经网络在FSS的分析与设计中具有重要应用价值。通过构建恰当的神经网络模型获取参数之间的关系，可以实现对FSS结构性能的预测和优化，进而提高设计效率，为复杂FSS的研究提供了一种新的途径［12］。

因此，本文提出了一种可同时覆盖Sub-6 GHz与Ku 波段的单层双阻带FSS 结构，并构建反向传播深度神经网络（back propagation deep neural network，BP-DNN）模型，学习结构参数和电磁性能之间的关系。所设计的FSS 结构低频可屏蔽0～5.5 GHz 频段，高频可通过调节金属臂长度在12～21 GHz 范围内阻带可调。利用训练后的BP-DNN 模型，可以快速获得指定Ku 波段工作频点所需的金属臂参数。

1 FSS结构设计

考虑到Sub-6 GHz频段覆盖的相对频段范围较大，因此直接采用具有高通低阻特点的金属栅网结构实现该频段电磁干扰的抑制。即FSS单元结构（见图1）包含一个金属方环，且该金属方环与相邻单元的金属方环相连接形成金属栅网，如图1（c）阴影部分所示。通过调整单元结构尺寸L和方环宽度Wr的大小，栅网结构可以实现对0～5.5 GHz 的频带覆盖。在此基础上，四根金属臂从方环四边的中心处延伸出来，以获得Ku 波段阻带。由此构成的FSS 单元结构正视效果见图1（a）。所提出的FSS 结构蚀刻在介电常数为4.3、损耗角正切为0.02 的FR4 介质基底上。整个FSS 结构呈现出中心对称的特点，确保该结构具有良好的极化稳定性。采用弯折方式的小型化设计使得金属臂能够放置于方环内部，并有利于该FSS结构的角度稳定性。

图1 单层FSS的单元结构

当导带宽度固定时，金属臂的长度L1、L2、L3、L4、L5将决定高频阻带的谐振频率。为了快速调节金属臂长度以获得所需阻带性能，需获得结构参数与S参数频率响应之间的关系。常见FSS分析方法在复杂单元结构的应用上存在许多限制和困难。例如，等效电路法通常会将单元结构的各个部分等效替换为电容、电感等电子元件，并分析由这些元件组成的等效电路以简化对FSS 传输特性的分析。然而，对于形状不规则或非条带状的单元结构，很难确定单元结构与其等效集总元件之间的解析关系式。且对于复杂FSS 单元结构，常常需要借助全波分析方法来提取其等效集总元件参数。全波分析法是计算获得FSS 性能的有效方法，但对于复杂FSS单元结构计算耗时长。深度神经网络含有许多隐藏神经元，能够学习复杂的参数关系。因此，本文采用深度神经网络建立二者之间的关系模型，主要用于分析弯折金属臂结构尺寸与Ku波段的性能。

2 深度神经网络

2.1 深度神经网络结构设计

图2（a）展示了一个神经元的基本结构。该神经元的输出可表示为

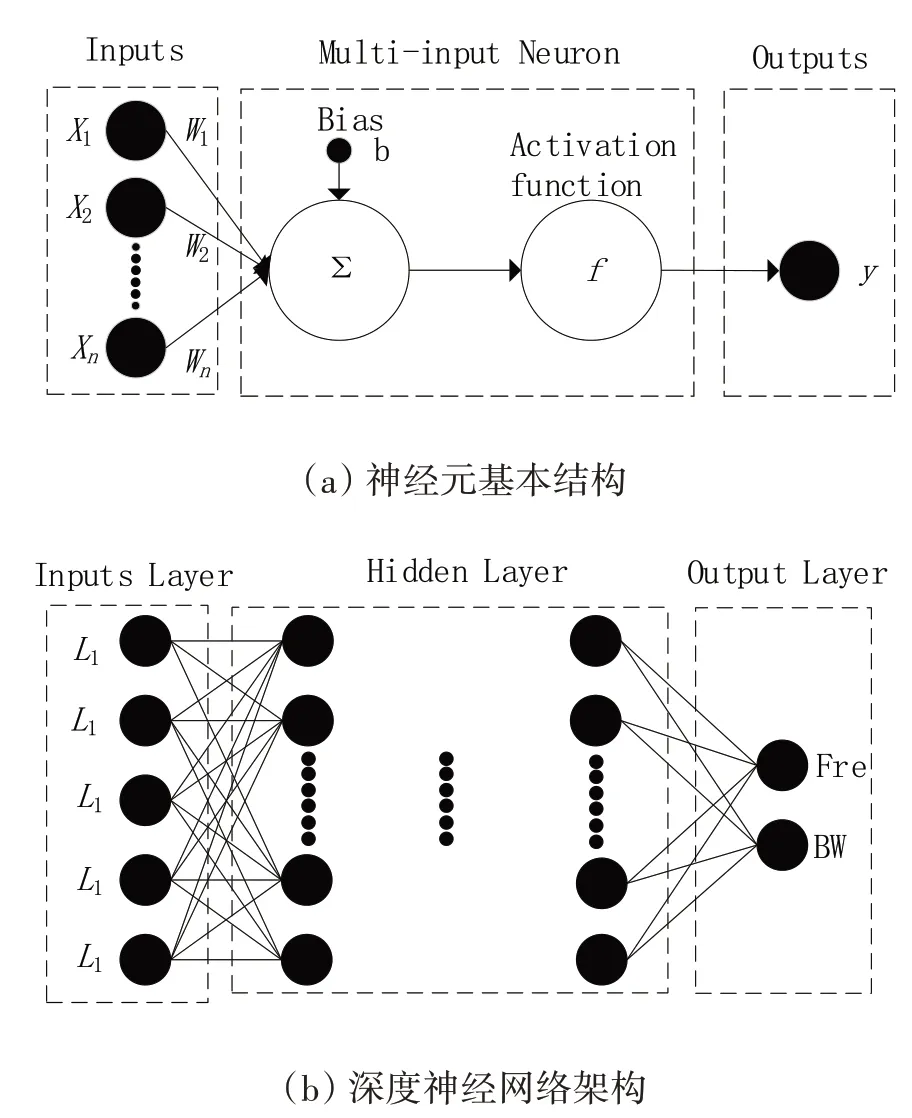
图2 深度神经网络示意图

式中：X与y分别表示输入和输出；W为权重；b为偏置；f表示为激活函数。

图2（b）展示了本文所提深度神经网络模型的构架。输入数据为金属臂五个组成部分的长度，输出数据为TE极化波垂直入射时FSS结构在Ku 波段阻带的中心频点f0及其15 dB 屏蔽效能带宽。整个网络模型的工作流程是：输入数据沿着传播方向进行传播，每个神经元通过式（1）计算其他神经元传入的值并输出给下一层神经元，在输出层得到预测值。使用BP（Back Propagation）算法对权重值进行更新，即根据预测的f0和| |S21≤-15 dB带宽与实际值之间的误差值，沿着相反传播方向更新权重值，完成一次训练。这个过程重复进行多次，直到模型达到预期性能。

所提出的BP-DNN模型使用Python编写的开源人工神经网络库Keras 进行构建，采用Adam算法取代传统的随机梯度下降算法。该算法能够根据训练数据不断更新各个神经元的权重，其学习率为0.001。损失函数使用均方误差值（见式（2））计算，式（2）中n为每次的训练次数，为预测值，yi为实际数据值。

构建的BP-DNN 模型隐藏层神经元参数如表1 所示。其中Numbers 代表该层神经元个数，Parameters 代表该层神经元可训练的参数个数。整个隐藏层中共有88134个可训练参数。

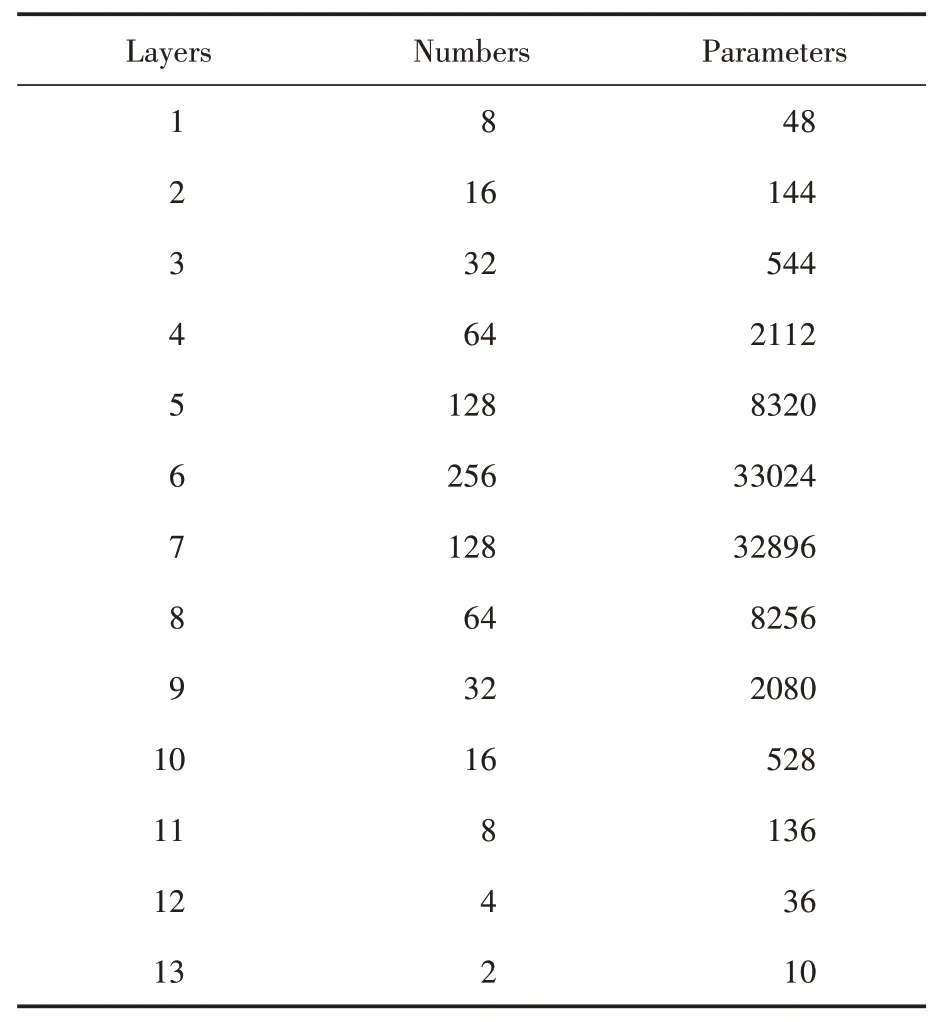
表1 隐藏层神经元参数

2.2 训练深度神经网络

根据FSS 单元结构及其周期，表2 给出了金属臂五个部分长度的取值范围，每个参数在给定范围内等步长取值。考虑到结构周期限制和加工精度，L1和L3取5 个样本值，L2和L4取4 个样本值，L5取3个样本值。这些参数的组合将形成BP-DNN 网络的数据库，共计1200 组数据。在训练过程中，只有输入数据会发生变化，其余FSS结构参数保持不变，分别为：h=1.6 mm，t= 0.002 mm，Wr= 0.4 mm，w= 0.2 mm。使用数据库中1000 个（占83%）数据作为训练集，剩余的200个（占17%）作为测试集。每次从数据库中取128 组（epoch）数据进行训练以更新各神经元权重，共计进行5000次（batch size）的训练。

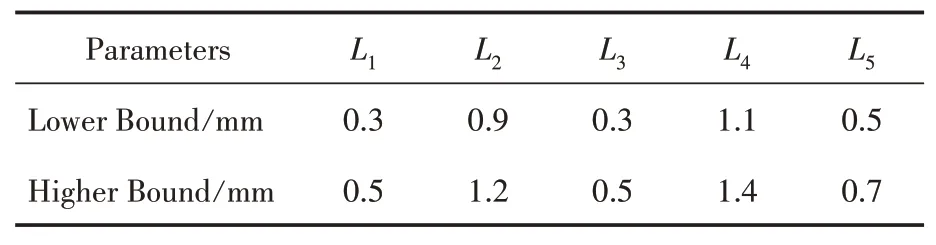
表2 输入参数取值范围

2.3 深度数据网络训练结果

最终的训练结果如图3所示。

图3 DNN网络MSE值随训练次数的变化曲线

其中图3（a）展示了5000 次训练中MSE值的变化，可以观察到损失函数的值随着训练次数的增加迅速减小。图3（b）给出了最后1000 次训练中MSE值的变化，虽然MSE的值仍有起伏但整体仍呈现下降趋势，说明所构建的FSS 结构BP-DNN 网络学习过程中在不断尝试不同的权重选择，并最终达到MSE= 0.001。将测试集200组数据中的金属臂参数作为深度神经网络的输入预测Ku波段阻带的中心频率f0和 |S21|≤-15 dB

带宽，并与200组数据中的性能参数进行比对计算。中心频率的平均误差为0.08 GHz，最大误差为0.21 GHz；带宽的平均误差为0.06 GHz，最大误差为0.28 GHz。由此可见，所构建的FSS结构BP-DNN网络通过训练学习得到了金属臂参数与中心频点和带宽之间的关系，在所提供的参数范围内取得了良好的预测效果。

3 验证深度神经网络

为了进一步验证该BP-DNN 网络在FSS 结构设计方面的可行性，设定目标性能让神经网络进行预测。训练集的Ku 波段阻带中心频率变化范围为12～21 GHz，这里设定FSS 的目标性能为：f0= 16 GHz，| |S21≤-15 dB 带宽为1.8 GHz。基于所提BP-DNN 网络的FSS结构设计流程如图4 所示。首先，根据FSS 单元结构及其周期，通过Python语言编程得到满足结构周期限制与加工精度的结构参数集。然后使用神经网络对该参数集进行预测，将符合预设性能值所对应的结构参数值作为预测结果。最终通过神经网络获得的对应结构参数如表3所示，使用BP-DNN 网络的预测阻抗中心频率为f0=16.04 GHz，|S21|≤-15 dB带宽1.86 GHz，满足设计要求。

图4 基于BP-DNN网络的FSS结构设计流程

表3 结构参数

采用全波分析方法对基于BP-DNN网络的单层双阻带FSS 结构性能进行计算，结果如图5所示。可以看出，利用BP-DNN 网络设计的FSS 结构，电磁波垂直入射情况下，两种极化方式下|S21|≤-15 dB带宽分别为0～5.5 GHz和1.9 GHz，且Ku 波段阻带中心频率为f0=16.04 GHz。该结果与BP-DNN网络的预测值非常吻合，验证了所提BP-DNN 网络在单层双阻带FSS结构性能预测方面的可行性。由图5 还可以看出，所设计FSS结构在TE和TM两种极化方式下具有良好的角度稳定性，保持 | |S21≤-15 dB带宽不变的入射角度高达40°，且覆盖了几乎全部Sub-6 GHz频段。

图5 FSS结构的传输系数

4 结语

本文提出了一种工作在FR1 与Ku 频段，具有40°角度稳定性和良好的极化稳定性的单层双阻带FSS 结构，并通过构建BP-DNN网络实现了对指定Ku频段阻带的FSS结构参数预测。所设计FSS结构FR1阻带可覆盖0～5.5 GHz，Ku阻带中心频率可在12～21 GHz范围内通过金属臂长度调整。利用训练好的BP-DNN 网络，可快速获得FSS 单元Ku 波段指定阻带对应的结构参数，为FSS单元结构的快速设计提供了方便。全波分析结果证明基于BP-DNN 网络快速设计获得的FSS结构完全满足指定性能要求。后续工作可将更先进的DNN算法与FSS结构设计相结合，以实现性能优越的复杂FSS结构的智能设计。