车轮-地面耦合动力学行为的CDEM-DEM 分析

路 扬，冯 春，程鹏达，张一鸣

（1.河北工业大学 土木与交通学院，天津 300401；2.中国科学院 力学研究所，北京 100190；3.中国科学院大学 工程科学学院，北京 100049）

1 引言

越野车具有车身为非承载式、车身底盘高、轮胎抓地性好等优点，能够适用于各种恶劣的道路环境。车辆在软土路面行驶的过程中，其车轮下陷深度、车辆通行速度、轮胎胎面花纹、地面特征及其相互作用，都会对汽车正常行驶产生一定影响。近年来随着社会的发展，车轮-地面作用的研究也尤为重要。

针对此类问题，国内外学者进行了大量研究工作。臧孟炎等 人［1-3］基于有限 元（Finite Element Method，FEM）和离散元（Discrete Element Method，DEM）进行了大量仿真分析，通过探究其制动性能和动态特性等，证明了采用数值模拟方法对车轮-地面动态力学行为进行分析的有效性，并对于越野轮胎进行沟槽设计的必要性提出了合理解释；Zeng 等人［4］基于DEM-FEM 耦合模型通过三轴试验调整模型参数，证明了该模型对于轮胎-地形相互作用仿真模拟的可行性；Farhadi 等人［5］通过建立轮胎-土壤相互作用的有限元模型并研究了垂直载荷、轮胎充气压力、土壤含水量对轮胎功率损失的影响，由此证实了该功率损失估算模型的可行性；邓露等人［6］基于车辆轮胎相关特征并结合理论推导，提出了一种车轮轮胎的精细化模型，使得其计算结果与实验数据更加接近准确。

车轮-地面力学动态行为的研究在运输业、农业、航天等方面均有重要意义，近年来人们对于该方面的研究越发深入。谢斌等人［7］对国内外研究工作进行了综述，重点讨论了轮胎部分的建模方法并结合当今最新研究成果对未来提出了展望；吕凤天等人［8］通过对车轮-地面进行图像提取，基于视觉即可对月球车车轮滑转率进行估计；姜春霞等人［9］基于单轮土槽实验，对人字形花纹轮胎-地面中的垂直应力分布规律进行了探究；张锐等人［10］基于现场试验和数值模拟相结合，对车轮曲率半径在车轮-沙地作用中沉陷性能的影响进行了分析，为沙地车轮设计提供了理论依据。Guo 等人［11］基于多球DE-FE 方法对于某越野气动轮胎在不规则碎石地形上的牵引性能进行了数值模拟，证明了该方法能够较好地再现轮胎行驶行为。

综合以上结果可以看出，数值模拟方法对车轮通行的仿真模拟计算的可行性具有较为完备的理论依据。但由于车轮与软土路面之间具有较为复杂的动态力学性质，采用单一的有限元方法或离散元方法均无法进行准确刻画。为此，本文结合前人研究成果，提出了一种CDEM-DEM耦合方法，实现了车轮与软土路面的动态耦合，并重点探讨了车轮花纹情况、路障对车轮行进效率、行进能耗的影响。

2 计算方法介绍

2.1 CDEM 方法

连 续-非 连续单元法［12］（Continuum Discontinuum Element Method，CDEM）是一种有限元与离散元相结合的显式动力学数值分析方法，其理论基础为拉格朗日方程，见式（1）：

其中：ui，vi为广义坐标；L为拉格朗日系统的能量；Qi为非保守力做的功。

连续-非连续单元法中的核心控制方程见式（2）：

其中：M，C，K，Kc，Cc和F分别为单元质量矩阵，单元阻尼矩阵，单元刚度矩阵，接触面刚度矩阵，接触面阻尼矩阵和节点外部荷载列阵；分别为单元内所有节点的加速度列阵，速度列阵，位移列阵以及虚拟裂缝上的相对位移列阵，相对速度列阵。

2.2 DEM 方法

DEM［13］是一种显式数值计算方法，通常用于计算颗粒流在相关条件下的力学性能。DEM的基本原理有两个方面：接触模型和运动方程。两种基本原理分别用来求解离散单元的接触力和运动状态物理量（速度、加速度、位移转角等）。

接触模型，即力-位移关系。该关系通过离散单元间的连接模型来表征材料本构关系，其理论公式如式（3）、（4）：

运动方程基于牛顿第二定律，其核心控制方程如式（5）、（6）：

其中：mi为刚体质量；rij为j作用于i上的作用点到i形心的距离；vi，ωi分别为i的速度矢量和角速度矢量；Ii为i的惯性矩；g代表重力加速度；t代表时间。

2.3 CDEM-DEM 耦合方法

CDEM 与DEM 分别可对块体有限元和颗粒离散元的力学行为进行计算，将两种方法有机耦合，即可对车轮-地面力学动态行为进行准确刻画。如图1 为CDEM-DEM 耦合方法示意图。

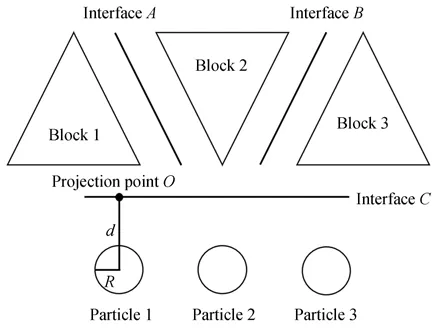
图1 CDEM-DEM 耦合方法Fig.1 CDEM-DEM coupling method

其中，上半部分CDEM 模型包括块体和界面两部分，块体由有限元单元体所组成；界面为块体间的公共边界，分别表征材料的弹性、塑性、损伤等连续特征和断裂、滑移、碰撞等非连续特征。数值模拟时，车轮采用CDEM 块体进行描述，软土路面采用DEM 颗粒进行描述。块体与颗粒、颗粒与刚性面之间接触耦合刚度采用全局的值，法向、切向刚度均为1×109Pa·m-1。节点力和节点运动的核心控制方程见式（7）、（8）。基于以下方程即可实现显式求解过程。

其中：F为节点合力，FE为节点外力，Fe为有限元单元变形贡献的节点力，Fc为接触界面贡献的节点力，Fd为节点阻尼力，a为节点加速度，v为节点速度，Δu为节点位移增量，u为节点位移全量，m为节点质量，Δt为计算时步。

CDEM-DEM 耦合方法主要包含接触检测与接触力计算两部分，其中接触力计算与颗粒离散元间接触力［14］一致，均为基于增量法的显式求解方式，其计算式见式（9）、（10）：

其中：Fn，Fs分别为颗粒间的法向和切向接触力；Δt为计算时步；Δdun，Δdus分别为两个接触颗粒间的法向和切向位移增量差。

接触检测首先基于子空间法，通过颗粒、块体等之间的映射关系缩小检测范围，之后，进行精确检测。在本文的车轮-地面问题中，该接触检测即是有限元与边界面之间的接触，一般采用点-面接触模型［15］实现。其需要满足如下两个基本条件：

其中：d为颗粒体心到边界面的距离，R为颗粒球体半径，C为边界面，O为颗粒体心在边界面上的投影位置点。

2.4 动态边界条件施加

由于CDEM 中的单元只有平动自由度，没有转动自由度，无法直接对CDEM 单元施加扭矩；为此，本文提出了一种在局部坐标系下施加动态切应力，从而间接施加动态扭矩的方法。在车轮轮毂面施加线性变化的动态边界条件从而牵引车轮转动，开启坐标系施加开关，在两个切向上施加动态边界条件。其核心控制方程如式（13）：

其中：Fi为第i方向的载荷值（面力）；fT0，fT1分别为线段起始时间和结束时间；fV0，fV1分别为线段起始值和线段结束值；λi为各个方向的载荷系数；t为当前时间。

图2 为动态边界条件施加方式示意图，在该模型中，通过在车轮轮毂中心圆柱面设定坐标系以确定法向与切向，在圆柱面上施加切向面力从而产生转矩使车轮转动。

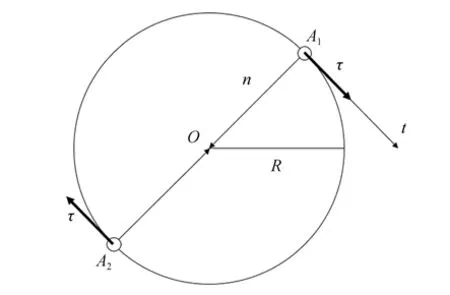
图2 动态边界条件施加方式示意图Fig.2 Schematic diagram of application mode of dynamic boundary conditions

通过在圆柱面每一个节点施加面力，对所有面力进行求和形成转矩，其主要控制方程如式（14）、（15）：

其中：Fi为作用面力，Ai为面力作用的面积，τ为切应力，M为转矩，R为圆柱面半径。

转速力矩控制方程如式（16）、（17），通过推导得出转速切应力关系如式（18）：

其中：β为角加速度，J为转动惯量，m为质量，ω为转速，t为时间，ρ为密度。

创建圆柱体车轮进行验证，车轮截面半径R为0.5 m，高h为 0.2 m，密度为1 000 kg·m-3，在圆柱体外环施加局部坐标系下动态切应力1 000 Pa，根据上述方程求得转速预测结果。图3 为预测与模拟结果对比图。

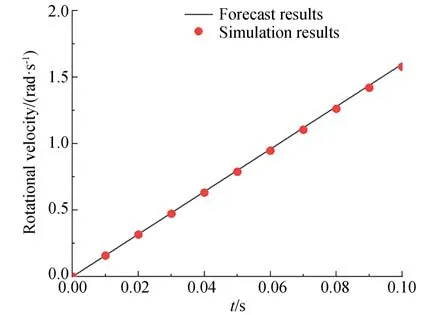
图3 预测与模拟结果对比Fig.3 Comparison of prediction and simulation results

数值计算结果与理论解基本一致，表明了本文提出的利用局部坐标系下切向应力施加扭矩的计算方法的正确性。

3 仿真模拟分析

3.1 模型建立及材料参数

车轮模型尺寸采用了8.25R16LT 132/128F 18PR 全钢载重子午线轮胎［16］。该轮胎外直径855 mm，断面宽230 mm，为简化计算，同时使车轮嵌入地面时车辙更加明显，花纹节距数采用20，其余参数不变。花纹车轮模型见图4，同时建立如图5 所示光面车轮进行对比分析。

图4 花纹车轮模型Fig.4 Patterned wheel model

图5 光面车轮模型Fig.5 Glossy wheel model

其中，轮胎材料选取隔振橡胶［17］，采用linear线弹性本构。对轮胎材料进行均一化假设，将其弹性模量调整至充气状态标准；软土路面采用石灰 土［18］，采 用brittleMC 脆 性断裂 本构。石灰土模型长3 m，宽1 m，高0.14 m。材料力学参数见表1。

表1 材料力学参数Tab.1 Material mechanical parameters

假定汽车重量为3.30×103kg，在轮胎中心建立一组同心圆柱轮毂模型以增加车轮重量使之达到四分之一车重，故需进行等效施加较大转矩使其车速符合实际情况。经实验，当局部坐标系下动态切应力大小在全程恒为10 MPa 时，车轮转速将稳定于11.00 m·s-1，适用于汽车在软土路面行驶时的车速。

在此基础上，在模型周围创建5 个刚性面进行约束。为便于计量，记花纹轮胎工况为T1，光面轮胎工况记为T2，二者初始埋深约为0.03 m。其最终计算模型分别如图6 和图7 所示。

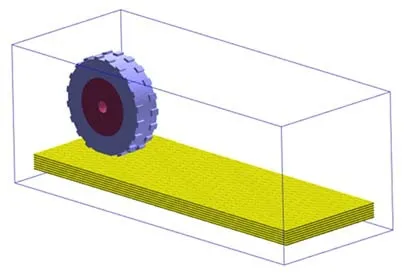
图6 T1 计算模型Fig.6 T1 calculation model

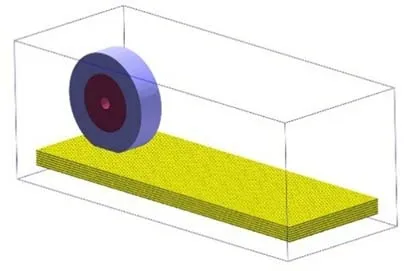
图7 T2 计算模型Fig.7 T2 calculation model

3.2 模型验证

如图8 为本次模拟结果与实验结果对比图（以T2 为例），在计算过程中，与车轮接触的软土路面分为如图8（b）中两个区域，即前区顺时针区和后区逆时针区。如图，T2 在t=0.40 s 时产生颗粒飞溅现象，其前方软土运动方向为顺时针；后方软土产生逆时针方向运动趋势导致车轮后方软土产生堆积现象。该现象与文献［2］中所述实验结果相同。

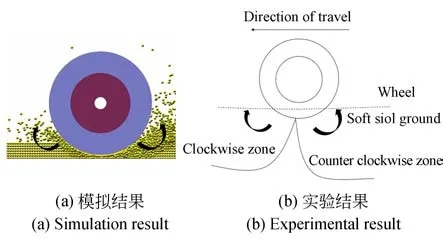
图8 模拟结果与实验结果对比Fig.8 Comparison between simulation result and experimental result

由此可见该计算方法可准确模拟车辆在软土路面行驶的真实情况。

4 计算结果

4.1 T1、T2 工况对比

本次计算过程中，车轮在石灰土软土路面上行驶，待车轮转动至终点计算完毕。如图9～10为计算的两组工况车辙图。从图中可以看到，软土路面由于车轮驶过产生颗粒的挤压流动导致车轮两侧和后侧产生颗粒隆起现象，在地面上留下了清晰可见的车辙。在相同时间内，T1 在软土路面运行完毕到达终点共耗时1.90 s，其运行长度为2.15 m；而T2 在此期间仅运行了0.72 m。由此可见在软土路面上，花纹轮胎的通行能力较光面轮胎更为出色，相同时间内其通行路程更远。

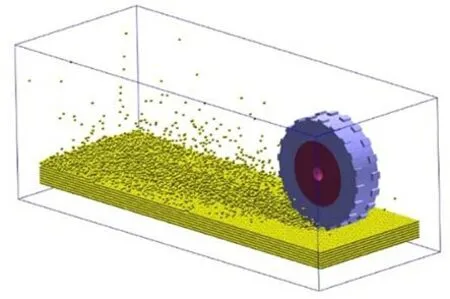
图9 T1 车辙Fig.9 T1 rutting

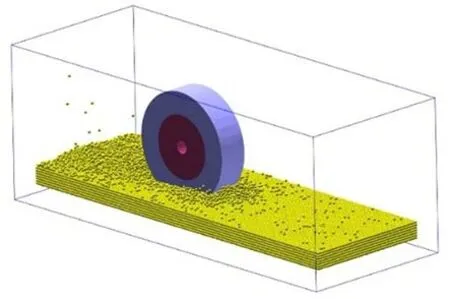
图10 T2 车辙Fig.10 T2 rutting

图11 为车轮速度时程图，从图中可以看出，在施加动态切应力后，T1、T2 中车轮开始转动，其转动速度与平动速度逐渐升高，而后趋于稳定。

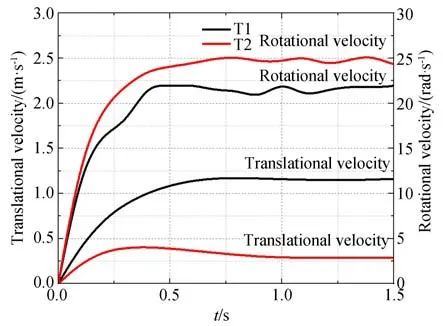
图11 车轮速度时程图Fig.11 Wheel speed-time diagram

其中，T1 转动速度稳定值约为21.05 rad·s-1，T2 转动速度稳定值约为23.39 rad·s-1，其对应转动线速度分别为9.00 m·s-1，10.00 m·s-1；T1 平动速度稳定值约为1.15 m·s-1，T2 平动速度稳定值约为0.28 m·s-1。

光面车轮由于其表面光滑，与地面滑动摩擦力较小，故在转动过程中，其转动速度略高于花纹车轮，车轮与地面相对运动时发生打滑现象，故其通行能力远低于花纹车轮。在T1 中，花纹车轮平动速度与其线速度之比约为12.78%；T2中光面车轮的比值约为2.80%。根据该比值可看出，在软土路面行驶过程中，相较于光面车轮，花纹车轮通行能力更好，由此说明了在汽车制造设计中轮胎胎面合理设计的必要性。

如图12 为系统动能时程图，从图中可以看到T1 与T2 中整个系统动能在0～0.50 s 内均持续上升，但T2 动能增长速度明显高于T1，这是因为T2 中的光面轮胎由于其与地面滑动摩擦力小，导致其转动速度高于T1 中的花纹车轮。故在此期间T2 动能增长速度高于T1。在0.50 s之后，T1、T2 系统动能均趋于稳定，其稳定值分别约为6 000 J、10 000 J。之所以出现这种差异是因为在此过程中，光面车轮相较于花纹车轮，其下陷深度更大，故在此过程中，车轮转动所引起的颗粒流动现象更为剧烈，运动颗粒范围较T1 更大，因此T2 系统动能大于T1。由此可见，车轮下陷程度也是影响车辆在软土路面通行能力的重要因素之一。

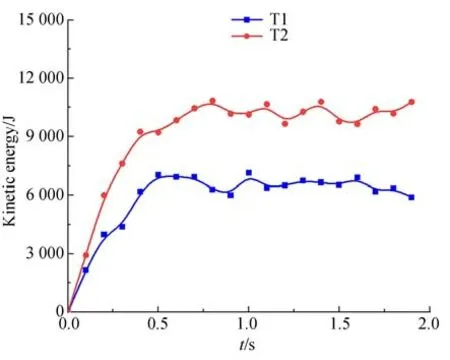
图12 动能时程图Fig.12 Kinetic energy time history

图13 和 图14 分别为T1、T2 在Y方向的位移云图。从图中可以看出，两组工况中由于车轮前进，在车轮后方产生了颗粒向后流动的现象：在t=1.00 s 时，T1 车轮后产生颗粒后移现象，其位移大小约为0.70 m；T2 约为0.40 m。

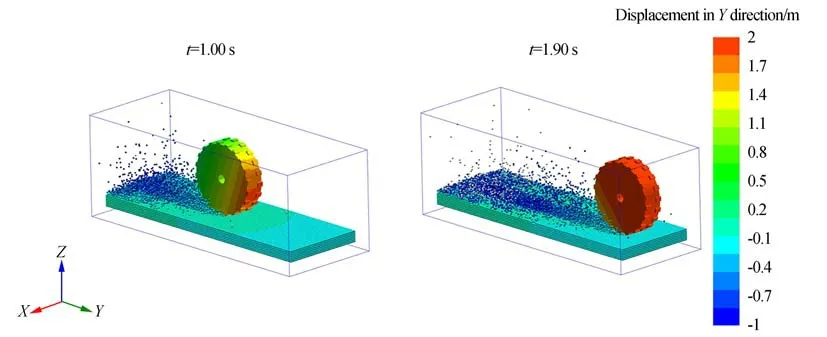
图13 T1Y方向位移云图Fig.13 Displacement cloud diagram of T1 onYdirection

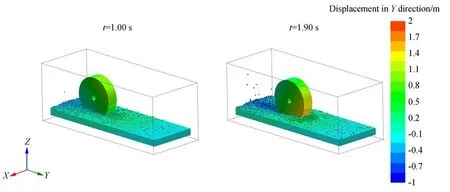
图14 T2Y方向位移云图Fig.14 Displacement cloud diagram of T2 onYdirection

在t=1.90 s 计算完毕时，T1 位移大小约为0.85 m；T2 约为0.55 m。不难看出，T1 中在花纹车轮作用下颗粒后移数值较大，在图中也可看出在T1 中发生了较为明显的颗粒飞溅现象（软土路面行驶出现尘土飞扬）。由此也可说明在软土路面中，花纹车轮相较于光面车轮转动会产生较为明显的软土后移现象从而产生软土堆积，驱动车轮向前运动，由此提高了车轮通行能力。

在图9 和图10 中可以看到，随着车轮在软土路面的运行，车轮下陷深度出现明显差异，花纹车轮下陷深度低于光面车轮，如图15 为车轮下陷深度时程图。

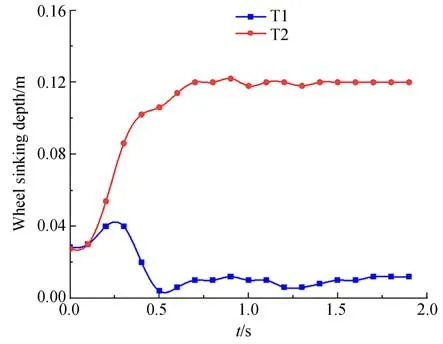
图15 车轮下陷深度时程图Fig.15 Time history of wheel sinking depth

从图中可以看出，T1 中花纹车轮随着时间的推进，在0～0.50 s 中，其下陷深度先升高后降低，之后在0.50 s 时车轮下陷深度约为0.01 m，之后便稳定于该值；T2 中光面车轮在0～0.75 s内下陷深度不断增大，在达到0.12 m 后稳定于该值。由此可见，在质量相同的情况下，花纹车轮的下陷深度远低于光面车轮。故合理地进行车轮轮胎胎面设计，可以减小车轮侵入软土路面的深度，提高通行能力。

4.2 含路障路面探究

为探究车轮在含路障路面的通行能力，设置三组路障，路障高度分别为0.02 m，0.05 m，0.07 m，记三种工况分别为U1、U2、U3，图16 为三种路障示意图。

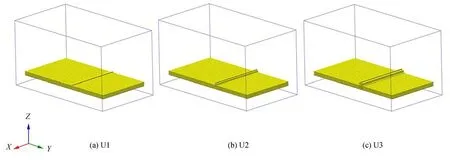
图16 路障示意图Fig.16 Schematic diagram of roadblock

花纹车轮在三种工况中行驶1 s，最终在U1、U2、U3 的行驶距离分别为1.04 m，0.96 m，0.95 m。U1 工况通行距离高于后两种工况，U2、U3通行距离相近。

图17 为在路障工况下的系统动能时程图，从图中可以看出随着时间的推移，三种工况动能逐渐上升。

图17 路障工况下动能时程图Fig.17 Kinetic energy time history under roadblock condition

与T1、T2 工况中动能随着时间的推移趋于稳定不同，U1、U2、U3 在0.5 s 后动能值出现明显波动。三种工况动能均出现先升高后下降的趋势：U1、U2、U3 均大约在0.8 s 时达到峰值，此时U1、U2、U3 的动能分别 为7 815.11 J、9341.75 J、9 822.38 J。说明在此过程中，车轮遇到障碍，必须增大制动力才能通过，由此动能上升，在通过障碍物后，动能逐渐下降。软土障碍越大，其所需能量越大，持续时间越长。

由此可见车辆在含路障路面行驶的过程中，面对障碍物需要增强制动力以通过障碍物，也要在通过障碍物后适当减速以保持车辆平稳通过。

5 力学机理探究

综合以上计算结果可知，花纹轮胎由于其胎面表面凹凸不平，增大了与软土路面的接触面积，从而增大了滑动摩擦力，故花纹车轮转速低于光面车轮。但由于胎面花纹的存在，使花纹车轮产生切向作用力，在一定程度上增大了花纹车轮的驱动力，故花纹车轮不会发生如光面车轮“打滑下陷”的现象，而是保持匀速前进。光面车轮由于驱动力不足无法顺利通行，其平动速度低于花纹车轮，但其转动速度较高，与颗粒发生较为剧烈的相对运动，从而导致软土路面松软，故其下陷深度远高于花纹车轮。相同时间内，花纹车轮通行路程更远，通行能力更强；车轮在含路障路面行驶时，往往会有坡度高低不同的路障，在车轮通过路面障碍时，车辆需要增强驱动力以获取足够能量跨越障碍物，尤其是起伏程度较大的路障，其所需能量往往更大。在车轮通过障碍物后其能耗又会有所下降，这就需要车辆在行驶过程中进行合理制动从而平稳通过。

6 结论

为了准确刻画车轮在软土路面上转动、摩擦、前行的动力学行为，提出了CDEM-DEM 耦合的数值计算方法，实现了通过施加局部坐标系下动态切向面力间接实现动态转矩施加的方法，探讨了车轮花纹、路障对车轮前行速率及能耗的影响规律。研究结果表明：

（1）花纹轮胎、光面轮胎均在软土路面留下了清晰可见的车辙；相同质量下，花纹车轮下陷深度远低于光面车轮下陷深度。

（2）花纹车轮与光面车轮在转动前行时均会产生较为明显的软土后移现象，其软土后移值分别为0.85 m、0.55 m。

（3）在相同扭矩情况下，光面车轮转速更快，并出现了打滑前行的现象；相反，花纹车轮的转速较慢，但在软土路面上却以较高的速度前行；花纹车轮平动速度与其线速度之比约为12.78%；而光面车轮比值仅为2.80%。

（4）轮胎在含路障路面通行时，其地面起伏程度越大，所消耗的能量越大。这就要求汽车在软土路面行驶时，应对于路况的不同做出合理的制动以平稳通过。