设计力求“四重” 实施要求“四明”
——谈四年级课后服务学习素材的研发
浙江杭州市萧山区银河实验小学(311202) 钟荷娟
在“双减”背景下,为真正做到“全覆盖、广参与”,提升学生的“四明”能力和智能水平,笔者自2021 年秋季开始用微课题的方式启动了“四重”“四明”课题,让学生在课后服务的“双实”(实践、实验)过程中实现“双创”(创造、创新)。笔者基于四年级数学教材,采用了设计要求“四重”、实施具有“四明”的课后服务学习素材,收到了较理想的效果。
一、重组综合性强的素材,使学生明确学习目标
选择和设计生活化的综合性素材,让学生在交流、自我发展上培养能力。
1.用故事引入
播放动画,并讲述曹冲称象的故事。三国时期,有人送给曹操一头大象,这头大象又高又大还很重。人们都在议论这头大象究竟有多重。曹操问大伙儿:“谁能想办法称出这头大象的体重?”大伙儿都答不出来,但他七岁的儿子曹冲却想出了一个好办法……”
2.用问题引发思考
向学生提出问题:
(1)曹冲思考问题时注意到了当时没有秤能称出大象的体重,转而想到用石头来代替大象的体重,这是动脑的结果吗?
(2)有人提议将大象分割后称重,这可以吗?
(3)曹冲的办法很好,还有其他办法吗?
3.学习经典样例
当笔者讲述曹冲称象这个故事时,学生都夸曹冲聪明,这时,一名平时不怎么发言的学生举手说:“老师,我认为曹冲的办法不是最好的,曹操手下有很多士兵,为什么要搬运石头这么麻烦,让士兵站上船就可以了。”
这名学生说完后,笔者称赞道:“你们认为他说的有道理吗?他的办法比曹冲的办法更方便,大家应该为他的想象力和创造力鼓掌。”
4.领悟经典样例的应用
笔者带领学生一起小结,笔者说:“刚才这名同学的发言告诉我们,只有拥有超凡的想象力,才会有一定的创造力。”
之后,笔者出了一道思考题:“有一只小猫很好动,小阳想称出它有多重,几次把猫放在秤上,但每次小猫都使劲逃脱。你有办法称出小猫的体重吗?请你说出你的方法。”学生分小组讨论,最后得出结果。
人的大脑和双手仍然是重要的学习工具,只有它们共同参与和通力合作,学生才能达到最佳的学习效果。
二、重塑自主学习的认识结构,令学生明白学习方法
在课后服务中,笔者遵循学生的认知规律,提倡“学习真知识,练就真本领”,要在“真”上下功夫,激发学生的主动性,培养探究的真方法、真功夫。
如何让学生在头脑当中将图形和算式结合起来,并进行深度思考呢?笔者设计了实践课题——观察思考。
1.“燃”大脑,细观察
笔者向学生出示如图1 所示的点子图,并提问:“观察点子图的前两行与最后一行,然后列出合理的算式。”
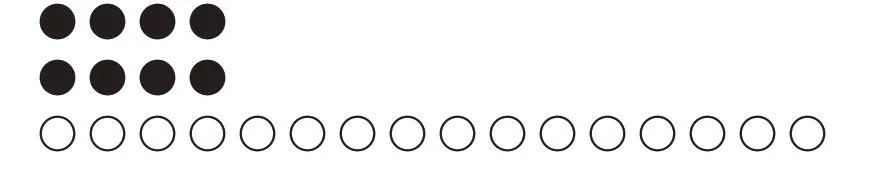
图1 点子图
学生的答案有4+4+16=24、4×2+16=24,笔者接着说:“两个算式都对。接下来啊,老师要变魔术了,你们要看仔细哦!”然后笔者用课件演示点子图的变化过程,变化后的点子图如图2所示。

图2 变化后的点子图
学生总结出:“把最下面的16个点子从长长的一行变成四行(4个一行),这样一来,就变成了六行(4个一行),也就是6个4,4×6=24。”
【教学感悟】开始阶段,帮助学生巩固对乘法意义的理解。在此基础上,借助课件演示,将抽象的算式转化为具象的图示,鼓励学生积极思考,使学生明白4×2+16=( )×4,突破了教学难点,为后面的教学做铺垫。
2.触神经,悟推理
注意是通过一些脑区的神经网络活动来实现的,注意的神经网络包括引起对问题的警觉、明确解决问题的朝向、在执行任务中保持警觉。因此,笔者注重让学生对竖式进行深度思考。
笔者出示如图3 所示的竖式问题,并提问:“现在请同学们来看一个有趣的竖式,你们发现了什么?”

图3 竖式问题
有学生猜测说:“老师,我认为三角形一定小于5。”有学生:“答案是4。”
笔者出示与竖式问题相关的点子图,如图4所示,并问:“对照点子图,4+4=8、4-4=0、4×4=16、4÷4=1分别对应哪个部分?”

图4 点子图
学生讨论后得出:4×4=16就是左下方的黑色方阵,4÷4=1 就是右上方那个灰色点子,两组白色的点子就是4+4=8,4-4=0是没有点子。
【教学感悟】学生是第一次接触这种竖式,因此笔者要先引导学生集体审题、讨论,明确思考的方向,在此基础上,鼓励学生独立思考,合作交流。在探讨的过程中,笔者鼓励学生发表不同的见解,进而优化解决问题的方案。最后,笔者借助课件演示,呈现每个算式所对应的点子图,帮助学生理解数和式的整合、变化原理,为进一步学习和丰富思维奠定基础。
3.激思维,找规律
学习不是一潭死水,而是涓涓细流。教师应引导学生在学习中不断拓展、不断创新,在拓展中不断转化、不断变形。在学生根据竖式和点子图发现“4+4=8、4×4=16、4÷4=1,总和是25,它是5 的平方”后,笔者再次出示总数不等的点子图,如图5 所示,激发学生的创新意识。
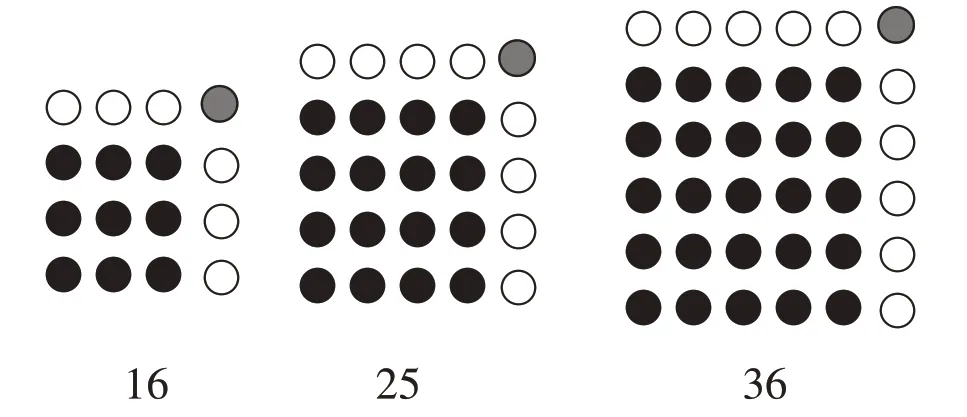
图5 总数不等的点子图
学生观察后发现,各点子图都是一个a×a的方阵,竖式中的总和对应着点子图下方的数字,竖式中△=a-1。
【教学感悟】图像表征可以帮助学生直观理解竖式模型,以“竖式—点子图”数形结合的方式,给予数的知识以几何直观,激活学生思维。
4.触发展,喜创新
笔者出示一个新的竖式问题(如图6)并说:“我这儿还有一个竖式,你们发现这两个竖式的区别了吗?”
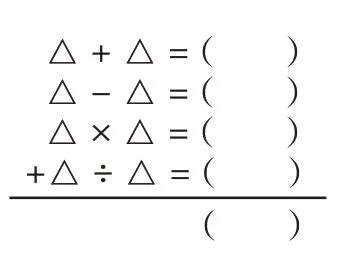
图6 竖式问题
学生发现少了最后的和,笔者引导学生:“根据前面学习的经验,你觉得和会是多少呢?为什么?”有学生说:“有可能是49、64、81 等,根据刚才竖式与点子图之间的关系,我们知道竖式中四个算式结果之和一定是一个平方数,像刚才的16、25、36 都是平方数。因此我想49、64、81 这些平方数也可能是这里的和。”
【教学感悟】好的情境是学生学习的“承重墙”。它为学生提供学习资源和活动线索,帮助学生加深概念理解,体会数学本质。本环节引入点子图,吸引了学生的眼球,在复习乘法意义的同时,激发学生探索新知的兴趣,为后面的学习做铺垫。在呈现趣味竖式时,笔者结合点子图让更多的学生能够在课堂学习的时间里有效思考和参与讨论。首先,通过小组合作,让学生初步形成解题策略,并不断优化解题思路。然后,借助点子图与竖式的关系,引导学生在观察、发现、反思中不断发现规律,让学生在这样的过程中掌握问题解决的经验和技能,使学生真正学会举一反三。最后,让学生进行竖式的水平应用和拓展设计练习,使不同水平的学生获得不同的发展。
三、重构动手操作的学习风格,促进学生明确重点难点
在学生学习了人教版四年级上册“大数的认识”内容之后,笔者先让学生查阅“世界屋脊”珠穆朗玛峰的高度,查得约8844 米,又拿出一张薄纸,设计了一场“薄纸与珠峰”的拟人对话。
薄纸小弟:大哥你好,我是薄纸小弟,今天我想告诉你,我虽然只有0.5毫米的厚度,但是我对折约30次后,就会超过你的身高。
珠峰大哥:你别胡闹了,你这么薄,别说对折30次,就是对折3000次、30000次,你也高不过我。
笔者在引出薄纸小弟与珠峰大哥的对话后,让学生动手折纸。有学生发现,纸张对折五六次后就没办法继续对折了。这时有几名学生就建议直接用计算来代替折叠,他们计算后发现,对折24 次后纸张的厚度就已经接近珠峰高度。动手操作后,学生都惊呆了:“真是不可思议,不折不知道,折后才知道。”
【教学感悟】这是一个带着问题操作的实践过程,过程中有争论、分析以及反思,真可谓是“燃”动了学生的脑力,提高了学习的效率。对教师来说,设计能触动学生大脑神经的素材至关重要。在这节课后服务中,笔者深切体会到只有让学生有深切的“感觉”,才能让学生真正“悟在其中”,有所收获。
四、重开“双创”的智慧大门,让学生明了学习过程
为开动学生大脑思维、提升学生智能而教,这是笔者研发课后服务学习素材的主旨。依赖于经典问题,笔者设计了“名著页码”活动。活动重新开启每个学生的“双创”(创造性发现和创新性发展),在课后服务中重视学生的自我反思、自我感悟与领会。
1.生活事例引入
为了标明书的页码,在排版时需要用许多数码铅字,如为了标明10页的书,就需要用11个数码铅字(其中数字10需要用两个数码铅字1和0)。
2.提出问题
(1)已知一本书的页码一共用了3001 个铅字,你知道这本书有多少页吗?
(2)一本书,印刷厂排出它的全部页码要用1392个铅字,这本书一共有多少页?
(3)名著《隋唐演义》一共有202 个页码,那编页码时要用到多少个铅字0?
(4)一本科幻小说一共131 页,共用了多少个铅字?铅字1在页码中出现了多少次?
(5)排一本辞典的页码共用了2925 个铅字,请你算一下,这本辞典有多少页?
3.问题延伸
(1)有一本48 页的书,中间缺了一张,小明将残书的页码相加,得到1131。老师说小明算错了,你知道为什么吗?
(2)“小明把一个书签夹在课本的第25、26 页之间”,这句话是正确的还是错误的?为什么?
【教学感悟】培养学生的终极目标是让学生学会学习。反观笔者过去的课堂教学,大多是照本宣科,很少设计学生喜欢的学习素材。通过实践笔者明白了,学生的学习积极性、对综合课程的喜欢程度要靠教师的引领,且学生的“双创”能力是无穷的且是可深挖的。
综上所述,数学课后服务要做到三点:变传授知识为发现知识,变厌学数学为乐在其中,拓宽学习视野。教师精心设计教学,可使课后服务的内容和方法丰富课本以外的知识体系和能力范围,由知识点扩展到知识面,使学生学习兴趣浓厚、自信满满,学习的成功感倍增,学习能力迅速提升。

