卷积神经网络在风洞天平静态校准中的应用

汪运鹏，聂少军，王 粤，姜宗林

(1.中国科学院力学研究所 高温气体动力学国家重点实验室，北京 100190；2.中国科学院大学 工程科学学院，北京 100049)

0 引言

为进一步提高航空、航天飞行器的气动性能风洞试验数据测量精准度，需要切实提高风洞天平的性能指标和测试环境适应性。风洞天平各项技术需要不断得到创新发展，尤其是在天平校准方面，需要针对安装定位、校准方法、数据采集和处理等相关技术开展持续研究，以提高风洞天平的测量性能。

风洞天平的校准可分为静态校准和动态校准，本文探讨的校准技术主要针对静态校准技术。静态校准是根据天平静态校测原理，利用天平静态校准设备（一般称为校准台或校准系统），按照静态校准方法，建立天平输出信号与所受气动载荷之间的映射关系的过程，即获取天平公式和天平其他性能参数（如精、准度指标）的过程。由于静态校准直接决定了校测效率及天平公式的准确性，关系到风洞天平在测量中获得的气动数据的精准度，所以风洞天平静态校准被认为是天平设计过程中的最重要环节[1]。风洞天平作为一类特殊的力计量传感器，在国际上还未建立统一的标定标准[2]。因此，同一台待校准的风洞天平，当采用不同校准台和不同的校准方法进行标定时，所得到的天平公式系数存在一定差异，且直接影响测量结果的不确定度。目前普遍采用线性插值拟合的方法（如最小二乘法）获取天平公式系数[3]，但是多分量风洞天平的各个分量间存在相互干扰，并且通常二次干扰和组合干扰会出现非线性特性，采用线性拟合方法会产生一定误差[4]，使得风洞天平静态校准性能因受到数据处理方法（线性拟合）的局限而较难进一步提高。

人工智能领域中的神经网络，具有很强的非线性映射及泛化功能，能较好描述非线性系统和不确定系统。早期的神经网络（如BP 算法）在函数逼近、多维插值、模式识别等领域得到广泛应用[5]。由此，一些相关拓展应用也在系统辨识、传感器非线性修正、传感器校准等方面得到了诸多探索性开展。特别是对于测力传感器校准，一方面其输出特性大都具有非线性特征，另一方面受到各种环境参数影响导致校准中存在多种误差因素。汪晓东等[6]把BP 算法用于传感器静态误差的综合修正，并论证了该神经网络方法应用的可行性。于振等[7]设计开发了一套扭矩传感器静态校准系统，同样采用BP 神经网络建立了待校准传感器测量载荷与更高精度传感器测量载荷之间的数学模型，有效提高了扭矩传感器静态校准系统的精度和可靠性。车兵辉等[4]采用具有6 个输入节点和6 个输出节点的三层BP 神经网络算法对风洞天平校准数据处理开展了相关研究。该神经网络建模方法得到的结果使拟合精度平均提高超过60%，同时有效消除了系统非线性引起的误差。

显然，具有较强非线性映射能力的BP 神经网络在数据建模方面表现出了较好的效果。但BP 神经网络也具有一定局限性，如：由于BP 神经网络在样本训练中的稳定性受到学习效率制约，导致训练效率较低；针对非线性可分问题时，BP 神经网络则可能出现局部最小值，从而导致较难得到全局最优解，且在面对大样本数据时，均方根误差（MSE）过大使得训练过程很难收敛。事实上，目前人工智能技术依然面临着许多根本性的问题，如采用不同神经网络方法对非线性函数做拟合处理，得到结果的合理性、可靠性无法给出完备验证，对深度学习训练结果的生成逻辑和认知行为无法完全理解和解释。因此，这要求我们需要根据神经网络技术的不断创新发展，研究和验证不同网络技术手段的有效性，以满足现阶段的相关测试应用。

近几年，随着人工智能技术在诸多领域的成功应用，深度学习方法获得了飞速发展。其中，卷积神经网络（convolutional neural network,CNN）在多个领域（如图像和语言的辨识处理等）得到了空前的发展和应用。作为一类包含卷积计算且具有深度结构的神经网络，卷积层的权值共享使网络中可训练的参数变少，降低了网络模型复杂度，减少过拟合，从而获得了更好的泛化能力。

本文拟在天平静态校准数据处理过程中，采用深度学习卷积神经网络方法，对多分量天平公式拟合方法进行研究。希望通过深度学习技术的引入，积极探索人工智能技术在风洞天平测试领域的有效应用。

1 风洞天平传统静态校准方法与设备

20 世纪40 年代起，风洞天平静态校准陆续从单分量人工加载砝码校准台发展到六分量自动校准设备（系统），现今已经逐步形成了风洞天平校准通用的硬件装置和逻辑方法[2]。

1.1 传统天平校准公式拟合方法

一台n分量天平安装在校准设备上后，对其进行m组加载（通常采用砝码），得到一组所施加载荷和对应的电压输出值。设Fij(i=1，···，n；j=1，···，m)为加载的载荷，ΔVij(i=1，···，n；j=1，···，m)为输出电压值。对于一台六分量天平的校准，取n=6、m=144，则可获得法向力Y单元含27 个未知变量的144 个方程的线性方程组[8]：

同理类推，可列出俯仰力矩Mz、滚转力矩Mx、轴向力X、侧向力Z、偏航力矩My的线性方程组。分别对这六个线性方程组求解，即可得到天平校准公式的各个系数[8]。

分析这六个线性方程组有如下的共同点：均为具有27 个未知变量和144 个方程的线性方程组。方程组的个数大于未知变量的个数，超过了一般所需要的定解条件，这类方程为超定方程，是一个矛盾方程组。从实际出发，通常采用最小二乘法求出它的最小二乘解[9]，这便是传统天平校准过程中的数据处理方法。这种方法在一定条件要求下是有效的，可以解决工程中的实际问题。

1.2 超大量程风洞天平校准系统AiBCS

基于脉冲风洞的测力天平量程特点，中国科学院力学研究所建成了一台超大载荷风洞天平高精度全自动校准系统（AiBCS），见图1[10]。该系统采用体轴坐标系校准方法，即，在风洞天平受载荷变形后，可实现回零式自动补偿，使天平恢复到初始状态，从而保持施加力和力矩的方向始终与天平体轴坐标系保持一致。

图1 AiBCS 校准系统照片[10]Fig.1 The photo of AiBCS[10]

AiBCS 设计载荷指标充分考虑了多个因素，如高超飞行器升阻比特点、激波风洞流场起动特点[11]等。AiBCS 校准精度指标优于0.05%FS（full scale，指在最大测量范围中的百分占比），可实现最大法向力±15 kN 量程范围的脉冲型天平的高精确度“一键式”全自动校准[10]。

2 神经网络方法在天平静校中应用的技术问题探讨

首先，风洞天平校准设备按照加载坐标轴系的不同，可分为体轴系天平校准设备和地轴系天平校准设备。对于地轴系校准台，施加载荷的方向假设与地轴系一致，对天平受载后产生的变形不作调整。为了提高天平静校的准确度，一般通过测量天平受载后产生的变形量，对施加载荷进行坐标轴系修正，获得近似于在体轴系天平校准设备上的结果。对于体轴系校准设备而言，其施加载荷方向始终与天平体轴系一致，从而保证校准加载过程与实际风洞测试受载过程基本一致。因此，相较于地轴系设备，其具有更高的校准精准度。体轴系校准台也大致分为两类，补偿型和非补偿型设备。补偿型体轴系天平校准设备结构复杂、造价高，但是其校准得到的天平公式中，干扰项数量明显减少，干扰量也明显降低，精准度提高。非补偿型校准台虽然具有设备结构简化、不需调整系统的优点，但是该类型设备不考虑施加载荷方向随天平受载变形后的变化，会引入一定误差，相对降低了校测精准度。通过地轴系与体轴系设备校准差别的对比，显然补偿型体轴系天平校准台具有更高的校准性能。原因是天平受载变形后，该类型设备可实时跟踪测量变形量大小并换算复位量，使得施加载荷方向与天平体轴系一致，即，其可自动调整加载系统，保证天平加载状态不变[8]。

其次，天平系统刚度不足等因素会增加非线性和交叉项干扰，使得天平校准复杂化，传统的多项式拟合方法无法处理这种非线性干扰[12]。神经网络方法是一种模拟人脑的神经网络，以期能够实现类人工智能的机器学习技术。该技术目前已经在诸多领域广泛开展了应用研究，包括风洞测试中测力天平技术的智能化探索等[13]。神经网络建模方法的优点是可以更好地消除天平分量间非线性干扰引起的误差。将神经网络模型（如人工神经网络、卷积神经网络等）应用于天平静态校准数据处理，主要是通过对加载数据开展训练建模，得到校准模型，代替基于最小二乘多项式拟合方法得到的传统天平校准公式。

但同时也应注意到，神经网络方法是对一组输入信号和一组输出信号之间的映射关系进行建模，通过调整内部大量节点（神经元）之间相互连接的权重，从而达到处理信息的目的。作为一种黑箱方法，它不会给出模型处理过程和内部解算机制，这意味着如果天平校准状态（加载过程）与天平使用状态（应用受载过程）不一致，那么由于不一致而产生的误差将被无条件地作为“有效”信息增加到训练模型中。因此，前面讨论的地轴系设备运行中，如果采用神经网络方法对校准数据进行处理建模，那么加载载荷方向与天平体轴系的不一致问题所导致的误差量将被包含在建模信息中处理。早期部分天平校准台不具备天平校准回零功能，国内外一些技术研究人员也采用了一些修正措施[14-15]，因此一些地轴系天平校准台也可以实现体轴系静态校准，但前提条件是对校准结果要进行准确评估并满足使用要求。

综上所述，针对神经网络方法在天平静态校准中的有效应用，天平建模所需样本数据应满足施加载荷方向与天平体轴坐标系一致的条件。

3 基于CNN 的天平校准数据处理方法

3.1 卷积神经网络

对于一般的人工智能任务而言，提取特征是其中重要且困难的关键步骤。传统的机器学习算法通过人工的方式设计有效的特征集合，当问题比较复杂时，需要花费研究人员大量的时间和精力，而且实际问题中的不确定因素会导致提取的特征效果不理想，甚至无法有效提取特征。相比于传统的机器学习算法，深度学习算法会自动提取问题的简单特征，通过学习特征与任务之间的关联，逐渐将各层简单特征组合成能反映任务的复杂特征，从而使整个问题变得简单且有效。深度学习方法由于其学习和适应能力强、可移植性好且所需样本量小等优点，在诸多领域有着非常广泛的应用，如计算机视觉、语音识别和自然语言处理等[16]。

神经网络结构是深度学习中至关重要的部分，对神经网络模型的准确率会产生巨大的影响。CNN 是深度学习中常用的一种神经网络结构，常用于解决图像识别和回归预测等问题。

在对天平进行静态校准的过程中，天平测量输出信号与气动载荷信号具有一一映射关系，即当天平的输出值确定时，其对应的载荷值也随之确定。天平的输出信号与载荷的关系本质上是回归预测问题。CNN 在处理空间信息中具有独特的优势，在对样本数据进行监督学习后可以自动地提取天平输出信号中的关键特征，通过不断训练完成从天平输出信号到载荷信号的拟合，从而预测天平输出的载荷信号。故本研究采用基于CNN 的智能模型对天平进行静态校准训练，从而获得天平精准度和不确定度等校准性能指标。

3.2 CNN 校准模型的构建

针对一台六分量杆式应变天平在AiBCS 测量中输出的电压值和对应的载荷值，构建风洞天平静态校准数据的CNN 校准模型。在构建模型之前需要采集适量的样本，包括训练样本、验证样本和测试样本，三者在特征上应该尽可能保持一致。首先在AiBCS上采集144 组样本，将样本集随机划分为训练样本集和验证样本集，其中80%的样本作为训练样本，用于更新网络参数，剩余20%的样本作为验证样本用于进一步优化网络参数。在CNN 校准模型构建完成之后，在AiBCS 上采集适量样本作为测试样本用于校准数据分析，主要包括精度、误差以及不确定度分析。

3.2.1 卷积网络结构

CNN 校准模型包括输入层、卷积层和输出层，输入层是六分量的天平电压值和对应的载荷值；卷积层是CNN 校准模型中的核心层，其数目和大小会影响模型的训练结果，文中采用一维卷积函数；输出层是六分量天平的载荷预测值。

在CNN 校准模型的训练过程中，常用损失函数（loss）来衡量网络模型的质量。随着训练轮数的增加，不断降低损失函数的值，以更新网络参数，从而使模型达到收敛状态。CNN 校准模型采用均方误差（mean square error，MSE）函数作为损失函数，MSE 是反映模型的目标值与输出预测值的离散程度，其值越小，说明模型输出值与真实值越接近，模型质量越好。MSE 的计算公式为：

式中：N是样本总数；yi和分别是第i组样本的真实值与预测值。

CNN 校准模型训练流程如图2 所示。首先将训练样本集中天平输出的电压值和对应的载荷值作为输入层，然后通过卷积层更新模型的网络参数，当损失函数和训练轮数满足要求后，输出天平的载荷预测值，即完成CNN 校准模型的训练。

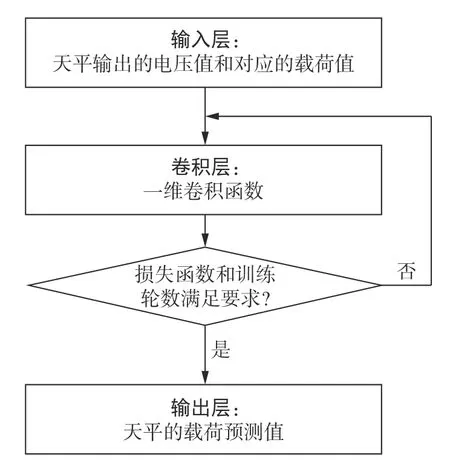
图2 CNN 校准模型训练流程图Fig.2 Flow chart of the CNN calibration model

3.2.2 参数优化问题

在确定CNN 校准模型的结构之后，需要通过验证集进一步优化神经网络参数，一般针对训练轮数和卷积层数对CNN 校准模型进行优化。优化目标是在保证模型精准度足够高的情况下，尽可能减少模型的训练时间，节省计算成本。经过分析，本文天平静校案例中的初始参数设定如下：卷积层数为4，学习率为1×10-5，训练轮数为10 000。

当其他参数不变时，一定程度上，随着训练轮数的增加，模型的损失函数会降低，训练结果的精准度会相应提高，同时计算时间也会相应增加。表1 展示的是训练轮数分别是10 000、50 000 和100 000 时的验证样本集的损失函数值。当训练轮数是10 000 时，损失函数的值由初始的1×103量级降低到1×102量级；当训练轮数增加到50 000 时，损失函数的值降低到1×10-2量级；继续增加训练轮数至100 000，此时的损失函数稳定在1×10-2量级保持不变，但计算时间明显增加。这说明在一定范围内，增加训练轮数可以有效降低损失函数值。因此，综合损失函数值与计算时间，选取训练轮数为50 000。

表1 不同训练轮数的CNN 校准模型的loss 对比Table 1 Loss of CNN calibration model with different epochs

在确定训练轮数之后，研究卷积层数对模型训练结果的影响，通过比较验证样本集的损失函数值来优化模型参数。将卷积层数由4 分别增加至8 和12，损失函数值整理如表2 所示。由表2 数据可知，当训练轮数为50 000 时，卷积层数为4、8 和12 的CNN 校准模型的最终损失函数值均能由1×103量级降低到1×10-2量级，并且最终保持稳定趋势。随着卷积层数的增加，模型结构更加复杂，相应的计算时间也会增加。因此，综合选取卷积层数为4 层。

表2 不同卷积层数的CNN 校准模型的loss 对比Table 2 Loss of CNN calibration model with different convolutional layers

综上所述，在保证最终损失函数值足够小且稳定的情况下，尽可能缩短计算时间，优化后的CNN 智能模型的卷积层数为4，训练轮数为50 000，学习率为1×10-5。

3.3 天平校准数据精准度分析

在确定CNN 校准模型的结构参数和训练参数之后，为了进一步评估训练轮数对训练结果的影响，随机选取验证样本集中的一组数据进行相对误差分析。以天平输出电压值对应的载荷值为真实值F，CNN校准模型输出的天平载荷值为预测值，计算两者的相对误差δ，计算公式为：

表3 展示的是卷积层数为4、采用不同训练轮数时，CNN 校准模型的相对误差的计算结果。由表中的数据可知，当训练轮数为10 000 时，相对误差值比较大，甚至出现了错误情况；增加训练轮数至50 000时，天平各分量的相对误差明显降低，基本在1%量级；而当训练轮数为50 000 和100 000 时，两者的相对误差比较相近，此时继续增加训练轮数并不能提升模型的精准度。

表3 不同训练轮数的CNN 校准模型的相对误差（%）对比Table 3 Relative error (%) of CNN calibration model with different epochs

表4 给出了训练轮数为50 000、采用不同卷积层数时，CNN 校准模型的相对误差的计算结果。由表中数据可以得出，当卷积层数由4 增加至8 和12 时，天平各分量的相对误差并没有明显的降低，反而出现了增加的趋势。因此，综合选取训练轮数为50 000，卷积层数为4，此时CNN 校准模型的天平各分量的相对误差基本控制在1% 以内，具有较高的精准度，且需要的计算时间相对较少。以上工作验证了该CNN 校准模型的可行性，为将该方法应用于天平静态校准提供了可靠的数据支撑。

表4 不同卷积层数的CNN 校准模型的相对误差（%）对比Table 4 Relative error (%) of CNN calibration model with different convolutional layers

4 天平校准应用及数据精准度分析

4.1 天平静态校准综合加载误差和精度

本文针对一台脉冲型六分量杆式应变天平（“S01-2 天平”，见图3）开展了静态校准应用与性能评估。该天平作为常规测力天平应用于JF-12 激波风洞气动试验，其设计载荷指标见表5。

图3 六分量脉冲型应变天平Fig.3 The six-component pulse-type strain-gauge balance

表5 天平S01-2 设计载荷Table 5 Design load of balance S01-2

采用CNN 训练的模型对天平训练样本进行处理，经过分析发现，处理后的天平各分量载荷与电压信号对应的真实载荷值之间的相对误差非常小，精准度较高。因此，尝试将该CNN 校准模型应用于天平测试样本。针对S01-2 天平在AiBCS 中采集适量测试样本，采用已优化的CNN 校准模型对测试样本进行处理，对天平静态校准综合加载误差和加载重复性等指标进行分析。

本文中的综合加载误差是指经过CNN 校准模型处理后，输出的载荷值（近似值）与所施加的载荷值（真实值）之间的标准偏差，该指标反映了测量过程中的系统误差。在实际操作中，采用CNN 校准模型对获得的天平输出电压信号进行处理，将得到的处理结果与实际载荷值进行对比，计算得到天平综合加载误差。天平综合加载误差计算公式为：

式中：W表示天平综合加载误差；Pmax表示最大设计载荷；F和P分别表示近似载荷值和真实载荷值；m表示各分量载荷的总组数；下标i和j分别表示第i分量和第j组施加载荷。

表6 中给出了经过传统天平校准公式和CNN 校准模型处理后的天平综合加载误差，并与国军标先进指标[9]进行了对比。可以发现，同一设备和仪器条件下，CNN 校准方法使得加载误差大幅度降低，最大降幅超过70%，且基本达到了国军标先进指标要求。

表6 天平综合加载误差（%FS）Table 6 Balance combining loading error (%FS)

此外，在相同的加载条件下，根据天平各个分量的设计载荷，对天平进行重复性加载，以评估测量过程中的随机误差。用于天平各分量的综合加载重复性计算的公式为：

式中：S表示天平的综合加载重复性；X和Xmax分别表示天平输出载荷值和最大设计载荷；n表示对天平分量重复性加载的次数；下标i和j分别表示第i分量和第j次重复加载。

表7 为传统天平校准公式和CNN 校准模型处理后的天平综合加载重复性对比。可见，CNN 校准模型处理得到的数据重复性指标更优，精度得到了较大幅度的提升，达到了国军标先进指标的要求。

表7 天平综合加载重复性（%FS）Table 7 Balance combining loading repeatability (%FS)

4.2 不确定度分析

对天平静态校准的不确定度进行了分析，评估校准模型得到的结果与真实载荷值之间的接近程度，同时反映测量过程中的系统误差和随机误差。

表8 为传统天平校准公式和CNN 校准模型校准结果的不确定度对比，其中k表示置信水平为95%时的包含因子。天平校准公式和CNN 校准模型的B 类不确定度（主要包括载荷源不确定度、数据采集系统引入的不确定度和校准设备引入的不确定度）保持一致，其差别主要体现在A 类不确定度（主要包括天平综合加载误差和天平综合加载重复性）中。CNN 校准模型获得的不确定度远小于天平校准公式计算得到的不确定度。基于CNN 建模的静态校准性能较传统天平公式法得到了较大幅度的提升。

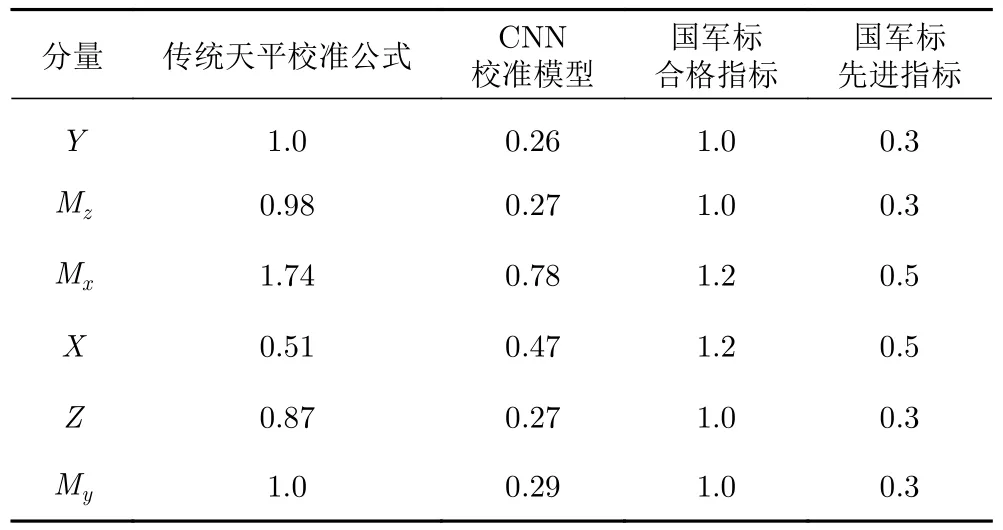
表8 天平扩展不确定度（k=2）（%FS）Table 8 Balance expanded measurement uncertainty (k=2) (%FS)

5 结论与展望

为了进一步提升应变天平静态校准性能，本文探索采用CNN 对天平校准数据进行深度学习建模处理。在引入CNN 技术之前，对神经网络技术（包括BP 神经网络、CNN 等）在风洞天平静态校准中应用的适用性条件进行了讨论。为确保天平静态校准性能，天平校准施加载荷方向应与天平体轴坐标系一致，以减小由于受载变形导致的误差。因此，采用具有体轴校准且自动复位功能的校准设备，并对采集样本数据进行CNN 方法建模，可大大提高校准性能。采用CNN 训练的校准模型获取了天平电压输出与所受载荷的高精度映射关系。数据结果显示：相较于传统公式法，CNN 校准模型得到的校准结果的综合加载误差、重复性及不确定度三项指标最大降幅达到或超过70%。CNN 校准模型对天平输出信号高阶非线性干扰的处理优于传统方法，有效降低了各个分量间的载荷干扰，体现了CNN 在天平静态校准中的有效性。人工智能深度学习技术与风洞天平校准的交叉应用具有较大的工程推广应用价值和广泛的发展前景。