非直通甲板舰船空气流场的结构化建模

李海旭，王金玲

(1.中国船舶集团有限公司 系统工程研究院，北京 100094；2.清华大学 网络科学与网络空间研究院，北京 100084)

0 引言

舰载机起降作业难度和危险系数远高于陆基起降作业，被喻为“刀尖上的舞蹈”，主要原因有三方面：一是舰船提供的起降平台尺寸很小，二是平台处于六自由度运动状态，三是舰船具有复杂的空气流场[1]。其中空气流场对舰载机起降的影响最复杂，其数学建模和力学建模过程均涉及多方面动态耦合要素，所涉及的涡流问题也是研究领域目前的难题。

舰船空气流场对舰载机起降的影响问题，解决思路主要有三类：一是通过大量的试飞和风洞试验验证每种工况条件下的空气流场是否满足起降要求，从而建立可用的起降工况图谱[2]；二是通过CFD 模拟舰船空气流场，定量分析流场对舰载机的影响[3]；三是分析空气流场的组成，通过数学模型建立流场的结构化表达。直通甲板舰船的空气流场结构被称作“公鸡尾流”，其结构化建模问题已于1980 年代得到解决，而非直通甲板舰船的空气流场结构形式更为复杂，近年来虽通过数值模拟、风洞试验或实船测量等方法开展了研究，但其结构化建模问题一直未能得到解决。

本文的研究目的是探索非直通甲板舰船的空气流场的结构化建模方法，通过对其流场结构形成机理进行分析，进而采用流场特性频域分析和数据拟合方法，解析流场的稳态、周期和随机分量，并对初步得到的结构化模型进行仿真验证。

1 舰船空气流场结构化建模必要性

通过试飞和风洞试验直接验证每种工况条件下的空气流场是否满足起降要求，实际上是绕开了对舰船空气流场自身结构问题的研究，来直接验证舰载机和舰船的配合特性。该方法在过去60 多年时间里在不同国家得到了广泛的应用。但该方法耗时、耗力、危险系数高，并且无法得到更进一步的定量流场。

流体力学仿真建模，是对空气流场结构进行直接定量模拟，具有成本小、风险低、周期短等优势[4]。20 世纪70 年代中期，美国海军提出了“人在回路”模拟器概念，来定量和定性评估流场对舰载机的影响[5]。随后，英国、加拿大、澳大利亚[6-7]等国均开始致力于机-舰动态配合（ship-helicopter dynamic interface）仿真研究，荷兰也开发了SHOL-X 仿真软件来定量模拟舰船空气流场以及分析对舰载机起降的影响。

机-舰动态配合仿真中，虽然直升机飞行动力学模型已经相对成熟，但舰船空气流场模型精度的不足严重限制了机-舰动态配合仿真模拟器在机-舰动态飞行训练和测试中的应用[6]。为了得到更精确的舰船空气流场模型，相关专家一方面不断优化流场仿真方法，另一方面利用实船测量、风洞试验不断修正舰船空气流场仿真模型。流体力学仿真建模需要建立网格进行求解计算，不能作为数学模型直接应用于机-舰动态配合实时仿真[8]。

舰船空气流场的结构化建模，则是对舰船空气流场的产生机理、基本结构、组成和强度等进行分析，并建立数学模型。该方法不仅进一步剖析了流场结构本身，也有助于深入分析流场对直升机起降的影响机理，同时在各类机-舰动态建模分析中可以作为定量数学模型参与建模分析。工程上一般根据甲板类型把舰船分为直通甲板舰船和非直通甲板舰船进行研究，其中直通甲板舰船更多的是研究舰船后方的空气流场结构；非直通甲板舰船则更多研究的是舰船尾部、飞行甲板上方的流场结构。

2 舰船空气流场结构化建模现状

2.1 直通型甲板舰船的空气流场结构化建模

直通型甲板舰船的空气流场已经实现了结构化建模。MIL-F-8785C 军用规范将直通型甲板舰船后方的气流扰动视作随机自由大气湍流（u1、v1、w1）、稳态空气尾流（u2、w2）、周期性空气尾流（u3、w3）、随机尾流（u4、v4、w4）四种分量成分的合成，并对其进行了定量描述，规定用此检验飞机在气流扰动下的着舰性能。甲板风的水平尾流ug、横向尾流vg、垂向尾流wg可按式（1）计算：

其中：稳态空气尾流是舰尾流大气扰动的主要组成部分，由甲板风与舰船结构决定；周期性尾流由船体纵摇运动产生，随舰船纵摇频率、纵揺幅值、甲板上的风环境及离舰距离而变化；自由大气湍流特性是大气自身特性，与飞机相对于舰船的位置无关；随机尾流特性由特定形式的白噪声经成形滤波器后得到。

直通甲板舰船的稳态空气尾流，呈现先下洗再上升的特点，也被称作“公鸡尾流”（如图1 所示）。

基于大量试验数据建立的美国号航母 CVA 稳态空气尾流如图2 所示。

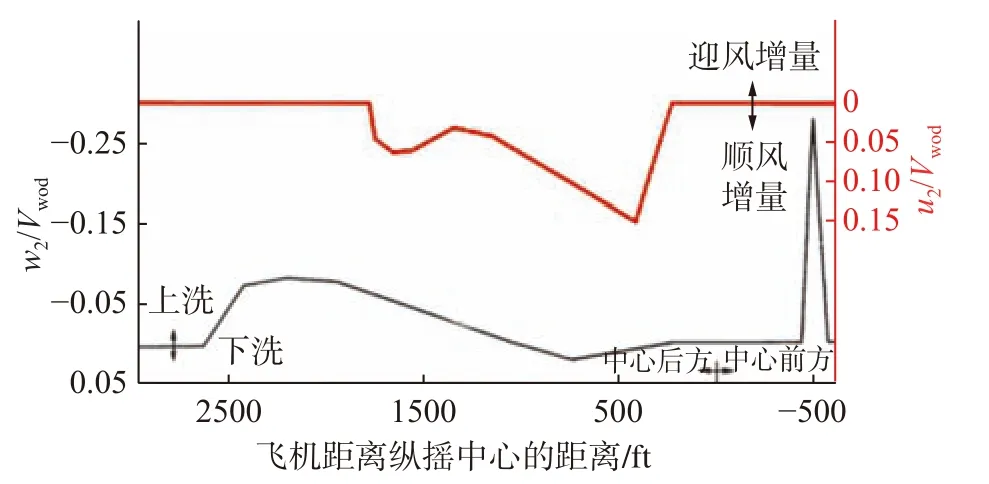
图2 CVA 舰稳态尾流分布Fig.2 Steady wake of CVA

2.2 非直通型甲板舰船的空气流场结构化建模进展

非直通甲板舰船空气流场模型的研究可以追溯到20 世纪70 年代。1977 年Fortenbaugh[9]最早基于1∶50 的FF-1052 护卫舰模型的Boeing-Vertol 风洞试验数据构建了以平均流叠加通过微分方程定义的随机流场的两分量空气流场模型。1978 年Nave[10]在此基础上进行了版本更新，利用一阶滤波和随机数插值法构建随机分量，得到了与风洞试验谱吻合良好的结果。1978～1979 年，Fortenbaugh[11]通过使用Nave 推荐的一阶滤波白噪声代替原始随机分量中的二阶噪声，并将其拓展应用于DD-963 驱逐舰，明显提高了模型的精度并降低了其复杂性。1983 年，Hanson[12]进一步将Nave 的随机数插值方案修改合并到Fortenbaugh 的DD-963 空气流场模型中，但飞行员在模拟器中体验后认为此改进的DD-963 空气流场模型湍流水平过高，需要将速度总方差减少60%～70%后才能与实际情况吻合。1994 年，澳大利亚的Erm[13]再次对上述模型进行了修订，利用自回归方程定义湍流分量，并引入加权方式进行计算，此模型被应用于SH-60/FFG-7 机-舰动态配合仿真程序中，但与实船试验结果相比仍存在明显差异。

2006 年～2012 年期间，佛罗里达大西洋大学的Gaokar 和Mohan[14-21]等致力于非直通甲板舰船空气流场模型研究，并提出了一种从流场数据库中提取尾流自相关和自谱以及互相关和互谱的解释型模型框架的方法，所提取的模型非常适合于白噪声驱动的整形滤波器的设计，但由于模型框架是基于经典湍流理论构建的，同时其未解决互谱相位问题，因此在某些情况下无法捕获自谱的峰值。

综合来说，目前非直通甲板舰船尚未建立类似直通甲板舰船的标准化空气流场结构模型。本文拟从非直通甲板舰船空气流场形成机理出发，对此进行探索研究。

3 非直通甲板舰船空气流场形成机理

已有的研究表明，舰船空气流场具有不稳定性、大分离区域特性和低速性，其是随时间和空间发生变化的[22]、存在大量拟序结构的复杂三维湍流，其中稳态分量由甲板风风向角和舰船结构共同决定，是其主要组成部分。非直通甲板舰船空气流场稳态特性的形成机理在文献[23] 中已有详细分析，前期的研究表明，舰船空气尾流场中有两种类型的分离，一种由于黏性，一种由于障碍物的尖角。前者与流动的雷诺数紧密相关，而后者纯粹是一种无黏性现象，与雷诺数没有关系，但这两种分离都产生自由涡。在舰船空气尾流场中，只在舰船表面的近壁区域内是由黏性作用产生的分离占主导地位，其他位置的分离主要属于后者[24]。舰船空气尾流场是关于雷诺数独立的，因此推测对于同一风向角只需要计算一个风速即可，其他风速的结果可通过比例缩放得到，这一现象被称为雷诺数独立性或雷诺自准准则。

本文针对瞬态流场的建模采用频谱分析结合流场结构机理进行分析，在对空气流场涡流结构和组成进行分析的基础上，通过随机取样频域谱分析，解析其稳态分量和周期性分量。对非直通甲板舰船时域流场（图3）开展频谱分析，通过傅里叶变换得到三向速度的频谱曲线（图4）。文中所有速度均为基于甲板风速的无量纲化速度，黑色曲线为通过傅里叶变换得到的三向速度频谱曲线，红色曲线是基于频谱曲线进行了函数拟合。选择瞬态流场主频率fmax、信号峰值Amax、带宽B以及噪声能量En四个特征值开展分析，频谱特性如图5 所示。

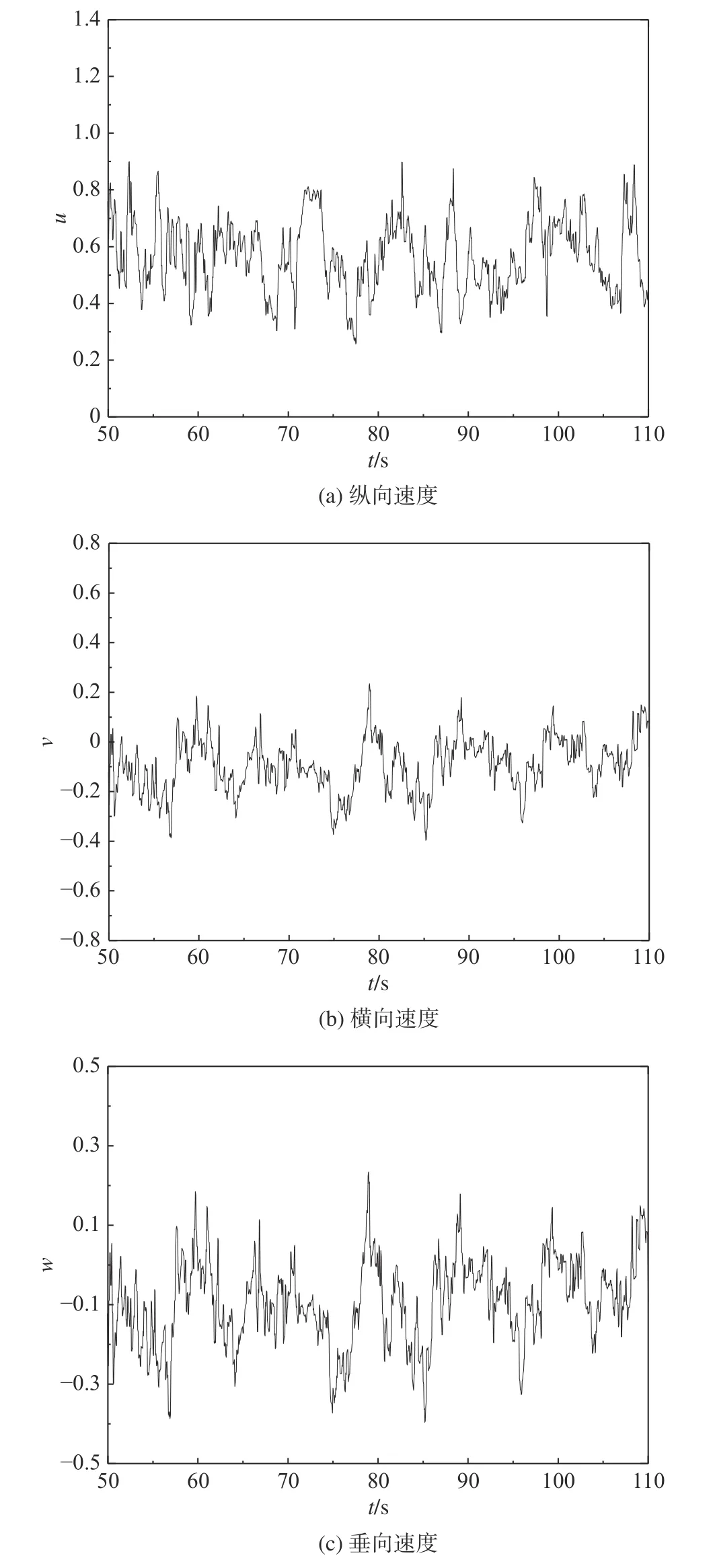
图3 三向速度时域曲线Fig.3 Temporal histories of three velocity components

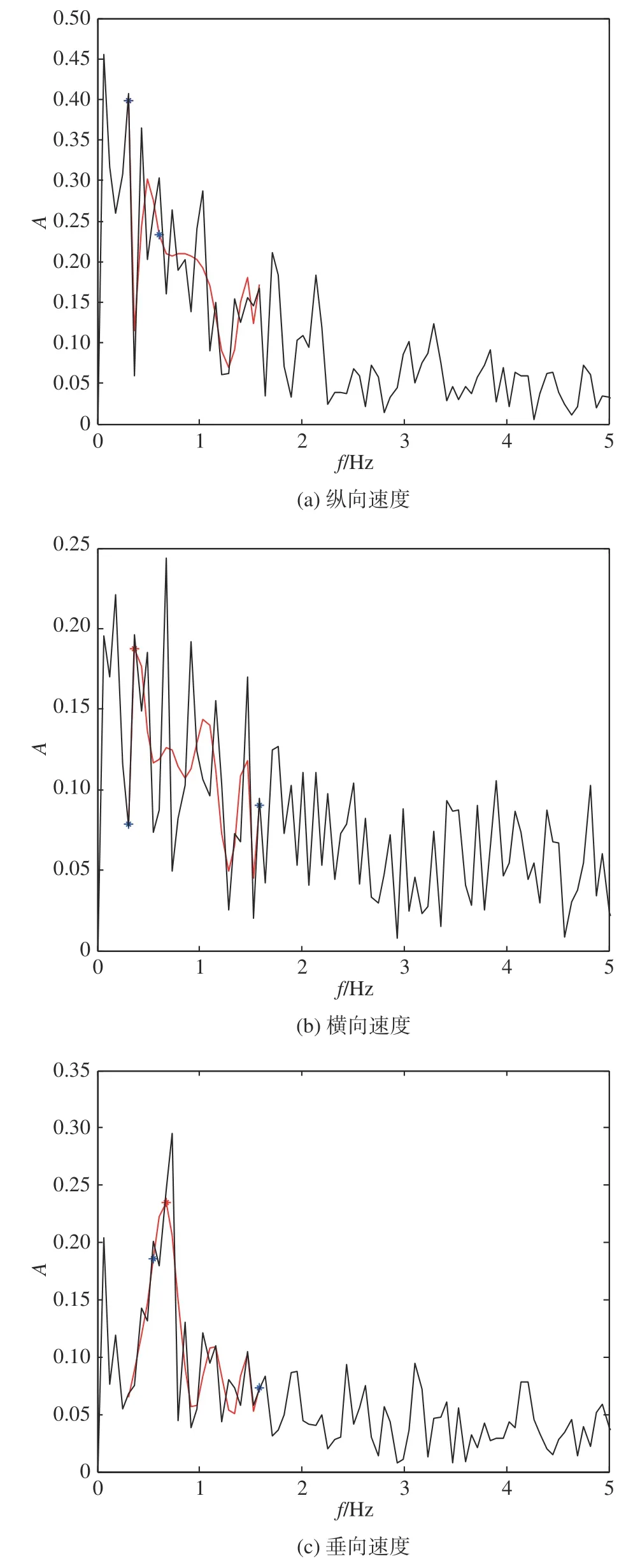
图4 三向速度频域曲线Fig.4 Frequency speatra of three velocity components

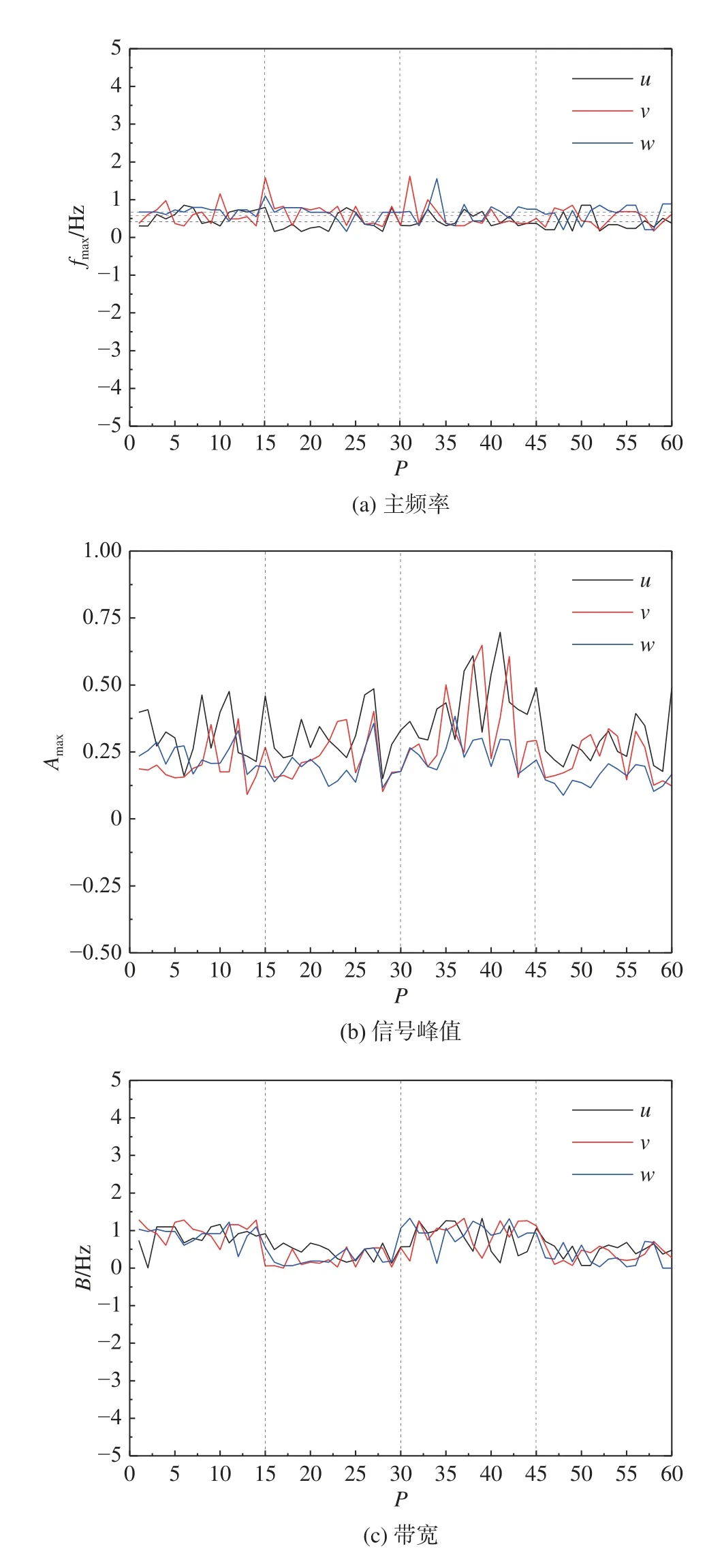
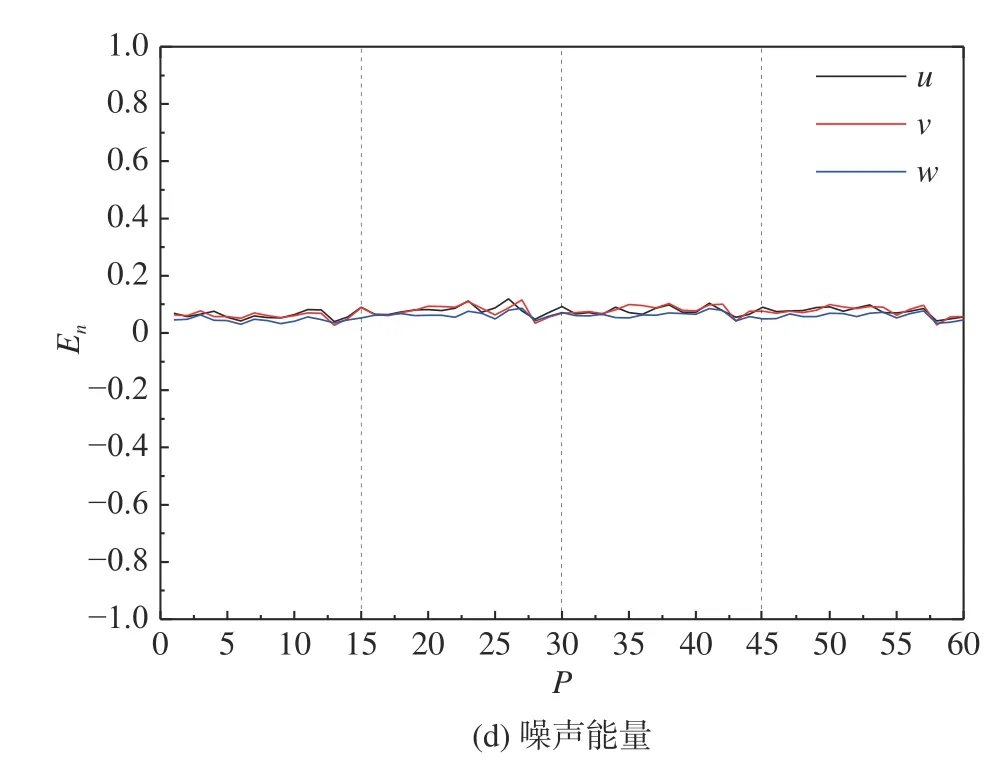
图5 频谱特性Fig.5 Spectral characteristics

结合频谱曲线及频谱特性，发现：三向速度频谱均呈低通滤波器特征，纵向速度是由主流速度决定的，与分离涡脱落周期相符，其主频处于0.2～0.5 Hz之间；横向与垂向速度的主频处于0.4～0.7 Hz 之间，与图6（图中p、q、r为船体坐标系中的横摇、纵摇、艏摇角速度分量，单位rad/s）中船体纵横摇频率相符，因此判断横向和垂向速度波动是由船体运动引起的，并定义此部分流场为周期分量。噪声能量的特点是在较大范围的频谱上能量是均匀分布的。观察频谱曲线及噪声能量分布发现，噪声能量与空间位置和速度方向无关，其大小为0.05 左右，因此判断噪声可能主要是由大气湍流和其他环境扰动产生的，并定义为随机分量。综上所述，非直通甲板舰船空气流场由稳态分量和瞬态分量构成，瞬态分量又可分解为周期分量和随机分量两部分，且稳态分量为流场的主导成分。

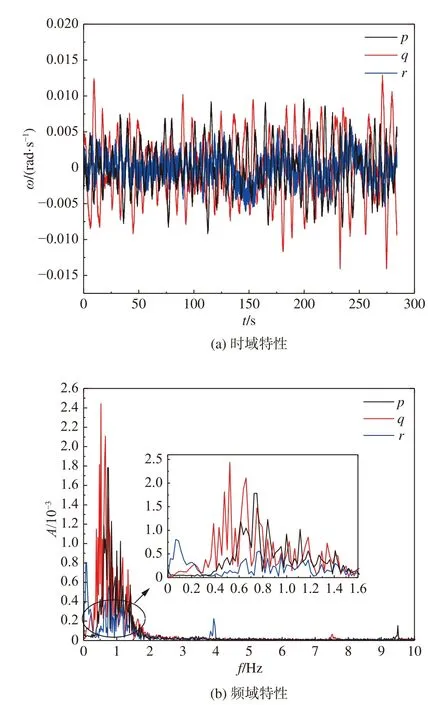
图6 船体运动特性Fig.6 Ship motion charateristics

4 非直通甲板舰船空气流场建模

本节进一步通过数据拟合方法，构建非直通甲板舰船空气流场分量模型，对非直通甲板舰船空气流场Vairwake的三部分，即稳态流场Vst、周期流场Vp、随机流场Vr，分别进行研究。

4.1 稳态流场建模与验证

稳态流场Vst（三向速度分量为U、V、W）由甲板风和舰船结构决定，可表示为：

式中：Vst为稳态流场速度矢量，m/s；Γ为与船型有关的参数；x、y、z为船体坐标系中空间坐标，m。

特定甲板风工况与特定船型组合下的稳态流场可简化为：

根据式（3），稳态模型转化为三向速度随空间坐标变化的函数问题。但在物理上，流场的分布是由船体结构和甲板风决定的，三维流场可视为二维流场的叠加，属于二次超曲面，故稳态模型进一步简化为二维曲面拟合的问题，即：

其中，（a0，a1，a2，···，a9）是二次曲面中的10 个未知量。

利用最小二乘法对稳态流场进行二次曲面拟合的参数优化，以拟合值和实测值的差方和作为优化指标：

式中：J为优化函数；为i测点的速度拟合值；Vst,i为i测点的速度测量值。

对式（5）中的各项系数求导即可得到（a0，a1，a2，···，a9）的系数矩阵M。

基于建立的稳态流场模型仿真得到的流场速度与实测结果对比见图7。结果显示，模型仿真速度与实测速度变化趋势相同，模型仿真平均误差为11.11%，速度标准差为0.10，证明了稳态模型的有效性。

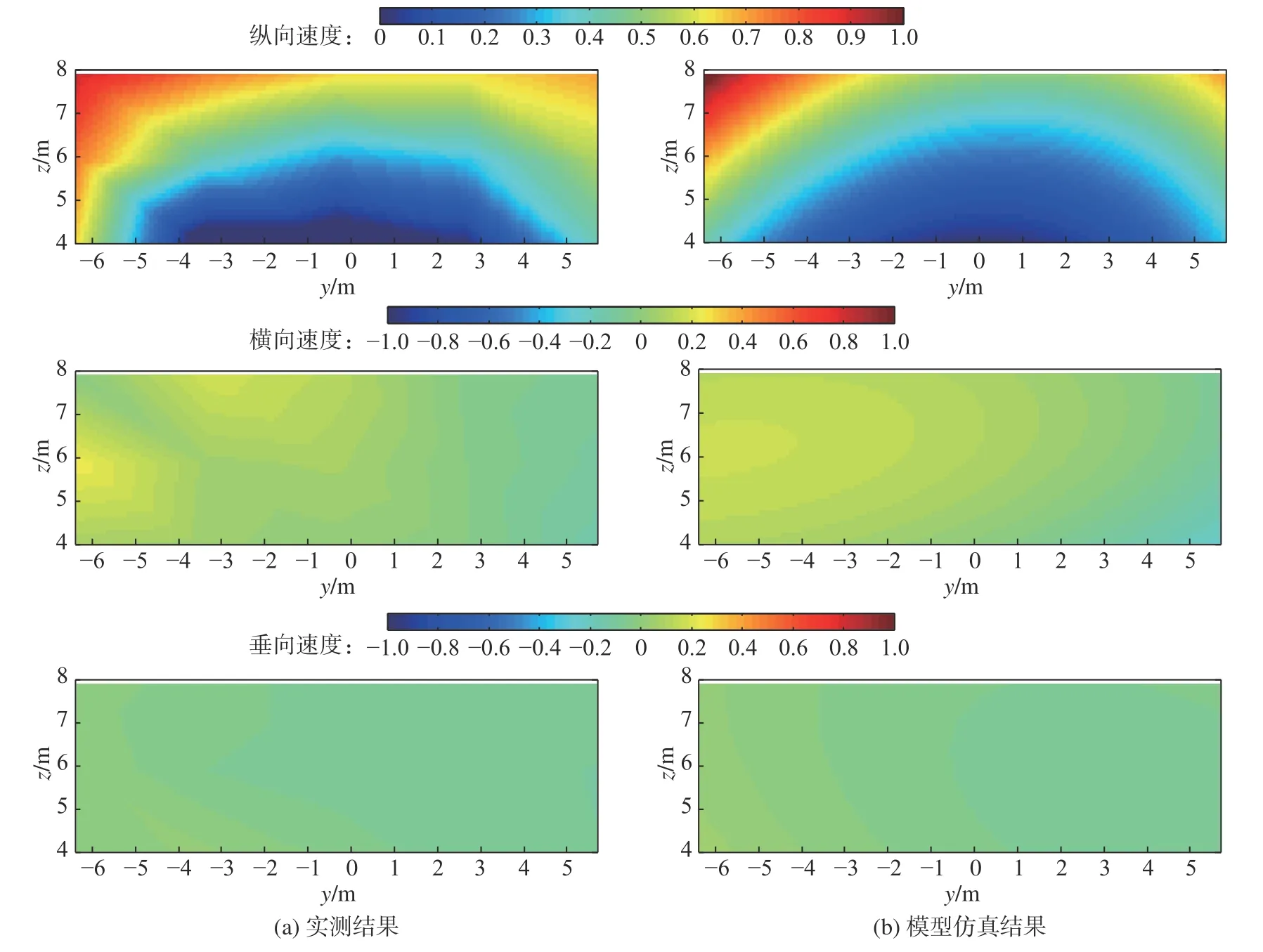
图7 三向速度云图对比Fig.7 Measured and modelled velocity contours

图8 给出了0°风向角下舰船中纵面及理想着舰点所在横向截面上的流线分布。直升机进场着舰过程中在甲板上方始终受下洗气流影响，结合图9（类比图2 给出的非直通甲板舰载直升机进场路径上的流场分布）可以看到：直升机进场过程中，随着距离机库后壁越近，纵向速度越来越小；在距离机库后壁小于6 m 的范围内变为反流；横向速度由正（左舷风）变为负（右舷风），且右舷风速随着距机库后壁距离缩短而增大；进场过程中始终受下洗气流影响，下洗速度先增大后减小。

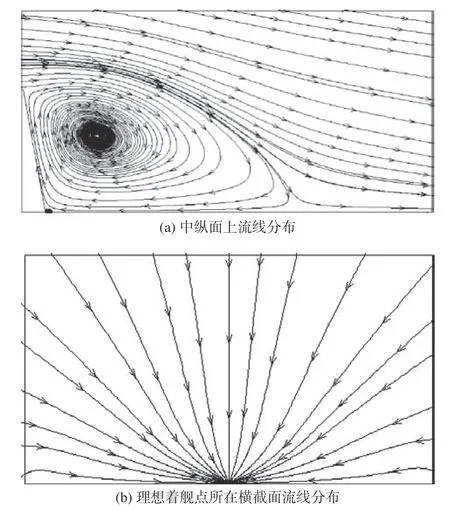
图8 0°风向角流线分布Fig.8 Streamline distribution when WOD=0°

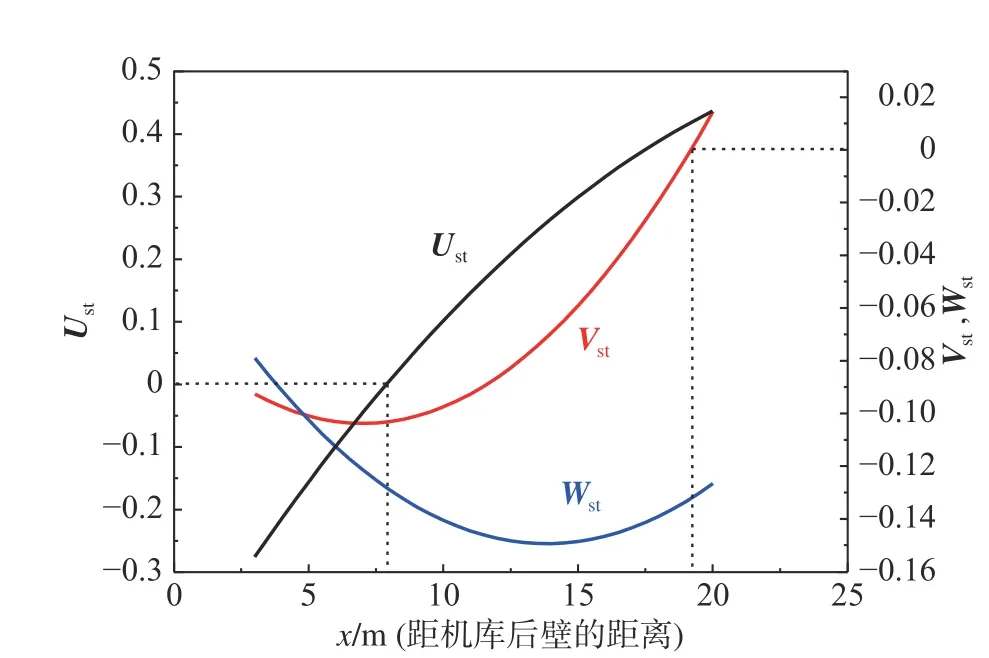
图9 0°风向角直升机进场路径上三向速度分布Fig.9 Velocity profiles induced by an approaching helicopter when WOD=0°

4.2 周期流场建模与验证

周期流场为Vp（三向速度分量为up、vp、wp），设计模型如式（8）所示：

式中：p、q、r为船体坐标系中的角速度分量（横摇、纵摇、艏摇），rad/s；t为时间，s。

特定纵横摇状态下的周期流场可简化为：

计算周期流场三向分量的主频和带宽的平均值，作为周期速度三向分量的固有频率和带宽，则时域场中的周期流场模型的构建转化为频域中求解频谱特征与空间的关系。周期流场的功率谱可以由单位白噪声通过成型滤波器生成：

式中：Sp(jω) 为周期流场速度频域值；j代表复数；ω为角频率，rad/s；Gp(jω)为周期流场滤波函数；Amax为周期流场信号峰值；Swn(jω)为单位白噪声。进而，周期流场可表达为：

式中，F-1[ ]为反傅里叶变换函数。

由于信号峰值、噪声能量及带宽与空间位置无关，因此，周期分量的建模进一步转化为周期分量信号峰值的建模问题：

三向速度周期分量信号峰值分布如图10 所示，属于三次超曲面。故周期分量信号峰值模型进一步简化为三维曲面拟合的问题，即：

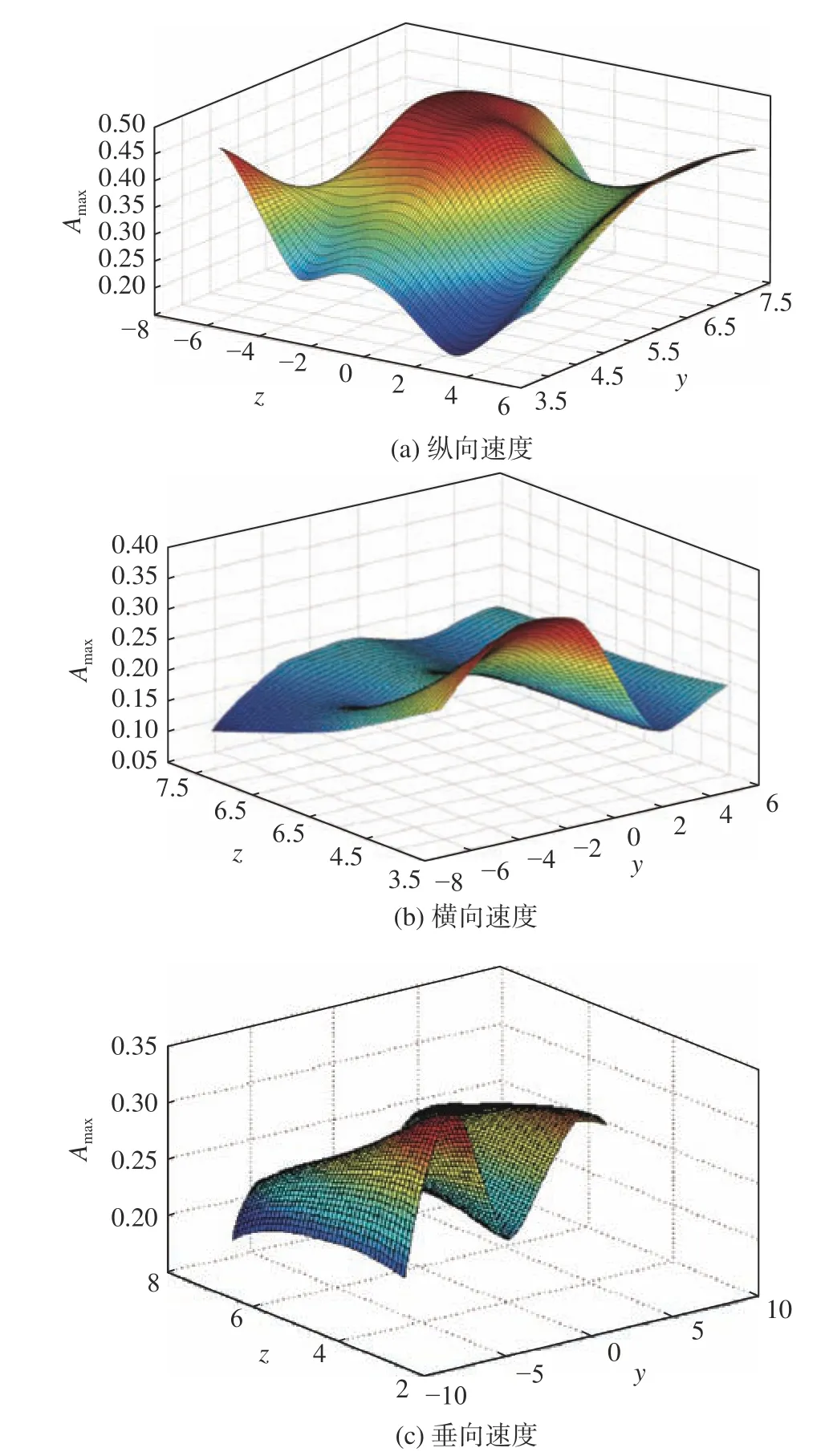
图10 三向速度周期分量信号峰值分布Fig.10 Spatial amplitude distribution of three periodic velocity components

基于空间位置的频谱信号峰值模型，运用最小二乘法优化模型参数，即可得到系数矩阵的结果。

根据周期分量的主频fmax和带宽B进行切比雪夫I 型低通滤波器设计，并对经信号幅值扩大后的白噪声信号进行滤波，得到周期频域特性如图11（a）所示，利用傅里叶变换进行频域-时域转换得到如图11（b）所示的时域仿真结果。

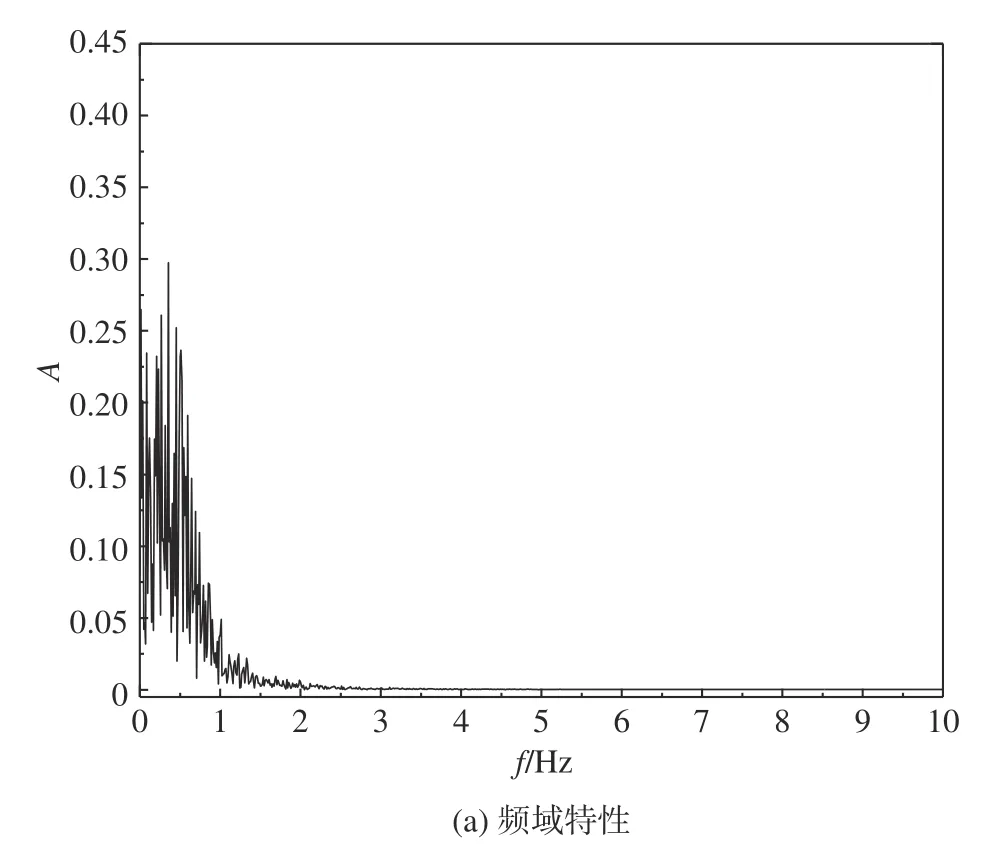
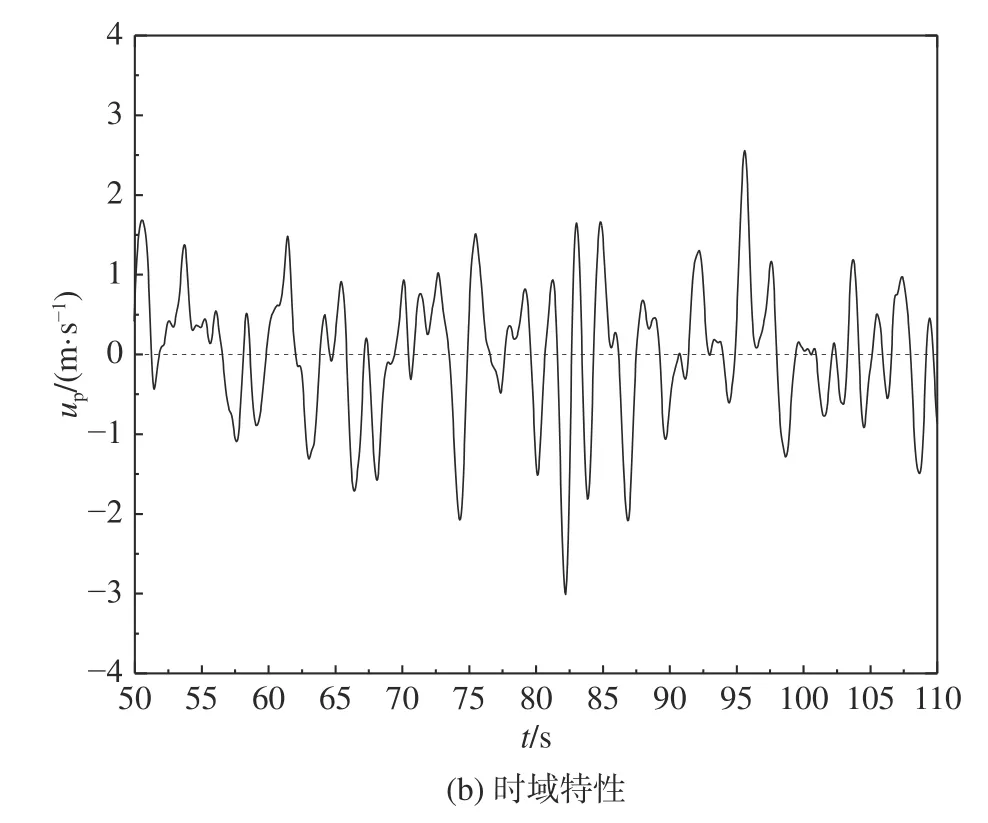
图11 周期流场模型仿真结果Fig.11 Simulation results of periodic airwake model

根据周期流场模型仿真得到的速度频域和时域特性与实测结果对比如图12 所示。对比发现，基于模型仿真得到的周期信号与实测结果存在一定的差距。这是因为实测信号中除周期分量外还包含随机分量，故两种方式得到的频谱变化规律相同但幅值上略有差异。

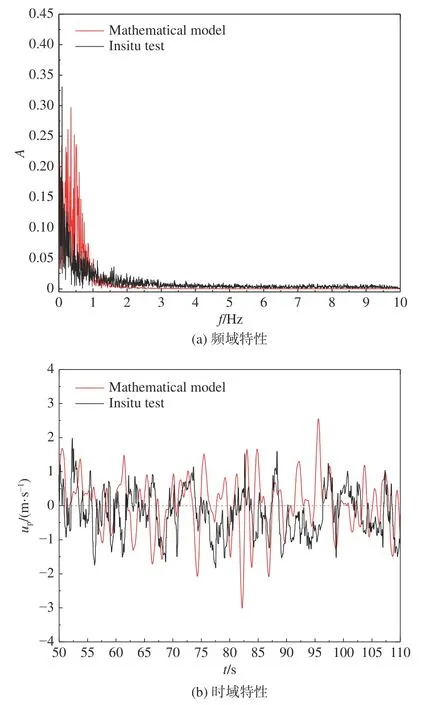
图12 周期分量模型仿真与实测结果对比Fig.12 Comparison between simulation and experiment of periodic component

4.3 随机流场建模与验证

随机分量为Vr（三向速度分量为ur、vr、wr），设计模型如式（14）所示：

与周期分量的建模过程相似，随机流场的功率谱可以单位白噪声通过成型滤波器生成：

式中：Sr(jω)为随机流场速度频域值；Gr(jω)为随机流场滤波函数；En为随机流场信号峰值（噪声能量幅值）。

进而，随机分量可表达为：

利用此滤波器对经噪声能量幅值扩大后的白噪声信号进行滤波，得到随机流场频域特性如图13（a）所示。利用傅里叶变换进行频域-时域转换得到如图13（b）所示的时域仿真结果。随机分量在频域和时域上的幅值均很小，且在频谱上均匀分布。

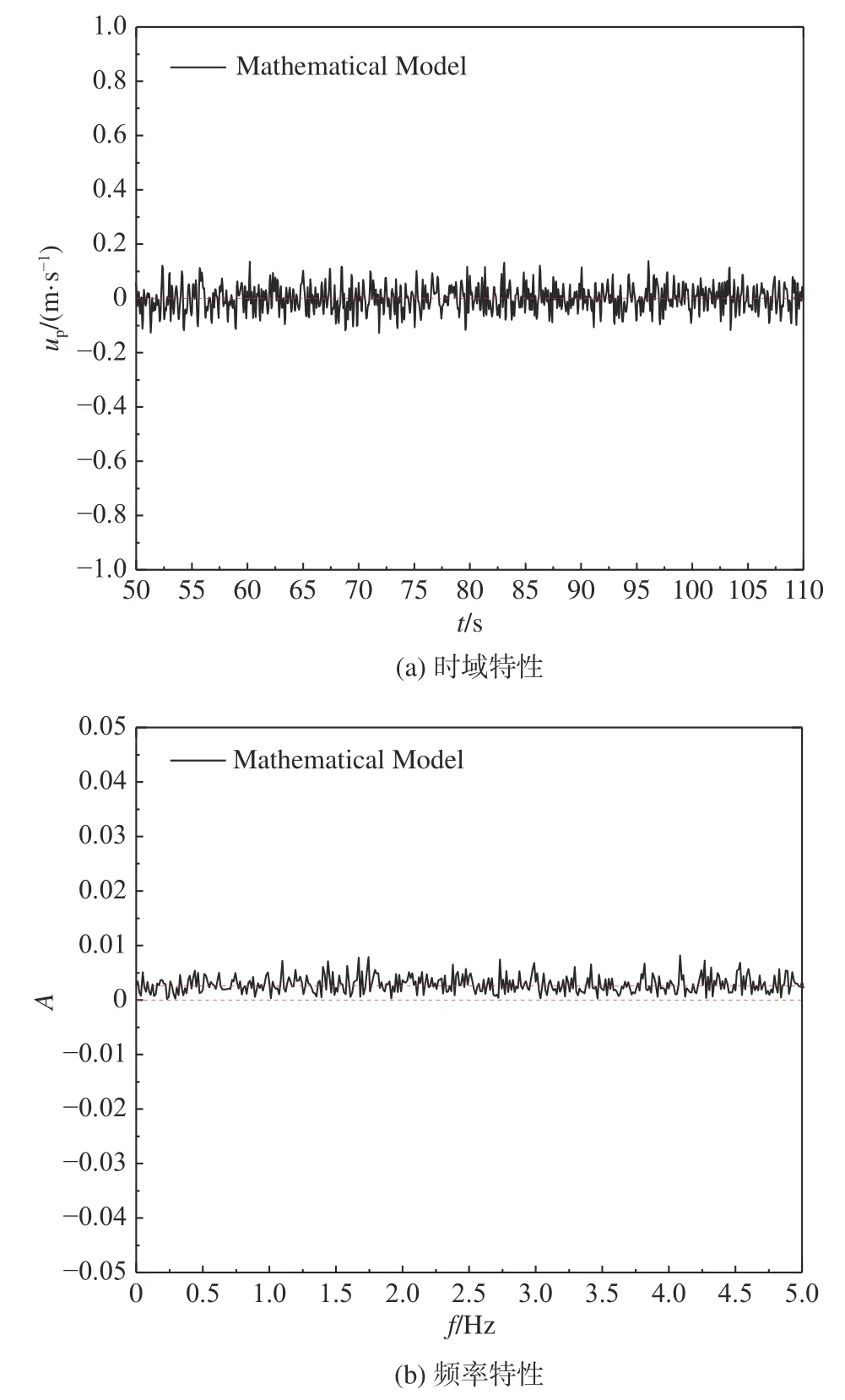
图13 模型仿真得到的随机分量的频谱和时域结果Fig.13 Time history and the corresponding frequency spectrum of the simulated random components

将随机模型和周期模型进行叠加后，与实测结果进行对比（图14），结果显示，论文中建立的瞬态流场模型与实测结果吻合良好。

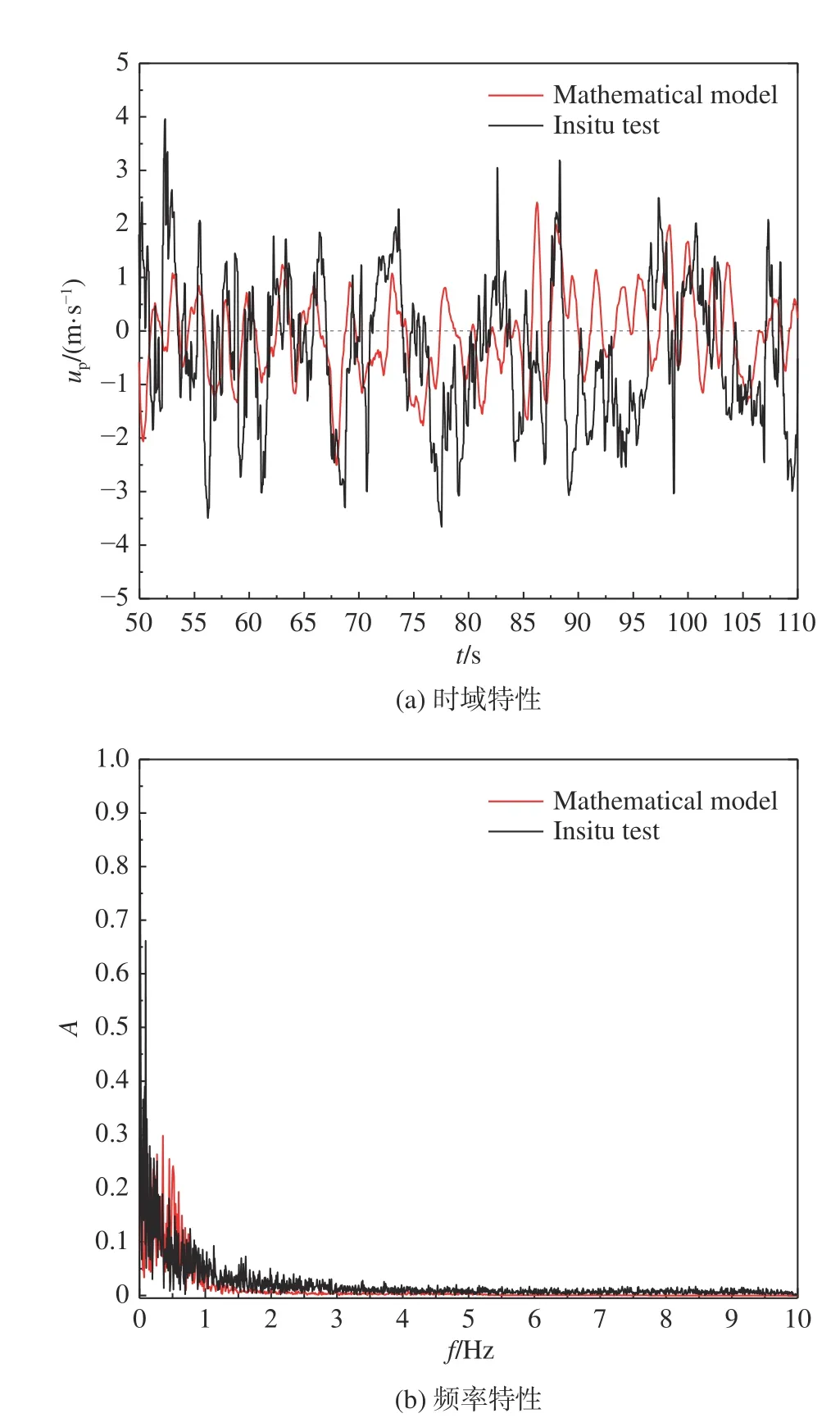
图14 周期和随机叠加模型仿真与实测结果对比Fig.14 Comparison between simulation and experiment for periodic and random components

5 结构化模型的综合分析与验证

通过第4.1～4.3 节的研究得到了非直通甲板舰船空气流场的稳态分量Vst、周期流场Vp和随机流场Vr，对Vairwake=Vst+Vp+Vr进行仿真，得到图15 所示的结果。与实测结果对比可发现，论文构建的流场模型可以较准确地模拟实测速度，两者时域和频谱吻合度均校好，证明了模型的有效性。

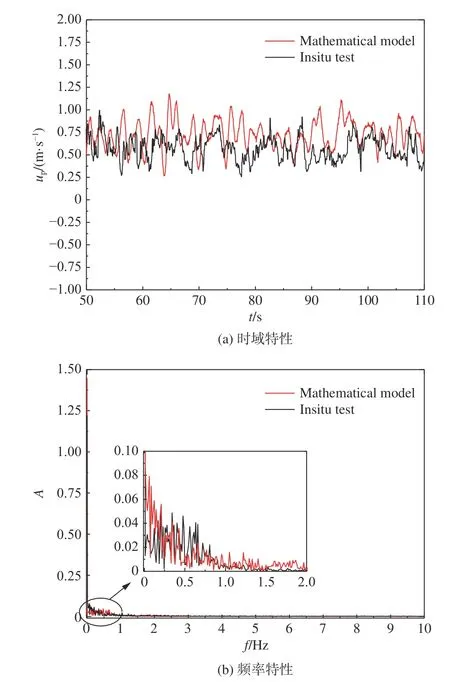
图15 模型仿真与实测结果对比Fig.15 Comparison between simulation and experiment

6 结 束 语

本文以非直通甲板舰船空气流场为研究对象，通过对流场特性进行频谱分析，解析了流场的形成机理，将其分解为稳态、周期量和随机分量，并成功构建了流场结构模型，仿真结果验证了模型的有效性。

稳态流场、周期流场和随机流场模型的成功构建，充分证明了稳态流场是非直通甲板舰船空气流场的主要组成部分，其是由甲板风与舰船结构决定的；周期流场是由舰船运动形成的，随船体的运动频率、大小及空间位置而变化；随机流场是由大气湍流及其他环境扰动引起的，可由白噪声经过滤波生成。

目前的空气流场模型是基于甲板0°风向角开展的建模，后续可针对0°～360°风向角范围内的模型进行进一步分析，探索包含甲板风风向角和舰船运动参数的建模研究。

通过叠加三种分量得到的空气流场避免了耗时耗力的实船测量试验，弥补了CFD 仿真和风洞试验数据无法涵盖真实环境影响的不足。本文非直通甲板舰船结构化空气流场模型的成功构建，为研究直升机在非直通甲板舰船的起降安全提供了新的途径，有助于大幅减少机-舰动态配合试验的工作量，有望使机-舰组合风限图的制定更加高效，同时也为开展机-舰动态配合实时仿真研究奠定了基础，对提高直升机的起降安全性和机-舰适配性能有指导意义。