面向目标参数估计的雷达低峰均比稳健波形设计
李 响 李德煦 王俊伟 郝天铎 曹兴龙
(1.沈阳科技学院 沈阳 110000;2.93363部队 沈阳 110000;3.国防科技大学 合肥 230000;4.93175部队 长春 130000)
0 引言
波形设计是雷达的关键技术之一。在实际情况中,由于环境的非平稳特性和先验知识估计方法的原因,使得杂波和目标的先验知识并不准确,造成所设计波形与实际目标和杂波不匹配从而降低波形估计性能。因此,为了有效防止波形的估计性能下降,需考虑进行稳健波形的设计。此外,为了增强发射机对发射功率的利用率,现有文献往往会考虑恒模约束。然而,恒模波形虽然是理想的发射波形,但其约束过于苛刻,往往为了便于实现,会转向低峰均比(Peak-to-Average Power Ratio, PAR)约束下的波形设计[1]。因此,PAR约束下的稳健发射波形设计已成为认知雷达亟待解决的重要问题之一。
文献[2]~[8]在先验知识不准确时,对稳健波形的设计进行了研究,其所运用的准则主要基于最小克拉美罗界(Cramer-Rao bound,CRLB)准则、最大互信息(mutual information, MI)准则和最小均方误差(Minimum Mean Square Error,MMSE)准则。文献[2]~[5]以最小CRLB为优化准则进行稳健波形设计。张向阳[1]和周子昂[3]在MIMO雷达系统中对相关问题进行了研究,在白噪声背景下,将信道误差限定在一个超球体构成的不确定集内,分别采用不同的方法实现了非凸优化问题到凸问题的转换,进而得到了MIMO雷达的稳健波形。H. Y. Wang[4-5]进一步假定信号与杂波无关,在杂波背景下采用半正定松弛(SemiDefiniteRelaxation,SDR)方法对MIMO雷达稳健波形协方差矩阵进行了设计。然而,这些文献只考虑了信号无关杂波。此外,文献[6]~[8]基于最大MI准则和MMSE准则对雷达稳健波形设计问题进行了研究。Y. Yang等人[6]较早地对此类问题展开研究,当目标的先验知识不准确时,假定目标功率谱密度位于一个上、下界均已知的不确定集内,基于极大极小化准则进行了稳健波形设计E. Grossi[7]将目标的散射系数和目标的分布协方差矩阵限制在一个不确定集内,根据Schur补充定理[9]将非凸优化问题转化为凸问题进行稳健波形的设计。但文献[6]~[7]均未考虑杂波的影响。而T. Naghibi[8]弥补了这方面的不足,在其信号模型中加入了信号相关杂波,在目标散射系数不确定集范围内进行了稳健波形设计。需要说明的是,以上文献均未对波形进行恒模或者PAR约束。当对波形加以恒模或者PAR约束后,会使稳健波形设计问题变得较为复杂,现有文献很少对此类问题进行研究。
针对该问题,以杂波冲激响应(Clutter Impulse Response, CIR)和目标冲激相应(Target Impulse Response,TIR)协方差矩阵特征值的不确定集表征CIR和TIR的波动范围,基于极大极小化准则构建MI准则下的问题模型,在不确定集范围内给出了MI最差情况下CIR和TIR的取值,并结合序列线性规划(Sequence Linear Programming, SLP)方法实现了PAR约束下的稳健波形设计。
1 信号模型
本文主要以扩展目标为研究对象,考虑信号相关杂波背景下的波形设计问题。文中,用CIR表征相关杂波特性[11],用TIR表征目标散射特性[10],则时域信号模型如图1所示。
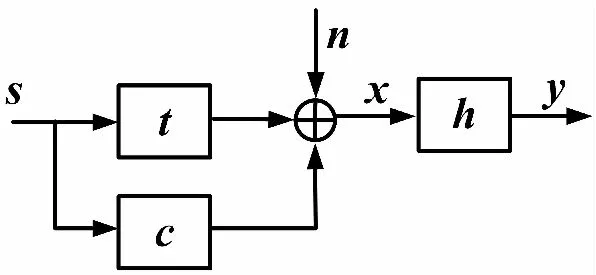
图1 相关杂波下的信号模型
图1中,长度为Ns的发射波形用s∈Ns×1表示;TIR和CIR分别用t∈Nt×1和c∈Nc×1表示[12];噪声和接收机权值分别用n∈Nn×1和h∈Nh×1表示;目标和环境的回波用x表示,其长度Nx=Nh=Ns+Nt-1。信号模型可表示为
x=t*s+c*s+n=Ts+Cs+n
=St+Sc+n=st+sc+n
(1)
y=hHx
(2)


(3)
同理,矩阵S亦可表示为

(4)
文中假定噪声向量n服从均值为0,协方差矩阵为单位阵的复高斯分布,也即n~CN(0Nn,Rn),其中,0Nn∈Nn×1的含义为Nn×1维零向量,Rn的含义为Nn×Nn维的非奇异Hermitian矩阵。如果噪声为高斯白噪声,则有其协方差矩阵取大于零的固定值,INn∈Nn×Nn代表Nn×Nn维单位阵);如果Rn不是单位阵,则代表Rn为高斯色噪声。CIR可以认为是服从高斯分布的,即c~CN(0Nc,Rc),Rc代表Nc×Nc维的非奇异Hermitian矩阵。同时,假定随机分布下TIR的目标向量t服从均值为0Nt,协方差矩阵为Rt的圆对称复高斯分布[13],即t~CN(0Nt,Rt)。
2 波形设计方法
2.1 基于互信息方法的问题描述
从信息论的观点出发,通过设计发射波形,使雷达回波中包含更多的目标信息,从而实现目标参数的有效估计[14]。因此,可采用目标与雷达回波之间互信息的大小作为对目标估计性能的度量,互信息越大,对目标参数的估计就越准确。本文以最大化MI为优化准则进行波形设计,目标t和回波x之间的互信息可表示为
I(x;t|S)=h(x|S)-h(x|t,S)
(5)
其中h(x|S)表示S已知时回波信号x的熵,而h(x|t,S)则表示S和t均已知时x的熵。其中,t和x服从联合高斯分布且可表示为[15]
(6)
令Rx=SRtSH+SRcSH+Rn,x的概率密度函数可表示为
(7)
则h(x|S)和h(x|t,S)可分别表示为

=ln det(SRtSH+SRcSH+Rn)+Nxlnπ+Nx
(8)
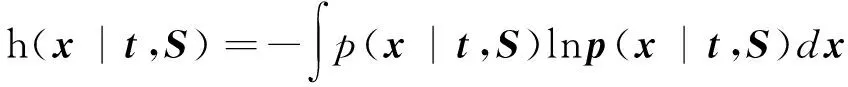
=ln det(SRcSH+Rn)+Nxlnπ+Nx
(9)
将式(8)和式(9)代入式(5),可得互信息为
I(x;t|S)=ln det[INx+SRtSH(SRcSH+Rn)-1]
(10)
可以看出,互信息是波形矩阵S的函数,可通过优化波形提高I(x;t|S),从而增强雷达的估计性能。接下来,对波形加以能量和PAR约束,并且在目标和杂波先验知识不准确的情况下进行稳健波形设计。
2.2 低峰均比稳健波形设计
考虑到需要对波形的幅度加以PAR约束,PAR一般定义为[16]
(11)
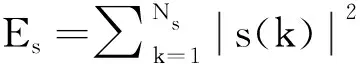
(12)
2.2.1 问题模型构建
结合式(10),同时考虑式(12)所示波形的PAR约束,则MI准则下的波形设计问题模型可表示为
(13)
其中,波形矩阵S的结构如式(4)所示。
可以看出,问题P的目标函数是非凸的,且两个不等式约束条件是非齐次的,同时优化问题中的矩阵变量S是波形向量s经过F函数映射的Toeplitz卷积矩阵,因此该优化问题较为复杂,很难直接得到波形的解析解。
首先,为了使问题P得以求解,需对其目标函数进行转化,应用矩阵求逆引理[18],可得
(14)
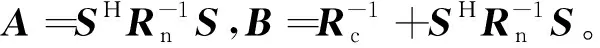
(15)
因此,PAR约束下基于极大极小化准则的稳健波形设计问题可表示为
(16)
2.2.2 不确定集下的稳健波形设计
对Rc和Rt进行特征值分解,则Rc和Rt可分别表示为[19]
Rc=UΣcUH
(17)
Rt=UΣtUH
(18)
其中Σc=diag(λc,1,…,λc,Nc),Σt=diag(λt,1,…,λt,Nt),其对角元素为Rc和Rt的特征值,同时也代表CIR和TIR功率谱密度的采样。由于Nt=Nc,则酉矩阵U可表示为
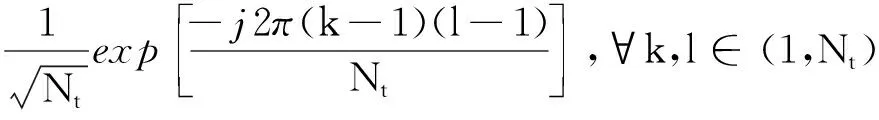
(19)
假定Rt和Rc的特征值在一定区间内波动,该波动区间与反馈信息的估计精度有关,于是不确定集可表示为
(20)

同理,高斯噪声也可表示为
Rn=VΣnVH
(21)
其中Σn=diag(λn,1,…,λn,Nn),V为Nn×Nn维的酉矩阵,其元素可通过式(19)表示(将Nt用Nn代换)。
将式(17)、式(18)和式(21)代入式(16)所示问题中的目标函数,可得
(22)
式(22)所示极大极小化问题的目标函数是非凸的,且第二个约束条件属于非齐次不等式约束,因此该问题是一个非凸问题[20]。
由于式(22)所示优化问题中波形与噪声、CIR和TIR的协方差矩阵是互相独立的,因此目标函数中的极大化和极小化的位置可互换,因此其目标函数也可转换为
(23)
此外,当λt,i和λc,i已知时,根据Hadamard不等式[21],若要使目标函数取得极大值,波形矩阵S应满足如式(24)结构。
(24)
其中Λs=diag(λs,1,…,λs,Nt)。将式(24)代入式(22)所示问题的目标函数,则优化问题可转化为
(25)
可以看出,式(25)所示问题的目标函数与λc,i成反比,而与λt,i成正比,于是内部极小化问题所示目标函数可表示为
(26)
因此,优化问题可转换为
(27)
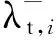
3 仿真实验与分析

(28)
(29)
其中ui表示服从标准正态分布的随机变量,于是不确定集变化范围可表示为图2所示。
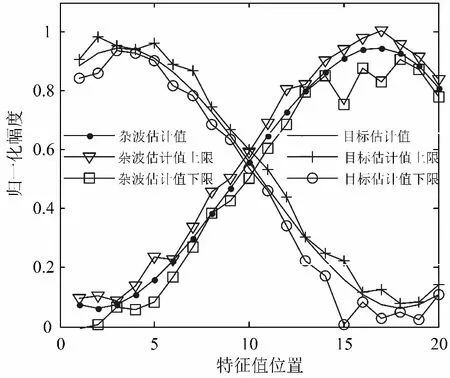
图2 目标和杂波特性不确定集区间
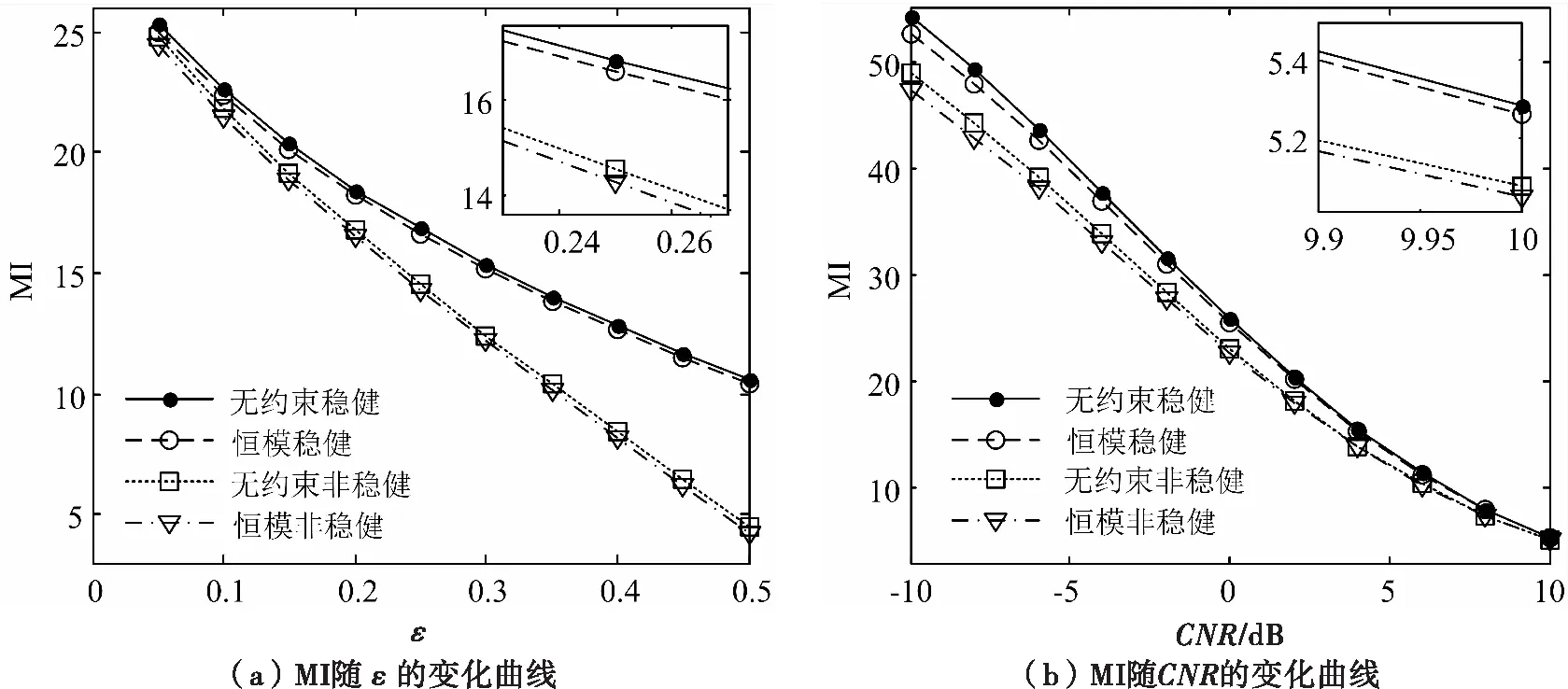
图3 不同估计波形稳健性能对比

图4 优化波形的MI随PAR约束的变化
图5展示的是不同PAR值下波形的实部和虚部,μ=Ns表示在只有能量约束时所求的波形,可以看出点此时分布半径较大,也间接说明波形峰值幅度较大,发射端功率利用率低,实用性较差。而当μ=1时,此时所形成的是一个原圆,说明波形的幅度是恒定的;而当μ=2时,圆的分布半径略大于μ=1时波形,且波形的MI高于恒模波形。从图4和图5可以看出,低PAR波形(例如μ=2)不仅能较好地兼顾发射机的效能(μ=2时分布半径较小,说明峰值幅度较小),亦可以使雷达具有较好的估计性能(比恒模波形有更高的MI),说明低PAR波形实用性较强。
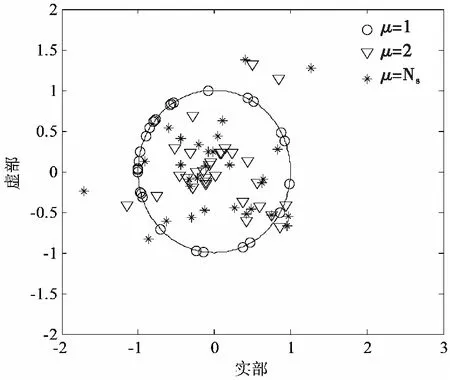
图5 不同PAR约束下波形的实部和虚部
此外,对算法的有效性进行验证。将优化波形与相位编码波形和线性调频(Linear Frequency Modulation, LFM)波形进行对比,如图6所示,其中LFM波形可表示为[10]
(30)
图6为不同发射能量下优化波形与常用波形的对比,从图6可以看出,随着发射能量增加,三种波形的MI取值逐渐增大,产生的优化波形对应的MI要优于相位编码波形和线性调频波形,验证了所提方法有效性。
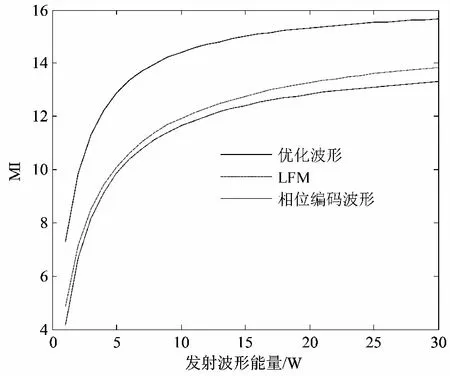
图6 不同波形估计性能对比
4 结束语
为了提高雷达功率放大器的效能,增强波形在TIR和杂波先验知识不准确时的稳健性能,基于极大极小化准则,研究了任意PAR约束下的认知雷达稳健波形设计问题。以CIR和TIR协方差矩阵特征值的不确定集表征CIR和TIR的波动范围,基于极大极小化准则构建MI准则下的问题模型,在不确定集范围内给出了MI最差情况下CIR和TIR的取值,并结合SLP方法实现了PAR约束下的稳健波形设计。仿真结果表明,与常用波形相比,优化波形具有更好估计性能,在目标和信号相关杂波不确定集范围内,所求波形具有较好的稳健性能。

