基于压缩感知的频率捷变雷达切片干扰抑制技术研究
刘 尚 蒋金华 李麒麟
(江南机电设计研究所 贵阳 550009)
0 引言
随着高速采样、超大规模数字处理、射频直接存储等技术的进步,电子干扰技术也快速发展。干扰机产生的干扰波形能够实现与雷达探测波形相参,形成对雷达回波信号在多个域上的全面覆盖。不仅抵消了雷达匹配滤波带来的抗干扰增益,而且大幅压缩了雷达的探测距离。因此,日益复杂的强对抗电磁环境对雷达的抗干扰技术能力提出了更高的作战要求。
近年来,信号处理领域里“压缩感知”理论的稀疏恢复技术取得了新的突破,改变了经典雷达信号处理基于“匹配滤波”的传统思想,将“稀疏恢复”思想与频率捷变信息处理技术相结合[1-2],通过发射时-频维快速、随机捷变的雷达波形,并以干扰条件下目标信息最优重建为目的进行回波信号处理,在接收处理过程中去除杂波和干扰后,通过基于非完整观测的目标信息“最优重建”,解决目标在复杂电磁干扰环境下的探测问题,改变雷达在电子对抗中的被动局面。为此,本文从压缩感知稀疏恢复算法的角度,开展了时-频维上频率捷变处理技术相关方面的研究。
1 压缩感知稀疏恢复理论
一直以来,奈奎斯特采样定理是指导如何进行信号采样的重要理论基础。该定理指出,采样速率应大于等于信号带宽,原始信号才能由采样信号不失真地精确重构。近年来压缩感知理论的研究则突破了此采样定理对信号采集与处理的限制。
由Doho、Cades[3-4]及华裔科学家Tao等人提出的压缩感知理论表示:如果信号通过某种变换(如傅立叶变换,小波变换等)后,是可稀疏表示或可压缩的,则可以设计一个与变换基不相关的测量矩阵测量信号,对得到的测量值求解优化,实现信号的精确或近似重构[5]。压缩感知是针对稀疏信号或可压缩信号提出的基于数据采集和数据压缩为一体的新型信号处理方法,推动了信息领域向前发展。它与传统的信号采样、编解码的方式有着很大的不同,传统的信号采样、编码、解码的过程如图1所示。
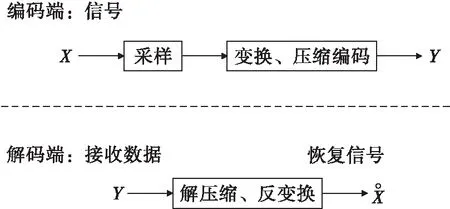
图1 传统的信号采样、编解码理论框图
压缩感知理论对信号的采样、压缩编码发生在同一个步骤,利用信号的稀疏性,以远低于奈奎斯特采样率的速率对信号进行非自适应的测量编码,如图2所示。测量值并非信号本身,而是从高维到低维的投影值,从数学角度看,每个测量值是传统理论下的每个样本信号的组合函数,即一个测量值已经包括了所有样本信号的少量信息。解码过程不是编码的简单逆过程,而是利用信号稀疏分解中已有的重建方法在概率意义上实现信号的精确重建或者一定误差下的近似精确重建。解码所需测量值的数目远小于传统理论下的测量数。

图2 基于压缩感知理论的信号采样、编解码理论框图
压缩感知理论主要包括三部分:一是信号的稀疏表示;二是设计测量矩阵对信号进行观测采样[6],要在降低维数的同时保证原始信号x的信息损失最小;三是稀疏恢复算法,利用M个观测值无失真地恢复出信号长度为N的原始信号。
其中,第三部分信号的稀疏恢复是从M维的测量信号y恢复N维原始信号x,如式(1)所示。
y=Φx=ΦΨs=Θs
(1)
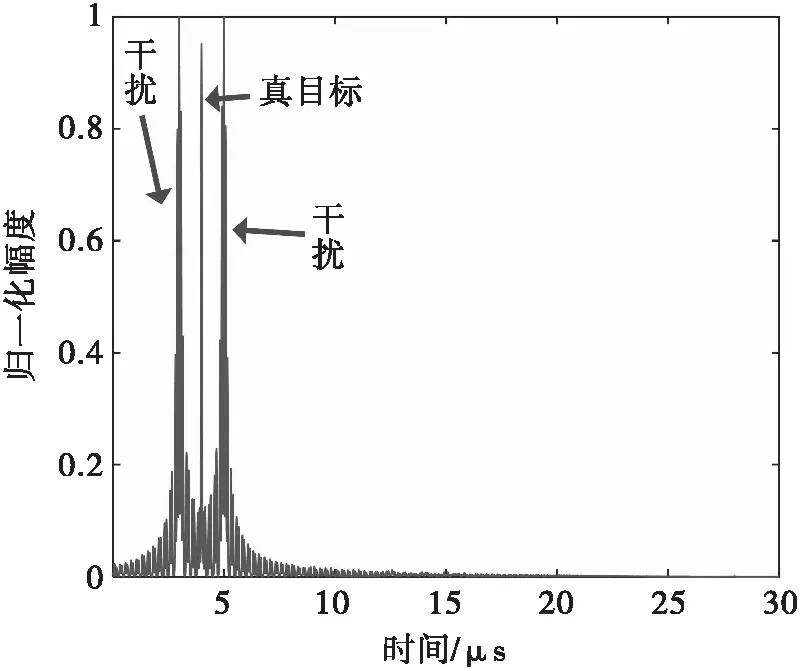
其中,s是信号x在Ψ域的变换向量,Θ又称为感知矩阵。由于s是K稀疏的,且K (2) 目前常用的用于求解式(2)中的优化问题的算法可以简略归纳为3类:最小l1范数法、贪婪算法、迭代阈值法。其中贪婪算法主要思想是通过迭代计算x的支撑集获得重构信号,具有低复杂度和简单几何运算的优点。文献[7]中描述了常用的贪婪算法,包括匹配追踪MP(Matching Pursuit, MP)算法,正交匹配追踪OMP(Orthogonal Matching Pursuit, OMP)算法,压缩采样匹配追踪COSAMP(Compressive Sampling Matching Pursuit, COSAMP)算法,子空间追踪SP(Subspace Pursuit)算法以及它们的改进方法。 “捷变”一直是雷达反侦察抗干扰的有效手段。在快速发展的干扰威胁刺激下,捷变的应用在新的信号处理理论推动下,正朝着多维、综合、全相参处理的方向进一步发展。频率捷变技术的出现改变了雷达发射单一不变波形的局面。频率捷变[8]是指雷达发射相邻脉冲或脉冲组的载频在一定范围内快速变化,在整个相参捷变带宽内实现多个频率的同时发射,作战过程中极大改善了雷达的反侦察和抗干扰性能,成为现代雷达普遍使用的抗干扰技术手段。 信号稀疏恢复技术由于利用了观测对象的稀疏特征,可以用远低于经典奈奎斯特频率的采样率获取观测对象的完整信息。在雷达信号处理方面,稀疏恢复技术首先被应用到探地、穿墙和高分遥感成像等领域,有效降低了获取目标高分辨信息所需的带宽和采样速率。此外,在多维信号处理方面,稀疏恢复技术有效降低了杂波谱估计所需的样本个数,提高了非均匀杂波中的目标检测性能。还有学者将稀疏恢复技术应用于随机步进频脉冲的高分辨成像处理中,证明了稀疏恢复技术在频率捷变波形的信号处理中的适用性和应用潜力。 本文将稀疏恢复与频率捷变处理技术相结合,通过雷达发射波形在时-频维的快速随机捷变,使干扰机难以获取对波形的多维完整观测,难以在所有波形维度内形成对目标回波完整、精准破坏。在此基础上,雷达利用自身发射波形已知的信息优势,通过稀疏恢复技术利用对目标的非完整观测重建目标信息,完成目标检测跟踪和抗干扰的作战任务。 传统理论认为,当发射波形捷变(尤其是频率捷变)时,目标散射特性会存在起伏,即所谓捷变“去相关”现象。分析表明,对于理想点目标基本不存在捷变引起的目标起伏。而当目标是复杂目标时,频率捷变引起的目标起伏是由于在一个分辨单元内存在多个散射中心,各中心回波的矢量叠加效果会随电磁波波长的变化而变化。因此,基于稀疏恢复的捷变雷达信号处理应结合该波形的高分辨特性,采用点散射类模型,将目标回波建模成各个散射中心回波的矢量叠加。 捷变频雷达发射波形为时-频维快速、随机捷变的复杂波形,雷达以脉组为单元进行信号发射,每一个脉组包含N个脉冲,称为一个处理周期。在一个处理周期内,不同脉冲具有不同的发射载频,捷变频雷达发射的探测波形示意如图3所示。 图3 捷变频雷达发射探测波形示意图 因此,目标多散射点回波建模仿真可以通过稀疏方程公式(3)表示。 Y(t)=Φx(t) (3) (4) 稀疏恢复的测量矩阵包含了散射点的距离和速度信息、信号频率调制信息等,以此构造的稀疏测量矩阵可将高维信号投影到低维空间上,尽可能多地将散射点重要的信息特征保留并完成大概率的恢复。公式(4)中,对不同脉冲的发射载频信息进行了公式推导,对相关散射点的距离和速度分辨单元变量进行了分解,其中f0为信号发射基带载频频率;Mn为一个相参处理周期中脉冲个数;Δf为一个相参处理周期中捷变频率变化量;Rk为雷达与对应散射点之间的距离;n为脉冲回波信号的序号数;Tr为脉冲重复时间(PRT);vl为目标散射点相对雷达的速度离散化单元的速度值。 公式(3)中Y的行向量对应的是由相参处理周期内的N个脉冲的回波信号组成N×1维向量,X中的元素为观测场景中目标散射点的N×M个速度-距离分辨单元中散射点强度。Φ中的每一列即为对应单位强度散射点的回波向量。对于捷变频雷达,发射的波形为时-频维快速、随机捷变的复杂波形,对应X中的元素产生的分辨单元信号的维数N远远大于采样数据维数M,利用X的稀疏性,测量矩阵Φ的稀疏系数中只有K个非零稀疏,且满足M≥K,因此可以通过求解稀疏方程公式(1)的逆问题得到信号X。 切片干扰的原理是利用脉冲压缩雷达信号处理中匹配滤波带来的相干增益来提高切片干扰的压制或者欺骗效果,其实现途径是基于数字射频存储器、直接数字合成器对雷达信号进行不失真采样、存储、信号处理和形成模拟信号后转发,这样转发的干扰信号同雷达信号高度相参,干扰信号通过匹配滤波后可以形成单个假目标或多个假目标群。 假设雷达信号为线性调频信号S(t),脉宽为T,带宽为B,调制斜率K为B/T,则有如式(5)所示。 (5) 假设真目标距离为RM,则雷达至目标的单程延时为τM=RM/c,其中c为光速。由此可得雷达的目标回波信号RM(t)为 (6) 其中AM表示目标回波幅度值,目标回波RM(t)通过匹配滤波器h(t)的响应OM(t)为 (7) 式(7)中,⊗为卷积运算,h(t)=S*(-t),O(t-2τM)表示距离为RM=c·τM的目标回波通过匹配滤波器h(t)的响应。 为了简化模型,切片干扰的数学模型不考虑多普勒频移,只在时域维增加转发延时处理,可简化为将一个矩形包络脉冲串(也称为间歇采样信号)同雷达信号相乘,然后根据不同的组合方式将其转发。间歇采样信号的数学模型可表示为 (8) 重复转发切片式干扰的工作示意图如图4所示。 图4 重复转发切片干扰工作示意图 因此,切片干扰信号可表示为 (9) 而雷达接收到的切片干扰的回波就可表示为 RJ(t)=AJ·J(t-2τM) (10) 假设雷达脉冲宽度为20μs,带宽为40MHz,系统采样频率为100MHz。切片干扰的采样周期为6μs,占空比为1/3,转发延时为2μs,重复转发次数为2次,干扰调制频移为6MHz,信干比为-10dB。则对目标信号加切片干扰回波脉冲压缩后的仿真结果如图5所示。 图5 目标信号加切片干扰脉压后干扰效果 经过干扰调制频移后的重复式切片干扰经脉冲压缩后造成的假目标在时域上3μs和5μs处各形成了一个假目标群,这两个假目标群是干扰重复转发两次所致。由此可知,切片转发干扰经过雷达脉冲压缩后可以获得众多幅度不一的假目标,这些假目标相对于真目标幅度有强有弱,再通过调频的方式,可以实现假目标超前或滞后的欺骗干扰,对雷达实战化能力非常不利。 第二章中介绍了几种常用的重建算法,贪婪追踪算法是压缩感知理论中最常用的稀疏信号重建算法,其主要思想是通过迭代计算X的支撑,即通过每次迭代时进行局部最优化寻找各个非零系数来获取信号矢量的逼近。该类算法主要是采用某种准则在每次迭代过程中从冗余字典选取一个或几个与观测值余量最大相关的原子,最终寻找一组与观测值匹配的最稀疏的原子组合,从而实现信号的重建。其算法的优点是对于维数较低的小尺度信号问题运算速度很快,计算复杂度相对较低。 为了完成对时-频维捷变多散射点回波稀疏重构研究中稀疏方程的求解,即求解以下的优化问题: min‖X‖1, s.t.‖Y-ΦX‖2≤ε (11) 式(11)中,L1模范数‖X‖1定义为 ‖X‖1=|X1|+…|Xn| (12) 得到的解Xopt满足如式(13)误差关系为 (13) (14) 基于以上稀疏方程求解的思路,本文选择相对收敛速度较快且重建算法中使用最多的正交匹配追踪OMP算法进行重建技术研究。首先从测量矩阵Φ的每一列中,选出与原始信号最接近的某一列向量,稀疏化后求出残差,接着选出残差最接近的那一列向量并进行正交化处理,将第n次的迭代残差与测量矩阵Φ做内积取绝对值最大的元素,计算了近似解后再更新余量,由于每一次迭代中,选择Φ中与y的剩余部分最相关的列,然后从y中抽取该列对y的贡献,再对其进行冗余迭代,对应时-频维捷变相参多散射点回波建模的稀疏重构方程在经过有限次的迭代后,算法能够收敛到信号的稀疏解,信号的稀疏恢复质量较高,且收敛速度快。正交匹配追踪OMP稀疏恢复算法相对具有普适性,本文通过理论分析和稀疏恢复算法在时-频维捷变多散射点回波稀疏重构技术上的仿真应用验证了恢复重建的可行性。 假设模拟距离分别为d1=475m,d2=500m,d3=525m的相邻近三个目标,使用线性调频脉冲压缩信号对目标进行测距,脉冲压缩前信噪比为SNR=5dB。引入时间域复制切片转发式干扰,6个切片转发,在干信比=40dB条件下,比较剔除补零的脉冲压缩与稀疏重构脉冲压缩结果。 从图6(a)和图6(b)中可以看出,无干扰条件下目标脉冲压缩的结果有相当明显的三个尖峰,而引入切片干扰后的时域图中除了目标信号外,还存在相应的复制切片干扰;从图6(c)中可以看出,剔除补零脉冲压缩结果的弱目标已经被强目标副瓣淹没;而从图6(d)中可以看出,采用稀疏恢复方法实现的脉冲压缩结果与原始信号对比,具有较高的恢复精度。 图6 剔除补零与稀疏恢复方法脉冲压缩结果对比 本文针对重复转发切片式干扰,提出了将稀疏恢复与频率捷变处理技术相结合的抑制方法,并给出了相应的计算机仿真结果。该方法通过波形在时-频维的快速随机捷变,利用对目标的非完整观测重建目标信息,实现高效的目标回波相参积累,有较好的目标分辨能力,可在较高的干信比下完成切片干扰的抑制,实现目标在复杂电磁干扰环境下的检测与跟踪。本文旨在验证基于稀疏恢复的频率捷变信息处理方法的可行性及有效性,可稀疏恢复捷变雷达波形优化设计、时/空/频/码等多个维度的联合捷变处理、稀疏恢复贪婪追踪算法的优化问题仍需在今后的工作中进行深入研究。2 基于稀疏恢复的频率捷变处理技术
2.1 时-频域频率捷变目标回波模型
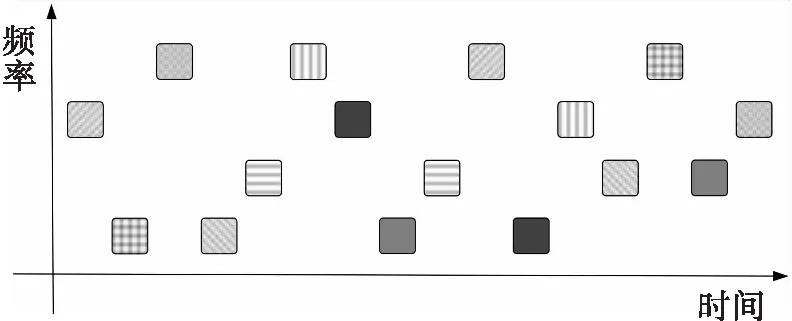

2.2 切片转发干扰信号模型

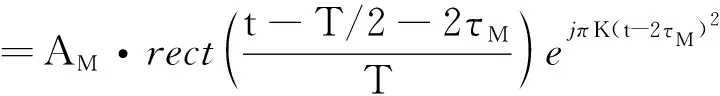



2.3 稀疏恢复重建算法
3 稀疏恢复处理的切片干扰抑制仿真

4 结束语

