上海期货交易所原油期权的价格偏离研究

摘 要：2021年6月21日，原油期权在上海期货交易所上市交易，我国原油期权市场正处于发展的关键时期，为了满足期权市场发展及对冲有效性的需要，期权的合理定价是其中的重要一环。本文在结合了几何布朗运动、蒙特卡洛模拟与GARCH族模型对上海期货交易所原油看涨期权进行估值并与市场价格的对比中发现，俄乌战争背景下，随着原油期权价格的大幅波动，原油期权的市场价格与价值发生了较大幅度的偏离，这种偏离会在波峰达到最大，而且深度实值的期权的市场价格仅反映了内在价值并没有反映时间价值。本文通过对影响期权价值的底层因子进行分离并运用计量手段做进一步分析，发现导致这种偏差的主要原因是上海期货交易所原油期权市场价格几乎不对波动率和剩余到期期限进行定价，而且对标的资产价格因素反应不充分，这种不充分会随着虚值的增加而增加，并不是由战争所引起的。

关键词：俄乌冲突；原油期权；期权定价；蒙特卡洛模拟；GARCH

本文索引：沈卓成.<变量 2>[J].中国商论，2023（06）：-128.

中图分类号：F830.9 文献标识码：A 文章编号：2096-0298（2023）03（b）--06

我国原油期权市场正处于起步阶段，具有极大的发展潜力与空间，因为衍生品更大的作用还是转移风险实现对冲、实现风险管理而非投机，原油期权市场的发展是必然趋势。

一方面，市场将趋于成熟且更加有效。在有效市场中，价格将会反映所有信息，商品的价格总是会趋近于该商品的价值。合理的价格就是市场发展的必然要求，认清其来源则可以采取更好的方法来引导价格走向合理。

另一方面，衍生品作为风险转移、对冲工具需要合理的价格及价格变动。例如，某公司需要用期权完全对冲其所面临的原材料价格变动风险，从理论上讲，应通过Delta与Gamma进行对冲计算期权头寸。當期权价格无效时，Delta与Gamma便失去意义，期权价格不会因为标的资产价格的变动而产生相应合理的变动，即使进行了对冲，公司整体也会暴露在很多不可预期的风险下。当对冲失去意义，对冲者数量减少，整个衍生品市场会充斥着更多的投机气氛。因此，合理的价格及价格变动是衍生品作为对冲工具的必要条件。

因此，借着俄乌冲突中各效应被放大的机会，如原油期权标的资产价格的大幅变动及波动率的急剧上升使得这些因素与原油期权价格的联动关系更加明显，本研究能更精确地找出我国期权市场价格偏离价值的原因，并为后续期权定价的合理化铺平道路。

1 上海期货交易所原油期权的估值

本文分别选取上海期货交易所4月及5月到期的六份看涨期权合约（代码分别为sc2204C500、sc2204C600、sc2204C700、sc2205C500、sc2205C600、sc2205C700）为研究对象，因此下文研究中若未专门指出是某期权合约则所指期权均指该六份期权合约或其中之一。根据合约代码，其标的资产分别为上海期货交易所上市的同月到期的原油期货（代码为sc2204、sc2205）。基于战争开始时的现货价格，行权价为500元、600元、700元的看涨期权分别对应深度实值、接近平值与深度虚值，而且上海期货交易所仅有4月及5月到期的原油期权交易日期能够覆盖战争前夕与爆发后，这样的选取能够更好、更直观地对结果进行展示与对比。本文将所有合约的每日结算价作为每日价格，所有价格数据均来自Wind数据库。

此外，本文选取中国20年国债到期收益率作为无风险收益，其值为3.4%，数据来源于Trading Economics。

1.1 波动率参数的估计

1.1.1 数据波动率集聚效应的存在

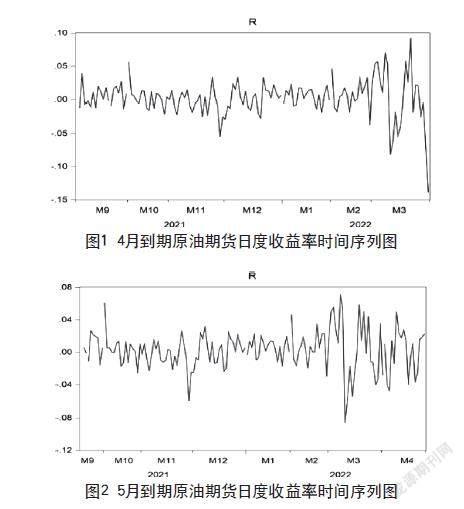
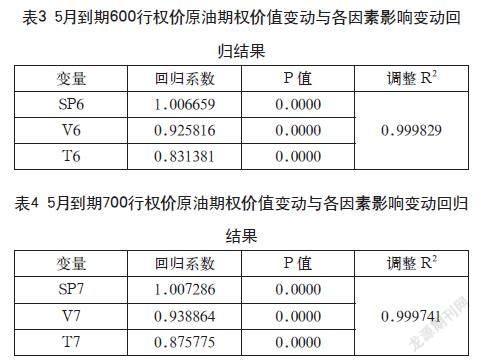
根据Black-Scholes模型可知，期权的价值会受到波动率影响，战争爆发后，原油期货的价格波动明显增大。通过每日结算价数据，得到原油期货合约每日的对数收益率数据（见图1、图2）。

由此可以看出，原油期货的收益率时间序列出现了较明显的自相关现象，即反映为原油期货收益率数据的波动率平均水平发生了较大的变化，因此仅将历史波动率作为期权估值中的波动率数据并不合理。

1.1.2 GARCH族模型的建立

本文将引入GARCH族模型对标的资产收益率进行建模，得到标的资产每日更新的日度收益率，以解决波动率集聚问题。

1982年Engle提出自回归条件异方差（ARCH），将拟合方程的误差视为其滞后项的函数，使滞后数据的波动性对预测数据产生影响，从而解决波动率集聚的问题[1]。后在1986 年Bollerslev提出了广义自回归条件异方差（GARCH），对Engle所提出的ARCH模型进行了改进，减少了模型待估参数以更好地估计资产波动率[2]。随后，1986年Engle与Bollerslev共同提出了IGARCH模型，去掉常数项但要求模型中所有参数之和严格等于1。1991年Nelson提出EGARCH模型，用自然对数刻画非对称性[3]。1994年Zakoian提出TGARCH模型，以虚拟变量体现杠杆效应[4]。

根据所收集数据，本研究发现，sc2204原油期货合约在2021年9月1日前交易不活跃，sc2205原油期货合约在2021年9月15日前交易不活跃，为了建模的准确性，本研究剔除了交易不活跃的时间段，对两组数据分别从2021年9月1日和2021年9月15日开始建模。

借助Eviews，本研究对两种原油期货收益率数据分别建立了GARCH族模型。本文主要通过AIC、SC指标在不同GARCH族模型间进行对比以挑选出最优模型。经过各GARCH模型的对比，本文选用了IGARCH模型，其建模结果如下：

sc2204：

sc2205：

其中，Rt和Rt-1分别代表不同时间点的资产收益率，分别代表不同时间点的均值方程残差值，分别为不同时间点的资产波动率。

根据建立的IGARCH模型，可以计算出标的资产日度波动率数据。

1.2 美式期权的估值

1991年Longstaff与Schwartz提出了以蒙特卡洛模拟的方法对美式期权进行定价[5]，后于1994年Stentoft通过研究证明了该方法的优越性[6]。

当每个周期的增量相互独立并服从正态分布时，随机过程被定义为布朗运动，如果随机变量的对数遵循布朗运动，那么它遵循几何布朗运动，这是最简单的连续随机过程，也是描述证券价格随机性的基本模型[7-8]。研究表明，几何布朗运动可以很好地预测股票价格，尤其是在短期内[9]。此外，Postali和Picchetti所做的研究得出的结论是，只要均值回归的速度较慢，几何布朗运动就可以更好地代表油价的运动[10]。基于Black-Scholes模型的思想，本文将借助几何布朗运动，采用蒙特卡洛模拟对期权进行估值，其公式为：

其中，T和t是年份的时间点，ST和St是相应时间点的资产价格，α是预期收益，σ是标准差，z是正态分布累积概率分布函数的反函数的随机值。

因此，通过生成-1～1间的随机数，代入正态分布累积概率分布函数的反函数，通过上述公式就可以得到一条模拟价格路径，通过寻找该路径上的期权收益现值的最大值，即可得到期权的价值。

最后，本研究通过重复进行100万次模拟并求出输出结果的均值来获得期权的估值，其中标准误数值已很小，可忽略不计。

2 上海期货交易所原油期权的市场价格与价值对比

根据前文的期权估值模型，本文将2022年2月16日至2022年3月15日交易日的市场价格与价值进行了对比（见图3至图8），其中2022年2月24日为战争开始后的第一个交易日。

观察图3和图6，不难发现深度实值期权的市场价格在这段区域内一直被低估，两者一直存在着较大的偏离。

由图3至图8中多图可以发现，随着战争的爆发，在期权市场价格与价值均急剧上升时，期权价值上涨的幅度明显大于期权市场价格的上涨幅度，而当期权的市场价格与价值均急剧下降时，期权的价值变化幅度同样也极易大于期权市场价格的变化幅度。

为了更直观观察，本研究对sc2205C700原油期权3月3日至4月13日（上海期货交易所五月期权合约最后交易日）的价值进行了估计，并与实际市场价格进行了对比（见图9）。

可清晰地观察到，在期权价值与市场价格的大幅上升时，期权价值的上涨量明显大于市场价格的上涨量；而在期权价值与市场价格大幅下跌时，其价值下跌量也明显大于市场价格的下跌量。

综上，本研究发现，深度实值的上海期货交易所原油看涨期权及俄乌战争爆发后的非深度实值看涨期权的市场价格与价值间均有较大的偏差。前者市场价格一直处于被低估状态，而两者市场价格在上涨趋势中极易被低估或扩大被低估程度，在下跌趋势中该程度又极易有所降低，最终在波峰附近产生最大偏离。

3 俄乌背景下上期易原油期权市场价格与价值偏离的原因剖析

本文主要将期权的每日价值变动进行分解来进一步研究上海期货交易所原油期权市场价格与价值偏离的原因，即在无风险利率和行权价不变的条件下，期权价值只受标的资产价格、波动率和剩余到期期限三个因素的影响，在原先对美式期权估值的方法基础上，本研究分别只应用第t+1天对应标的资产价格、波动率和剩余到期期限中的其中一个因素，将其他两个因素保持在第t天所对应的水平上以计算出一个新的价值，最后将该价值与第t天的期权价值做差，分解出该单因素变化所带来的期权价值变化值。随后将三个因素的影响都进行分解后，本研究分别对每日期权价值、市场价格的总变动值和三个分量所带来的变动值用Eviews进行回归，通过回归系数与其显著性的对比做出进一步分析。

3.1 深度实值原油期权的市场价格与价值偏离分析

3.1.1 深度实值原油期权市场价格与期权损益的对比

对于深度实值原油期权，本研究对比了期权损益和与期权价格（见图10、图11）。

从以上两图可以发现，期权损益线与深度实值期权价格线几乎重合，说明对于深度实值的期权，市场几乎仅对期权的内在价值进行定价，而忽略了期权的时间价值，即期权收益上涨的盈利机會或下跌的损失风险。

因此，随着战争的爆发，标的资产价格波动率的上升，上海期货交易所深度实值的原油期权市场价格的被低估程度将会增加，因为该市场价格仅体现了期权的损益，即内在价值，而未体现出其他因素，如波动率、剩余到期期限等。

3.1.2 深度实值原油期权的因素分解分析

为了进一步做出分析，本文对深度实值的原油期权做了因素分解并进行回归（见表1、表2）。

其中，SP5表示sc2204C500因标的资产价格变动所带来的价值变动，V5表示sc2204C500因波动率变动所带来的价值变动，T5表示sc2204C500因剩余到期期限的缩短所带来的价值变动。

由表1、表2可见，两回归方程均具有接近于1的经调整的可决系数（Adjusted R2），说明两回归方程的拟合效果较好。在对价值变动值回归的回归方程中，三个变量所对应的系数p值均小于0.05，表示三个变量的影响均显著不为0；然而在对实际市场价格变动值回归的回归方程中，仅有标的资产价格变动带来的影响所对应的系数显著不为0，印证了上述结论——深度实值期权仅反映了标的资产的价格，而未反映波动率和剩余到期期限所带来的影响，而且反映标的资产价格较充分，因市场价格回归方程系数与价值回归方程系数较接近。

3.2 非深度实值原油期权的市场价格与价值偏离分析

3.2.1 非深度实值原油期权的因素分解分析

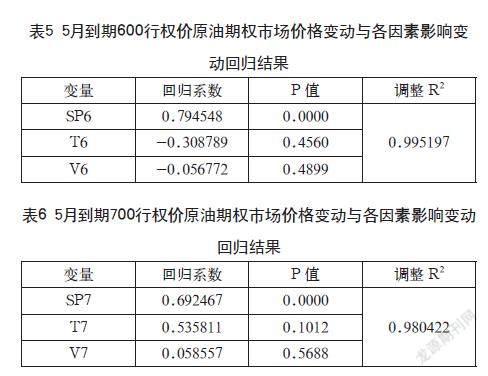
因4月到期的原油期权接近到期日，剩余到期期限因素影响不断扩大，期权的市场价格和价值均趋近于内在价值，使得前文现象的出现是由该因素直接导致（如图3接近到期日时期权价值相比市场价格加速下跌，可能是由于剩余到期期限因素将两者均拉至其内在价值而出现该现象）。然而根据上文的结论，几乎在所有波峰处都有市场价格与价值偏离现象的发生，因此为了剔除剩余到期期限因素的影响，本研究选取sc2205C600和sc2205C700期权，并直接采用因素分解并回归的方法进行了分析（见表3至表6）。

其中，SP6、SP7分别表示sc2205C600和sc2205C700因标的资产价格变动所带来的价值变动，V6、V7分别表示sc2205C600和sc2205C700因波动率变动所带来的价值变动，T6、T7分别表示sc2205C600和sc2205C700因剩余到期期限的缩短所带来的价值变动。

在表3和表4中，三个变量系数均显著不为0且经调整的可决系数（Adjusted R2）十分接近1，因此该回归方程拟合度非常好。本研究将这两个回归方程作为参照以分析深度期权价值在大幅上升与下降过程中变化程度大于市场价格变化的原因。

在表5和表6中，波动率与剩余到期期限所对应系数的p值均大于0.05，说明这两个变量的变动均不会对期权总体价值的变动产生显著的影响，而回归方程经调整的可决系数（Adjusted R2）仍十分趋近于1，说明回归方程对两期权实际市场价格的变化有很好的解释力度。

然而，通过表3、表4中sp6、sp7所对应的系数和表5、表6中sp6、sp7所对应的系数可以发现，在对价值变动值回归时，现货价格变动所带来的价值变动对应的系数均接近于1，而在对实际市场价格变动值进行回归时，sc2205C600与sc2205C700对应的该项系数分别为0.794548与0.692467，远小于参照组中的系数1。

由此可见，期权的实际市场价格中并没有完全反映标的资产价格变动理应带来的期权价值变动，因此导致期权市场价格在上升趋势中上涨量会明显小于价值上涨量，而在下降趋势中下跌量会明显小于价值下跌量。

3.2.2 下跌趋势中原油期权价值与价格偏离程度扩大的现象及其原因

上述结论并非在所有例子中都能得到证实，即期权在下跌趋势中价值的下跌量并非总是大于价格下跌量。由图6至图8可以观察到，在开始下跌的时点上（如2022年3月10日），期权的价值与市场价格更趋向于平行变化，或价值的变化量会小于市场价格的变化量（本文此处只观察5月到期的原油期权，因4月到期的原油期权临近到期日，剩余到期期限因素影响程度大幅增加，从而会影响在该问题上的判断）。通过上文对实际市场价格变化量与各分离因素变化量的回归结果（见表5、表6）可知，市场价格对波动率的变化定价并不显著。在期权价值开始下跌时，标的资产的波动率显著升高，标的资产价格的下跌使期权的价值也下跌，但期权价值会对波动率的变化定价，波动率的增大导致了期权价值的上涨，最终使波动率升高带来的期权价值上涨抵冲了一部分或全部的由标的资产价格下跌给期权带来的价值下跌，因此期权价值开始下跌时会出现与之前结论不相符的地方。

3.3 战争与非战争时期回归方程的对比

为了探究是不是战争因素导致了原油期权市场价格未充分反映标的资产价格的变化，本研究分解了sc2205C600原油期权2022年2月10日至2022年3月15日三个因素对其价值的影响量。后以2022年2月24日为分割点，将2022年2月10日至2022年2月23日分为一个样本，该样本代表战争发生前；将2022年2月24日至2022年3月15日分为另一个样本，该样本代表战争发生后，以这两个样本分别对期权市场价格变动量与三个因素所带来的变动量进行回归（见表7、表8）。

其中，SP表示sc2205C600期货合约因标的资产价格变动所带来的价值变动，V表示sc2205C600期货合约因波动率变动所带来的价值变动，T表示sc2205C600期货合约因剩余到期期限的缩短所带来的价值变动。

结果表明，两回归方程均有较好的解释力度，而且两方程仅有标的资产价格变动带来的影响所对应的系数p值小于0.05，表明该系数显著不为0，而其他两个解释变量所对应的系数均不显著。这两个回归方程的SP所对应的系数极其接近，表明战争的爆发并没有对市场价格反映各因素变动的充分程度有所影响。

4 结语

本文借助俄乌冲突背景下影响期权的各因素产生效应被放大的机会，发现了上海期货交易所原油看涨期权价格偏离价值的问题并剖析了其产生的原因。研究结果表明，我国上海期货交易所深度实值原油看涨期权的市场价格一直处于被低估的状态，其仅反映了期权的内在价值却忽略了時间价值。随着战争的爆发，原油价格产生大幅波动，各原油看涨期权的市场价格会在上涨时被低估或增加被低估的程度，而在下跌时缩小其与价值偏离的程度，并在波峰附近产生最大偏离。通过对期权每日价值变化量进行分解并进行相应的回归分析，本文发现主要有两个原因导致市场价格与价值偏离现象：一方面，原油期权的市场价格不对标的资产价格波动率变化及剩余到期期限的变化产生显著反应；另一方面，原油期权的市场价格未充分反映标的资产价格变动所带来的影响，并且该程度随着期权虚值程度的增加而增加。这种不充分与不反应是上海期货交易所原油期权市场价格本身固有的，而并非俄乌冲突带来的。当极端事件发生导致原油价格快速上涨或下跌从而使期权价值与市场价格都发生变化时，原油期权价值的变化量会明显大于期权市场价格的变化量，尤其是对于非深度实值期权。因此，这会使原油期权市场价格较大幅度地偏离其价值，最终在波峰附近偏离程度达到最大，并且这种偏离会随着期权虚值的程度增加而变得更加明显。

参考文献

Engle R F. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation[J]. Econometrica： Journal of the econometric society， 1982： 987-1007.

Bollerslev T. Generalized autoregressive conditional heteroskedasticity[J]. Journal of econometrics， 1986， 31（3）： 307-327.

Nelson D.B. Conditional Heteroskedasticity in Asset Returns： A New Approach[J]. Econometrica，1991（59）：347-370.

Zakoian J.M. Threshold Heteroskedastic Models[J]. Journal of Economic Dynamics and Control，1994，18（4）：931-944.

王沼锡.基于GARCH族模型的沪深300指数波动性模拟研究[J].中国商论，2022（1）：100-102.

Stentoft L. Assessing the least squares Monte-Carlo approach to American option valuation[J]. Review of Derivatives research， 2004， 7（2）： 129-168.

Robert C.Merton.连续时间金融[M]. 郭多祚，译.北京：中国人民大学出版社， 2013.

王军， 邵吉光， 王娟， 随机过程及其在金融领域中的应用（第2版）[M].北京：清华大学出版社、北京交通大学出版社， 2018.

Agustini W F， Affianti I R， Putri E R M. Stock price prediction using geometric Brownian motion[C]//Journal of physics： conference series. IOP Publishing， 2018， 974（1）： 012047.

Postali F A S， Picchetti P. Geometric Brownian motion and structural breaks in oil prices： a quantitative analysis[J]. Energy Economics， 2006， 28（4）： 506-522.