基于时频分析的跳频信号参数估计研究

张 玮,王 平

(1.海军工程大学， 武汉 430000; 2.解放军92038部队， 山东 青岛 266041)

1 引言

跳频[1-3](frequency hopping,FH)通信属于扩频通信的一种，跳频信号可以在较宽的带宽内随时间按伪随机规律跳变，具有突出的抗干扰、抗截获、抗多径能力，因而在军事领域和民用领域应用广泛。在通信对抗领域中，对跳频通信实施高效通信干扰的前提获取跳频通信信号参数，而如今用频设备日益增多，电磁环境日趋复杂，获取跳频通信信号参数也变得更加困难，因此对跳频信号参数估计逐渐成为通信对抗领域研究的热点问题[4]。

目前，用于跳频信号参数估计的方法主要有3类，图像处理法[5-6]，稀疏重构法[7-8]，时频分析法[9-11]，而目前时频分析法是跳频信号分析的主要方法。时频分析法是通过时间和频率2个变量来描述在不同时间条件下不同频率的信号能量强度的方法[11]。文献[12]提出一种基于平滑伪维格纳分布的参数估计方法，具有较高的精度，但是存在交叉干扰。文献[13]提出一种基于小波分解和希尔伯特黄的跳频检测算法，但是小波算法的低频部分分辨率较低，各频率分量强度并不相同，不便于进行阈值分割。文献[14]提出一种同步压缩的方法，通过对时频频谱进行压缩得到新的时频频谱，但是存在噪声鲁棒性差的缺点。文献[15]提出一种慢跳频信号的检测方法，根据各信道辐射计检测结果判断是否存在跳频信号，其缺点是抗噪性能差。文献[16]提出了一种根据信号和背景噪声频域自相关统计量检测的算法，但是这种算法只能在背景噪声中完成跳频信号检测，在存在其他干扰时算法失效。文献[17]提出一种跳频周期估计的方法，通过对时频矩阵中信号强度最大值的提取得到周期性函数，对函数进傅里叶变换运算，得到的峰值频率即为跳变速率，取倒数得到跳频周期的估计值，但是当存在定频信号干扰时算法性能大幅度下降。文献[10]通过提取时频脊线的方法进行参数估计，利用迭代法去除噪声，通过k-means聚类的方法进行参数估计，抗噪声性能较好，但无法解决定频信号与跳频信号发生频率碰撞的问题。文献[18]改进能量对消的方法，能够在完成对跳频和定频信号检测的同时减少计算量，但是在突发干扰和低信噪比的情况下性能较差。

为解决以上问题，本文提出一种基于时频分析的算法。通过短时傅里叶变换得到时频图像，利用能量对消去除定频信号干扰，采用全局阈值法对图像进行二值化处理，通过形态学滤波消除各类干扰，然后，通过对时频脊线中频率跳变时刻处理获得跳频周期的估计值，通过k-means聚类算法实现对频率集的估计。设计仿真实验并通过实测数据测试算法可行性。

2 跳频信号数学模型

跳频信号的频率可随时间伪随机跳变，其数学模型可进行如下定义[19-20]：

(1)

(2)

其中:T1为起跳时刻；Th为跳频周期；fk为第k个跳频时隙的跳频频率；N为观察时间内频率跳变数量；rectTh为门函数，其定义如式(2)所示。

3 跳频信号特征参数估计方法

算法具体步骤如下：

1) 采用短时傅里叶变换对信号进行时频变换，得到时频图像；

2) 采用能量对消的方法消除定频信号干扰；

3) 采用全局阈值的方法处理时频图像，得到二值化图像，其中阈值的计算采用OTSU算法；

4) 采用形态学滤波的方法去除信号毛刺、扫频干扰以及猝发信号干扰，弥合裂缝、填补空洞，获得高清晰度的时频图像；

5) 画出时频脊线，通过对频率跳变时刻求解一阶差分方程，可以获得跳频周期的估计值；采用k-means聚类算法，将频率值的聚类结果按照时间顺序进行排列，可以获得频率集的估计值。

算法总体流程框图如图1所示。

图1 算法流程框图

3.1 时频变换

通过时频图像对跳频信号进行分析是参数估计的效手段之一[21]，时频图像可以清晰地表示跳频信号的频率跳变情况。常见的时频变换方法有STFT、Wigner-Ville分布、平滑伪Wigner-Ville分布、小波变换、希尔伯特黄变换等。本文采用短时傅里叶变换(STFT)进行跳频信号的时频变换，即：

(3)

式(3)中:s(t)表示要处理的信号;h(t)表示窗函数;h*(t)表示窗函数的共轭函数。

为方便计算机计算，可将信号离散化处理：

3.2 能量对消

将时频矩阵与频率分量相减，可以得到对消矩阵I(n,k)：

由于在接收信号时间段内，定频信号始终存在，因此定频信号的时频能量特征随时间变化不大；跳频信号的频率随时间变化较快，每一频率在观测时间内存在时间较短，因此其对应频率上的均值远小于其能量值，因此采用对消的方法可以有效去除定频干扰保留跳频信号。

3.3 二值化处理

为获取清晰地时频图像，可将对消矩阵进行二值化处理，如式(4)所示，遍历对消图像矩阵，大于阈值μ则赋值为1，小于等于阈值μ则赋值为0，即可得到二值化图像矩阵。

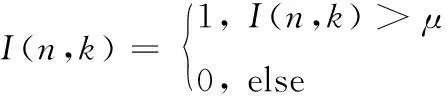
(4)

对于阈值的选取有多种算法，OTSU算法[23]、Bernsen算法[24]、Niblack算法[25]等，本文采取最大类间方差法(OTSU)进行图像二值化处理，OTSU算法属于全局阈值法，是一类基于整个图像通过计算选取合适的阈值的方法[26]。

通过OTSU算法计算阈值通常需要两步：

1) 计算图像灰度均值，选取阈值L∈[0,255]，小于等于L的像素点所占比例为w0，均值为u0；大于L的像素点所占比例为w1，均值为u1，则图片的灰度均值u为

u=w0×u0+w1×u1

其中p(i)为灰度为i的像素所占比例。

2) 计算类间方差：

u(L)=w0×(u0-u)2+w1×(u1-u)2

(5)

式(5)中，分别取L∈[0,255]，当u取最大值时，分离效果最好，此时的L值为最佳阈值。

3.4 形态学滤波

二值化处理后的图像仍然存在一些干扰信号，如扫频信号、突发信号以及未清除干净的噪声点，在图像上表现为孤立的或与有用图像相连的点或线，可以通过形态学滤波进一步清除干扰，提取有用信号。形态学滤波的主要运算包括腐蚀、膨胀、开运算和闭运算，通过设定结构元素消除图像中的孤立点以及填补空洞[27-28]。开运算为先腐蚀运算、再膨胀运算，可定义为：

I1(n,k)=I(n,k)∘b=(I(n,k)⊕b)⊙b)

(6)

式(6)中:I(n,k)表示待处理图像的时频矩阵; ∘ 表示开运算; ⊙表示膨胀运算; ⊕表示腐蚀运算;b表示结构元素。

闭运算为先膨胀运算、再腐蚀运算，定义为

I1(n,k)=I(n,k)·b=(I(n,k)⊙b)⊕b)

(7)

式(7)中，·表示闭运算。

在运算过程中结构元素起到重要作用，需要保留的图形要大于结构元素，需要消除的图像要小于结构元素。本文中形态学处理流程如下：

1) 构造小尺寸矩形元素，对时频矩阵进行闭运算，用以弥合裂缝、填充空洞。本文中矩形元素尺寸为3×80。

2) 构造水平的线形结构元素，对图像进行开运算，用以消除扫频和突发信号的干扰，从而完成形态学滤波处理。用于降噪处理的线性结构元素尺寸可以适当放大，应大于矩形元素的水平尺寸，小于跳频信号每一簇的水平尺寸，因此本文中构造的线形元素尺寸为400，能够有效保留跳频信号、去除孤立的噪声点和扫频干扰。

3.5 参数估计

3.5.1跳频周期估计

提取完成形态学滤波的时频图的频率脊线，对其进行修正，即可获得跳频信号的跳频图案。提取频率跳变时刻，组成新的数组：

T={T1,T2,T3,T4,…,Tn}

对该数组求一阶差分方程，可以得到新的数组，为各频率持续时间的估计值，对新的数组求尾切平均数，即除去最大值和最小值求均值，即可得到跳变周期的估计值。

3.5.2频率集估计

通过k-means聚类算法[29-31]，可以完成对跳频频率的估计。

聚类算法首先要预估聚类数量，在上一步中，可以通过跳变次数完成对聚类数量的估计，将图像点集划分为k个集合Z={Y1,Y2,Y3,…,Yk}，构造目标函数:

(8)

式(8)中:Ci为聚类i中所有点集的均值；Xj为聚类i中的点；Ni为聚类i中点的个数。

当均值与聚类中心不一致时，均值代替成为新的聚类中心，继续计算，直至均值与聚类中心相等，此时均值的频率坐标即为跳频频率估计值。

4 仿真实验

在高斯白噪声的条件下，产生的跳频信号，信噪比为-1 dB，采样率为1 000 kHz，仿真频率集[100、150、300、400、200、450、350、470、300、200]kHz，信号长度为100 000点。干扰信号包括两个定频信号，其频率分别为250 kHz和350 kHz，以及一个扫频信号，扫频范围为250～300 kHz，扫频周期为20 ms。其中350 kHz的干扰信号与跳频信号的其中一个频点相重合。

图2为通过对信号进行短时傅里叶变换产生的时频图像，窗函数为长度225的Hamming窗，在图像中可以清晰得看到跳频信号和干扰信号的时频图谱。

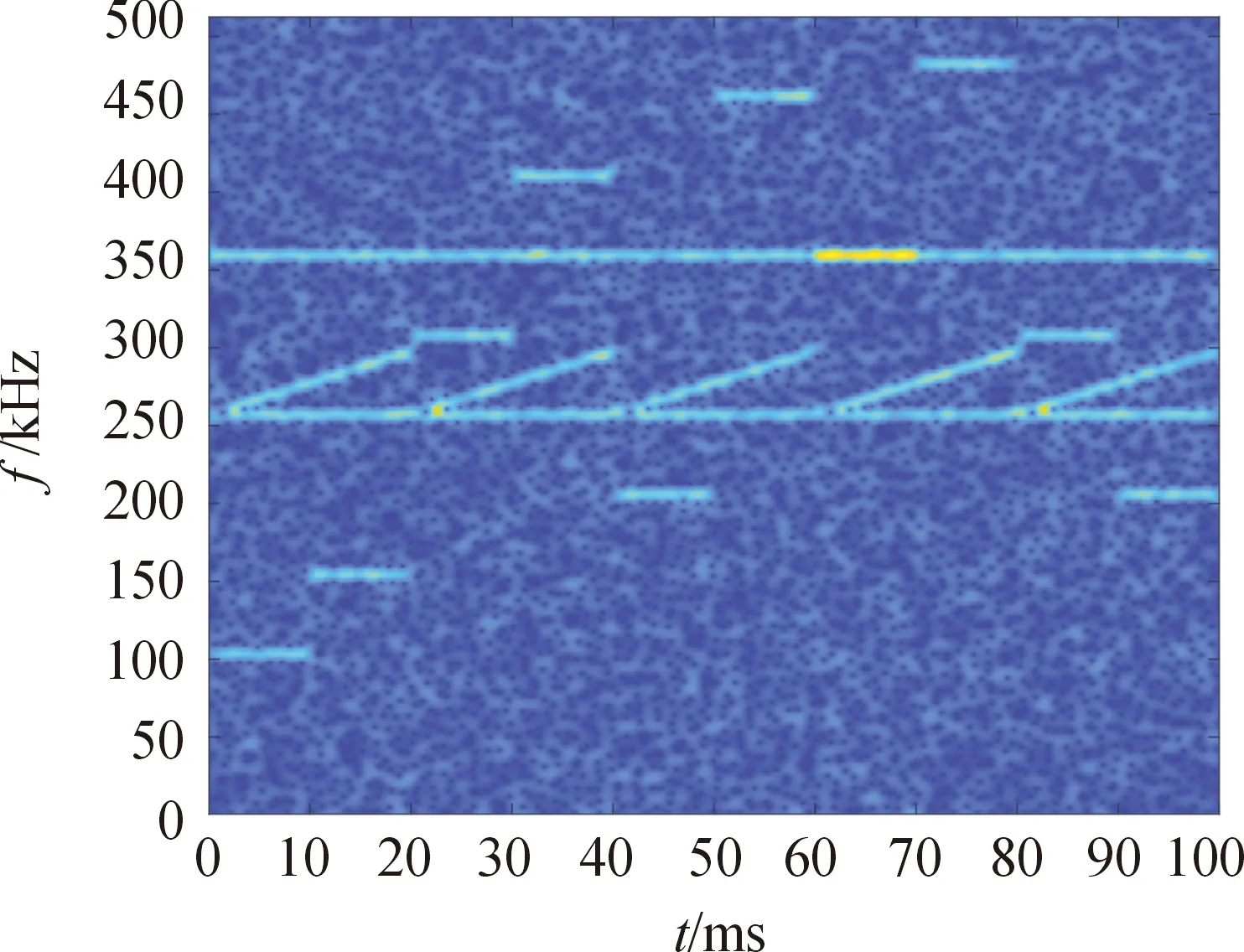
图2 接收信号的时频图像

图3为时频能量对消后的时频图谱，在图像中可以明显看到，定频干扰信号已经消除，而与定频干扰信号重合的跳频信号依然保留了下来。

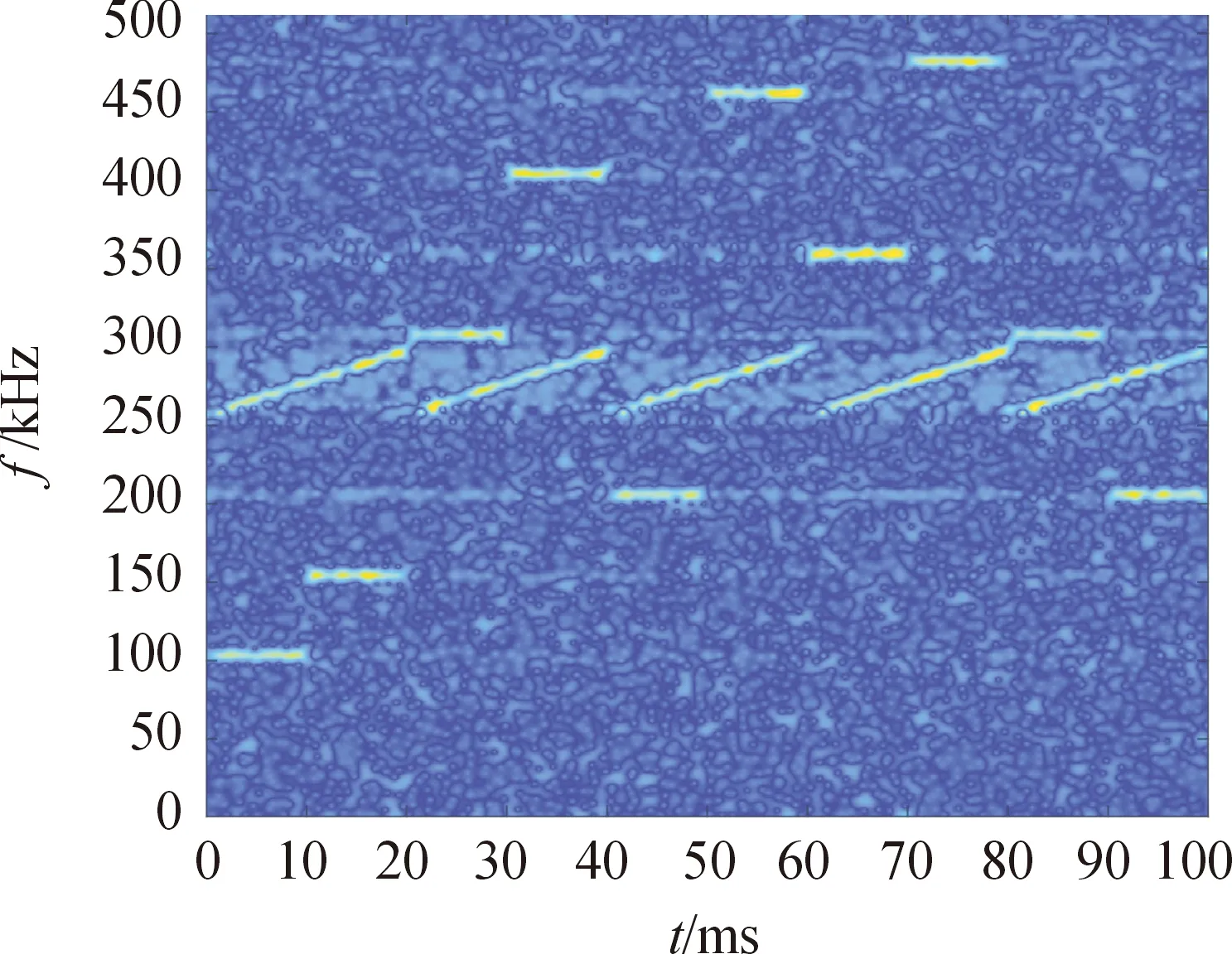
图3 对消后的时频图像

图4为二值化处理后的图像，经过全局阈值法能保留大部分信号能量，而大部分能量集中于跳频信号，因此处理后的二值化图像消除了大部分白噪声，保存了大部分的有用信号。

通过开运算、闭运算对二值化图像进行处理，可以有效去除扫频信号，去除突发信号，弥合细小裂缝，得到图5。提取脊线后得到的跳频图案如图6所示。

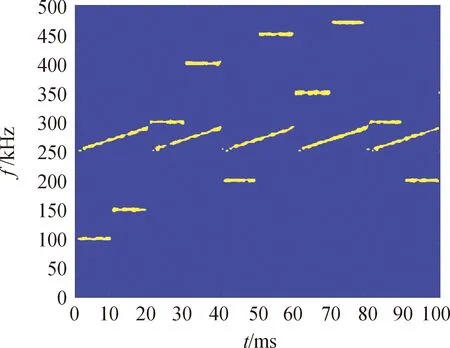
图4 二值化的时频图像

图5 形态学处理后的时频图像

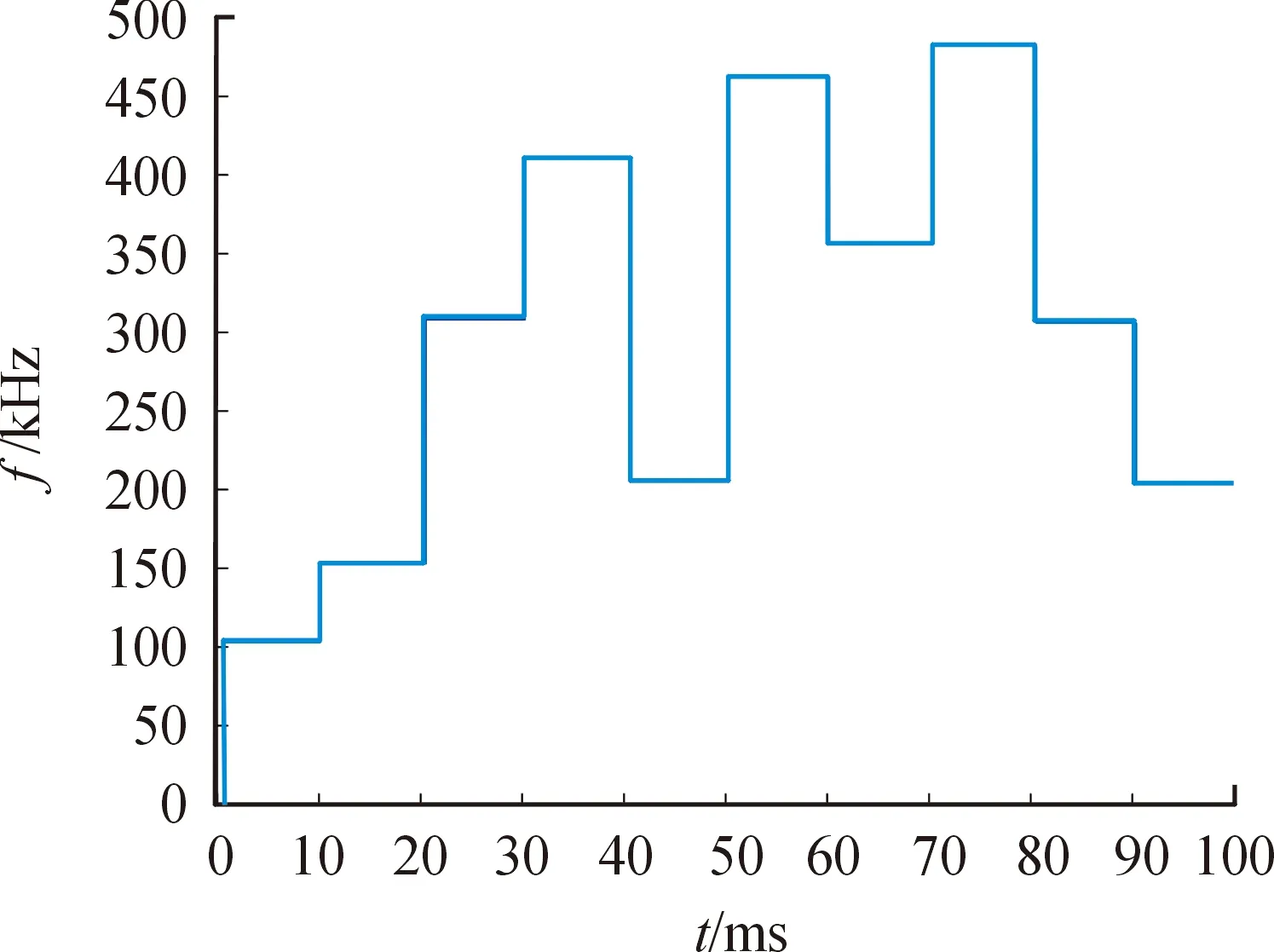
图6 跳频图案

为分析本算法的抗噪声性能，对测量误差进行如下规定：

(16)

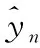
对本文的同一仿真信号分别在[-3,5]dB的信噪比条件下进行200次蒙特卡洛仿真实验，计算参数估计的误差。同时，分析在高斯白噪声、定频干扰和扫频干扰背景下本文算法与文献[5]和文献[10]的性能对比，其中图7为3种算法跳频信号频率集估计误差，图8为3种算法跳频信号跳频周期估计误差。

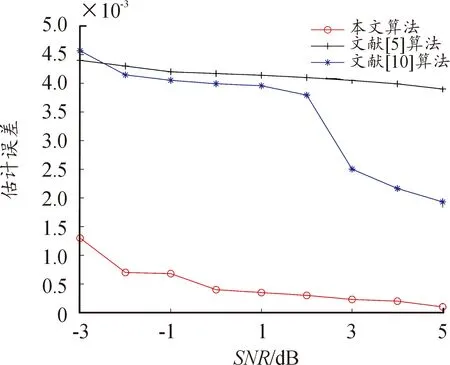
图7 频率集估计误差

图8 跳频周期估计误差

从仿真结果来看，本文算法明显优于2个对比算法。由图7可知：本文算法在跳频频率集估计与2个对比算法的估计精度在同一数量级上，但本算法有更高的精度；由图8可知，本算法在跳频周期估计误差总体在10-7数量级上，在信噪比大于-1 dB时，跳频周期估计性能有明显提升，取得了更好的效果。本算法可以消除各类干扰影响并在较低信噪比条件下完成跳频信号的参数估计，获得更高的估计精度。

5 实测数据分析

为验证算法实用性，采集大疆Mavic Air2型无人机遥控器信号进行算法性能验证。无人机的遥控器信号频段为2.4～2.486 GHz，信道带宽为2 MHz，信号采集采用USRP+GNU Radio平台的方式实现。由于硬件平台性能限制，最大采样率为50 Msps，因此采集信号前先通过频谱仪观察信号频率范围，再设置采样中心频率，以确保能够覆盖大部分信号。中心频率设置为2.42 GHz，采样率设置为50 Msps，截取567 005个数据点，时长11.3 ms的信号进行算法验证。

无人机遥控器实测信号的时频图像如图9所示，经算法处理后的时频图像如图10所示。

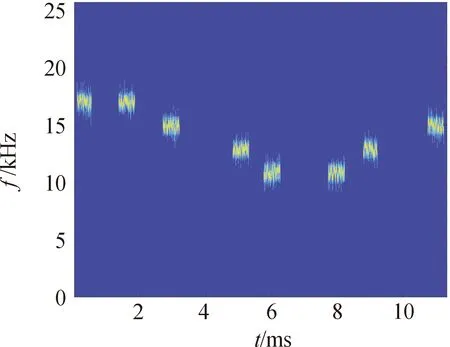
图9 实测信号时频图像

图10 经算法处理后的时频图像

对实测信号的参数估计结果如表1所示。由于实测信号的跳频周期可变，因此算法对跳频周期的估计失效。USRP对射频信号实施了下变频，得到的频率参数估计结果为基带信号频率，由于中心频率为2.42 GHz，将基带信号频率与中心频率相加，可以得到跳频信号频率估计值。

表1 实测信号参数估计结果Table 1 Estimation results of real signal parameters

各频率间隔约为2 MHz，符合说明书中对信道带宽的描述。通过实测数据测试验证，本算法可以实现跳频信号参数估计，具有实用性。

6 结论

本文提出一种基于时频分析的跳频信号参数估计算法，通过设计仿真实验检验了本算法能够在较低信噪比条件下具有较高的估计精度，通过实测数据的测试表明本算法具有实用性。