基于STK_Matlab的共形相控阵对卫星可见性分析

武昭希，吴 涛，吴海洲，孔永飞，史鹏程

(1.中国电子科技集团公司 第54研究所，石家庄 050081; 2.中国人民解放军61768部队，海南 三亚 572099)

0 引言

近年来，我国航天事业迅猛发展，在轨运行的卫星越来越多，根据celestrak网站提供的太空卫星数据，截至2022年11月20日，中国在轨运行卫星数量达到三百多颗，包括高分、风云、北斗、遥感、环境、海洋、实践、试验、资源等系列卫星。近年来中国卫星发射进入密集期，预计十四五末地面测控网要应对600～800颗在轨重要价值卫星、成千上万颗低轨互联网卫星的测控管理需求，这给测控领域提出了更高的要求，现有航天地面测控资源恐难以满足未来庞大的测控需求[1]。

卫星测控主要是完成对卫星状态的监控，近年来我国大力发展卫星测控技术[2]。随着我国在轨运行卫星数量的不断增多，在轨卫星测控面临诸多挑战。第一，在我国大力发展航天事业的背景下，当前有限的航天测控资源难以满足其带来的海量测控需求[3]；第二，我国需要实现多卫星的同时测控与管理，并且要提升卫星测控的覆盖性与时效性，因此卫星测控管理在内容和技术难度方面都逐步加大[4]，对于精确度和波束切换的频度也提出了更高的要求。

为了满足对全空域下同时出现的多个卫星目标覆盖，传统的抛物面天线体制已不再适应航天测控地面系统的需求，如今相控阵体制逐渐占据主流应用，其中在全空域多目标需求下球面共形相控阵占据独特优势[5]。基于现有测控设备资源，有效利用基于共形相控阵的全空域多目标测控系统的波束资源变得越来越重要。

为了设计对球面共形相控阵测控系统的波束资源调度模型，基于现有的球面共形相控阵测控模型，利用Matlab编程控制STK的仿真方法，分析卫星对子阵面的可视情况，可作为相控阵阵面资源的合理分配的前期准备工作。

本文以目前中国在轨运行卫星为研究对象，研究实现了一种基于STK与Matlab互联的球面共形相控阵模型对卫星可见性仿真分析计算方法，该方法可直接使用Matlab控制命令快速构建卫星运行场景，并能够提取STK卫星位置数据导入Matlab进行进一步球面阵仿真，分析其可见性，为地面测控系统波束资源调度的设计提供参考。

1 地面站共形阵列布阵模型

1.1 地面站地点

地面站的站址选择要考虑诸多因素，如地理位置、站址环境、视野范围、电磁干扰、地质和气象条件等，还要进行实地勘察和收测，最后选定最佳站址。

假定以石家庄某地区为地面站所在点，站址经度37.920 047 269 6°，纬度114.594 100 447 3°，高度41.76。

1.2 共形阵列布阵模型

目前合适的阵列结构多数都是半球形状的，总体上分为三类：

1)多个平面子阵拼成的半球面阵列，文献[6]提出了顶部截面为金字塔形状的多面拼阵模型，并给出了全空域覆盖下的最小化的阵面扫描角δ以及阵面倾角α的计算过程，且将天线共形在车体架构上。它的优点是扫描范围覆盖全空域，与球体形状的阵列相比，平面阵技术更加成熟，且工程建设的实现难度和运行维护的复杂度都较低。但多面拼阵也有其局限性，比如要考虑空域的扫描范围和相控阵天线扫描带来的栅瓣，这都和布阵方式紧密相关；在同一时刻，仅有一个阵面来合成单个波束，即使理论上可以实现全空域覆盖，但随着波束滑动，在阵面转接处波束宽度会变大，并且增益也会发生一些波动[6]。

2)球面共形阵列，它的天线单元放置位置构成一个具有半球形状的表面，每个阵元的法线方向不同，能够实现全空域的扫描覆盖，且与多面拼阵相比，球面共形阵列所需的阵元数量能够减少约20%，展现出更大的瞬时带宽，具有更低的极化和失配损耗[7]，单纯就它的这些优点而言，理论上是地面站的最佳选择。但实际工程实现中，球面共形阵列要逼近球形就需要非常多的子阵数量，同时需要更多的阵元数量与通道数量，其波束形成的算法变复杂[8]，波束形成网络的制造和组装也比平面阵列困难得多，对生产工艺的要求也大幅提高，因此造价自然也更加昂贵。因而在实际情况下大型球面相控阵并未得到广泛应用。

3)单平面相控阵，主要依靠伺服系统的机械控制其方位和俯仰。平面相控阵的优点主要有波束快速扫描、波束形状捷变等，但是当扫描角度变大时不能很好地控制波束宽度，其会不可避免的增大，且增益也会随之减小。并且波束在转向上不如电波束灵活。

本文采用多平面拼阵和球面共形阵设计相结合的办法，保持整个系统结构在局部为平面而整体为球体，通过使用平面子阵构造天线阵列，然后再组装成半球体。该模型中共有134个小子阵面，分成八层，从上到下每层的小子阵数量为1、4、10、16、21、25、28和29，每个小子阵的阵元使用数量为3×3，单个阵元及安装间隙之和的长度为0.05米，即小子阵形状为边长0.15米的正方形，子阵之间的间隔取0.01米，根据椭球几何关系，正方形子阵的四个顶点均内接于光滑的半椭球体内，沿Y轴方向作投影后，最外侧小子阵的顶点内接于光滑的半椭球形内，椭球的长轴为1.1米，短轴为1米，如图1所示。

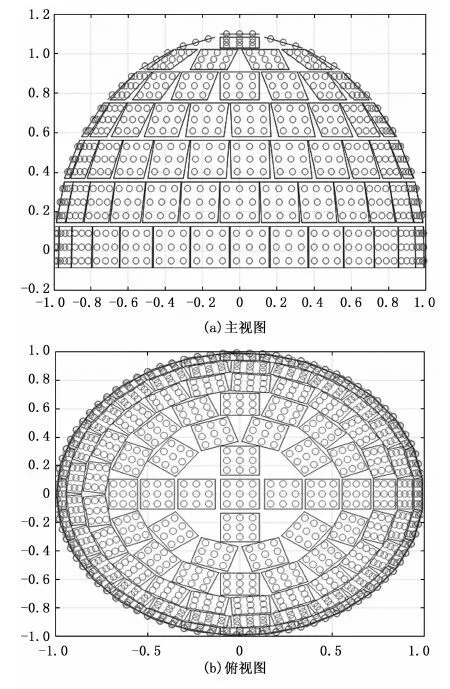
图1 共形相控阵模型

以上的参数设置是为了使阵列在全空域范围内增益平滑，因而让子阵均匀分布，并且子阵的间距也有效抑制了栅瓣。也可以根据实际需求调整参数改变布阵，比如可以通过增加短轴长度来使椭球拉高，进而改变每层子阵的倾角，或者为了让球阵整体降低仰角提高增益，可以将共形阵的下方一层或几层调整为垂直，并与上一层的阵面下边沿相连，呈半椭球加柱面阵的结构，也可以达到目的[9]。

2 可见性计算原理

2.1 坐标系定义与转换

地心惯性坐标系(ECI，earth-centered intertial frame)以地心为坐标系原点，z轴沿着地球自转轴指向协议地级，x轴位于赤道平面内，并指向春分点，y轴符合右手笛卡尔坐标系。ECI坐标系的坐标轴用上标i表示为xi，yi，zi。

地心地固坐标系(ECEF，earth-centered-earth-fixed frame)坐标原点位于地球地心，z轴与地轴平行指向北极点，与ECI坐标系不同的是ECEF坐标系随地球同步旋转，x轴指向赤道与格林尼治子午线的交点，y轴在赤道平面上与x轴和z轴构成右手笛卡尔坐标系。ECEF坐标系的坐标轴用上标e表示为Xe，Ye，Ze。ECI和ECEF坐标系如图2所示。

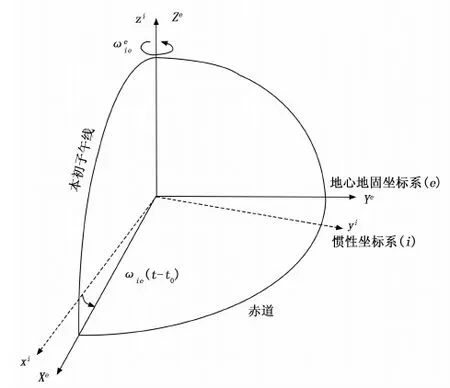
图2 ECI与ECEF坐标系

东北天坐标系(ENU，east-north-up frame),假设地球表面一点P，ENU坐标系原点就是P点，过P点作一平面与地球椭球面相切，在该面取正北方向为y轴，x轴指向正东，z轴指向法线方向。

要将ECEF坐标系转换到ENU坐标系,首先是将ECEF坐标系绕z轴旋转，旋转角度为λ+π/2，旋转矩阵为：

(1)

然后再绕x轴旋转，旋转角度为π/2-φ，旋转矩阵为：

(2)

所以从ECEF坐标系转换到ENU坐标系旋转矩阵如下：

Re2t=R2R1=

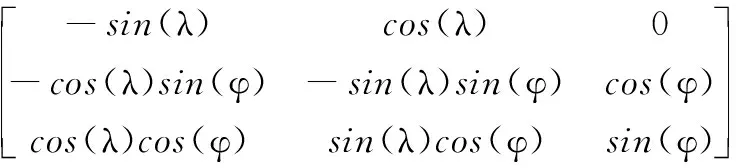
(3)

在共形相控阵测控系统中，主要参考以下两种坐标系：一种是以地面站站心为基准的站心直角坐标系与站心极坐标系，一种是以阵列阵面为基准的视线直角坐标系和其极坐标系。

本文在共形阵中所使用的站心坐标系即为东北天坐标系ENU，如图3。其中，r为目标到原点的距离；θ和φ分别为目标在站心直角坐标系中的俯仰角和方位角。

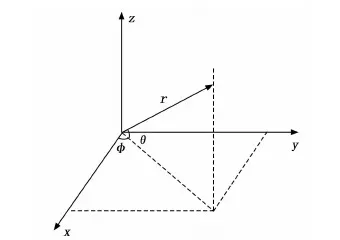
图3 站心坐标系

站心直角坐标系(x,y,z)与站心极坐标系(r,θ,φ)的关系如下：

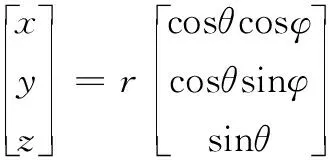
(4)

(5)

类比以上，视线直角坐标系与视线极坐标系用(x0,y0,z0)与(r0,θ0,φ0)表示。站心坐标系的x-y面与全空域扫描范围的水平面重合，视线坐标系的x0-y0面与各个子阵面重合。因目标符合在远场条件下，所有坐标系原点视为同一点。

将站心坐标系旋转就可以将站心坐标系转换到视线坐标系：站心坐标系的x-y面先绕z轴逆时针旋转，旋转的角度为该阵面所处的方位角β，再绕y轴旋转，旋转的角度为阵面倾角α，即得到该阵面所对应的x0-y0面。

旋转矩阵如下：

(6)

得：

(7)

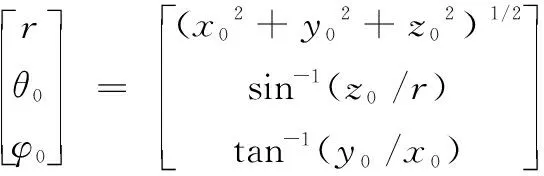
(8)

综上，由式(6)～(8)，以及阵面倾角α、方位角β及波束指向，就可得到对应指向在视线坐标系中的坐标。

2.2 卫星位置计算

在ECI坐标系下，卫星位置的计算公式为：

(9)

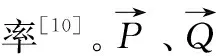
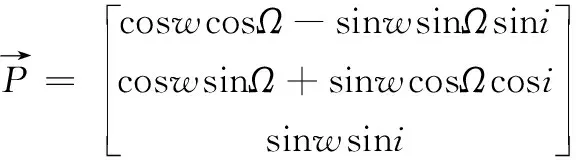
(9)

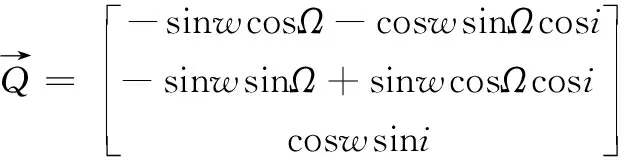
(10)

式中，w为近地点幅角，Ω为升交点赤经，i为轨道倾角。

2.3 地面站对卫星可见性计算

地面站可见范围如图4所示。

图4 地面站可见范围示意图

(11)

当多颗卫星同时运动，若卫星在空间上能够满足式(11)，则卫星可见。同时满足式(11)的卫星颗数，即为该时刻地面站可视的卫星数量。

(12)

式(12)中，N为同时看到的卫星颗数，因卫星运行和地球自转，N随着时刻变化而变化，对可见星取交集便可得到N。

由上可知，根据式(9)可得到所有卫星的位置矢量，根据式(12)便能得到地面站同时可见的卫星数目。

2.4 共形阵面可见性判定

共形相控阵的起作用阵元数量会随着来波方向变化而变化，因为要考虑全空域扫描时子阵间遮挡效应以及平面子阵的增益要求，因此在共形数字波束形成中，天线单元方向图应在未起作用的阵元处置零。本文所采用的共形阵面作用判定步骤如下：

1)根据坐标转换得到目标卫星的位置方向，即站心极坐标系下的方位角φ与俯仰角θ。

2)仿真计算布阵模型各子阵阵面倾角α和在站心直角坐标系中所处的方位角β。

3)再次进行坐标系转换。先通过式(5)将站心极坐标系坐标(r,θ,φ)转换到站心直角坐标系坐标(x,y,z)，再由式(6)的旋转矩阵得到式(7)中的视线直角坐标系坐标(x0,y0,z0)，最后通过式(8)得到各卫星对应于各子阵视线极坐标系下的方位角φ0与俯仰角θ0。

4)设定最大扫描角θmax，为了使平面子阵达到增益要求，通常取不超过60°。当θ0≥θmax时，各阵元起作用，否则阵元增益置零。

举例某时刻某个卫星位置方向在站心极坐标系中的方位角0°，俯仰角30°，子阵平面最大扫描角θmax取60°，判定效果如图5所示，黑色部分为该卫星来波方向下起作用的阵元。

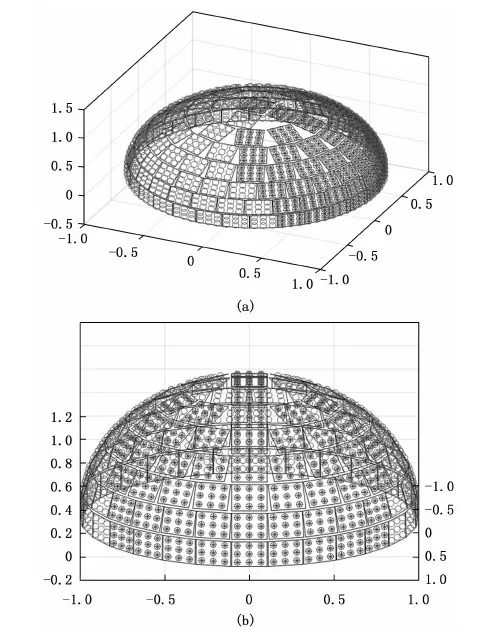
图5 对某可见卫星子阵作用判定效果图

在全空域的范围内考虑遮挡判定下，通过沿来波方向作投影的图5 (b)可以看出，投影面内各子阵边沿无重叠，相互之间无遮挡，参与作用的阵元之间没有出现间隔遗漏，证明在全空域范围内的作用判定方法可行有效。

3 STK与Matlab互联仿真

3.1 STK与Matlab简介

现如今越来越成熟的卫星仿真工具包(STK，satellite tool kit)由美国分析图形有限公司(AGI,analytical graphics, inc.)公司发明，它是一款在航天工业领域用于全过程仿真的商业分析软件，它的仿真场景具有可视化，动态化的特点，并可提供详细准确的文字、图表报告等多种分析结果，并且具有强大的分析、图形支持和大量数据参数输出功能。对于卫星的可见性分析等方面有着广泛应用，在时域和空域都能提供极其准确的专业分析。STK还具备成熟的互操作性，如和matlab软件的互联[11-13]。Matlab是目前在工程应用和数据计算方面最成熟的仿真分析软件，其具有先进的模块化的分析功能和数学计算功能。STK只能单步点击操作，在数据量大时，需要多次的重复操作。两款软件互联能够显著提高STK的计算分析能力，让两款软件优势互补，功能融合，从而极大地拓宽STK的应用范围[14]。

由上可知STK在场景建模方面存在一定的局限性，因而本文以我国某地地面测控站分析为例，利用Matlab和STK互联实现STK自动生成可视化场景和仿真数据的自动导出，对目标卫星的分布及可视情况进行仿真[14]。与单一STK建模相比，增加了Matlab的编程控制，大量数据能够循环计算，并且可以在Matlab中对数据进行二次处理，使得仿真分析更加便捷灵活。

3.2 卫星轨道分布

卫星星历用来描述卫星运动的位置和速度，它随时间变化，也叫两行轨道数据(TLE,two-line orbital element)[17]。

通过celestrak网站查询中国所有成功发射过的卫星，通过查看其运行状态可以得到中国目前在轨运行的366颗卫星的两行轨道数据。

整理获取的TLE数据，通过Matlab程序处理，将其导入STK场景中，就可以建立卫星轨道模型。

3.3 STK与Matlab互联仿真流程

STK和Matlab互联可以通过connector模块或者com口形式进行信息互通，com是微软公司提出的一种组件技术，它定义了对象在单个应用程序内部或多个应用程序之间的行为方式。

com客户端是任何代码或对象获取指向com服务器的指针，并通过调用其接口的方法来使用其服务。com服务器是向客户端提供服务的任何对象;这些服务采用com接口实现的形式，可由任何能够获取指向服务器对象上某个接口的指针的客户端调用。此外，com还提供一种机制，允许进程内服务器(DLL)在代理项 EXE 进程中运行，从而获得能够在远程计算机上运行进程的优势。

本文使用com的方法进行连接。Matlab编程代码通过com口控制STK，建立仿真场景，设置场景参数，并以1.1节中确定经度纬维度高度的固定地面站为观测中心，导入卫星TLE数据并循环创建卫星，进行可见性分析及其它场景数据处理，计算并获取access数据，最后结合布阵仿真子阵可见性。程序流程图如图6所示。

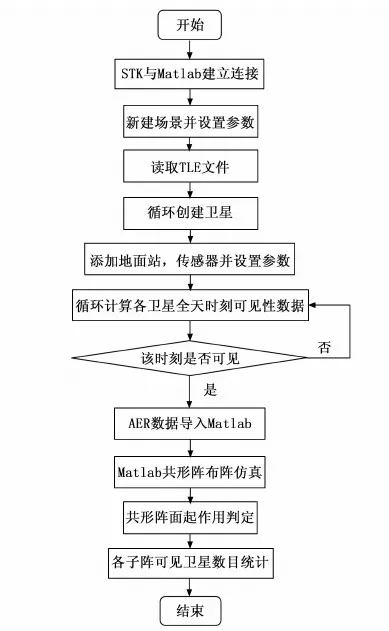
图6 STK与Matlab仿真流程图

1)获取运行中的STK实例句柄，然后使STK与Matlab建立连接，代码如下：

uiapp=actxGetRunningServe(‘STK11.application’);

root=uiapp.Personality2;

2)创建场景。如果未发现场景，则新建一个;如果发现打开的场景，弹出窗口询问是否保存关闭并根据设定的场景时间、步长参数重建一个场景，主要代码如下：

scenario.SetTimePeriod(strBegTime,strEndTime);

scenario.Epoch = strBegTime;

root.ExecuteCommand('Animate * Reset');

3)读取TLE的.txt文件，指定转换的卫星NORAD编号，循环读取轨道根数，并处理名字，核心代码如下：

tmpTLE.Name=[char(strName)'_'char(vecTLELine2(2))];

tmpTLE.Code=str2double(vecTLELine2(2));

tmpTLE.Line1=strTLELine1;

tmpTLE.Line2=strTLELine2;

4)循环创建卫星。根据读取处理的TLE数据，利用“SetState”命令循环创建卫星，该指令可以为STK的目标设置轨道、轨迹、路径，应用广泛。核心代码如下：

tmpSat=root.CurrentScenario.Children.New('eSatellite',char(strProSat));

strCommendTLE=['SetState*/Satellite/'char(strProSat)'TLE"'char(tmpStarTLE.Line1)'""'char(tmpStarTLE.Line2) '"'];

root.ExecuteCommand(strCommendTLE);

propagator = tmpSat.Propagator;

5) 添加地面站和传感器并设置参数，利用“AssignGeodetic”指令设置地面站经纬高，代码如下：

fac.Position.AssignGeodetic(37.920 047 269 6,114.594 100 447 3,41.76);

6)利用“ComputeAccess()”函数，循环计算所有卫星的全天时刻可见性数据，代码如下：

access = sensor.GetAccessToObject(tmpSat);

access.ComputeAccess();

7)利用“DataProviders”函数获取可见性数据，并存入Matlab元胞数组中，代码如下：

accessAER=access.DataProviders.Item(‘AERData’).Group.Item(‘Default’).Exec(scenario.StartTime, scenario.StopTime, 1);

accessaer=cell2mat(accessAER.DataSets.GetDataSetByName('Duration').GetValues);

8)进行共形相控阵的布阵模型仿真，具体参数详见1.2节；

9)判定各个子阵面是否起作用，卫星位置在子阵面的视线坐标系下俯仰角大于30°时，子阵起作用。

10)统计各子阵面可见卫星数量，储存数据，用作分析。

4 仿真结果分析

4.1 单子阵对卫星可见性分析

以单子阵可见卫星最多时刻为例。在STK中可以直观的看到卫星的位置分布，只保留显示该时刻可见卫星。图7为STK中可视卫星最多时刻的在轨卫星分布的3D图，图8为该时刻在轨可视卫星的2D图。

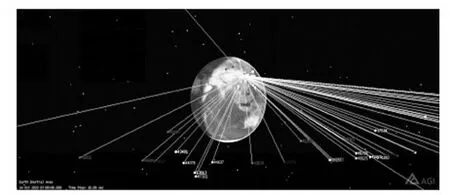
图7 中国在轨卫星3D图

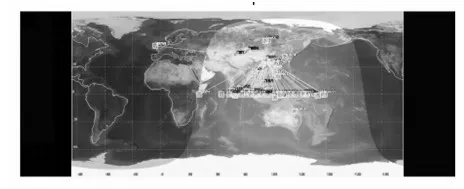
图8 中国在轨卫星2D图

该时刻地面站可见卫星69个，其可见星NORAD编号如表1所示。

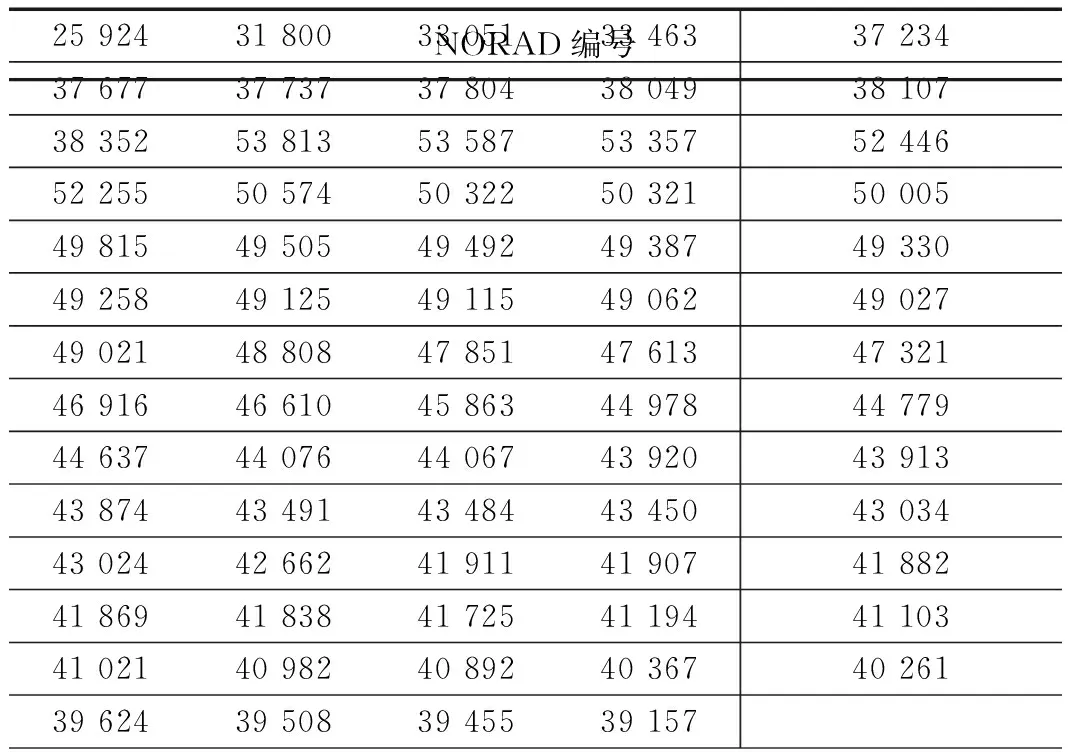
表1 地面站可见卫星NORAD编号

在该时刻，地面站共形球面阵各个子阵的可见卫星数量如图9所示。

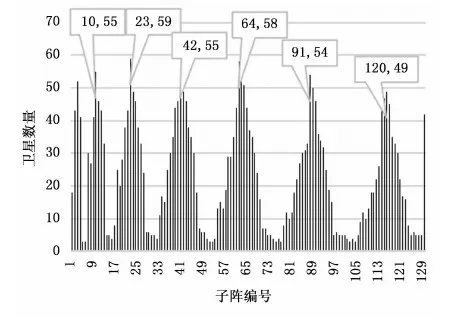
图9 各子阵可见卫星数量

图9统计结果表明：在偏离子阵面法线0～60角度卫星可见的情况下，可见星数量呈现出以子阵编号3、10、23、42、64、91、120为中心的峰值，其中以23号子阵所见卫星数量最多，达到59颗。

4.2 全子阵对卫星全天时刻可见性分析

同4.1，仿真并统计全天所有时刻球阵整体可见星数量，结果显示可见星数量在全天时段内分布较为平均，最少59颗，最多72颗，多数时间在65颗左右。然后仿真并统计全天所有时刻各子阵的可见卫星数量，在此以0时，3时，6时，9时四个时刻的单子阵可见星统计结果为例，如图10～13所示。

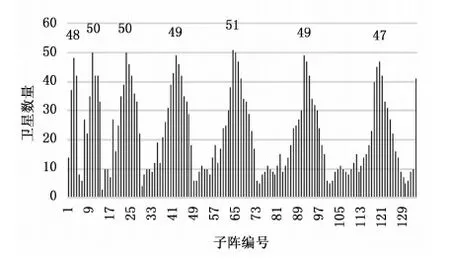
图10 0时各子阵可见卫星数量

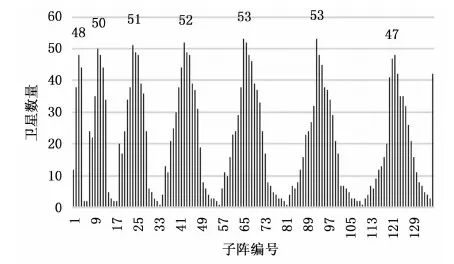
图11 3时各子阵可见卫星数量

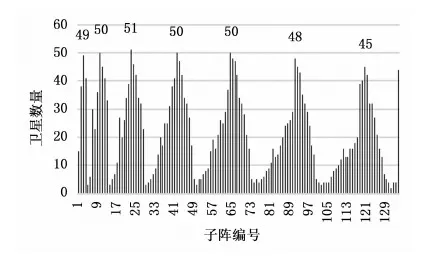
图12 6时各子阵可见卫星数量

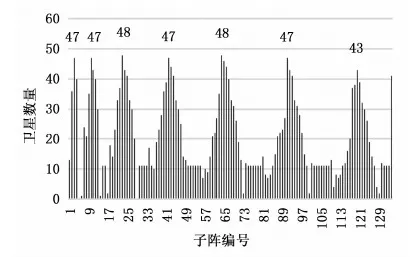
图13 9时各子阵可见卫星数量

在偏离子阵面法线0～60角度范围内卫星可见的情况下，全天时段各子阵可见星数量的柱线图分布近乎相同，都呈现出以子阵编号3、10、23、42、64、91、120为中心的峰值。

4.3 地面站测控需求分析

根据以上统计分析，针对卫星的测控需求，在可见星数量最多的时刻，地面站球面共形阵最多需要合成72个波束，单子阵最多需要合成59个波束；其中以编号3、10、23、42、64、91、120的子阵波束资源需求量最大。这几个子阵都在球阵的南部，说明可见卫星的分布在以地面站为中心的正南方向较为集中。

5 结束语

共形相控阵波束资源分配对于全空域多目标测控系统意义重大，对共形相控阵的卫星可见性分析可为其提供需求依据。STK与Matlab联合仿真能够使两款软件的优点融合，使得大量数据计算可以自动化完成，并能针对特定布阵进行地面站的可见性计算，从而实现高效、准确、快捷的互联式仿真分析。通过Matlab与STK的互联仿真，完成了对基于球面共形阵的地面站卫星可见性分析，得出了中国在轨卫星对于地面站的全时段分布情况和各子阵的波束需求，为共形相控阵波束资源调度设计提供参考。

本文研究尚有可拓展部分，一是只分析了球面共形阵对卫星可见的数量需求，可根据现有结果，继续按功能分类统计各个系列卫星的分布情况、按轨道高度不同的卫星的分布情况，以及特定测控任务的卫星分布情况；二是仅分析了单站卫星可见性，可以此为基础拓展研究卫星可见性和站址的关系，以及和布站数量，布站形式的有关问题，作为下一步工作研究方向。