典型工况下扭梁关键焊缝的可靠性优化研究

王巽， 张红业， 杨权， 何家兴

广州汽车集团股份有限公司汽车工程研究院，广东广州 511434

0 引言

近年来，扭梁悬架以其占用空间少、结构简单、安装定位便利等特点，被广泛应用于电动车后悬系统中。因其左右两侧车轮的运动存在耦合性，来自路面的激励传递至扭梁本体，使其受力形式较为复杂，且扭梁作为汽车后悬的主要承载件，其结构可靠性关乎行车安全，故扭梁关键焊缝的可靠性研究得到了人们的广泛关注[1-2]。

正交试验的相关理论最早由日本的统计学家田口玄一博士在20世纪40年代提出并进行实际应用。对比于全面试验的各试验方法，利用正交试验得到的结果包含了有效信息的同时显著地减少了试验的样本量。通过对试验结果进行统计学分析可以得出各因素对目标参数的影响趋势、各因素主效应排序、因素最优组合等[3]。

本文以某量产车型扭梁为例，使用ABAQUS软件对扭梁有限元模型进行典型工况(侧向力)下扭梁关键焊缝应力的数值模拟，并在单品台架下验证了该仿真模型的准确性，基于正交试验对扭梁结构设计参数进行优选，以扭梁关键焊缝在典型工况(侧向力、纵向力)下的疲劳寿命为评价指标，确定了扭梁结构参数的最优组合，以期为扭梁可靠性设计提供理论参考。

1 扭梁主要失效机制

一般来说，结构材料的强度极限越大，外加载荷应力水平越低，结构的疲劳寿命越长。扭梁本体多采用优质结构钢，在开发初期，研发人员不断地设计-仿真迭代使本体结构处于合理应力水平区间，在路面不平度的动态激励下，扭梁本体所受应力低于材料的屈服强度，处于线弹性应力-应变范围内，疲劳寿命一般大于1×105次，属高周疲劳范围。扭梁两侧用于安装车轮的拖曳臂之间由横梁刚性连接，当两侧车轮发生反向轮跳及受到侧向、纵向力时，横梁发生扭转、剪切及弯曲等变形，在扭梁所有焊缝中连接横梁与两侧拖曳臂的主焊缝受力最为严苛，易发生开裂、脱焊等失效，CAE仿真结果也说明了这一点，所以需要重点关注[4-5]。

扭梁复杂的使用环境使其受到的外部交变载荷呈随机性。目前，业内对于变应力幅值下结构疲劳寿命分析运用比较成熟的是线性疲劳累积损伤理论，即当零件受到幅值变化的疲劳载荷时，其疲劳损伤与载荷幅值所加载的顺序无关，只与受到的载荷相对幅值有关，并且总的疲劳损伤由所有疲劳载荷产生的疲劳损伤线性相加所得。其中Palmgren-Miner法则在业内最为经典且应用最为广泛，该法则认为：零件在受到变幅值的疲劳载荷作用时，将该载荷分解为多级不同应力幅值的载荷对结构起等效作用，通过疲劳损伤可累积的理论，当疲劳损伤的总和达到1时，结构发生疲劳失效[6-7]。

(1)

式中：L为变幅载荷的应力水平级数；ni为第i阶载荷的循环次数；Ni为对应第i级载荷下的疲劳寿命。

2 扭梁有限元模型建立与验证

扭梁有限元模型如图1所示。其中焊缝采用四边形单元模拟，扭梁与车身连接处建立CBUSH衬套单元，并赋予该单元实测扭梁衬套的三向刚度曲线，衬套与车身、扭梁与减震器、扭梁与车轮毂轴承连接部位采用RBE刚性单元模拟。为验证模型仿真的精度，搭建台架对扭梁施加侧向力工况以验算仿真值与实测值的相对误差。

图1 扭梁有限元模型

2.1 侧向力工况下扭梁主焊缝强度分析

根据扭梁侧向力台架实际受力情况，约束左、右扭梁车身连接处1～6自由度，在左侧轮心处施加-12 kN的水平侧向力，约束右侧轮心1～3自由度，运用ABAQUS进行该工况下的静强度计算，得到扭梁部分区域的Von Mises应力云图,如图2所示。

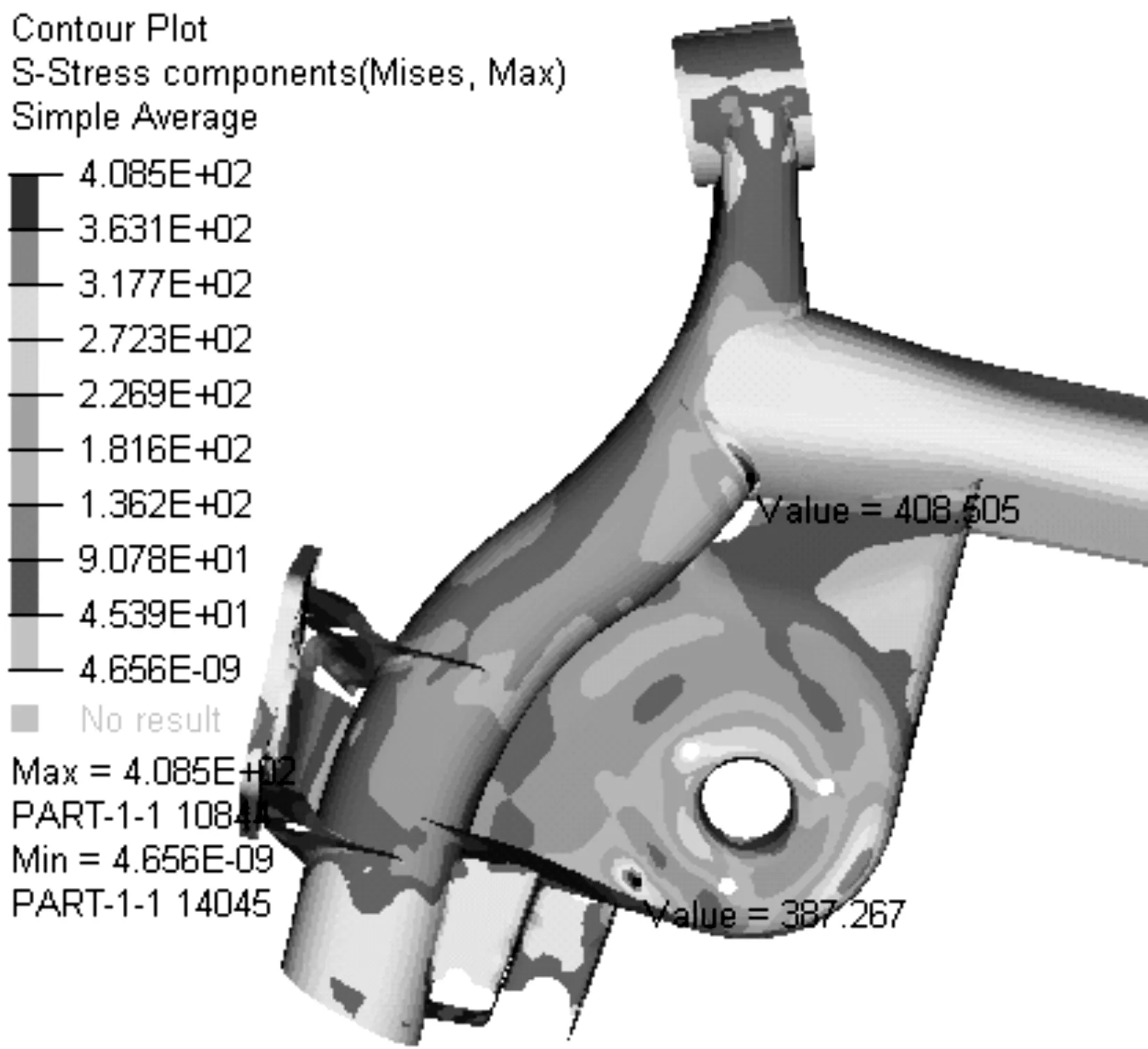
图2 -12 kN水平侧向力下扭梁部分区域的应力分布

根据分析所得到的应力分布云图可以看出，在横梁与纵臂搭接的主焊缝焊趾附近区域存在应力集中，最大应力值达到408.5 MPa。

2.2 侧向力台架验证

按照上文约束及加载方式搭建扭梁侧向力试验台架，鉴于焊缝处应力无法直接布点采集，可通过应力外推法进行焊趾附近热点应力验算。热点根据其所处位置可以分为“a”型热点、“b”型热点和“c”型热点，如图3所示，其中横梁与纵臂搭接主焊缝焊趾属于“c”型热点[8-9]。

图3 焊趾热点类型

由于焊缝附近应力分布非线性程度较高，应采用三点二次外推法，DNV规范建议取距离焊趾0.5h、1.5h和2.5h(h为纵臂壁厚)处为外推点，进行二次外推，具体的插值计算公式[10]为：

σHS=

(2)

式中:σHS为外推得到的焊趾处热点应力值；x1、x2、x3分别为外推点1、2、3与焊趾热点之间的距离；σs(x1)、σs(x2)、σs(x3)分别为外推点1、2、3处的结构应力值。

采用中航电测的三轴直角电阻应变花BE120-3CA对3个推点进行贴片，其中应变花0°应变片平行于焊缝，90°应变片垂直于焊缝布置，数据采集分析采用TST3827E系统，应变花布置位置如图4所示。

对3个外推点各通道采集的应变值换算成该点所受的最大主应力值，计算公式[11]为:

(3)

式中:E为钢弹性模量；μ为泊松比；ε0°、ε45°、ε90°分别为0°、45°和90°应变片采集的应变值。

根据实测数据，推算扭梁在-12 kN水平侧向力下该处焊缝的热点应力值为392 MPa，CAE仿真数据与试验实测结果误差为4%，且CAE模型结果偏于保守，经判断可以应用于关键焊缝的可靠性分析研究。

3 扭梁关键焊缝可靠性结构设计正交试验的优化

3.1 正交试验

经分析，影响扭梁横梁与纵臂搭接主焊缝疲劳寿命的主要结构因素有横梁壁厚、纵臂壁厚、是否设置横梁与纵臂间的加强支架及加强支架所处位置、弹簧托盘在横梁搭接型面与主焊缝距离等，由于改变横梁壁厚会影响扭梁扭转刚度进而影响后悬K&C性能，本文挑选另外3个影响因素设计正交试验表，以某已量产车型结构为基准设置4个因素水平：纵臂厚度h∈[3.2,4.0]mm，加强支架所处主焊缝位置如图5所示，弹簧托盘在横梁上的搭接型面末端与主焊缝距离如图6所示。因素A、B、C分别对应纵臂厚度、加强支架及所处位置和弹簧托盘在横梁搭接型面与主焊缝距离，假设这3个因素间不存在交互影响，设计进行3因素4水平的正交试验，具体见表1。

图5 加强支架所处主焊缝位置

图6 弹簧托盘在横梁上的搭接型面末端与主焊缝距离

表1 因素水平

选择3因素4水平正交表设计方法，共16组试验，模拟整车制动和转向两个典型工况，约束左右两侧扭梁与车身连接点1～6自由度及单侧轮心1～3自由度，在另外一侧轮心加载±12 kN侧向力及±12 kN纵向力，以两个工况下横梁与纵臂搭接主焊缝疲劳寿命为优化目标，调用nCode标准材料库中典型焊缝S-N曲线对所有组合主焊缝焊趾附近区的疲劳寿命进行模拟计算，获得区域内最小疲劳寿命值，正交试验结果见表2。

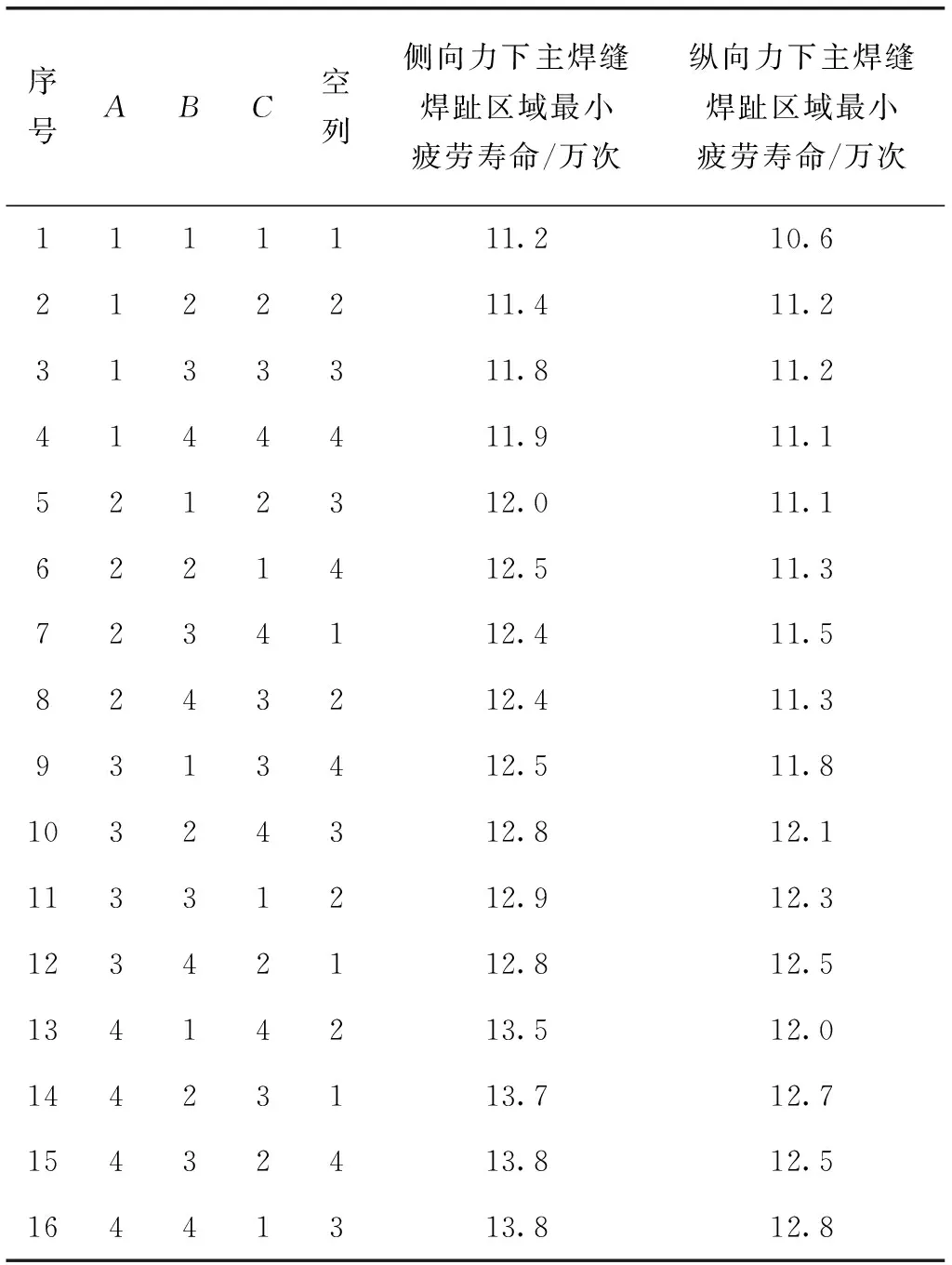
表2 正交试验结果

首先按照单一指标的分析方法分别对两个优化目标进行极差分析，优选出两者各自的最优组合，再对两组优选结果进行综合分析，得到最终的优化组合。

3.2 试验数据分析

根据正交试验表中各组合方案的仿真计算结果，得到各个影响因素的极差，结果见表3。表中ki代表因素在第i水平试验评价指标的平均值，极差R为各因素每一列ki的最大值减去最小值。根据统计学理论，极差的相对大小反映了各个因素对试验结果的影响程度，极差越大，表示该因素对试验结果的影响越明显[12]。根据分析的结果绘制各因素对试验结果的影响趋势，如图7所示。

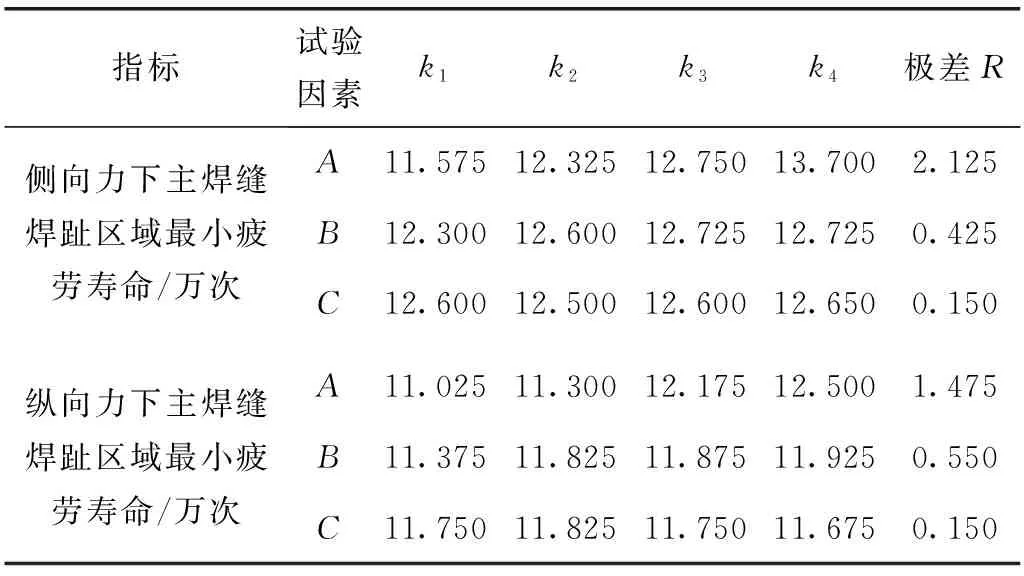
表3 极差分析结果

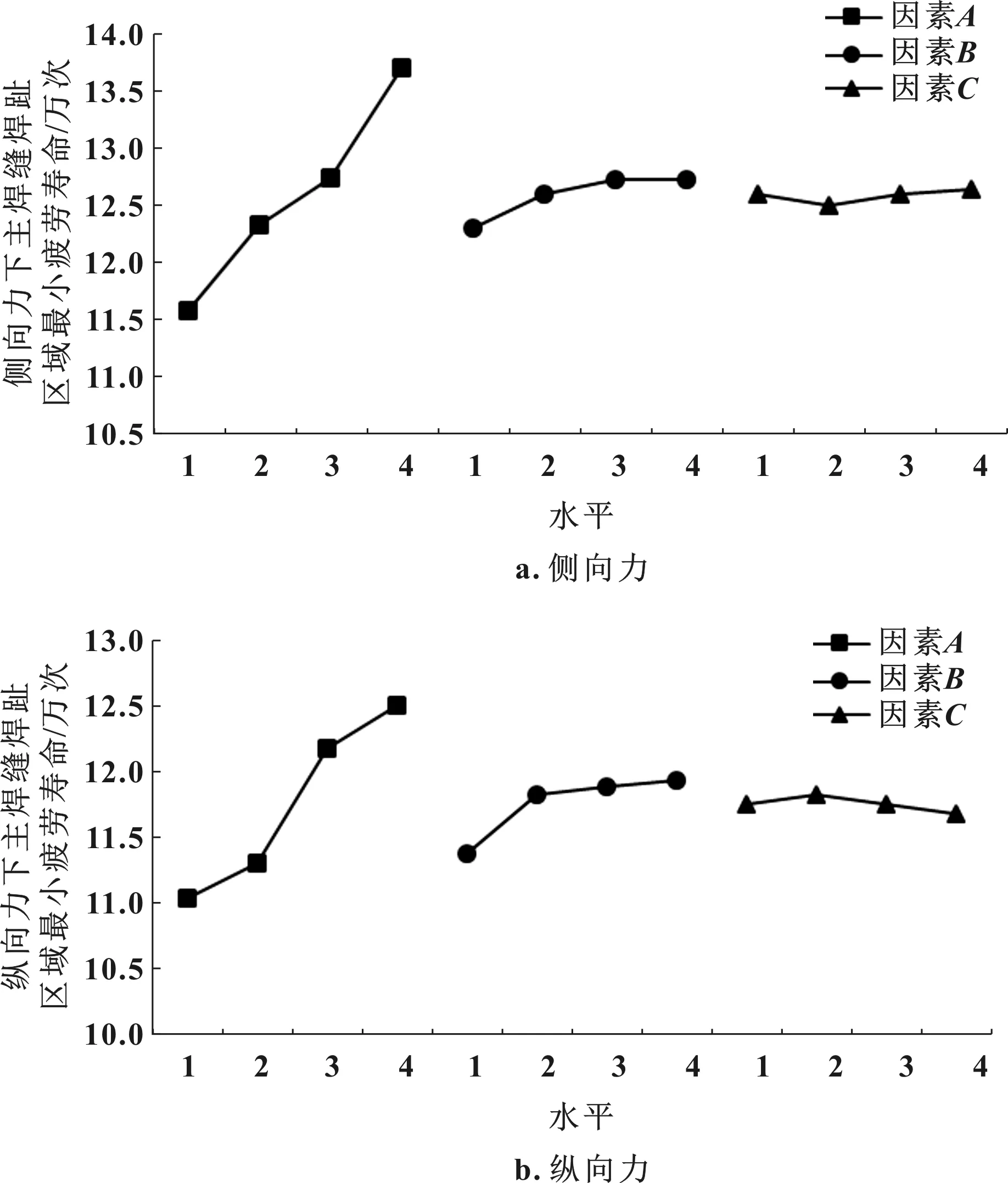
图7 各因素对侧向力和纵向力下主焊缝焊趾区域最小疲劳寿命的影响

对两个试验指标分别进行计算发现，对于侧向力及纵向力下主焊缝焊趾区域最小疲劳寿命，影响因素的主次顺序均为A、B、C，即，纵臂板厚、加强支架及所处位置、弹簧托盘在横梁上的搭接型面末端与主焊缝距离。

由图7可知，以侧向力下主焊缝焊趾区域最小疲劳寿命为优化指标时，最优的结构参数组合为A4B3(B4)C4；以纵向力下主焊缝焊趾区域最小疲劳寿命为优化指标时，最优的结构参数组合为A4B2(B4)C2。

上述两个最优结构参数组合并不完全相同，需对试验的相关数据进行进一步的方差分析，以确定试验结果波动的主要原因，方差分析结果见表4。

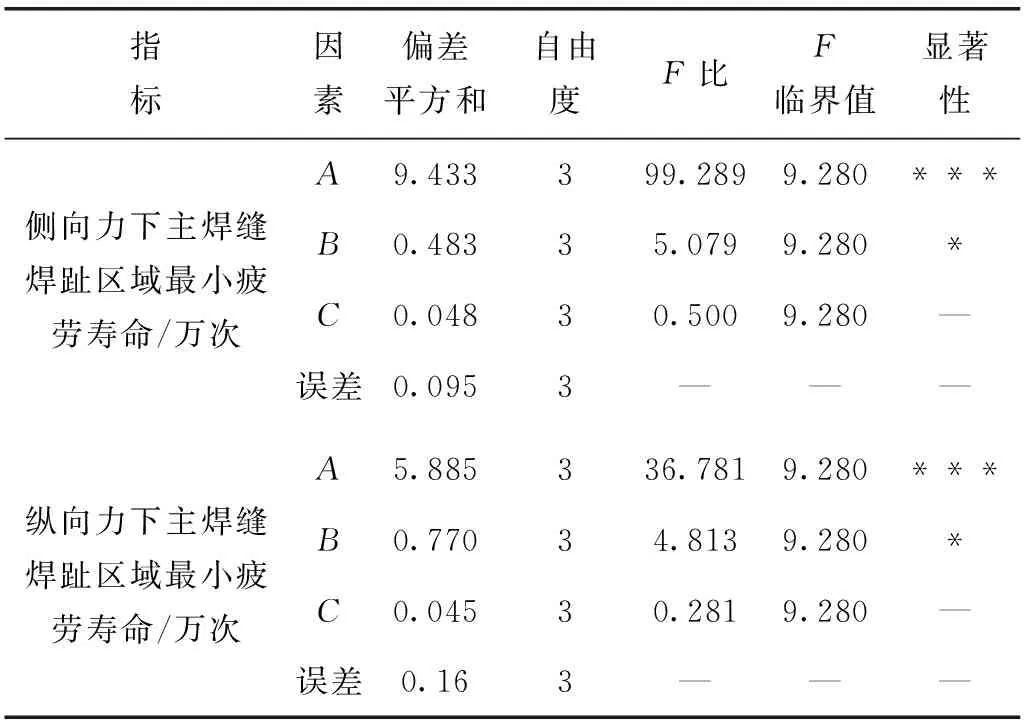
表4 方差分析结果

由表4的各因素对试验指标影响的显著性可以得出，因素A和因素B对侧向力、纵向力下主焊缝焊趾区域最小疲劳寿命的影响都具有显著性，但综合两者的偏差平方和可知，因素A的影响大于因素B。选取A4和B4水平可以同时保证纵向力和侧向力下主焊缝焊趾区域最小疲劳寿命有较好表现，因素C对两个优化指标都不具有显著性，综合考虑制造阶段的焊接工艺性，选取弹簧托盘在横梁搭接型面与主焊缝距离为15 mm，可使两条焊缝热影响重叠区域相对较少，最终得出最优的结构参数组合为A4B4C4。

4 优化方案验证

在基准结构组合(纵臂厚度为3.2 mm、无加强支架、弹簧托盘在横梁搭接型面与主焊缝距离为0)的基础上对上述正交试验所得最优结构参数组合(纵臂厚度为4.0 mm、加强支架位于主焊缝下部、弹簧托盘在横梁搭接型面与主焊缝距离为15 mm)进行样件试制，并在纵向力和侧向力单工况台架下对比优化前后的主焊缝焊趾区域最小疲劳寿命，具体见表5。由表可以看出，优化后结构在纵向力下的疲劳寿命由10.8万次提高至13.2万次，增幅为22.2%；侧向力下的疲劳寿命由12.3万次提高至14.9万次，增幅为21.1%。由此可见采用优化后的结构能显著提高该区域在纵向力及侧向力台架下的疲劳寿命。

表5 优化前后的主焊缝焊趾区域最小疲劳寿命

图8和图9分别为优化前后扭梁主焊缝焊趾区域在纵向力及侧向力单工况台架下的失效图片。由图可知，扭梁焊缝最先失效位置均在与弹簧盘的交界附近位置的主焊缝上，这与有限元模拟结果吻合，也说明了上述正交试验所得到的最优结构因素组合可靠性较高，具有一定的指导意义。

图8 优化前扭梁主焊缝焊趾区域在纵向力和侧向力单工况台架下的失效图片

图9 优化后扭梁主焊缝焊趾区域在纵向力和侧向力单工况台架下的失效图片

5 结论

(1)以纵向力下主焊缝焊趾区域最小疲劳寿命为指标，得出最优结构因素组合为：纵臂厚度4.0 mm，加强支架位于主焊缝中部或下部，弹簧托盘在横梁上的搭接型面与主焊缝距离15 mm;各因素对纵向力下主焊缝焊趾区域最小疲劳寿命的影响程度由大到小为：纵臂板厚、加强支架及所处位置、弹簧托盘在横梁上的搭接型面与主焊缝距离。以侧向力下主焊缝焊趾区域最小疲劳寿命为指标，得出最优结构因素组合为：纵臂厚度4.0 mm，加强支架位于主焊缝上部或下部，弹簧托盘在横梁上的搭接型面与主焊缝距离5 mm;各因素对侧向力下主焊缝焊趾区域最小疲劳寿命的影响程度由大到小为：纵臂板厚、加强支架及所处位置、弹簧托盘在横梁上的搭接型面末端与主焊缝距离。

(2)综合考虑各因素对两个指标的影响，并结合焊接工艺性，最终确定最优结构参数组合为纵臂厚度4.0 mm，加强支架位于主焊缝下部，弹簧托盘在横梁上的搭接型面与主焊缝距离为15 mm。

(3)根据最优结构参数组合进行改善样件试制并进行纵向力和侧向力的单工况台架耐久。结果表明，优化后结构在纵向力下的疲劳寿命由10.8万次提高至13.2万次，增幅为22.2%；侧向力下的疲劳寿命由12.3万次提高至14.9万次，增幅为21.1%，采用优化后的结构能显著提高该区域在纵向力及侧向力台架下的疲劳寿命。台架试验的扭梁焊缝失效位置均在横梁与弹簧盘的交界附近位置的主焊缝上，这与数值模拟结果吻合，说明了上述正交试验所得到的最优结构因素组合可靠性较高，具有一定的指导意义。