灵活运用构造函数法，提升证明不等式的效率

程学梅

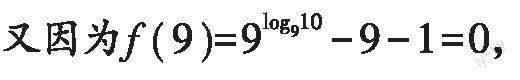
通過分析近几年全国各省市的高考试题，不难看出证明不等式问题是数学高考中的必考内容，且多数以压轴题的形式出现.证明不等式的方法很多，其中构造函数法比较常用，且十分奏效.由于各道题目中的条件和不等式均不同，所以构造函数的方法也有所不同，那么，如何构造出合适的函数呢？下面结合实例进行探讨.

一、通过作差构造函数

有些不等式两侧的式子均为多项式，此时可以将不等式两侧的式子作差，即使不等式的一侧为0，便可将另一侧的式子构造成函数.再根据函数单调性的定义或导数与函数单调性之间的关系判断出函数的单调性，即可根据函数的单调性求得函数的最值，证明函数的最值恒大于或小于0，就能证明不等式成立.

例1.证明：当0

证明：令[h（x）=x-x2-sinx]，

则[h（x）=1-2x-cosx，]

可得[h（0）=0，h（0）=0]，

且[h（x）=-2+sinx<0，]

所以[h（x）]在（0，1）上单调递减.

当0

所以[h（x）=x-x2-sinx]在（0，1）上单调递减.

当[0

所以当[0

令[g（x）=x-sinx，g（0）=0， g（x）=1-cosx≥0]，

所以[g（x）]在（0，1）上单调递增.

当[0g（0）=0，]所以[sinx

所以当[0

要证明该不等式，需分两步：首先证明[x-x20即可.

二、根据同构式的特点构造函数

有时将不等式或等式左右两侧的式子进行适当的变形，如移项、通分、去分母、取对数等，可使不等式或等式左右两边的式子化为结构相同、形式相似的式子，即同构式.再由其形式特征构造出新函数，讨论函数的单调性、极值、最值，即可解题.

例2.已知[9m] = 10，[a=10m-11]，[b=8m-9]，则（     ）.

A. a＞0＞b B. a＞b＞0

C. b＞a＞0 D. b＞0＞a

解：因为[9m]=10，所以m=log910，

而[a=10m-10-1]，[b=8m-8-1]，

设[f（x）=xm-x-1（x>1）]，

则[f（10）=a， f（8）=b]，

所以[f（x）=mxm-1-1]，

故[f（x）=xm-x-1]在（1，+∞）上单调递增，

故[f（10）>f（8）].

所以[a>0>b]，

故选A．

将a、b进行配凑，得到[a=10m-10-1]，[b=8m-8-1]，即可使其为同构式，便能构造出与其结构一致的函数[f（x）=xm-x-1].在解题时，需仔细观察不等式或等式，将其进行适当的变形，才能构造出同构式，进而构造相应的函数模型.

三、通过换元构造函数

有些不等式或等式较为复杂，此时可采用换元法，将其中的某个式子或者一部分用一个新元替换，从而简化代数式，再构造出函数模型，便可利用函数的性质、图象快速证明不等式.

例3.已知函数f（x）= -k有2个不同的零点x1，x2，求证：x1x2＞e2.

由[f（x1）=f（x2）=0，]

可得[lnx1-kx1=0，lnx2-kx2=0，]

将两式相加减，得ln x1＋ln x2 = k（x1＋x2），

ln x1 -ln x2 = k（x1-x2）．

要证x1x2＞e2，即证ln x1x2＞2，

只需证ln x1＋ln x2＞2，

故函数[h（t）]在（1，＋∞）上单调递增，

所以[x1x2>e2].

对于二元不等式问题，往往需先寻找并建立两个变量之间联系，如和差关系、倍数关系；然后令m（x1，x2） = t，通过换元，构造出关于新元t的式子；再将其视为函数式，利用函数的单调性来证明不等式.

四、通过分离参数构造函数

若遇到含参不等式，则通常要将不等式中的参数、变量分离，使其分别置于不等式的两侧，再将含有变量的式子构造成函数，即可通过分离参数，构造出函数模型.在分离参数时，要注意参数的符号，根据不等式的性质将参数分离出来，最后研究函数的最值或极值，便可证明不等式．

证明：因为[f（x）=（2-a）（x-1）-2lnx]，

所以由[f（x）>0]得[（2-a）（x-1）-2lnx>0]，

即[a≥2-4ln2].

在分离参数后，构造出函数，即可将问题转化为证明[f（x）≥g（a）]或[f（x）≤g（a）]，求得函数的最值，证明[f（x）min≥g（a）]或[f（x）max≤g（a）]即可.对于含有指数、对数式的不等式问题，通常要先求出函数的导数；接着以导数知识为工具来研究该函数的单调性；最后求得函数的极值、最值，从而达到证明不等式的目的．

总之，无论运用哪种方法构造函数，都需要仔细研究不等式的结构特征，对其进行合理的变形，如换元、移项、分离参数、构造同构式，以构造出合适的函数模型；通过研究函数的单调性、最值、极值，从而顺利证明不等式.同学们需多练习、多思考、多积累、多总结，才能在考试时信手拈来，构造出合适的函数模型，顺利破解难题.