涡轴发动机时延鲁棒串级PI 控制器设计
陈义峰,郭迎清,毛皓天
(西北工业大学 动力与能源学院,西安 710072)
当前,涡轴发动机在军用与民用领域广泛的应用于直升机、发电机和地面车辆的辅助动力装置等。直升机是一个高度集成的系统,其升力通过总矩杆角度进行控制,因此,当前涡轴发动机的控制方式为功率涡轮定转速控制。涡轴发动机主要由燃气发生器和功率涡轮两部件组成,而功率涡轮与主旋翼连接并通过燃气发生器产生的燃气进行驱动。由于旋翼系统是一个大惯性系统,当前涡轴发动机多采用串级控制系统结构,以内环控制器保证燃气发生器的快速响应而以外环控制器保证转子系统的转速恒定[1-3]。
分布式控制系统具有系统重量轻、可靠性高、模块化、低生命周期成本及利于新控制技术(如主动控制技术等)的整合等优点。随着人们对发动机性能需求的不断提高,这些优点引起了人们的持续关注,分布式控制系统被认为是未来发动机控制系统的发展方向之一[4-6]。分布式控制系统中,传统的传感器/执行机构将被相应的智能传感器/执行机构所取代,这些节点通过通信网络进行相互连接。控制系统中的所有信号都在数据总线上进行传输[5]。
对于涡轴发动机串级控制系统,当其所有节点通过总线实现通信时,该系统被称为网络串级控制系 统(networked cascade control system,NCCS)[2]。由于总线带宽约束或节点瞬时失效等原因,数据传输过程中不可避免的会存在时延问题,而这些时延会导致系统的性能降低甚至导致系统失稳[3,7]。因此,为了保证系统的控制性能,控制系统必须对时延具有鲁棒性。
针对NCCS,Huang 等[7]开展的相关研究中,提出了4 种NCCS 结构并对其时延进行了分析,针对系统中的固定时延,文献[8]设计了串级比例-积分-微分(proportional-integral-derivative,PID)控制器,文献[9]针对一个控制周期内的短时延设计了串级H∞控制器,文献[10-11]则针对固定时延提出了内模控制(internal model control,IMC)方法和二自由度方法等鲁棒串级PID 控制器设计方法。对于涡轴发动机分布式控制系统,Belapurkar 和Yedavalli[2]提出了2 种串级控制系统结构,并采用LQR方法设计了长时延下的串级状态反馈控制器;Chen等[12]采用Lyapunov- Krasovskii 方法给出了静态串级控制器设计方法,并利用区域极点配置方法来保证系统的动态性能;Liu 等[3,13]针对涡轴发动机分布式控制系统中存在的时延与随机丢包等问题,提出一种新的分析时延系统稳定性及求解最大允许时延的方法,以及利用Lyapunov 定理给出了存在随机丢包的系统控制器设计方法。文献[2,12-13]针对涡轴发动机分布式控制系统的研究都是直接从静态控制器的角度进行控制器设计。
在当前的涡轴发动机控制中,PID 控制仍是一种非常重要的控制方法。本文针对涡轴发动机分布式控制系统中存在的时延设计了鲁棒串级PI 控制器。首先,分析了涡轴发动机分布式串级控制系统的结构及时延组成,利用IMC 方法处理串级控制系统内外环同时存在的时延,并确定了此串级控制系统的控制器为串级PI 控制器结构;然后,利用频域回路成形的方法,确定了保证系统具有期望的动态性能约束,并将控制器设计问题转化为具有线性矩阵不等式(linear matrix inequality,LMI)约束的广义特征值求解问题;接着,为了保证系统稳定,利用梯度近似的方法将劳斯-赫尔维茨判据转化为LMI 形式的约束,将所有的约束进行综合并求解优化问题获得期望的鲁棒串级PI 控制器的内外环参数;最后,利用基于TrueTime 的涡轴发动机分布式仿真平台对控制器进行了数字仿真验证。
1 鲁棒串级PI 控制器设计
对于涡轴发动机分布式控制系统的时延鲁棒串级PI 控制器设计方法包括三部分:IMC-PI 控制器的设计,LMI 形式的频域回路成形约束条件及LMI 形式的稳定性约束条件获取。
1.1 串级IMC-PI 控制器的设计
当前的涡轴发动机控制系统,针对转子系统的大惯性特性,为了保证转子转速恒定,同时,燃气发生器具有较快的响应速度,采用的串级控制系统结构如图1 所示[2]。其内环为燃气发生器的转速Ng控制系统,而外环为转子系统的转速Np控制系统,系统的输入为参考转速r,控制量为燃油流量Wf,燃气发生器输出轴力矩Qs用于驱动转子系统,而旋翼系统的功率需求LDL 是涡轴发动机控制系统的扰动量。
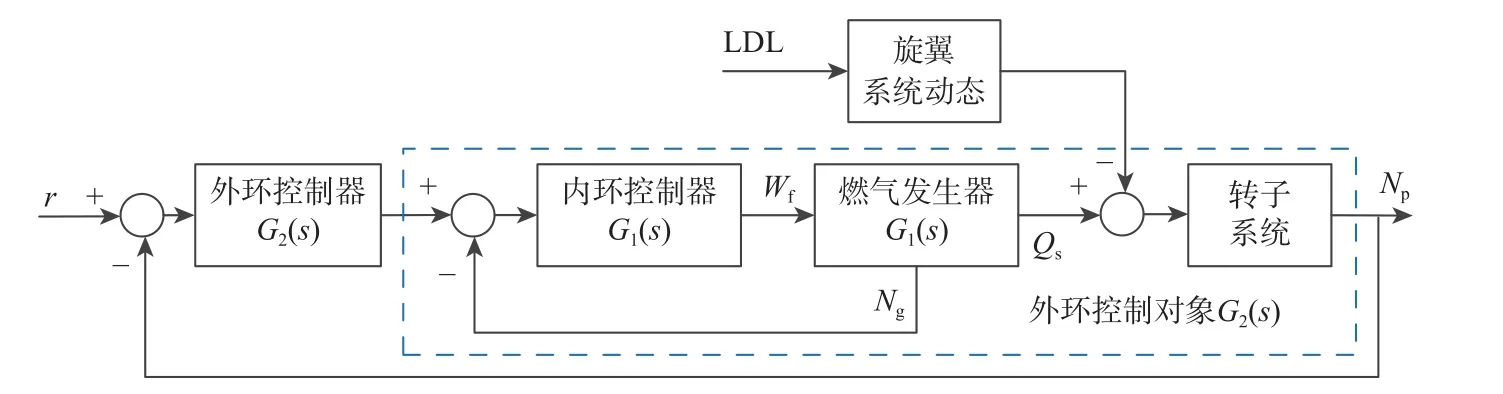
图1 涡轴发动机串级控制系统原理[2]Fig.1 Block of cascade control system of turboshaft engine[2]
根据内外环传感器、内外环控制器、执行机构和控制对象之间的通信方式,NCCS 被分为4 类[7]。对于涡轴发动机分布式控制系统,当系统的所有控制算法仍在全权限数字电子控制器(full authority digital electronic controller,FADEC)中计算时,涡轴发动机分布式控制系统属于第三类NCCS[14],即传感器与控制器之间、控制器与执行机构之间都通过网络连接,而内外环控制器是同一个节点,其结构如图2 所示。
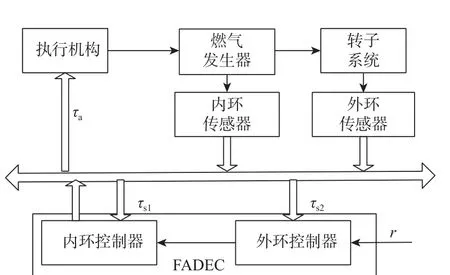
图2 涡轴发动机分布式控制系统第ⅢNCCS 结构示意图Fig.2 Type Ⅲ NCCS configuration of distributed control system of turboshaft engine
涡轴发动机分布式控制系统内的时延包括3 个:内环传感器与内环控制器之间的时延 τs1,外环传感器与外环控制器之间的时延 τs2和控制器与执行机构之间的时延 τa。
当采用传统传递函数方法直接设计串级PI 控制器时,内环时延会对外环控制对象产生复杂的影响从而导致外环控制器设计复杂化。采用IMC 方法可以明确串级控制系统内外环时延的关系[10]:内环时延为所有内环节点之间时延之和,而外环时延为内环总时延与外环所有节点之间时延之和。因此,对于本节涡轴发动机NCCS,可以利用IMC方法从内环到外环依次设计PI 控制器,且此时系统的内环时延为 τ1=τs1+τa,而外环时延为τ2=τ1+τs2。
以单环控制系统为例说明采用IMC 方法设计控制器的步骤,对于串级控制系统则从内环到外环逐层进行设计[10]。对于一个单位负反馈的闭环IMC 控制系统,其结构如图3 所示,G(s) 为控制对象的传递函数,根据IMC 控制器设计方法[15-16],控制对象的模型 G ˆ(s) 为

图3 IMC 控制系统结构示意图Fig.3 IMC control system

式中:q(s)=G-M1(s)f(s)为 内模控制器,f(s)=1/(λs+1)n为IMC 滤波器,其阶数 n在选择时必须保证控制器具有适当的阶数,而常数 λ为待设计参数。
针对某型民用涡轴发动机,本文利用GasTurb软件和MATLAB 环境构建了该型涡轴发动机的部件级模型及仿真平台[17]。通过系统辨识的方法可以得到该型涡轴发动机在地面静止状态下,燃气发生器转速Ng和转子系统转速Np均为100%状态时燃气发生器增量模型 G1(s) 为带有正零点的一阶传递函数,并且将内环时延作为时滞环节,其表达式为
式中:s为 传递函数自变量;K1、β11和 α11为模型的常数系数;e 为自然常数。模型的输入为燃油流量增量ΔWf,kg/s;输出为燃气发生器的转速增量ΔNg,r/min。
针对此控制对象利用IMC 方法设计控制器,用一阶Pade 近似时滞环节,此时可得
式中:φ 为 2λ2+0.5τ2-β21的 缩写形式;λ2为外环控制器待设计参数,所以外环控制器为带有双二阶滤波器的PI 控制器。
1.2 鲁棒PI 参数约束
在确定PI 控制器结构后就需要对控制器的参数进行求解。对于一个单位负反馈PI 控制系统,假设其控制器为C (s) ,而系统的控制对象仍为G (s)。PI 控制器设计目标是求解合适的控制器参数,使得闭环系统具有期望的性能及足够的鲁棒性。而系统的性能与开环系统频域幅相曲线的形状具有高度相关性。因此,利用频域回路成形的方法可知期望的控制器需要同时满足以下的约束条件[18-20]:
1)为了保证系统具有期望的穿越频率及相位裕度,开环传递函数需满足:
式中:ωc为期望的穿越频率,rad/s;ϕm为期望的相位裕度,rad。

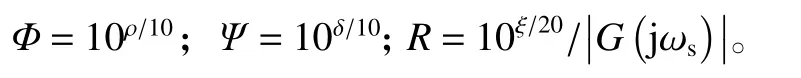
对于带约束式(13)~式(16)的广义特征值问题,约束式(13)~式(15)都是LMI 约束,但约束式(16)是非线性约束。约束式(16)的可行域为半径为R 的圆以外的区域,但该区域为非凸区域,无法利用LMI 工具箱求解。为了对优化问题进行求解,利用圆的切线将可行域分成4 个凸可行域进行求解,如图4 所示,4 个凸可行域可表示为

图4 由4 条切线构成的凸可行域Fig.4 Feasible convex region divided by four tangents
1.3 涡轴发动机串级PI 控制器的稳定性约束
1.2 节给出的PI 控制器参数整定约束条件式(8)~式(11)主要是保证系统具有期望的性能,但系统的稳定性还需要额外的条件进行约束。可通过劳斯-赫尔维茨判据来对控制器参数进行约束,该方法在文献[18]中已给出。
对于涡轴发动机分布式控制系统串级PI 控制器,首先,确定内环PI 控制器参数的约束条件,然后,再确定外环PI 控制器参数的约束条件。



同时定义2 个梯度矩阵:
至此,关于时延鲁棒串级PI 控制器设计的所有LMI 形式约束已经得到,然后利用LMI 工具箱YALMIP 对其进行求解[22],便可以得到期望的涡轴发动机分布式控制系统内外环PI 控制器的相关参数,最 后 通 过 式(5)和 式(7)分 别 得 到 内 外 环 的IMC 滤波器参数 λ1和 λ2,从而得到串级控制系统内环一阶滤波器和外环双二阶滤波器的相关参数。
2 基于TrueTime 的非线性仿真
本节主要通过基于TrueTime 工具箱搭建的某型涡轴发动机分布式控制系统非线性仿真平台来验证所设计的时延鲁棒串级PI 控制器的有效性及性能。
对于某型涡轴发动机,通过系统辨识的方法可以得到燃气发生器加时延的模型式(3)的表达式为


涡轴发动机整机的期望带宽在0.1~3.5 rad/s,因此,约束式(8)~式(11)中的参数分别取 ωc=3 rad/s、ϕm=85°,ξ=10 dB、ωs=0.1 rad/s,ρ=-10 dB、ωt=50 rad/s,δ=-10 dB、ωr=50 rad/s。假设外环传感器到控制器的时延 τs2=0.02 s,则外环控制系统的时延为 τ2=τ1+τs2=0.04 s,即模型的时滞环节为 e-0.04s。最后利用1.2 节与1.3 节联合的控制器设计方法可以得到外环PI 控制器的参数X2=[0.3093 3.2935]T,外环IMC 滤波器参数λ2=0.333 3。在得到内外环的控制器后,内外环的开环幅相曲线如图5 和图6 所示。通过幅相曲线可以看出,带有控制器的开环系统具有足够大的低频增益(大于30 dB)和足够小的高频增益(小于-14 dB),内环穿越频率为期望频率(9 rad/s),外环穿越频率为1 rad/s。

图5 内环开环系统的Bode 图Fig.5 Bode plot of inner open loop
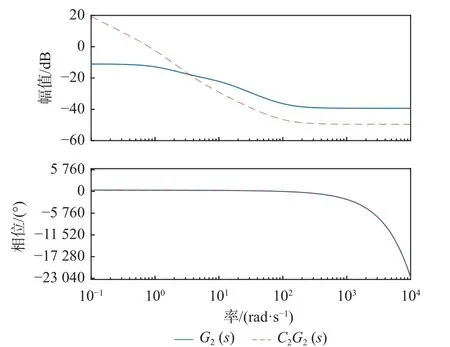
图6 外环开环系统的Bode 图Fig.6 Bode plot of outer open loop
在MATLAB 环境中利用Simulink/TrueTime 工具箱[24]搭建的涡轴发动机分布式控制系统非线性仿真平台采用部分分布式结构[14],其原理如图7所示。
在图7 中,采用网络模块来仿真总线特性;智能传感器、数据集中器、智能执行机构及FADEC节点都采用计算模块来仿真,最上部为串级PI 控制器结构。网络模块可以仿真9 种总线通信协议,此平台选择CAN 总线通信协议,并通过参考消息的方式实现TTCAN 总线通信,带宽选择最高1 Mbps,由于不考虑丢包问题,丢包率设置为0。仿真过程中,节点的固定时延通过在节点初始化程序中用ttSetNetworkParameter 函数进行设置,随机时延通过Simulink 中的可变传输时延模块加入智能执行机构中。
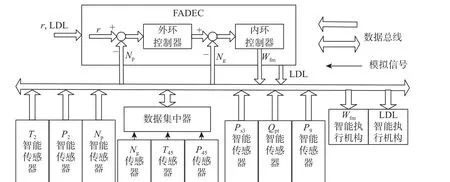
图7 基于TrueTime 的涡轴发动机分布式控制系统仿真平台Fig.7 Simulation platform of TrueTime based distributed control system of turboshaft engine
在仿真中,对比鲁棒串级PI 控制器与利用PID Tuner 工具箱设计得到的传统串级PI 控制器的性能。利用该工具箱设计串级PI 控制器时内外环的幅值与相位裕度保持一致,得到其内环参数为KP1=3.16×10-5,KI1=7.9×10-5,外环控制器参数为KP2=4.817,KI2=10.44,涡轴发动机的控制周期为0.02 s,控制器的离散化采用Tustin 方法。首先,仿真微小时延(仿真系统中信号传输时延为0.001 5 s,即时延在一个控制周期内);然后,对控制器设计点的时延(总时延为0.04 s,即2 个控制周期内)进行仿真;最后,为了比较2 个控制器对于时延的鲁棒性,将仿真总时延增加到3 个控制周期,即τs1=τs2=τa=0.02s,总矩杆角度由100%下降到95%,分别在2 个串级控制器作用下,系统的参数相对变化量如图8 所示。
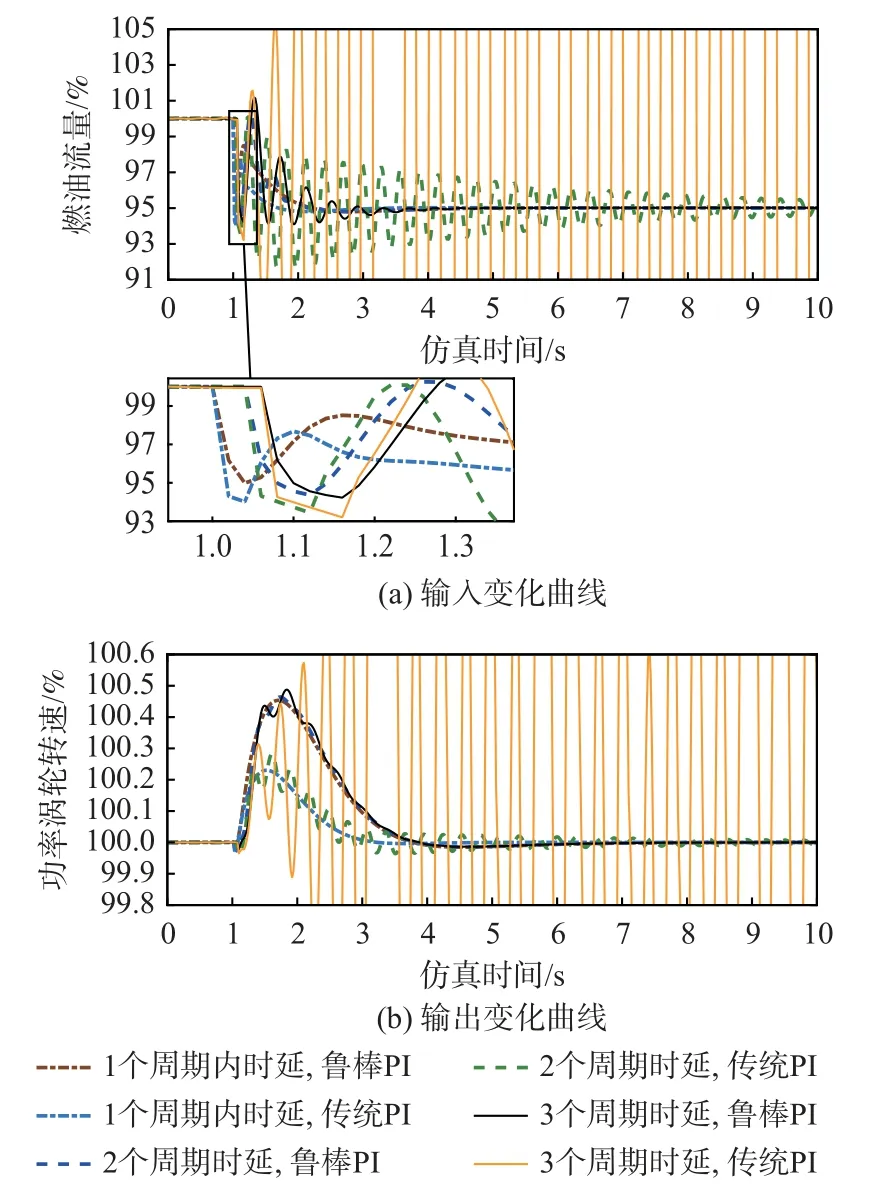
图8 外环穿越频率为3 rad/s,不同时延时2 个控制器作用下系统的性能比较Fig.8 Comparison of control performance of two controllers with different time delays when crossing freqency of outer loop is 3 rad/s
从图8 可以看出,当时延分别在1 个控制周期内和2 个控制周期内时,2 个串级PI 控制器都能保持系统的稳定,且功率涡轮的转速超调小于0.5%,调节时间小于5 s(涡轴发动机小扰动下的性能指标为[25]:Np超调不超过5%~7%,稳态精度为0.2%左右,调节时间为8~10 s),当时延增加到3 个控制周期时,传统的串级PI 控制器无法保证系统稳定,而鲁棒串级PI 控制器仍能保证系统稳定。因此,鲁棒串级PI 控制器对时延具有更强的鲁棒性,能够容忍更大的时延,且通过仿真可知其保证系统稳定的时延边界为0.097 s,传统串级PI 控制器的时延边界为0.057 s,即控制系统稳定时延容忍边界由原来不足3 个控制周期(0.06 s)扩大到了接近5 个控制周期(0.1 s)。从燃油流量可以看出时延条件下鲁棒串级PI 控制器下最大燃油流量变化率为0.259 6 kg/s2,而传统串级PI 控制器下最大燃油流量变化率为0.386 5 kg/s2,说明鲁棒串级PI 控制器对执行机构的快速性要求降低。

从图9 可以看出,分别在0.001 5 s(1 个周期内)和0.04 s(2 个控制周期)时延下,2 个控制器都能满足控制需求,而当时延增加到4 个控制周期时,传统控制器便不能保证系统稳定而在鲁棒串级PI 控制器作用下系统仍能保持稳定且系统性能满足要求,且传统控制器的时延边界只有0.077 s(不足4 个周期),小于鲁棒串级PI 控制器的时延边界。
同时,从图8 与图9 对应的仿真结果可以得到,2 个传统串级PI 控制器的时延边界存在差异,主要是由其外环期望穿越频率的差异导致的,外环期望穿越频率越大,系统的响应速度越快而系统的鲁棒性就越差。所以,鲁棒串级PI 控制器相比于传统串级PI 控制器,能够保证涡轴发动机在时延条件下的性能与鲁棒性有一个更好的协调性且实现该控制所需代价更小。
图8 与图9 对应的计算与仿真针对的都是固定时延,但该时延鲁棒串级PI 控制器对于上限不超过计算设定时延(0.04 s)的随机时延也是有效的。在固定时延与随机时延下,系统的响应曲线及随机时延的大小如图10 所示。从图10 可以看出,在随机时延下,功率涡轮转速Np的超调不超过0.5%,调节时间小于5 s。因此,随机时延不超过上限时鲁棒串级PI 控制器仍是有效的。

图10 在固定时延与随机时延下系统性能对比Fig.10 Performance comparison with constant and random time delays
3 结 论
对涡轴发动机分布式控制系统中存在时延下的鲁棒串级PI 控制器设计方法进行了研究。得到以下结论:
1)对于内外环同时存在时延的涡轴发动机分布式控制系统,IMC 控制器设计方法是一种有效的设计PI 控制器的方法。
2)在鲁棒串级PI 控制器作用下,系统能够满足控制需求且能够容忍的时延边界扩大为0.097 s(将近5 个控制周期)大于传统串级PI 控制器。说明通过频域回路成形方法与LMI 方法相结合,可以为存在时延的涡轴发动机分布式控制系统设计出鲁棒性更好的控制器以应对时延对涡轴发动机分布式控制系统性能的影响,并实现鲁棒性与动态性能更好的协调。
但在控制器设计过程中,约束条件的转换采用了一些保守性方法,如何解决求解方法的保守性是未来值得研究的问题。

