基于MSST 及HOG 特征提取的雷达辐射源信号识别

全大英，唐泽雨，陈赟，楼维中，汪晓锋，章东平

(1.中国计量大学 信息工程学院 浙江省电磁波信息技术与计量检测重点实验室，杭州 310018；2.中国电子科技集团有限公司第五十二研究所，杭州 310000)

电子侦察在电子对抗领域发挥着至关重要的作用[1]，而低截获概率(low probability of intercept,LPI)雷达信号识别是电子侦察的关键因素[2-3]，有效识别LPI 雷达信号可以帮助我方掌握战场主动权，进而影响进一步的作战决策[4]。传统雷达信号识别主要基于脉冲宽度、脉冲幅度、载波频率、到达时间和到达角等常规参数特征。基于信号间参数的识别技术在信号流密度低、信号形式简单、辐射源数量少、电磁环境简单的情况下可以达到较好的效果，然而随着雷达技术的进步，战场电磁环境日益复杂，LPI 雷达具有低截获、高探测、大时宽和强干扰等特点，传统方法已不能满足识别需求。

由于新型雷达信号具有丰富的脉内信息，可通过分析信号脉内特征参数来提升识别的准确性[5]。近年来，国内外众多学者通过分析雷达信号时域、频域和时频域特征对雷达信号识别问题展开了多项研究。文献[6]根据雷达信号频谱特点，利用复杂度计算思想从几何形状上描述信号特征，提出基于频谱复杂度的雷达信号调制方式识别方法，该方法在信噪比为6 dB 时整体识别率可以达到90%以上，但随着频率分辨率降低，无法区分非线性调频信号和线性调频信号频谱的几何图形，导致识别结果不理想。文献[7]通过分数阶傅里叶变换对信号进行Chirp 基分解，按照Chirp 基载频与调频率的不同组合对信号划分类别，并设置对应的分类特征参数，计算信号的伪Wigner-Ville 时频分布，并提取Zernike矩特征，将上述特征参数组成信号特征矢量，使用残差神经网络分类器实现雷达信号识别，当信噪比为-2 dB 时，该算法识别准确率平均可达到93%，但对BPSK 信号识别率较低。文献[8]在Choi-Williams时频分布(Choi-Williams distribution, CWD)的基础上，对图像进行伪Zernike 矩和中心矩特征提取，从而实现对信号的分类识别，但在低信噪比情况下，该算法识别率较低。文献[7-8]基于Wigner-Ville分布(Wigner-Viller distribution, WVD)和CWD 时频变换提取信号的图像特征，但由于WVD 和CWD时频分辨率有限，对细节的描述不够，不能体现不同信号之间的细微差别，从而影响识别的准确率。针对文献[7-8]中时频分辨率低的问题，文献[9]提出了基于短时傅里叶变换(short-time Fourier transform,STFT)的同步压缩（synchrosqueezing transform, SST）方法，即在STFT 的基础上，将信号频率进行压缩，以达到“挤压”的目的[10]。相比于WVD 和CWD 时频变换，经同步压缩之后的时频分布图分辨率更高，有利于雷达信号的准确识别。然而，同步压缩在处理复杂时变信号时，时频聚集性会大大降低，导致时频模糊，随着信号非平稳性的增强，瞬时频率估计偏差越来越大。

为了解决WVD 和CWD 时频分辨率不足及时变信号同步压缩后时频模糊的问题，本文首先采用多重同步压缩（multi-synchrosqueezing transform,MSST）的方法对信号进行时频变换，即在原同步压缩的基础上进行多次迭代计算，实现频率方向上的时频系数重排，在保证时频聚集性的同时缓解了同步压缩时频特征模糊和能量发散问题。然后，通过图像预处理算法，进一步抑制噪声干扰，并减少特征提取过程中的运算量。预处理过程中，采用全阈二值法选择灰度图中的最佳阈值，有利于方向梯度直方图(histogram of oriented gradient, HOG)特征算法提取时频图像中信号轮廓的方向梯度值作为特征参数。同时，为了去除高维HOG 特征中的冗余特征量，采用主成分分析法(principal component analysis,PCA)进行降维。最后，利用支持向量机(support vector machines, SVM)实现雷达信号的分类识别。

1 MSST 时频变换与HOG 特征提取

由于雷达信号种类众多，难以全面遍历研究，选取包括 CW、LFM、NLFM、2FSK、BPSK、QPSK、LFM/FSK、LFM/BPSK 及FSK/BPSK 在内的9 种典型的雷达信号作为研究对象。为了实现在低信噪比下对这9 个雷达信号的识别，提出了一种基于MSST 时频变换的HOG 特征提取的新方法。

1.1 MSST 时频变换

MSST 是一种新的时频分析方法[11-12]，通过在STFT 获得的时频谱基础上进行多重同步压缩，可有效提高时频分布图的分辨率，并利用迭代算子优化算法流程，减轻计算负担。同时，MSST 作为一种线性时频工具，不存在交叉项的干扰。对于给定的雷达信号 s(u)，其STFT 可定义为[13]

式中：g (u)为窗函数；w 为频率。

信号 s(u)可进一步展开为

式中：δ(t)为脉冲函数。通过执行同步压缩可从频率方向上对STFT 时频分布图进行压缩。

然而，SST 在处理复杂时变信号时，信号的瞬时频率估计偏差增大，时频聚集性大大降低，导致时频模糊。而MSST 通过迭代计算，实现频率方向时频系数的多次重排，可有效处理强调制信号和强时变信号，同时，在一定程度上能缓解同步压缩时频特征模糊和能量发散等问题。MSST 的具体迭代过程如下：

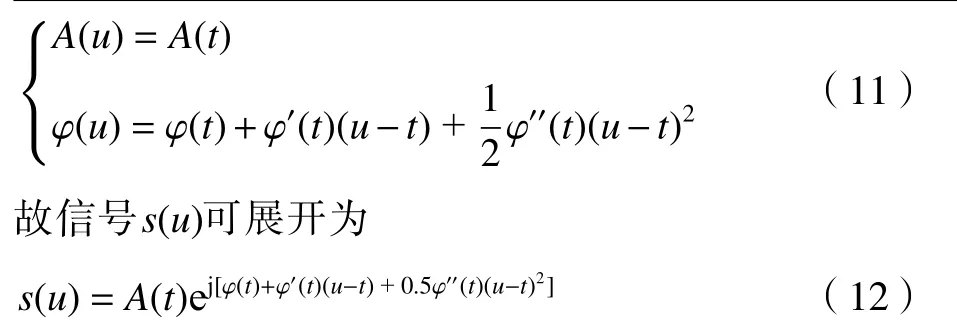
若将窗函数指定成高斯窗 g(u)=e-0.5u2，则上述信号的STFT 表达式为

将式（13）代入式（7）中，可得瞬时频率估计取实部后为

式（16）表明了第二次同步压缩的瞬时频率wˆ(t, wˆ(t,w))比 只压缩一次的瞬时频率 wˆ(t,w)更加接近信号的真实瞬时频率，即当 N=2 时 比 N=1能得到能量更加集中的时频谱。

同理，可得 N=3时有，

由式（20）可以看出，原始时频平面上的轨迹点从 (t,w)变 换为 (t, wˆ[N](t,w))，信号瞬时频率逐渐向真实瞬时频率靠近，信号瞬时频率得到有效压缩。

针对上述9 种典型雷达信号，图1 给出了信噪比为10 dB 时的MSST 时频分布图像。可以看出，9 种雷达信号的时频图表现出了明显差异。

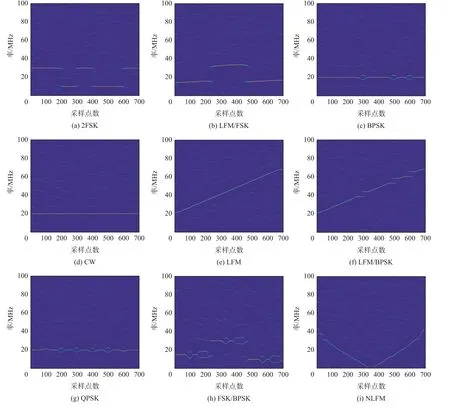
图1 九种雷达信号的MSST 时频图Fig.1 MSST time-frequency images of 9 kinds of radar signals

由于战场电磁环境复杂，各种设备的存在会对接收机产生噪声干扰，雷达时域信号时频化虽能有效降低噪声干扰，但时频图像中仍存在大量干扰信息，在特征提取前需先对时频图进行预处理。图2给出了该预处理流程及时频图变换的示意图。

图2 图像预处理流程Fig.2 Flow of image preprocessing

时频图预处理过程可具体描述如下：

1）将656×875 像素的原始图像剪裁成535×679像素的图像，去掉图像中的无效信息，可有效降低运算量，提高运行速度。

2）对剪裁后的图像进行灰度化处理得到灰度图。

3）通过维纳滤波抑制灰度图中的噪声干扰。

4）对维纳滤波后的图像进行双三次插值，使得图像边缘更加平滑。

5）通过二值化处理将时频图像转换成黑白二值图像，凸显信号轮廓的同时降低图像矩阵数据量，最终得到224×224 像素的图像。

本节使用全阈值二值法来处理图像[15]。全局二值化阈值选择步骤如下：

1）获取图像中每个灰度值的出现概率。例如，Pix(0,i) 为 图像中第i 个 像素的灰度值，Pix(1,i)为第i个灰度值出现的概率。

2）计算灰度值的离散函数分布 H(i)。

6）将最大 WValve(i)值 中 i对应的灰度值作为全局二值化阈值。

1.2 时频图预处理

1.3 HOG 特征提取

在图像处理中，HOG 特征参数一般通过统计图像中的梯度信息来描述物体的局部纹理特征。HOG算子将图像分为若干个细胞单元（cell），其中每个cell中包含像素，计算像素的梯度和边缘的方向直方图，统计直方图并组合构成HOG 特征参数。由于梯度主要存在于边缘地区，该算法计算的局部区域梯度或方向边缘密度能够很好地描述图像中的线条边缘、拐点、形状及变化规律[16]。基于该思想，将HOG特征提取引入到时频图像分析中，以实现对时频域信号的边缘、形状和变化规律的检测。此外，信号经过1.1 节所述的MSST 时频变换和二值化后，时频聚集性更高，线条轮廓更加清晰，拐点更加明显，增强了HOG 算子提取有效梯度值作为特征参数的能力。具体的HOG 特征提取算法实现过程如下：

1）梯度的计算。在x 方向上，通过梯度算子[-1,0,1]对原图像做卷积运算，得到在 x轴方向上（向右为正方向）的梯度分量Gx(x,y)，再在 y 轴上用梯度算子[-1,0,1]T做同样的运算，可得 y轴方向（向上为正方向）的梯度分量Gy(x,y)，H(x,y)为图像像素值，如下：

2）梯度方向直方图构建。将梯度方向180°分成9 个方向块，如图3 所示，这9 个方向块对应的角度区域作为图4 直方图的横坐标，再统计每一个角度区域对应的梯度信息，得到梯度方向直方图。以表1 中梯度方向和梯度值为例，将像素的梯度值对应梯度方向角度映射到直方图中，将梯度值的投影权值作为梯度方向直方图的幅值，得到该cell 的梯度方向直方图，如图4 所示，最终统计直方图的9 个幅值作为对应cell 的9 维特征向量。其中，cell的边长为8，图像大小为224×224，则图像每一行有28 个cell，block 是由4 个cell 组成的正方形，通过block 在图像上移动进行特征提取，每次移动步长为1，则 一 幅 图 共 需 要 移 动（224/8-1）×（224/8-1）次，也就是需要移动27×27 次，因此可得一幅图的特征数为4×9×27×27=26 244 个。

图3 梯度方向分块Fig.3 Gradient direction block

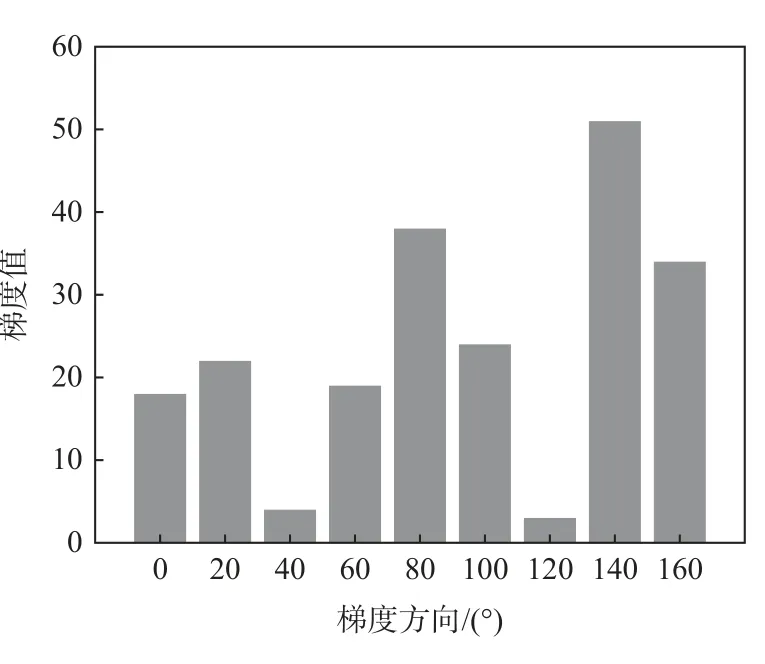
图4 方向梯度直方图Fig.4 Histogram of oriented gradient

表1 梯度方向和梯度值Table 1 Gradient direction and gradient values

1.4 PCA 降维

HOG 算子提取的特征向量维度较高，且存在大量的冗余信息，这些冗余信息会降低分类速度和识别精度。因此，可以通过式（27）所示的PCA 法对HOG特征向量进行降维处理。

式中：ZHOG表示提取训练正样本HOG 特征向量；YPCA表示降维后的特征向量。因此，最终特征向量为协方差矩阵 W 的前 K 个特征值 λ1,λ2,···,λK所对应的特征向量( YPCA1,YPCA2,···,YPCAK)。

2 识别算法流程

基于第1 节所述，雷达信号在经过MSST 后得到信号时频分布图，再在经过预处理后进行HOG特征提取，将提取的HOG 特征进行PCA 降维，最终采用SVM 分类器对雷达信号的特征参数进行分类。算法整体流程如图5 所示。

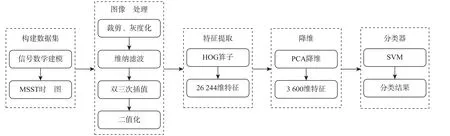
图5 算法整体流程Fig.5 Overall flow chart of the proposed algorithm

算法具体步骤如下：

1）对接收到的时域雷达信号进行时频变换得到MSST 时频图，并构建数据集。

2）将变换后时频图进行裁剪、灰度化、维纳滤波、双三次插值、二值化等图像预处理，减少噪声干扰和冗余信息，同时也降低数据计算量，并凸显信号轮廓。

3）对预处理后的图像进行HOG 特征提取，得到一组26 244 维的特征向量。

4）采用PCA 法对HOG 特征向量进行降维，去除冗余信息，提高识别速度。

5）通过SVM 分类器实现对特征向量的分类。

3 实验结果与分析

针对本文提出的雷达信号识别算法，从时频图对比、识别准确率、对比实验、鲁棒性分析4 个方面展开仿真实验。仿真实验的计算机硬件条件为：Intel(R) Core(TM) i7-10875H CPU @ 2.30 GHz 和16.0 GB RAM，GPU：NVDIA GeForce RTX 2060，仿真工具为MATLAB。本文还搭建了半实物仿真实验平台，针对实测数据进行了信号识别实验，以验证算法的有效性。

3.1 数据集设计

本文选取CW、LFM、BPSK、QPSK、2FSK、NLFM、LFM/BPSK、LFM/FSK 和FSK/BPSK 共9 种典型雷达信号进行实验。参数设置如下：采样频率为200 MHz，载波频率为20 MHz，脉宽为3.5 μs，带宽为15 MHz。其中，BPSK 信号采用7 位Barker 码；2FSK 有2 个频率点10 MHz 和30 MHz，复合调制参数设置与上一致。实验选取信噪比范围为-14～10 dB，步长为2 dB，每个信噪比下每种信号生成600张样本，其中400 张样本用于训练，剩下200 张样本用于测试，9 种信号共生成3 600 张训练集和1 800张测试集，实验中附加的噪声为高斯白噪声。

3.2 时频图对比

为了验证MSST 相比STFT 与SST 具有较好的时频聚集性，图6 给出了-4 dB 信噪比下BPSK 信号的STFT 时频图、SST 时频图及MSST 时频图。从图6（a）中可以看出，BPSK 信号相位跳变处信号发散，信号分辨率低，信号特性不明显，容易与CW信号混淆。从图6（b）中可看出，SST 变换后的信号分辨率相比于STFT 变换有一定的聚集性，但在相位跳变处发散仍然严重，而图6(c)中的信号经过MSST变换信号时频聚集度高，信号特征更加明显，相比于STFT 变换和SST 变换有更好的分辨率，有利于后续HOG 算子提取信号轮廓特征。

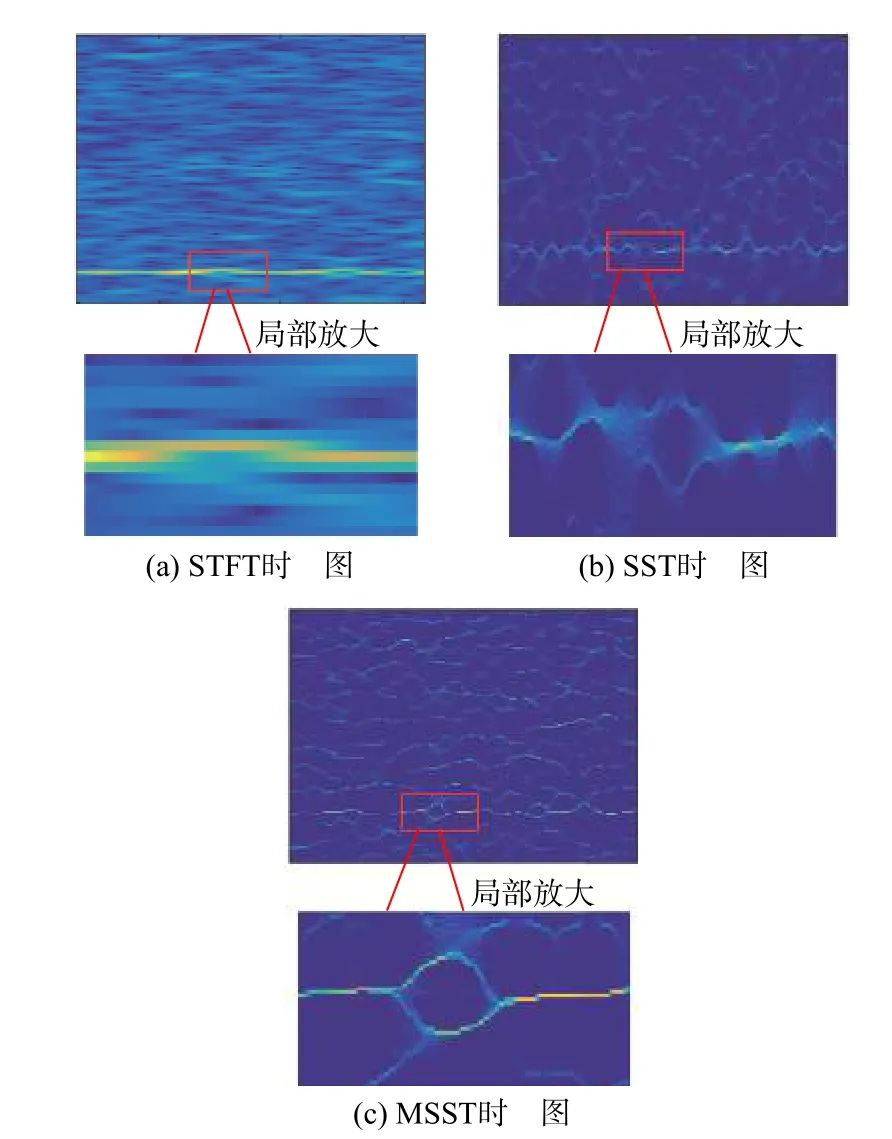
图6 STFT、SST 和MSST 时频图Fig.6 Time-frequency images of STFT, SST and MSST

3.3 识别准确率验证

根据第1 节和第2 节介绍的方法，通过对雷达辐射源信号进行时频变换、特征提取及分类识别实验来验证本文算法的识别准确率。图7（a）为本文算法在不同信噪比下的识别准确率折线图。可以看出，在信噪比不低于-8 dB 时，9 种雷达信号的整体识别准确率均在96%以上，当信噪比为-6 dB时，识别准确率接近100%。还可以发现，即使信噪比在较低的-10 dB 时，本文算法仍可以获得90%以上的较高识别准确率。这是因为信号经过MSST后时频得到压缩，信号线条更加明显，再经过图像二值化进一步凸显了图像信号轮廓信息，增强了HOG 算子提取有效梯度值作为特征参数的能力，从而提高了识别准确率。

图7 识别准确率Fig.7 Recognition accuracy

从图7（b）可以看出，当信噪比较低时，LFM/BPSK信号、BPSK 信号和LFM 信号识别准确率较低，通过分析图8 的混淆矩阵可知，信噪比为-10 dB 时，BPSK和CW、LFM 和LFM/BPSK 信号之间容易引起混淆，4 种信号识别准确率在80%左右。这是因为随着信噪比降低，噪声对信号干扰加强，使得时频图的有效信号特征减少，从而识别准确率下降。但随着信噪比增加，当信噪比为-4 dB 时，从图8 的混淆矩阵中可以看出，9 种信号识别准确率均达到99%以上。

图8 九种雷达信号识别准确率混淆矩阵Fig.8 Confusion matrix of recognition rate of 9 kinds of radar signals

3.4 算法对比实验

1）算法识别准确率对比

为了验证本文算法的良好性能表现，在同等条件下与对称Holder 系数法[13]、LBPV 法[17]及AlexNet模型[18]进行实验对比，实验结果如图9 所示。

图9 四种算法平均识别准确率对比Fig.9 Comparison of average recognition rates of four algorithms

由图9 可知，对称Holder 系数法抗噪性较差，在信噪比低于0 dB 时，分类器使用线性核或高斯核，识别准确率均低于75%，主要是时域信号受噪声影响较大，从而导致可提取的有效特征参数减少。本文使用的时频图经过图像预处理后，噪声更少，二维平面可提取的有效信息更多，识别准确率相对于对称Holder 系数法更高。LBPV 法使用的LBPV 算子随着时频图成像质量下降，特征区分度不强，识别准确率下降严重，在信噪比低于-6 dB时，识别准确率低于80%。而本文基于MSST 得到的时频图，频谱能量更加集中，时频图像更加精细，HOG 算子提取的特征也能更完整地表述信号，抗噪性能较好，因此在信噪比为-8 dB 时，9 种信号的整体识别准确率达到96%，即使在更低信噪比的情况下，算法仍然能保持较高的识别准确率。AlexNet模型在低信噪比下识别准确率相比于本文算法较好，但复杂度较高，且随着信噪比增加，识别准确率增长速率降低，当信噪比大于-6 dB 时，本文算法略高于AlexNet 模型。

2）算法训练与测试时间对比

SVM 相比于深度学习具有复杂度低和样本需求量少的优势。由表2 可知，AlexNet 模型训练时间较长，即使通过GPU 并行计算，模型训练时间依旧长于本文的SVM 模型。虽然本文使用的SVM模型训练样本较少，但在低信噪下依然有较高的识别准确率。较短的训练时间和良好的识别准确率使得SVM 广泛应用于工程应用中。

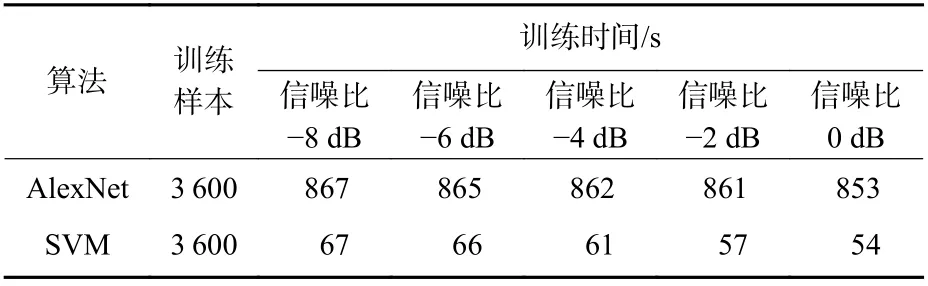
表2 算法训练时间Table 2 Algorithm training time

同时，为了验证本文算法具有较好的识别速度，实验选取-2 dB 下的测试集进行识别，重复多次运行本文算法、对称Holder 系数法[13]、LBPV 法[17]，求取每个算法的平均运行时间。从表3 可知，本文算法相比于LBPV 法识别速度更快，相比于对称Holder系数法运行速度略慢，但在低信噪比下，本文算法识别准确率高于对称Holder 系数法。

表3 算法识别时间Table 3 Algorithm recognition time

3.5 识别鲁棒性证明

本节进一步通过测试算法在混合信噪比下的识别准确率来验证算法的鲁棒性。在不同的信噪比下进行实验，训练集选取信噪比分别在-14 dB、2 dB、-2 dB、10 dB 条件下各生成3 600 个样本，测试集选取在-6 dB、10 dB、-10 dB、2 dB 下各生成1 800 个样本。混合信噪比实验信噪比从-14 dB 到10 dB 变化，步长为2 dB，训练集针对每种信噪比选取180 个样本，共为2 340 个样本，测试集针对各信噪比选取90 个样本，共1 170 个样本，实验结果如表4 所示。

表4 训练集和测试集在不同信噪比下的整体识别准确率Table 4 Overall recognition rate of training set and test set under different SNR

由实验可知，本文算法无论是在不同信噪比下还是混合信噪比下，信号的整体识别准确率都在90%以上，识别准确率较高，具有良好的鲁棒性。

3.6 半实物仿真实验

为了进一步验证本文算法的有效性，在实验室搭建了如图10 所示的雷达辐射源信号识别半实物仿真实验平台，以开展信号识别实验。半实物仿真实验平台基本参数为：支持最大收发信号带宽200 MHz，发送波形位宽14 bit，接收波形位宽16 bit，中频采样率3 GSa/s，C 波段。

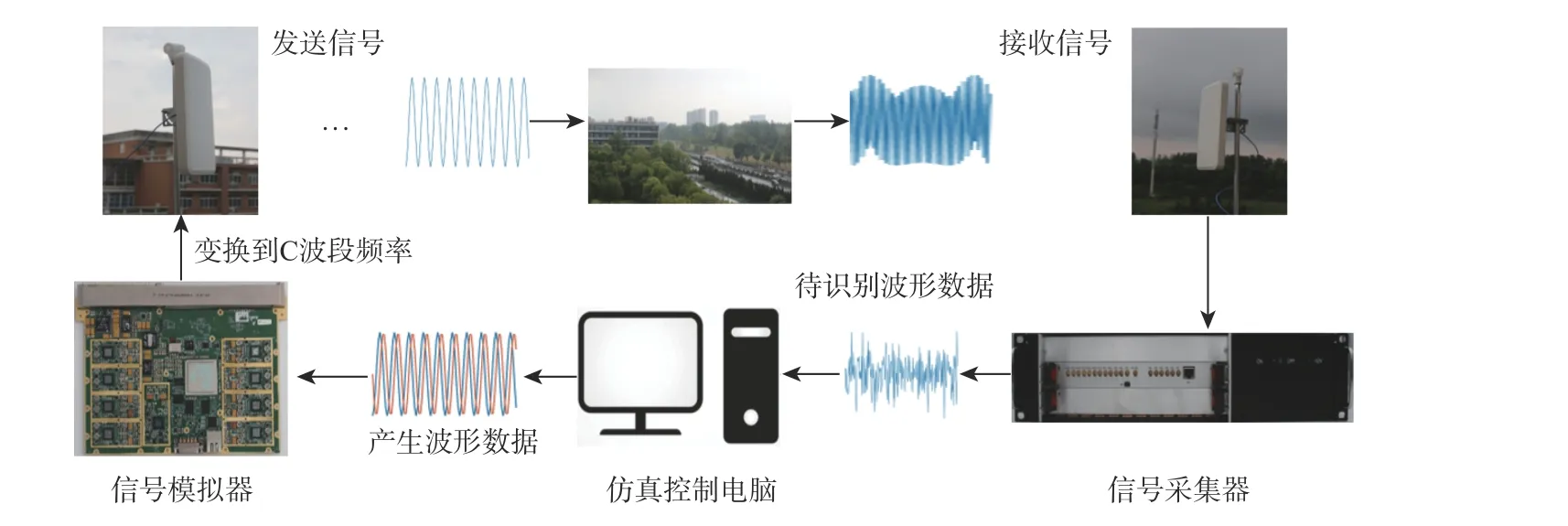
图10 雷达辐射源信号识别半实物仿真实验平台Fig.10 Hardware-in-the-loop simulation experiment platform for radar radiation source signal recognition

所搭建半实物仿真平台由仿真控制电脑、信号模拟器和信号采集器构成。仿真控制电脑生成5 400 个波形，信号调制类别随机分布，并对每个波形进行标注，再将这些波形数据按照一定间隔发送到信号模拟器，完成数模变换，变换到C 波段频率，并通过天线发射到空旷区域；同时仿真控制电脑控制信号采集器，采集天线接收到的信号，并且经过下变频、模数变换、脉冲提取后，生成待识别波形数据集；最终按照本文算法进行识别。图11 给出了半实物仿真实验得到的识别准确率曲线，并与3.3 节实验结果做了对比。

从图11 可看出，半实物仿真实验整体识别准确率略低于仿真实验识别准确率。其原因在于：半实物仿真实验所采集到的数据由于受到电波传播信道的影响，信噪比会存在一定波动，并且经传播的信号存在衰落，造成MSST 时频图像的变形，最终影响了识别准确率。但在较低信噪比下，半实物仿真依然具有较高的识别准确率。当信噪比为-8 dB时，半实物仿真实验的识别准确率能达到94%，当信噪比为-2 dB时，识别准确率接近100%，表明本文算法在较为逼真的工程应用环境中也具有较好的识别准确率。

图11 基于半实物仿真实测数据的识别准确率Fig.11 Recognition accuracy based on hardware-in-the-loop simulation data

4 结 论

1）针对低信噪比下雷达辐射源信号识别任务，采用HOG 特征对雷达信号MSST 时频图进行特征提取，并使用PCA 进行降维，最终通过SVM 实现有效分类。

2）通过对比实验可知，本文算法识别性能较好，计算复杂度低。

3）采用半实物仿真实验进行验证。实验结果表明，本文算法在低信噪比下对典型雷达信号具有较高的识别准确率，为复杂电磁环境下的雷达信号识别提供了一种可行方法。