端面密封材料S-07 不锈钢滑动摩擦学行为的分子动力学模拟*
王 权 庄宿国 黄 丹 朱正兴 刘秀波
(1. 中南林业科技大学材料表界面科学与技术湖南省重点实验室 湖南长沙 410004;2. 西安航天动力研究所 陕西西安 710100)
随着机械端面密封在航天航空等领域的广泛应用, 对其在特定工况下的性能提出了更高要求。 其中, 航天领域液氧煤油发动机的端面密封通常在高pv值(p: 压力,v: 速度)、 宽转速区间内运行, 并且服役时间长, 容易导致端面密封失效、 介质泄漏等问题, 存在一定的安全隐患[1-6]。
为了提高端面密封摩擦副材料的摩擦学性能及工作稳定性, 国内外研究者已进行了大量研究和试验。目前对于端面密封摩擦副性能的优化主要集中在其机械结构方面, 改善摩擦副接触条件或传动过程, 以匹配各种工况需求[7-9]。 如ZHOU 和ZOU[10]运用有限元分析的手段, 探究了压力、 转速对端面密封性能的影响。 但是对于该部件微观尺度下的运动过程及对应机制研究较少。
S-07 不锈钢作为一种航天发动机用端面密封材料,是一种马氏体-奥氏体双相镍铬不锈钢, 具有高强高韧和耐蚀性优良等特点, 其化学成分如表1 所示[11]。

表1 S-07 不锈钢化学成分[11]Table 1 Chemical composition of S-07 stainless steel[11]
机械端面密封在服役时, 接触面紧密接触且接触应力较大, 此时, 可将微观尺度下的接触行为视为诸多粒子相互作用。 分子动力学(Molecular dynamics,MD) 模拟是一种在纳米尺度上研究材料变化的工具, 它基于牛顿经典力学的计算方法, 从统计力学的基本原理出发, 能够在微观的分子甚至是原子层面,在计算机中仿真得到能量、 温度、 应力等物理量, 进而推导出工程问题所需的摩擦学参数[12-14]。 MD 模拟因其能从原子运动角度对材料体系进行系统模拟和计算, 现已广泛运用于研究医药、 化学、 材料表面工程等科学研究领域[15-19]。 张宏亮等[20]利用MD 模拟通过改变滑动速度、 距离及外加载荷, 研究了纳米单晶铜的磨料磨损行为, 发现纳米单晶铜内部缺陷及表层单晶铜原子的磨料磨损行为有较大差异。 YANG等[21]通过MD 模拟软件, 模拟了AlCoCrFe 高熵合金涂层的力学和摩擦学性能, 模拟测试计算的弹性模量、 纳米硬度、 摩擦因数和磨损体积均与试验所得数据保持一致。 LI 等[22]采用分子动力学方法研究了铜基高熵合金涂层的摩擦磨损行为, 运用位错萃取分析(Dislocation extraction analysis, DXA) 和共近邻分析(Common neighbor analysis, CNA) 分析晶格结构和位错, 发现高熵合金涂层可以有效地释放应力, 降低铜基材料的损伤。
目前已经有很多学者采用MD 模拟对各种材料的摩擦学性能进行了研究, 但大多数模拟过程中, 都是采用金刚石刚体模型等作为对偶件, 研究摩擦过程中原子运动、 位错及应力等信息。 但是, 结合工件实际工作场景, 选择常见的对偶件结构模型进行模拟, 可以使模拟结果对于实际应用更具有直观参考价值。
本文作者将分子动力学模拟技术应用于S-07 不锈钢端面密封材料体系, 基于发动机工况特征, 选择同种材料作为摩擦副, 通过改变摩擦过程中压入深度、 滑动速度等参数, 模拟其磨损量、 摩擦因数等摩擦学性能, 探索其摩擦磨损机制, 并基于此提出合理有效控制及改进方案, 以期提高端面密封材料的可靠性。
1 模型和势函数
在S-07 不锈钢分子动力学模拟建模过程中, 从S-07 不锈钢的组成元素Fe、 Cr 和Ni 入手, 建立密封材料S-07 不锈钢的结构模型。 具体操作过程如下:
(1) 建立S-07 不锈钢的原胞模型, 按照质量分数为78.24% (Fe)、 16.45% (Cr)、 5.31% (Ni)将Fe、 Cr、 Ni 这3 种原子随机填充到点阵中;
(2) 对建立好的模型进行几何结构优化以及能量最小化处理;
(3) 选择优化结束后能量最低的S-07 不锈钢原胞模型扩胞建立S-07 不锈钢模型。
为符合所建立结构模型的部分设定, 消除边界效应, 在其X、Y轴方向上设定周期性边界条件, 在Z轴方向上设定非周期性边界条件, 模型尺寸大小为17.873 8 nm×8.419 6 nm×3.889 8 nm, 共有43 200 个原子, 其中包含Fe 原子33 480 个, Ni 原子7 560 个,Cr 原子2 160 个, 对偶件模型尺寸大小为5.957 9 nm×2.806 5 nm×1.944 9 nm, 将其设置为刚体。
经过上述过程, 建立的目标S-07 不锈钢的结构模型, 如图1 所示。
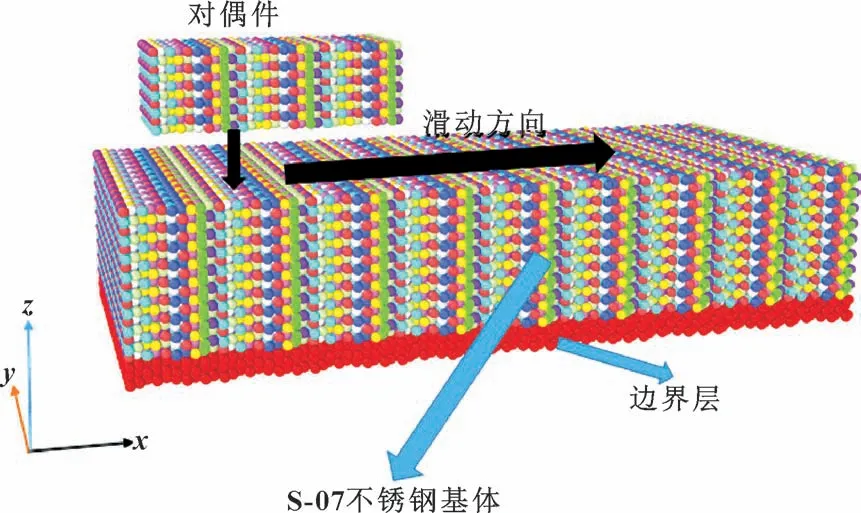
图1 S-07 不锈钢分子动力学模拟结构模型Fig.1 S-07 stainless steel molecular dynamics simulation structural model
随着MD 模拟技术的不断发展, 已经有较为成熟的势函数来描述金属原子间的相互作用, 如嵌入原子势(Embedded-atom method, EAM) 等。 文中模拟计算时, 采用EAM 势函数描述模型中Fe-Cr-Ni 原子之间的相互作用[23]。 其势函数如下:
式中:Ei为系统的总势能;F为原子的电子密度ρ的函数;ρi为除i外其余原子在i处产生的电子云密度的和;ϕ为对势项;rij为i原子和j原子之间的距离。
2 数值模拟
MD 模拟具体步骤如下: (1) 建立所需结构模型; (2) 优化结构模型参数; (3) 给定初始条件;(4) 开始模拟, 计算模拟运动过程中的宏观物理量。文中研究采用LAMMPS 模拟计算软件、 OVITO 可视化软件, 实现MD 模拟, 并进行可视化处理, 便于直观研究模拟的进程。
为了有效利用计算资源, 选取时间步长为1 fs。考虑到端面密封摩擦副材料的摩擦磨损过程, 选取相似于S-07 不锈钢模型的另一模型作为对偶件, 以压入深度和滑动速度为变量, 进行摩擦磨损试验模拟,分析S-07 不锈钢的摩擦磨损性能。 在模拟加载之前,要对构建的结构模型进行优化, 采用共轭梯度算法(Conjugate gradient algorithm) 最小化整个结构模型的能量, 消除模型中不合理的结构。 为了使模型达到平衡状态, 采用正则系综(Canonical ensemble, NVT)方法, 将模型初始温度设为300 K 以用于后续计算。
对S-07 不锈钢的摩擦磨损性能模拟分为两个阶段。 在第一阶段, 对偶件以0.01 nm/ps 的速度进入模型, 达到预定压入深度; 在第二阶段, 以预定的滑动速度沿X正方向滑动。 在这两个阶段中, 模型整体温度保持在300 K, 在NVT 系综下进行模拟。 仿真结果使用OVITO 软件对模型进行可视化, 模型及仿真环境参数如表2 所示。
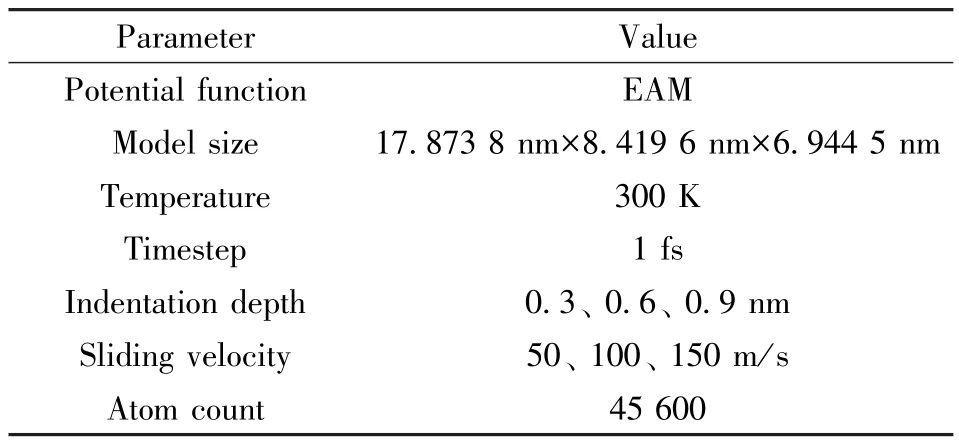
表2 模型和仿真条件参数Table 2 Model and simulation environment parameters
3 实验结果与分析
3.1 摩擦因数分析
对偶件受到的力是材料磨损性能的具体体现, 最重要的性能值就是摩擦因数, 而摩擦因数与对偶件的切向力和法向力密切相关, 因此分析摩擦因数是研究材料减摩性能的一个重要方向。 文中利用LAMMPS软件中compute 功能, 将对偶件受到的摩擦力与法向力的比计算为摩擦因数, 如式(3) 所示, 其中μ为摩擦因数,Fx为摩擦力,Fz为切向力[24]。
绘制对偶件在不同参数条件下的摩擦因数曲线如图2 所示。
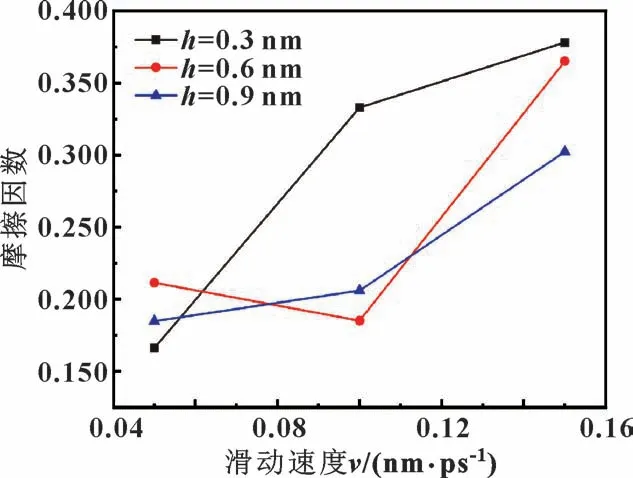
图2 不同压入深度下对偶件的平均摩擦因数随相对速度的变化Fig.2 Variation of average friction coefficient of the friction pair with relative velocity under different indentation depth
从图2 中可知, 在0.3、 0.6、 0.9 nm 压入深度下, 随着相对滑动速度增加, 摩擦因数均呈现上升趋势。 在S-07 不锈钢与对偶件的相对滑动过程中, 对偶件先压入表面, 然后与不锈钢发生相对滑动; 期间, 对偶件与不锈钢表面存在剪切作用, 不锈钢表面发生弹性和塑性变形。 当作用在不锈钢表面的机械能足以破坏S-07 不锈钢原子间的金属键后, 不锈钢原子就会随对偶件一起滑动, 进而被磨损去除形成磨屑。 摩擦因数增加是因为在单位时间内, 所需要破坏的金属键更多, 从而表现为摩擦因数上升。
3.2 磨损形貌分析
不同参数下的模拟磨损表面形貌如图3 所示, 其中图3 (a)、 (b)、 (c) 分别代表压入深度为0.3、0.6、 0.9 nm 时磨损表面形貌。 由图3 (a)、 (b) 可知, 当对偶件滑动速度为50 和100 m/s 时, 磨损表面较滑动速度为150 m/s 时更为粗糙。 由图3 (c)可知, 当对偶件压入深度为0.9 nm 时, 滑动速度为150 m/s 时, 不锈钢磨损表面形貌较滑动速度为50 和100 m/s 时更为粗糙。
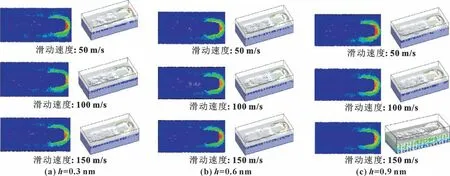
图3 压入深度为0.3、 0.6、 0.9 nm 时不同滑动速度下表面磨损形貌Fig.3 Surface wear morphologies at different sliding velocity when the indentation depth is 0.3 nm (a), 0.6 nm (b), and 0.9 nm (c)
当对偶件压入S-07 不锈钢然后发生相对滑动,在不锈钢表面留下一道划痕, 部分不锈钢表面原子在力的作用下发生弹性变形和塑性变形, 被对偶件挤压出不锈钢表面。 一些不锈钢原子在对偶件运动方向正前方和两侧堆积形成磨屑原子, 当对偶件经过某一位置后, 部分被挤压的磨屑原子回到原来位置, 部分变形得到恢复。
为计算磨损体积损失, 导出S-07 不锈钢在不同参数下摩擦磨损试验后的模拟磨损轨迹, 使用OVITO 软件的构建表面网格(construct surface mesh) 对磨损轨迹进行表征, 选择alpha-shape method 下的identify volumetric regions 选项工具对磨损区域进行识别和展示, 并计算磨损体积。
图4 所示为滑动速度为50、 100、 150 m/s 时不同压入深度下的磨损体积变化。 可知, 在滑动速度一定的情况下, 对偶件压入深度越大, 不锈钢的磨损量越大。 这是由于随着对偶件压入深度的增加, 在对偶件的作用下产生了更多的不锈钢原子脱离原来的位置堆积形成磨屑, 伴随对偶件一起滑动。 随着滑动速度的增大, 体积磨损量大体上呈现出下降趋势; 根据牛顿运动定律, 在相同的位移下, 静止的原子获得更大速度需要更大的驱动力, 随着速度的增大, 部分原子未能获得较大的速度, 无法与对偶件共同运动, 导致磨损量下降。

图4 不同滑动速度和不同压入深度下S-07 不锈钢体积磨损量Fig.4 The wear volumeof S-07 stainless steel under different sliding velocity and indentation depth: (a) 50 m/s; (b) 100 m/s; (c) 150 m/s
3.3 位错分析
当S-07 不锈钢与对偶件发生相对运动时, 在材料表面下方会发生亚表面损伤, 其损伤程度可以用统计分子动力学模拟中的位错密度来表征, 位错密度为位错长度与材料体积的比。 研究中所使用的模型体积大小不变, 所以位错长度所体现的变化趋势与位错密度变化趋势一致。 采用OVITO 软件中Dislocation Extraction Analysis (DXA) 模块用于计算位错线的长度。 图5 所示为压入深度为0.3、 0.6、 0.9 nm 时不同滑动速度下位错线的长度变化。 可见摩擦滑动速度与位错线长度大体上呈现负相关, 当滑动速度较低时, 位错线长度相对较长; 另外, 随着相对滑动距离的增加, 大多数位错线长度呈现上升趋势, 预示随着滑动距离的增加, 亚表面损伤程度增加, 内部缺陷增多; 但压入深度为0.6、 0.9 nm 和滑动速度为150 m/s时, 滑动距离为2~4 nm 时, 位错线长度呈下降趋势。

图5 不同压入深度和滑动速度下位错线长度随着相对滑动距离变化Fig.5 Variation of the length of dislocation line with relative sliding distance under different indentation depth and sliding velocity: (a) 0.3 nm; (b) 0.6 nm; (c) 0.9 nm
选压入深度为0.6 nm、 滑动速度为150 m/s 作为例子进行了分析, 结果如图6 所示。 从图6 (a) 可知, 在滑动距离为2 nm 时, 存在5 条特殊的位错线1/3<1 0 0 >, 这种位错线被称为Hirth 位错。 由于Hirth 位错的滑移方向不在密排平面上, 很难滑动,因此它也被称为Hirth 位错锁。 从图6 (b)、 (c) 可知, 在滑动距离增加到4 nm 过程中, 位错线长度下降。 分析图7 可知, 在Hirth 位错上方存在低应力区,由于这个区域的存在, 降低了应力, 因此不会通过产生大量新的位错来释放应力; 原本存在的位错逐渐向表面移动并消失, 导致位错线长度下降; 在滑动距离为4 nm 之后, Hirth 位错与高应力区靠近, Hirth 位错获得能量并分解为Shockley 位错。 位错锁消失后,应力上升, 不锈钢材料继续产生位错来释放应力, 因此位错线长度又呈现上升趋势。
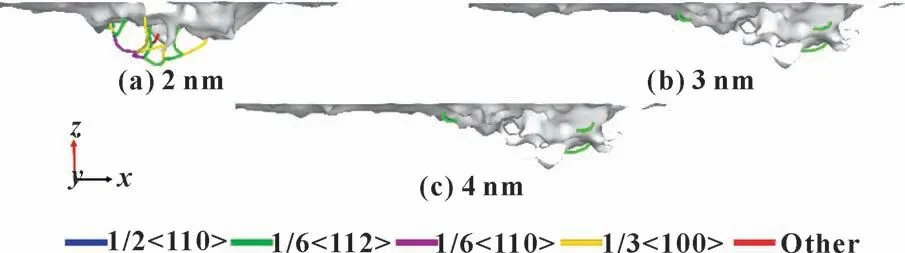
图6 不同滑动距离下位错分布(h=0.6 nm, v=150 m/s)Fig.6 The dislocation distribution under different sliding distance(h=0.6 nm, v=150 m/s): (a)2 nm; (b)3 nm; (c)4 nm

图7 不同滑动距离下应力分布(h=0.6 nm, v=150 m/s)Fig.7 The stress distribution under different sliding distance (h=0.6 nm, v=150 m/s): (a) 2 nm; (b) 3 nm; (c) 4 nm
4 结论
通过分子动力学模拟研究S-07 不锈钢滑动摩擦磨损过程, 探究在不同滑动速度、 压入深度下S-07不锈钢摩擦因数变化规律、 表面磨损形貌特征以及内部位错演变过程及相关机制。 主要结论如下:
(1) 随着摩擦滑动速度的上升, 摩擦因数均增大, 这是由于在单位时间内需要破坏的金属键更多,导致摩擦因数变大。
(2) 磨损量大体上与滑动速度呈负相关, 原因在于随滑动速度上升部分原子无法与对偶件一起协同滑动形成磨屑。
(3) 滑动摩擦速度与位错线长度大体上呈负相关, 当滑动速度较低时, 位错线长度相对较长; 当滑动距离为2~5 nm, 速度为150 m/s 时, 由于Hirth 位错和低应力区共同作用的原因, 导致位错线长度出现先下降后上升。

