基于Triangle 的道路测量模型快速生成技术研究

范舒畅，孙 颖，曹先革，汤 敏，刘旭东

（1.广东省交通规划设计研究院集团股份有限公司，广东 广州；2.东华理工大学测绘工程学院，江西 南昌；3.宁波冶金勘察设计研究股份有限公司，浙江 宁波）

引言

三维地面模型发展至今已有数十年的历史，其最早可追溯于上世纪50 年代Miller 教授在公路设计上的应用。随着计算机技术的飞速发展，截至今日已涌现出了很多成熟的模型[1]。宋占峰等提出的插入点约束边理论巧妙剔除了道路设计面内地形点问题[2]，蒲浩等基于双三次混合孔斯曲面片理论有效解决了模型间的拼接问题[3]。现有的模型理论虽然解决了建模中的大部分问题，但在道路模型建立的细分领域仍存在着操作过程复杂、集成度低、人工干预多等问题。

本研究将基于Triangle，探讨快速建立道路模型的数据组织方法及关键技术流程，最后在梅南互通立交项目上应用。为道路测量模型的快速建立、测量成果的高效检查等应用研究领域提供参考。

1 数据及方法

1.1 实测数据

道路等带状地形图测绘通常采用人工逐点实测的方式进行（“实测数据”），其测量结果能够较为真实的反应出道路的边界范围及地形变化情况，因此实测数据在道路模型建立过程中应作为约束条件。

自定义后缀为tzx 的文本文件按指定格式以实测特征线为单位对实测数据进行存储，其第一行依次记录特征线的颜色索引、节点数、类别名，从第二行开始依次记录各节点坐标值，直至记录完该特征线的全部节点。

1.2 点云数据

多源数据融合的三维建模方法可以综合多种数据的优点，不仅能使得模型的精度达到项目要求，还能大大提高建模效率[4]。故点云数据对于道路模型精细化建立是十分必要的。由于点云数据量庞大，常规的可视化查找、编辑等操作将十分困难甚至不能实现。

“分块分级”法以自定义矩形为单位进行分块存储，矩形范围内点云数据标准化块文件名为：Xmin-Xmax-Ymin-Ymax.xyz（分块存储）。该命名依次记录了X 与Y 坐标的极值。根据图面待编辑点云的坐标范围即可在分块点云文件集中快速定位到目标点云文件。最后以文件流的方式实现目标点云的快速编辑（分级处理）。该法有效避免了海量点云数据的重复查找，降低了计算机内存的开销，提升了点云编辑效率。“分块分级”流程见图1。

图1 “分块分级”流程

1.3 三角剖分与优化

1.3.1 数据组织

Poly 文件（见表1）是由“点”、“线”及“洞”三部分顺次拼接而成的自定义文本文件。“点部分”第一行记录点总数、维度、属性及边界标记（0/1 表示），从第二行至结尾依次记录点索引、X 坐标及Y 坐标；“线部分”第一行记录线总数及边界标记（0/1 表示），从第二行开始至结尾依次记录边索引及每条边所对应的端点在“点部分”中的索引；“洞部分”需动态记录挖孔区域内一点的坐标。

表1 poly 文件格式

1.3.2 三角剖分

“三角剖分”即将给定的数据点集按照某种规则进行三角化处理并生成三角网的过程。在所有可能的三角网中，一般情况下Delaunay 三角剖分的结果被公认为是最优的三角网[5-6]。数据冗余度小、简单易更新的Bowyer-Watson 算法是最为常用的Delaunay 三角剖分算法。基于C 语言的开源二维质量网格生成器Triangle 通过参数控制的方式可快速按Bowyer-Watson 算法生成Delaunay 三角网。凭借着出色的稳定性及扩展性，Triangle 长期以来被广大学者作为三角组网的首选工具。

1.3.3 长度标尺

1.3.4 无量纲半径

三角形外接圆无量纲半径是衡量一个三角形偏离正三角形的严重程度。三角形外接圆无量纲半径越大，该三角形偏离正三角形越严重。因此无量纲半径是计算机自动计算内插点从而改善网格形状的重要判断依据。设三角形ΔABC 的外接圆半径为r，外接圆圆心长度标尺为L，则外接圆无量纲半径R 计算式为：

由式（3）可计算得到正三角形的无量纲半径为2/3。

1.3.5 优化策略

将三角网中的三角形逐个计算外接圆圆心的长度标尺L、外接圆半径r 以及外接圆无量纲半径R；然后将三角形以R 为索引倒序排列，向序列顶部R 最大的三角形外接圆圆心处插入新点Q；随后按照Bowyer-Watson 算法进行局部网型重组，将新生成的三个三角形与原三角形按R 值再次排序后重复前述操作，直至序列顶部的三角形外接圆无量纲半径R<1。

三角网的优化在网格加密、提升网格质量方面是十分必要的，但点云数据的加入通常使生成的三角形数量十分巨大，因此对全部的三角形进行优化是不现实的。故在道路等带状地物建模过程中三角网优化必须进行取舍或只在局部进行。

经过多次测试，总结并得到优化原则如下：

第一，包含实测特征线的三角形一律不进行优化。

第二，三角网边缘三角形的无量纲半径阈值设置为1.3～1.5。

2 案例应用

本研究将以梅南互通立交定测项目为例按前述理论进行道路模型的快速构建。梅南互通立交位于梅州市梅县区梅南镇内，互通立交范围内主线最小平曲线半径为1 000 m，新建匝道最小平曲线半径为70 m，各匝道平纵指标均满足设计速度所对应匝道设计标准。新建匝道总长2 361.131 m（不含劝返车道长度）。

图2 为梅南互通立交模型快速建立的关键技术流程，具体可分为如下6 个步骤编程实现：

图2 道路测量模型建立流程

①绘制并提取实测数据。

②“分块分级”预处理点云数据。

③实测与点云数据融合生成Poly 文件。

④Triangle 三角剖分Poly 文件。

⑤遵循优化策略原则优化三角网。

⑥渲染优化三角网。

图3 所示为梅南互通立交定测项目的快速构模过程。其中（1）为实测数据绘制的2d 平面图，（1）到（2）实现了道路模型的三角剖分，（2）到（3）完成了三角网的剔除及优化，（3）到（4）完成了模型的渲染。模型最终效果满足生产部门的实际需求。

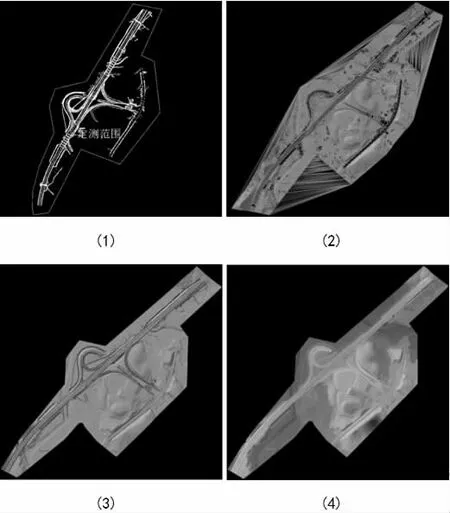
图3 梅南互通立交模型阶段图

3 结论

本研究基于Triangle，探讨了快速建立道路模型的数据组织方法及关键技术流程，最后在梅南互通立交项目上应用，总结如下：

（1）“分块分级”法对于海量点云数据的预处理具有较好的效果，有效避免了海量点云数据的重复查找，降低了计算机内存的开销，提升了点云编辑效率。

（2）改进的三角网优化策略对带状模型的网型优化及构建速度的提升有帮助。

（3）Triangle 具有较高的三角剖分效率及较好的扩展性与兼容性，可作为类似项目开发的底层工具。

本研究方法可应用于新建道路及道路改扩建等大范围带状地物建模领域中，方法提高了模型建立的速度，降低了模型建立的主观性偏差，保证了模型建立的一致性、准确性，为后续基于模型的操作奠定基础。