面向多目标资源受限的航空维修保障工序调度方法研究

魏梦媛，渠怀赓，孙 坤

（中国飞行试验研究院，陕西 西安）

引言

资源受限工序调度问题(Resource-constrained Project Scheduling Problem,RCPSP)是指在满足项目时序要求和多种资源的约束下，确定所有任务的开始时间及结束时间，使得总时间最短[1]。合理地调节各项目活动的开始时间和资源使得能够有效地缩短项目完工时间，在实际航空维修保障过程中具有非常重要的意义。目前这类问题的研究主要集中在工期单目标优化问题上[2]。实际航空维修保障中，单一指标难以评价方案优劣，需考虑多个指标并进行权衡，本文将维修保障人力资源的合理配置作为工序调度问题的目标，考虑维修人员数量的情况下，兼顾维修工序的紧前约束条件，基于RCPSP 构建维修保障时间和资源配置的多目标优化函数，采用快速非支配排序遗传算法(NSGA-II)对案例进行求解分析，实现在合理安排人力资源对工序进行维修的同时，维修时间最短，即合理利用维修资源，尽快完成维修任务。

1 修保障资源均衡多目标优化数学模型

资源受限情况下，实现航空维修保障过程时间最短、资源合理配置，可以归结为多目标优化问题。

此类问题的数学描述如下

针对实际航空维修保障过程，主要从维修工序、维修时间、维修人力资源3 个方面构建优化模型：优化目标为时间最短、人力资源合理配置；约束条件为资源数量和维修工序紧前约束条件。

1.1 目标函数

1.1.1 维修时间最短目标

假设一个维修项目中包括N 个工序，其中活动1和活动N 为虚拟活动，分别作为项目的开始和项目的结束。

T 为总时间，则目标函数为

以人力资源需要量的标准偏差作为均衡配置评价函数，数学模型表达如下

将Q 作为评价资源配置均衡的目标函数，当Q 越小，维修人员分配的拥挤程度越低，人员调配使用越合理，目标函数为

1.2 约束条件

维修保障过程中存在2 种约束关系：一是维修人员的数量约束，即对工序中任意时刻，正在进行的工序的维修人员总数，不超过限制的数量；二是紧前约束关系，即两个工序具有必然的先后关系[3]。如工序1和工序2 具有紧前约束关系，则工序2 的开始时间晚于工序1 的结束时间。

在整个维修项目中有如下假设：

a.单个工序的活动具有连续性，不存在停顿；

b.各工序紧前关系保持不变；

c.各种资源之间相互独立，不存在相关关系。

维修保障资源分配数学模型构建可以描述如下：一是维修人员须按照维修手册内容逐步完成所有工序，在前一项工作还没有完成的情况下，不能进行下一步活动；二是维修人员总数有限，每步工序所需维修人员数量是一定的，同一时刻进行的所有工序所需要的维修人员的数量之和应不大于总的维修人员数量；三是维修人员只有在进行完上一步维修活动后，才可以继续下一项，不能同时进行两项维修活动；四是总的维修时间的约束，完成最后一项维修保障活动的时刻T 不能大于总的维修保障时间，T 即为实际总维修保障时间。数学模型可以描述为

式（6）表示所有的最早、最晚开工时间应满足工序排布逻辑条件，且资源利用在受限范围内。

2 基于NSGA-II 的多目标优化算法

以上优化模型为多目标规划问题，一般不可能存在一个使每个目标都达到最优的解，本文选择快速非支配排序遗传算法-NSGA-II 作为多目标优化算法，可以得到一组均衡解，称为最优非劣解集或Pareto最优解集[4]。

NSGA-II 算法的基本思想如下。

第一步随机生成大小为N 的初始种群，对该种群进行非支配排序，再根据遗传算法，进行选择、交叉、变异操作，可以得到第一代子代种群；从第二代子代种群开始，合并父代种群与子代种群，进行快速非支配排序，计算拥挤度，包括非支配层的所有个体，根据个体之间的关系和拥挤度，选择出有优势的个体，形成新的父代种群；再重复第二步，通过遗传算法中的选择、交叉、变异操作形成新的子代种群，直到达到设定的循环数，或达到符合结合的条件[5]。

NSGA-II 算法主要的优化策略包含以下3 个方面。一是快速非支配排序，这一步根据个体的优势排列将种群中个体排序；二是拥挤度比较算子，根据个体拥挤程度选择进入下一代进行循环迭代的个体，保持种群多样性；三是精英保留策略，对应第二步，合并父代和子代个体再优先选择优秀个体，作为下一代种群，这一步能够保留历代计算出的最优个体。NSGA-II算法流程见图1。

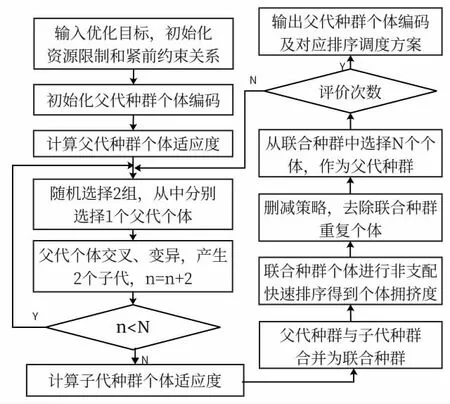
图1 NSGA-II 算法流程框图

3 基于isight 平台构建的多目标优化流程

以吊舱软管更换试验为例进行分析。机务维护人员总数量为8 人。在吊舱拆卸试验工序中，B、C、F，G四个工序属于可并行工作。根据据紧前工序排列原则，得到各工序的最早开工时间和最晚开工时间，并按实际工作中统计的各工序持续时间与人员数量，给出表1 中的试验流程逻辑关系。

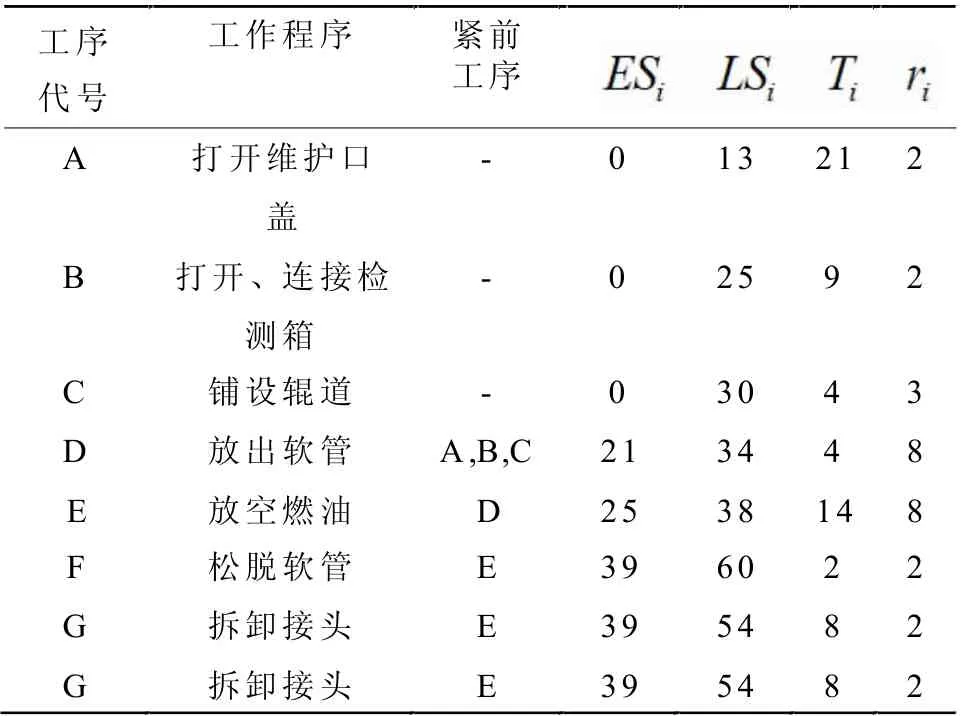
表1 专项试验流程逻辑关系及时间表

在Matlab 软件中，对前文中给出的优化目标和约束条件指标进行编程求解。

对多目标函数的优化设计，采用Isight 封装的NSGA-II 方法。以Isight 软件为平台，集成Matlab 软件完成并联机构的多目标优化。如图2 所示，搭建并联机构多目标优化流程图，箭头为数据和过程传递路径。

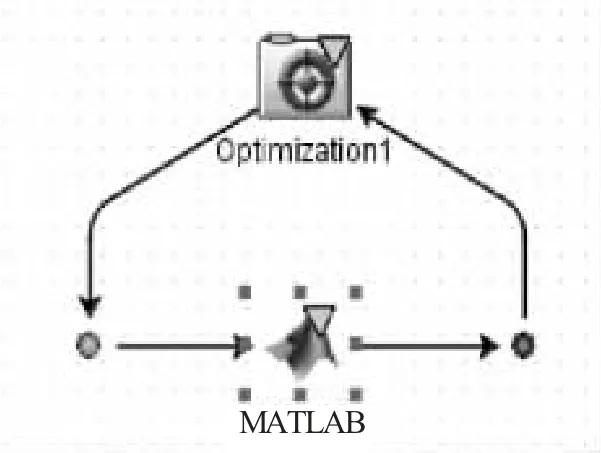
图2 ISIGHT 调用Matlab

通过多目标优化最终得到可行的设计点，对结果的选择提供重要的参考。图3 中可以看出可行点和不可取的劣解的分布。各设计点数值见表2。表2 的6 组结果中，后3 组结果均为较优，其中第6 组的资源均衡评价指标Q 与总时间T 都为最小，对应最优情况。

图3 可行解与最优解

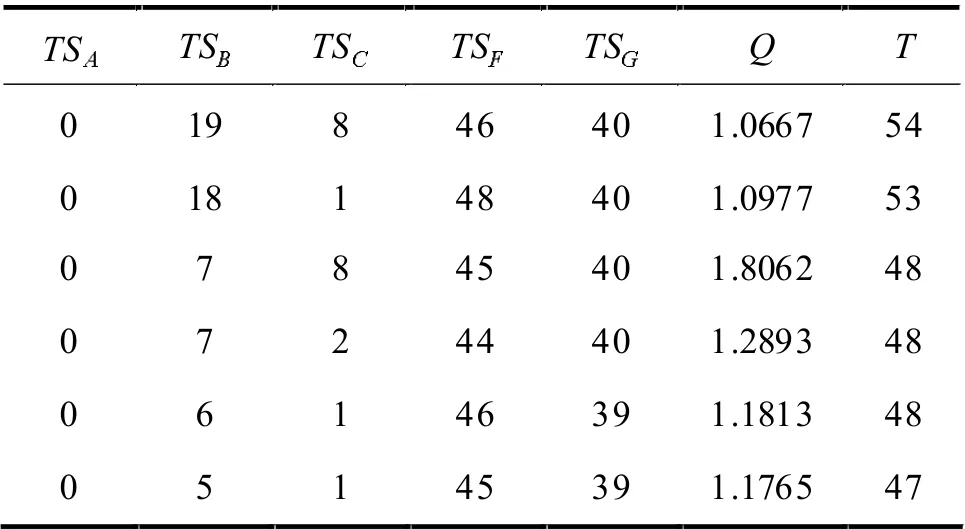
表2 优化结果及相应工序排列情况

优化前和优化后共7 组结果见图4。

图4 优化结果对比

图4 中第一组数值为优化前的目标值，可以看出，通过多目标优化，对工序进行调度排布，使得维修保障时间逐渐缩短，其中最优组时长为47 min，人员标准偏差也相应达到了低区间，这说明整个过程对于人力资源的配置实现了均衡优化。

4 结论

本研究针对航空维修保障过程中资源受限情况，构建了资源约束与维修保障时间最短、人力资源均衡配置多目标数学优化模型，结合NSGA-II 多目标优化算法，在Isight 平台中实现维修保障资源均衡多目标优化流程，可以达到时间缩短、资源均衡配置的目标。本研究提出的方法可以为航空维修保障工序调度提供参考。