适用于复杂流动的热气动弹性降阶建模方法

王梓伊，张伟伟，刘磊，*，杨肖峰

1．中国空气动力研究与发展中心 空气动力学国家重点实验室，绵阳 621000

2．西北工业大学 航空学院，西安 710072

更高、更快、更远一直是飞行器发展的主旋律。近年来，随着超燃冲压发动机技术的逐渐进步，以其 为 动 力 的X-43［1］、X-51［2］等多型高超巡航演示验证飞行器试飞成功，大型高超巡航飞行器更是成为了行业研究热点。而此类飞行器由于飞行马赫数高、几何构型复杂，其面临着严酷的气动热/气动弹性强耦合服役环境［3］。特别是在气动加热作用显著的迎风面区域，结构升温造成材料物性变化，以及大温差造成的热应力，可能引发结构颤振安全边界降低等严重的热气动弹性问题。

热气动弹性问题［4］是交叉融合了空气动力学、气动热力学、结构热传导、结构动力学等学科的复杂多物理场耦合问题。典型热气动弹性现象包括：机体/部件静变形、翼舵颤振/抖振、壁板颤振等［5］。这些现象具有高度危险性，可能导致飞行器结构变形、振动、破坏和失控。随着飞行器结构质量系数逐渐降低以满足日益严苛的设计要求，薄壁结构和轻质材料的大量使用使得热气动弹性问题更为普遍和突出。

热气动弹性问题所表现出的不同现象，均可视为流-热-固多场耦合的不同表现形式［6］。求解高超飞行器流-热-固耦合问题对计算资源的消耗极其巨大。基于Roger［7］三大基本假设的含简化模型耦合分析方法［8］，在早期计算能力有限的情况下使得耦合计算成为可能。但其常用的工程气动力、热计算方法和简化的耦合流程［9］，与实际物理情况往往存在较大偏差［10］，对于复杂流动而言更是如此。随着计算机水平的快速发展，CFD-CTSD 全数值分析方法已成为研究主流。不管在计算策略与精度分析方面［11］，还是试验验证方面［12］，都取得了长足进步。但受制于耦合分析对计算的巨大需求，至今尚未出现完全紧耦合的流-热-固耦合分析［13］，特别是非定常气动力和气动热的计算，面临着显著的效率与精度的矛盾。

统计检验表明：乐视网股价的日收益率平均值为0.000912，中位数为0.0012，标准差为0.042215，说明存在一定程度的离散，偏度系数Skewness小于0，说明收益率时间序列具有一定程度的左偏，而峰度系数Kurtosis大于3，说明时间序列具有明显的尖峰特征；Jarque-Bera统计量相伴概率接近于0，统计结果拒绝原假设，从而表明收益率时间序列不服从正态分布。时间序列图表明：收益率时间序列存在较大波动，并且具有一定的集聚性和爆发性，可能存在ARCH/GARCH现象。[2]

为了解决多场耦合问题中气动力计算面临的效率与精度的矛盾，一种基于结构模态的非定常气动力降阶模型（Reduced Order Model， ROM）得到了发展［5］。这种方法能够快速、准确地预测结构振动带来的非定常气动力响应，并能方便地得到气动弹性分析结果。过去十余年间，气动力降阶模型已应用于操纵面颤振分析［14］、大迎角颤振分析［15］、伺服气弹问题［16］、抖振机理研究与控制［17-18］等实际方面，并且在功能上得到了较大拓展，发展了多种非线性、变马赫数模型［19-24］。然而，上述气动力模型是基于给定振型建立的，在热气动弹性问题中，结构固有频率和振型会随结构温度的变化发生较大改变，这给传统的降阶模型带来了巨大挑战：每当热模态振型发生变化后，就必须重新建立ROM，包括重新调用CFD 求解器获取训练模型所需的广义气动力数据，这极大削弱了气动力降阶方法在计算效率方面的优势。而如果不考虑模态振型的变化，气动弹性分析结果又将出现很大偏差［25-26］。

教师A在反思日志中不断反思课堂教学，其经验性知识和接受性知识在实践过程中通过反思而实现互相转化和促进教师专业发展。其在反思日志中也不断提到之前自己所学过的教学理论，若不进行及时的反思，这些理论无法和自己的教学实践结合起来就无法真正内化为自己的经验性知识，更无法促进自身专业发展。因此，定时、有规律的反思，是教师从实践者向研究者转变的有效途径。

1 计算方法

1.1 时变热模态适用的气动力降阶模型

在高超声速飞行过程中，结构受热会引起热模态振型的实时变化。在气动外形不变的前提下，假设时变热模态振型可以由一组基振型线性叠加表示，即

首先进行定常流场计算，Z=0 m 剖面内流场和壁面压力场结果如图6 和图7 所示。由图6 可见，驻点处产生的第1 道激波在第2 级压缩面附近与拐角产生的第2 道激波相遇，在该区域制造出包含激波边界层干扰、激波干涉的复杂流动结构，并在第2 级压缩面形成了如图7 所示的局部高压区。上述复杂流动下的非定常气动力难以用高效的工程方法准确计算。

Ding[27]等利用适配体组装磁珠纳米结构开发出一种简单、通用、灵敏的电位检测方案，适用于多种目标分子的检测。适配体捕获后磁珠带负电荷，双酚A加入后将适配体竞争下来，暴露的适配体与带正电荷的鱼精蛋白结合，此时磁珠带电荷由负变正，电位变化也会发生明显的变化。随后，同组研究人员又提出一种对2种分子有顺序选择性检测的全固态电位传感器[28]，如图2所示。该传感器利用计时电位法调控阴阳离子的扩散，再利用开路电位法检测实现了2种细菌的选择性检测。该传感器可同时检测大肠埃希菌O157∶H7和金黄色葡萄球菌2个细菌核酸序列，其检出限分别为120和54 fmol·L-1。

式中：Φ= [Φ1，Φ2，…，Φn] ；φ=[φ1，φ2，…，φm] ；γm×n为叠加系数矩阵；n为真实热模态阶数。

式中：L为特征长度；U为流场速度；a为热传导系数。对于高超声速飞行器而言，流场的稳定时间tf远小于结构传热时间tt，即气动热的非定常效应对结构热传导影响很小。因此，采用定常方法获得气动热结果是符合物理过程的。由此，可建立如图2 所示的耦合分析策略。

按可比口径计算，1993年以来贫困县农民人均收入增长快于全国农民平均水平，使贫困县与其他地区农民平均的收入差距缩小。在“八七”扶贫攻坚计划期间，贫困县农民人均纯收入相当于全国平均水平的比值提高了12百分点；2001年至2010年这个比值提高了3百分点；2011年至2017年这个比值提高了10百分点(图1)。

上述基模态振型的构建方法直接关系到后续气动力模型的精度和复杂度，是所提出气动力模型的关键技术。目前，有3 种基模态构建方法：①径向基函数（Radial Basis Function， RBF）方法［27］；②主成分分析（Principal Component Analysis， PCA）方法［28-29］；③直接选择参考结构的模态振型［30］。RBF 方法理论上可以表示任意复杂的形状，但所需基模态数量较多，模型复杂度较高，计算量较大。PCA 方法常用于结构优化设计，所需基振型数量较少，但需要事先在设计变量空间内进行抽样，由于受热结构的时变热模态振型不能在耦合计算之前得到，因此无法事先抽样。对此，本文以未受热结构作为参考结构，采用参考结构的模态振型作为基模态振型。当模态振型的变化仅来自结构加热时，该方法具有较高的精度。

之后，基于基模态振型建立气动力降阶模型：设计m阶基广义位移振动信号ξ*i(t)，其 中i=1，2，…，m，信号带宽需覆盖受热结构可能的前几阶固有频率。启动CFD 求解器，根据ξ*i(t)所给定的位移对物面施加强迫运动d：

利用式（4），将CFD 求解得到的非定常表面压强变换为m阶关于基模态的基广义气动力系数响应fi*(t)：

式中：P为当地物面压强；q为动压。

采集ξ*i(t)和fi*(t)数据，利用系统辨识方法得到基模态下的气动力降阶模型，如ARX （Auto Regressive with eXogenous input）模型。由于该模型的输入和输出都是关于基振型的，无法直接与真实受热结构的热模态进行耦合，因此需要在模型的输入和输出端进行如下变换：

采用1.3 节中的耦合方法计算第2 级压缩面的时变温度分布。分别采用大、中、小3 种不同的时间步长进行气动热-结构传热时域耦合计算，得到如图8 所示的外表面监测点（图4 中标注的相应位置）温度变化历程。可见，3 种时间步长均能获得几乎相同的加热历程，而当时间步长较大时，描述快速温升段的精度较低。对此，算例采用中等大小的耦合时间步长，即时间步长在0～1 s 之间设置为0.1 s，1～20 s 之间设置为1 s，20～30 s 之间设置为2 s。图9 为该时间步长下内、外表面监测点（见图4）的温度变化历程，可见，壁板在10 s 左右基本达到热平衡，外表面监测点温度由200 K 升高到453.64 K，内表面监测点温度由200 K 升高到431.54 K；外表面温度高于内表面约22 K，考虑到壁板厚度仅为2.2 mm，因此厚度方向存在较大温度梯度。0 s 和30 s 时刻的壁板温度分布如图10 所示。可见，由于布置了冷却管，温度场空间分布较为复杂，壁板平面内也存在较大的温度梯度。上述温度梯度导致了热应力的出现，容易使模态振型发生较大变化。

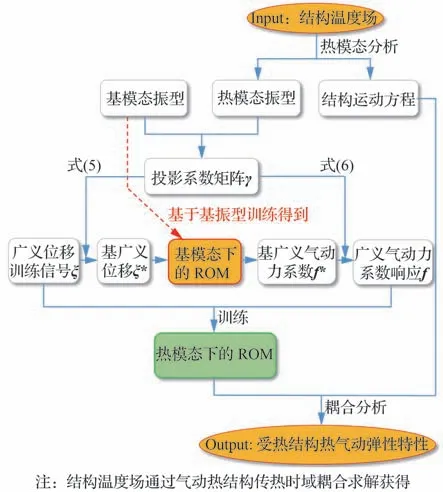
图1 适用于任意结构振型的气动力建模流程Fig. 1 Aerodynamic modeling process of ROM-AMS

可见，无论输入的结构振型如何变化，在基振型上建立的气动力模型都可以重复使用，仅需借助γm×n进行变换，因此，该气动力模型被称为适用于任意振型的气动力降阶模型（ROM suitable for Arbitrary Mode Shapes， ROM-AMS）。

1.2 基于气动力降阶模型的气动弹性分析方法

以ARX 模型为例，气动力模型的一般形

式为

式中：Ai和Bi为待辨识矩阵；na和nb是用户定义的延迟阶数。式（7）可化为连续形式的状态空间方程：

式中：状态量xa(t)包含了历史时刻的ξ、f信息。受热结构运动方程表示为

式中：M为广义质量矩阵；G为广义阻尼矩阵；K为广义刚度矩阵。将式（9）转化为连续形式的状态空间方程：

近年来，该地区先后从战略上提出了打造绿色煤都、创建生态县市、创建国家环保模范城市，打造宜居和谐城市的发展规划。

习近平总书记在江苏考察时强调，国有企业是中国特色社会主义的重要物质基础和政治基础，是中国特色社会主义经济的“顶梁柱”。这一重要指示，明确了新时代国有企业的战略定位。经过40年的改革发展，江苏省属企业已成为全省综合交通运输体系投资建设运营的主力军、江苏地方能源产业和地方金融产业发展的主力军，“走出去”到“一带一路”沿线国家发展的省级排头兵，在全省创新投资中打头阵，同时还承担着全省粮食储备，食用油和盐生产、营销、储备等任务，在农业现代化、南水北调、沿海开发、重大活动保障等方面发挥重要的特定功能。

式中：

耦合式（8）和式（10）得到气动弹性状态方程：

1.3 流-热-固耦合分析方法

热气动弹性问题是一种典型的两域四场［31］流-热-固耦合问题。各物理场求解方式及耦合策略取决于各场所表现出来的物理时间特征［32］。流场流动的特征时间tf和结构场热传导的特征时间tt分别为

式中：T均代指壁面温度场。采用上述方法后，t（i-1）时刻与tr时刻之间的所有时刻的气动热均可采用式（13）快速计算得到。由于预估步长较大，因此在整个飞行过程中数值求解气动热的次数较少。

进入姑苏院子王府形制的大门后，映入眼帘的是一块山水照壁，引人入胜，但是作为景观空间序列伊始，又把院内景观先藏住，含蓄委婉。绕过照壁，视野开阔起来，是“一池三山”的景观格局，把自然山水的形态、风水中的风和气引入这个入口空间中。

图2 流-热-固耦合时间推进分析流程Fig. 2 Flowchart of fluid-thermal-solid coupling time marching analysis

为了降低气动热计算消耗的时间，可根据高超声速边界层理论对气动热计算过程进行简化。当需要计算t（i）时刻气动热时（i代表第i个耦合时间步），可首先基于t（i-1）时刻的热流场结果Qt(i-1)和结构温度场结果Tt(i-1)，以较大的耦合时间步长通过数值方法得到tr时刻的结构温度场Ttr和热流场Qtr，其 中tr时 刻 显 著靠后 于t（i）时 刻。在 巡航状态下，由高超声速边界层理论［33］可知Q∝T，此时有

根据兰州新区的地理、气候及人文特点，色彩规划要考虑多种元素，如：城市环境、人文等，在实践中要做好现代城市的发展规划，形成自然与城市色彩的和谐、统一。根据色彩三层定色控制原则，在掌握好整体的基础上进行合理控制及引导，细分处理，达到个性与和谐相统一的视觉效果。兰州新区位于兰州北部秦王川盆地，年平均气温在6.9℃，年平均降水量约在220mm，但年均蒸发量可多达2000mm左右，有150d左右的无霜期，土壤色彩为黄色，绿色植物比较少。核心区平均海拔约2000米。在整体色彩规划设计过程中，根据兰州新区的地理、气候及人文特点，色彩设计应该受到一些限制。

镜头动作是微视频创作中的一种重要剪辑因素。它指因摄像机位置有目的的移动而带来和构成的镜头的运动变化。它是视频特有的艺术元素，剪辑时要尽可能的充分发挥其独特的功用[1]。专业拍摄中运动性镜头有推、拉、摇、移、跟等多种方式，各有特色和艺术感染力。比如推镜头，指对象位置不动，镜头与画面逐渐靠近，画面外框逐渐缩小，画面内的景物逐渐放大，使观众的视线从整体看到某一布局，引导观众更深刻地感受角色的内心活动，加强情绪气氛的烘托。再比如移镜头，指摄像机横向移动拍摄，可以把行动着的人物和景物交织在一起，形成一种富有流动感的拍摄方式，产生强烈的动感和节奏。

2 算 例

2.1 模型介绍

采用如图3 所示的两级压缩面薄壁模型作为测试算例，原因如下：①两级压缩面是吸气式高超声速巡航飞行器前体部位典型外形，具有一定的代表性；②壁板相比于翼舵部件更容易发生动失稳等热气动弹性问题，该算例原型的第2 级压缩面就在高超声速试验过程中出现了热颤振事故；③相比于其他外形，该算例存在复杂流动，在验证ROM-AMS 方法的建模精度时更有说服力。本节将针对第2 级压缩面壁板，采用ROMAMS 方法开展动热气动弹性稳定性研究。

某品牌细支烟的单支烟重量为0.55g，20支烟重量为11g±0.15g，标准差小于0.014g，要求精度较高。卷烟机由标准烟卷烟机改造而成，原机重量控制系统采用DSP电路板，已经难以满足烟支重量和标准差的要求。

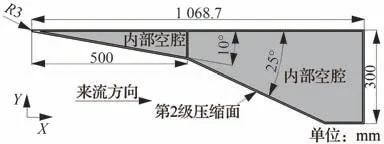
图3 前体部位两级压缩面几何外形及尺寸Fig. 3 Geometric sketch of two-stage compression surface in forebody

图4为第2 级压缩面壁板设计布局，壁板厚度为2.2 mm，模型Z方向宽度为0.5 m。由于受到较为严重的气动加热，为避免结构受热后迅速失效，在壁板内表面（背风面）布置20 条冷却管道，如图4 中阴影区域所示。冷却管覆盖区域设置为200 K 等温边界条件，内表面其余部分设置为绝热边界条件，壁板初始温度设为200 K 均布温度。壁板材料为高温合金，密度为7 800 kg/m3，泊松比为0.3，表面辐射率为0.85。其余材料属性如表1 所示。壁板背风面四周边线为简支边界条件，背压被设置为恰好平衡迎风面压强，使得壁板在气流中不发生静变形。

BIM技术应用改变了传统的工程成本控制管理模式，从单元化的工程施工成本控制迈向多元化发展，以施工材料成本、设备租赁成本及人工费成本等多个成本项目为基础，对成本内容进行核算，并将可能发生的成本管理要素进行预判，提高基础成本核算的科学性，同时将工程施工数据内容进行整合，降低高成本项目资金资源浪费，以此改变传统工程成本控制管理数据信息归纳混乱不堪的实际局面，有条不紊的开展成本控制管理工作，进一步实现成本控制的人机结合，从技术角度及信息化管理角度出发，对工程施工成本控制问题进行解决，实现工程成本控制的合理化应用。

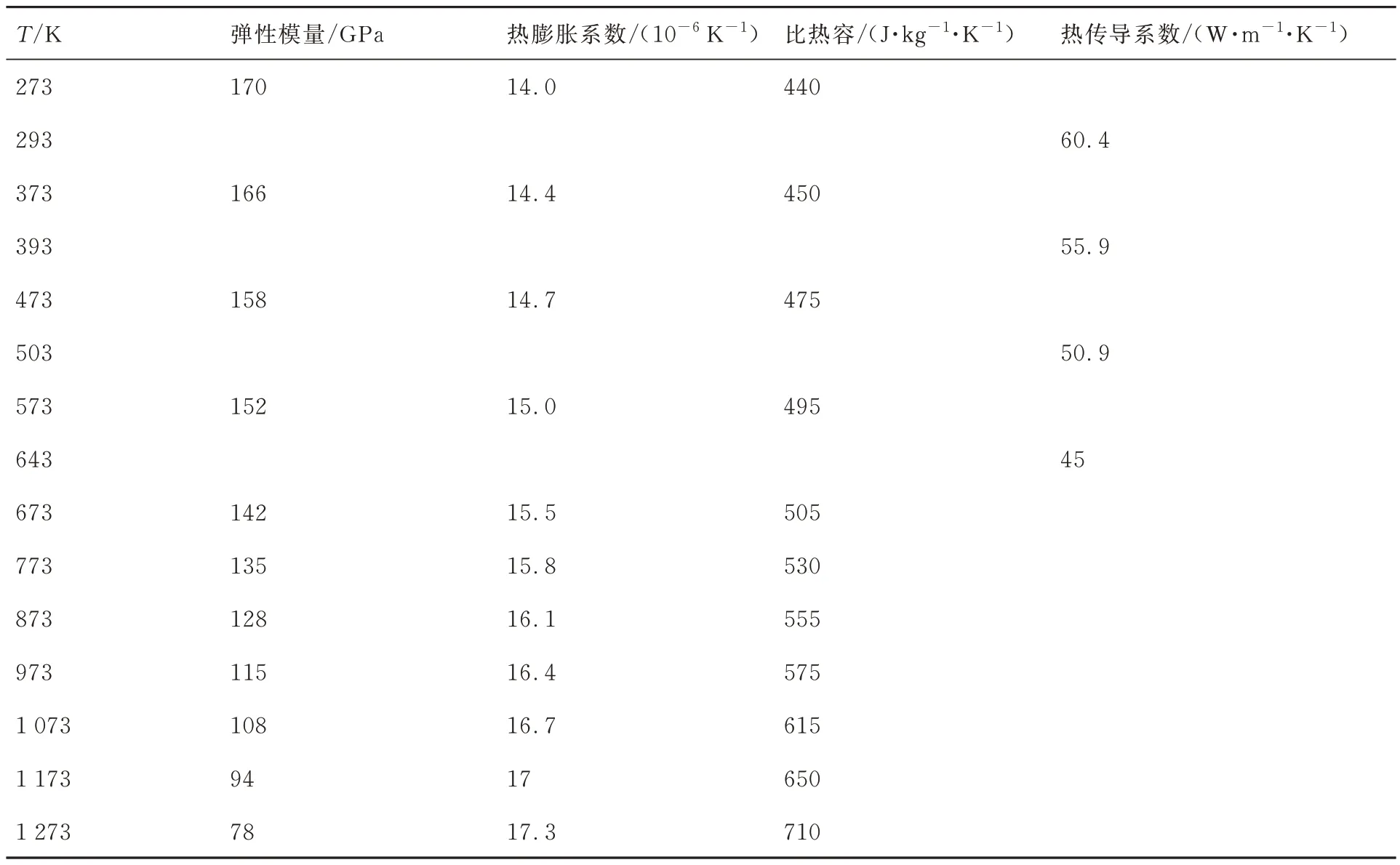
表1 材料随温度变化属性Table 1 Material properties changing with temperature

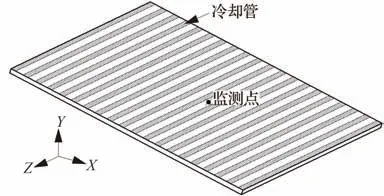
图4 第2 级压缩面冷却管布局Fig. 4 Cooling pipe layout of the second stage compression surface

2.2 计算条件与网格参数

来流马赫数为8.0，飞行高度30 km，飞行时间30 s，来流方向为图5 所示的X轴。为了得到准确的气动力及气动热计算结果，需进行网格无关性验证，以确定合适的首层网格高度。经过网格无关性验证后，首层网格高度确定为4.8×10-6m，对应的网格雷诺数为18.1。图5 为Z=0 m 剖面处的网格切片与局部放大图。

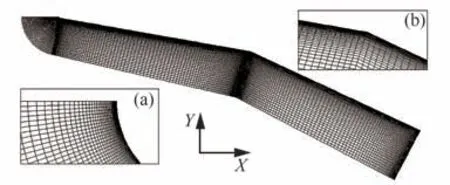
图5 CFD 计算网格及前缘驻点/压缩拐角局部放大图Fig. 5 CFD mesh of flow field including enlarged drawing at leading edge and corner

3 结果与讨论

3.1 初步流场分析

式中：Φj为第j阶热模态振型；φi为第i阶基模态振型；γij为叠加系数；m为基模态振型总数。借助式（2），时变热模态振型Φ可以表示为

针对该问题，本文发展了一种热气动弹性问题适用的气动力降阶建模方法，并以高超声速飞行器前体压缩面为研究对象，采用所发展的气动力模型开展了实际飞行加热过程的时变颤振边界分析，并对比分析了所用方法与传统降阶模型方法的求解效率与精度。

图6 两级压缩面模型流场结构Fig. 6 Flow structure of two-stage compression surface

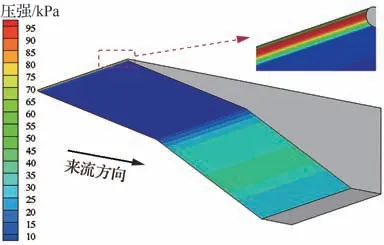
图7 两级压缩面表面压力云图Fig. 7 Pressure contour in two-stage compression surface

3.2 气动热/结构传热耦合分析

式中：ξ和f分别为热模态下的广义位移和广义气动力系数。式（5）将热模态下的广义位移变换为基广义位移，式（6）则将基广义气动力系数变换为热模态下的广义气动力系数，而主导上述变换的正是叠加系数矩阵γm×n。当分析某时刻真实受热结构时，即可利用上述降阶模型，快速得到当前时刻热模态下广义位移信号ξ产生的广义气动力系数响应f，再进一步根据ξ-f数据辨识得到针对当前时刻受热结构的传统气动力模型，最后与结构运动方程耦合进行气动弹性分析，流程如图1所示。

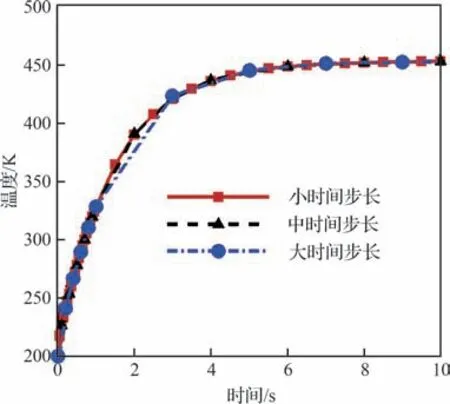
图8 不同时间步长下外表面监测点温度变化历程Fig. 8 Temperature history at outer surface monitoring point with different time step settings

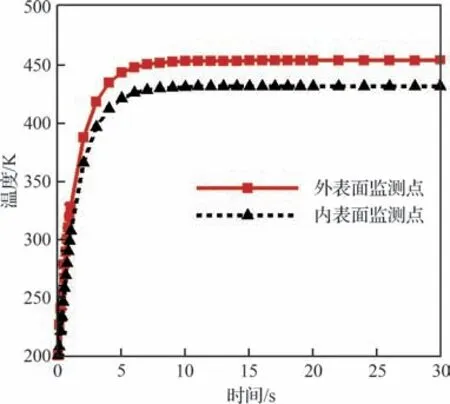
图9 内外表面监测点温度变化历程Fig. 9 Temperature history at inner and outer surface monitoring points

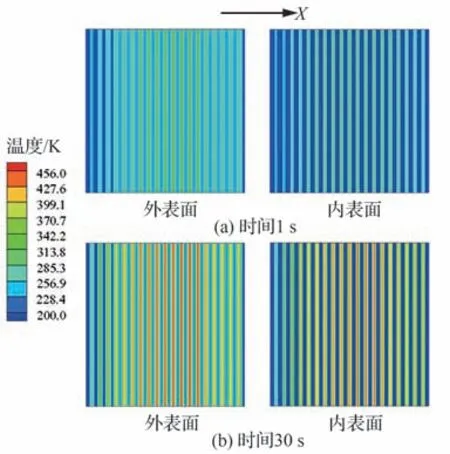
图10 壁板内外表面不同时刻温度场Fig. 10 Temperature fields in inner and outer surface at different time

图11为外表面监测点处热流变化历程，可见，随着壁面温度升高，表面热流逐渐降低，由初始时刻的1.051 MW/m2降低到最终时刻的0.862 MW/m2。为了验证1.3 节提出的气动热估算方法，图12 对比了在30 s 时刻壁面温度下的气动热估算结果和CFD 计算结果（壁板中心线（Z=0 m）处），可见，当壁面温度空间分布较为复杂时，表面热流也体现出相应的空间分布特征，这种分布特性能被气动热估算方法预测得到。相比于CFD 结果，最大的相对预测误差为12.7%。由于研究重点为气动力降阶方法，因此气动热预测方法不做过高的精度要求。

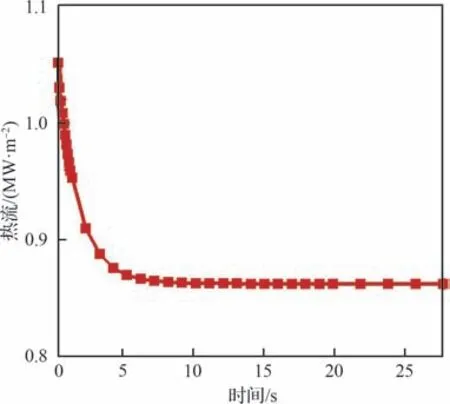
图11 外表面监测点热流变化历程Fig. 11 Heat flux history at outer surface monitoring point

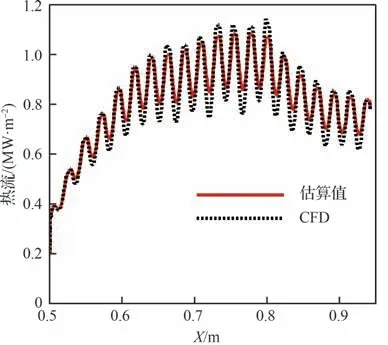
图12 第2 级压缩面区域估计热流与CFD 结果对比Fig. 12 Comparison of heat flux between estimation method and CFD on the second stage compression surface

3.3 时变热模态分析

采用有限元方法得到受热壁板在每个热传导时间步上的前4 阶热模态，用于后续热气动弹性分析。图13 为时变的模态频率，可见模态频率随着加热的持续明显降低，前4 阶模态频率由初始时刻的284.15、407.77、585.64、737.93 Hz降低到最终时刻的80.65、94.13、186.78、340.60 Hz，当接近热平衡时，模态频率趋近于定值。图14 为第1 阶模态振型的变化历程，可以看出，模态振型在结构加热过程中发生了较为明显的变化，其余高阶模态振型变化更为剧烈。此时，如果依然采用传统气动力模型，将无法考虑上述振型的剧烈变化，使得计算结果出现较大偏差，除非在每个时刻基于该时刻模态振型分别建立气动力ROM，而这又会使得计算量提升若干量级，丧失了降阶模型方法的效率优势。对此，后续将建立ROM-AMS 气动力模型以进行非定常气动力计算。

图13 受热壁板时变热模态频率Fig. 13 Time-varying thermal modal frequencies of heated panel

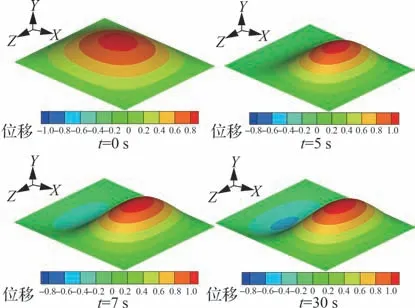
图14 第1 阶热模态振型随时间变化历程Fig. 14 Time-varying graph of the first-order thermal mode shape

3.4 ROM-AMS 气动力降阶模型

将未受热结构（不产生热应力）的前6 阶模态振型作为基模态振型，用于拟合受热结构的前4阶时变热模态振型，基模态振型如图15 所示。为了表征基振型拟合实际振型的精度，定义拟合精度指标（Modal Assurance Criteria， MAC）为

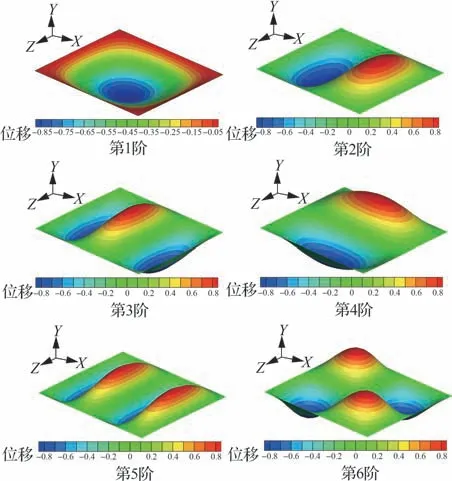
图15 前6 阶基模态振型Fig. 15 The first 6 basis mode shapes

式中：Φ*为基模态拟合出的振型；Φ为对应的真实振型。MAC 值越接近1，表示拟合精度越高。

图16 为基模态拟合各个时刻各阶热模态的MAC 值，可以看到，随着加热的持续，MAC 值逐渐偏离1，但都保持在1 附近，说明基振型拟合精度较高，基模态振型数量足够。图17 为最终时刻（t=30 s）第4 阶真实热模态与拟合模态振型的对比。可以看到，即使是高阶模态振型，基模态也具有较高的拟合精度。

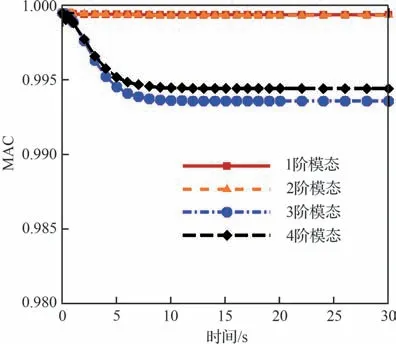
图16 MAC 值随时间变化历程Fig. 16 Time-varying graph of MAC values

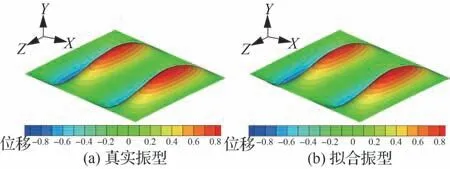
图17 拟合模态振型与真实模态振型对比（第4 阶模态，t=30 s）Fig. 17 Comparison of fitted mode shape and real mode shape （the fourth mode， t=30 s）

采用图18所示的多级信号作为基广义位移训练信号，该信号频域特征如图19 所示，可见，信号的主要频带覆盖了2级压缩面前4阶热模态的频率范围。启动CFD 求解器（RANS 方法，湍流模型kω-SST，时间步长5.0×10-5s）获得基广义气动力响应，再采集上述振动-响应数据辨识得到ROM-AMS，延迟阶数na、nb均 为4。为验证ROM-AMS 的气动力建模精度，针对最终时刻（t=30 s）热结构，给定热模态的广义位移振动信号（图20），分别采用ROM-AMS 方法和非定常CFD 求解器计算上述信号所产生的广义气动力系数响应，结果对比如图21 所示。可以看到，尽管最终时刻热模态振型发生了较大变化，ROM-AMS依然具有很高的建模精度。

图18 训练ROM-AMS 气动力模型所用基广义位移信号Fig. 18 Basis mode vibration signals used for training ROM-AMS aerodynamic model

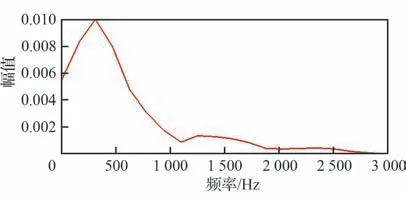
图19 训练信号频域特征Fig. 19 Frequency domain characteristics of training signal

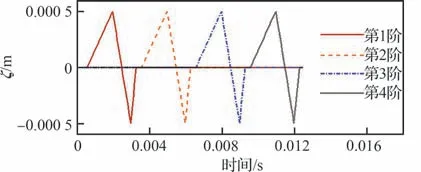
图20 精度测试所用热模态广义位移信号Fig. 20 Generalized displacement signals of thermal modes used for accuracy test

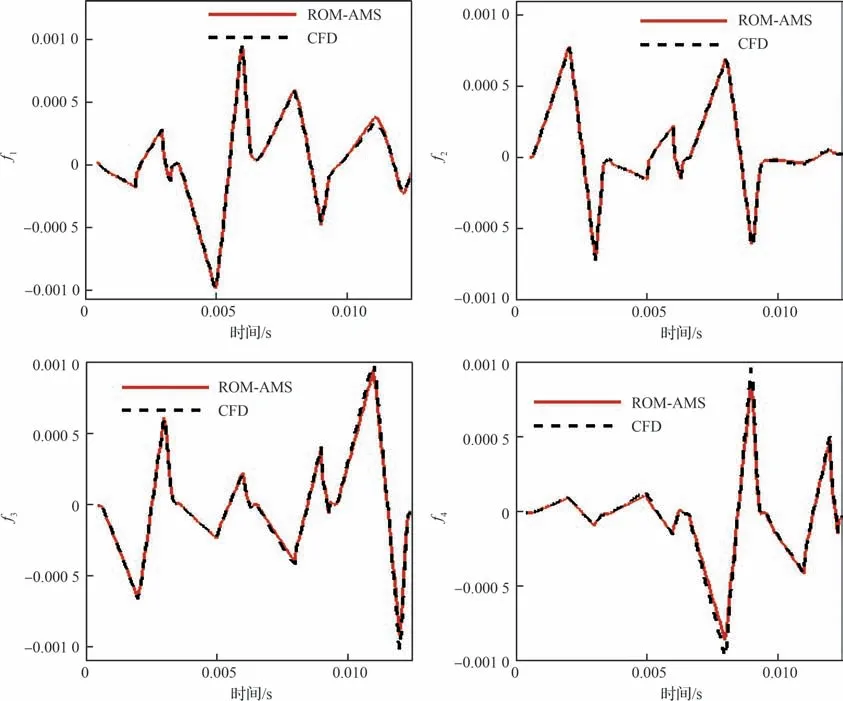
图21 ROM-AMS 方法与CFD 求解非定常气动力结果对比（t=30 s）Fig. 21 Comparison of unsteady aerodynamic results between ROM-AMS and CFD method （t=30 s）

3.5 受热壁板时变颤振边界计算

耦合ROM-AMS 气动力模型与受热结构模态，通过热气动弹性分析得到图22 所示的时变颤振临界动压qf、图23 所示的时变颤振高度边界Hf和图24所示的时变颤振频率ff。可见，随着加热的持续，颤振动压急剧降低，由初始时刻的2.37 MPa降低至最终时刻的0.015 2 MPa；颤振高度边界由初始时刻的5.17 km 升高到38.78 km，这意味着飞行包线会在飞行过程中大幅收窄；颤振频率由初始时刻的472.17 Hz降低至82.98 Hz。

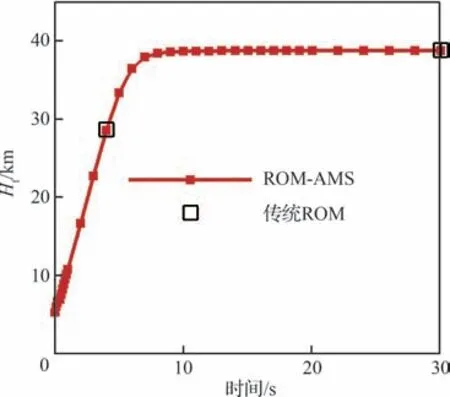
图23 时变颤振高度边界Fig. 23 Flutter altitude boundary history

之后考察ROM-AMS 方法进行热气动弹性分析的精度。由于传统ROM 方法进行颤振分析的精度已进行过较多考核［27-29］，因此将传统ROM得到的结果作为标准解，当ROM-AMS 方法与传统ROM 方法获得结果接近时，即认为ROMAMS 方法精度足够。图22～图24 中给出了在4 s 和30 s 时刻采用传统气动力ROM 方法得到的颤振分析结果。由上述图中可以看出，ROMAMS 方法与传统ROM 方法得到的颤振动压、颤振高度以及颤振频率都非常接近。4 s 和30 s 时刻下不同降阶方法的热气动弹性分析结果对比如表2 和表3 所示。为了进一步考察ROM-AMS方法的准确性，分别采用ROM-AMS 方法和传统ROM 方法计算得到30 s 时刻热结构的v-g图和v-ω图，对比如图25 所示。可见，2 种方法获得的v-g图和v-ω图非常接近，均反映出1、2 阶模态耦合失稳的特征，进一步说明所用方法的准确性。

adc[8]=((float)AdcRegs.RESULT8)*3.0/65520.0+adclo; //读取ADCINB0通道采样结果

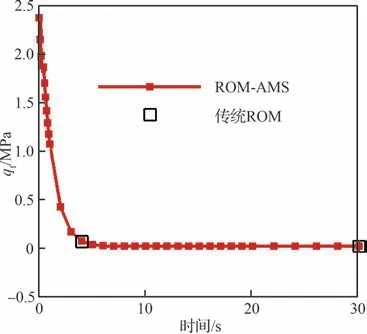
图22 时变颤振动压Fig. 22 Flutter dynamic pressure history

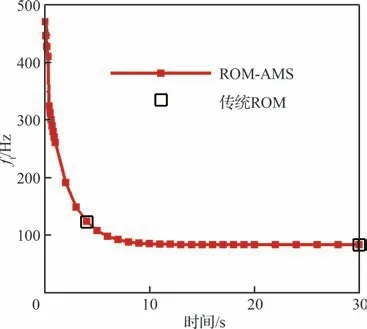
图24 时变颤振频率Fig. 24 Flutter frequency history

表2t=4 s 时刻ROM-AMS 方法与传统ROM 方法热气动弹性结果Table 2 Aerothermoelastic results between ROM-AMS method and traditional ROM method at t = 4 s

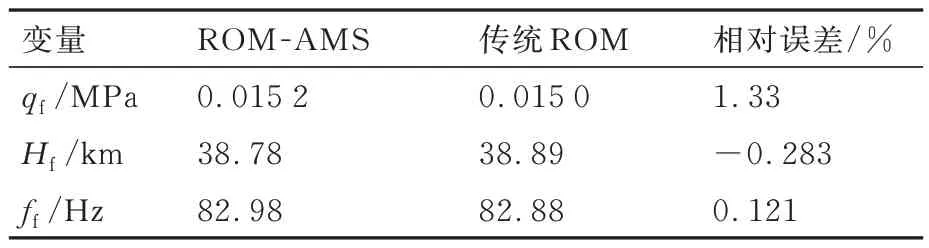
表3t=30 s 时刻ROM-AMS 方法与传统ROM 方法热气动弹性结果Table 3 Aerothermoelastic results between ROM-AMS method and traditional ROM method at t = 30 s

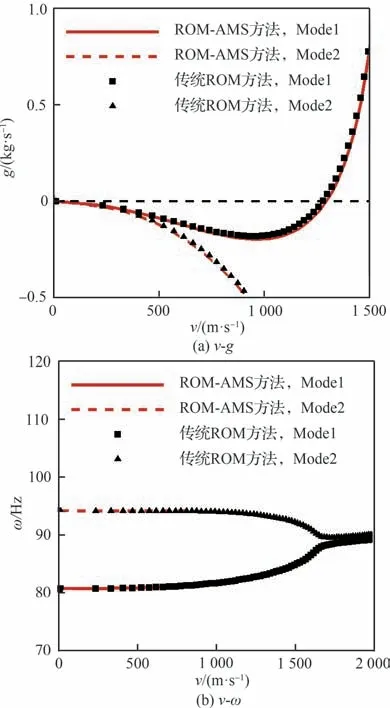
图25 ROM-AMS 方法与传统ROM 方法得到的v-g 和v-ω 图对比Fig. 25 Comparison of v-g and v-ω plots between ROMAMS method and traditional ROM method

最后，对Marques 等的结 论［25］进行验证，证实忽略热模态振型的变化会导致热气动弹性分析结果出现较大偏差。假设在加热过程中不考虑热模态振型随时间的改变，即假定热模态振型始终保持初始时刻的状态，仅仅固有频率发生变化，得到壁板在30 s 时刻的颤振动压为0.042 MPa，相对于正确结果误差达到了180%。该结果表明，采用考虑时变热模态的ROM-AMS方法是十分必要的。

3.6 ROM-AMS 方法效率提升能力

在本算例中，由于共计算了35 个时刻的热颤振边界，因此当采用传统气动力ROM 方法时，需针对每个时刻的热模态重复建立35 次气动力模型，这意味着较为耗时的非定常CFD 求解过程也必须进行35 次；而采用ROM-AMS 方法时，由于气动力模型具有对于变化模态的适应能力，因此CFD 求解过程只需要进行一次，这极大提高了热气动弹性分析效率。在相同的计算环境下（64 核，CPU 主频2.3 GHz），不同气动力降阶方法在热气动弹性分析中的耗时对比如表4 所示。可见，在本算例中，ROM-AMS 方法的效率是传统ROM 方 法 的26.7 倍（表4 中 传 统ROM 方 法的耗时是基于单个时刻热结构分析耗时所进行的合理推断，本文并未真正采用传统ROM 方法计算所有时刻的热颤振特性）。而在真实的长时间飞行中，需要计算更多、更密集时刻的热颤振特性，此时ROM-AMS 方法的效率优势将更为突出，比如当需要在1 000 个时刻上进行热气动弹性分析时，效率提升可达到680 倍以上。

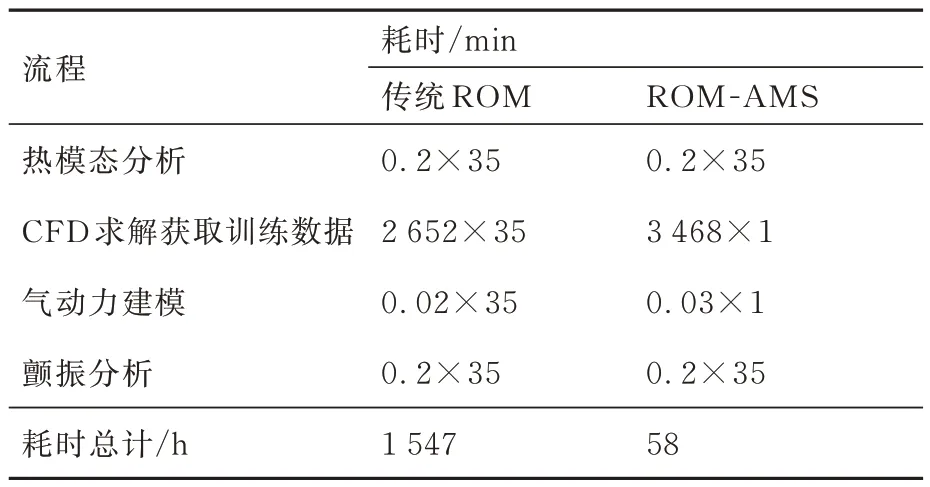
表4 ROM-AMS 方法与传统ROM 方法耗时对比Table 4 Time-consumption comparison between ROMAMS method and traditional ROM method

4 结 论

1）发展的时变热模态适用的气动力建模方法（ROM-AMS）能够适应因结构受热导致的热模态振型的较大变化，采用参考模态方法构建的基模态振型能够准确拟合受热过程中的时变热模态振型。

2）ROM-AMS 方法能够快速预测复杂流动下物面振动产生的非定常气动力响应，模型预测结果与CFD 结果较为接近。

3）当采用气动力降阶模型方法进行热气动弹性分析时，ROM-AMS 方法的效率能达到传统ROM 方法的若干数量级以上，同时能达到与传统ROM 相当的精度。复杂流动下高超声速非定常气动力计算面临的效率与精度的矛盾得到了较大程度的解决。