基于热门度修正因子和置信度的协同过滤算法

刘昊东，王 诚

(南京邮电大学 通信与信息工程学院，江苏 南京 210003)

0 引 言

如今，信息量过载困扰着很多用户，导致无法精确、有效地找到用户感兴趣的信息，还会使用户在获取信息的过程中浪费过多的时间和精力，因此，推荐系统应运而生。目前，推荐系统已经在多个领域得到广泛应用，如教育[1]、电商[2]、医疗[3]、旅游[4]等都有涉及。一般来说，推荐算法主要分为3类，包括基于用户的算法[5]、基于项目的算法[6]以及基于模型的算法[7]，其核心思想分别通过近邻用户、相似项目以及历史数据去挖掘用户感兴趣的内容。

为了使推荐系统的性能得到进一步的提升，许多应用场景也对推荐算法做了相应的改进，从而更好地弥补该算法的一些不足。众所周知，协同过滤算法[8]在推荐领域占据半壁江山，具有高效的性能和较强的解释性。而在实际应用过程中，此算法依旧存在着诸多问题，如拓展性差、冷启动[9]、马太效应、数据稀疏[10]等，影响了推荐系统的性能。为了解决这些问题，许多学者对此做了更近一步的研究。文献[11]为了得到更精确的推荐，考虑时间因素对用户评分的影响和用户之间的非对称影响度，对相似度计算方法做相应的改进。文献[12]提出基于信任的矩阵分解技术，此技术通过建模用户作为受托人和信托人的角色,进而生成信任网络的结构信息，最终将信息源集成到推荐模型中,此方法虽然降低了数据的稀疏性，但是没有考虑热门项目对推荐效果的影响。文献[13]使用标准差反映用户评分值的差异度，将离散系数作为用户评分倾向相似性的判断依据，从而避免项目自身属性对计算相似度的影响。文献[14]主要从完全和非完全冷启动问题进行探讨，首先根据用户与项目之间的联系去构建关系网络，然后通过关系网络去挖掘近邻用户的选取方法，最终融入到协同过滤算法。文献[15]考虑两个用户共同评分的平均差异，以及对项目的偏爱程度，设计了一个可以充分利用用户有限的评分信息的相似度计算模型，从而提高推荐性能。

该文综合考虑了项目热门度和评分矩阵稀疏性两方面因素，提出一种结合热门度修正因子与置信度的协同过滤推荐算法(Popularity Correction Factor and Confidence Collaborative Filtering，PCFCCF)，该算法的优势在于:

(1)通过将热门度修正因子引入到协同过滤算法，可以很有效地削弱热门项目对推荐结果造成的影响，一个项目的热门程度可以通过用户对此项目所发出正向反馈的次数来表示；

(2)通过融入置信度度量函数可以很好地克服用户间共同评分的项目比较稀少的情况；

(3)最终相似度计算公式通过将上述改进的相似度计算公式按照权重进行融合，使得在为用户生成推荐时，既考虑了热门项目对预测评分的影响，又考虑了稀疏度对推荐效果的影响。

1 传统的协同过滤算法

1992年，随着协同过滤算法的提出，它所应用的领域也越来越广泛，此算法的核心思想是通过建立用户行为数据模型进而推荐给用户所感兴趣的项目。推荐算法可以解决如领域、图、关联规则和知识等相关方面的问题，其中在领域这个层次更具有拓展性。推荐算法主要包括三个步骤，首先是用户评分数据模型的建立，其次是寻找与目标用户相似的用户集合，最后根据评分产生相关推荐。

1.1 用户模型的建立

用户可以通过不同的形式向后台反馈相关的数据，因此，第一步需要将用户所反馈的数据进行预处理。建立一个m×n的矩阵S(m,n)来表示用户对项目的行为信息，其中m表示用户的数量，n表示项目的数量，sij表示用户i对项目j的评分值。sij评分值越高，说明用户对此项目的喜爱度越高，用户评分矩阵如式(1)所示：

(1)

1.2 寻找近邻集合

用户间的相似性可以运用如下几个相似度计算公式所求值去度量，从而筛选出相似性较高的用户集合。

1.2.1 余弦相似度

a、b分别代表两个用户的评分向量，计算出来的余弦值与用户之间的相似度成正比，如式(2)所示：

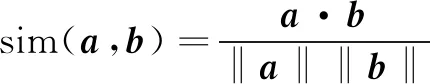
(2)

1.2.2 皮尔逊相似度

(3)

式中，rai、rbi分别为用户a、b对项目i的各自评分，此式取值范围为[-1,1]。

1.2.3 修正余弦相似度

通过对皮尔逊相似度进行改进得到修正余弦相似度，二者的区别是分母中心化的方式不同，如式(4)所示。

(4)

式中，rai、rbi分别为用户a、b对项目i的各自打分，Ia、Ib分别为两位用户各自评分项目的集合；

1.3 产生推荐

通过相似度计算公式获取近邻集合，然后利用式(5)对未评分的项目预测其评分值，最终将预测分数按照从大到小进行排序，取评分较高的前N个项目推荐给用户。

(5)

2 算法改进

随着用户评分的项目越来越多，使得所建立的用户-项目数学模型的评分矩阵的稀疏性也可能会越来越大。虽然一些传统的协同过滤算法已在很多应用场景得到广泛应用，但是通过传统算法去寻找精确度相对较高的近邻集合还是存在着一些壁垒。接下来介绍了传统协同过滤算法存在的一些问题以及对其改进之处。

2.1 评分数据稀疏性的问题

评分数据稀疏性是影响推荐系统性能的问题之一。由于每位用户的喜好不同，他会对不同的项目进行评分，从而得到一个稀疏性较大的评分矩阵，就好比用户A只对一个感兴趣的项目评分，用户B评分项目比较多，而且用户B所评分的项目恰好包括了用户A所评分的项目。通过传统的相似性计算公式计算出二者的相似性会很高，得到的推荐项目也不能很好地反映用户的真实喜好，相应的推荐质量也会很差。考虑到Jaccard函数[17]可以描述集合间相似性这一特性，选取其作为置信度的度量函数，如式(6)所示。

(6)

式中，I(a)、I(b)代表用户a、b各自所评分项目的集合；用户共同评分的项目和评分项目的总和通过两个集合的交集和并集来表示。

将式(6)引入到修正余弦相似度计算公式中，得到改进后的相似度计算公式，如式(7)所示：

(7)

simi1(a,b)在一定程度上缓解了用户间评分矩阵稀疏性较大的问题，使得推荐的项目更满足用户的需求。

2.2 项目热门度差异

随着课外补习班的蓬勃发展，家长们需要在形形色色的课程中做出选择，大多数家长可能为了提升孩子学习成绩选择语数英这类主课，还有一部分家长想为孩子选择一些课外兴趣课程，如美术、音乐等，然而推荐的课程表会出现选择次数较多的语数英这类主课，而这些课程并不能代表家长的意愿。因此，如果运用传统的协同过滤算法会很难探索到目标用户真实的需求。此类问题就是某项目被很多用户评价次数过多而算法未做相应的处理导致的。为了更好地规避这种情况带来的问题，该文通过在皮尔逊相似度计算公式中引入热门度修正因子来抑制热门项目对推荐效果产生的影响，如式(8)所示。

(8)

式中，N(i)表示项目i出现的次数。通过此式可以分析出当N(i)值越大时，相应的p(i)会越小，从而对热门度相对较高的项目起了抑制效果。因此，引入该因子到皮尔逊相似度计算公式中，如式(9)所示：

(9)

式中，p(i)是衡量项目i的热门度修正因子，公式加入该因子后的算法可以弱化此类问题，使推荐的结果更为精确。

2.3 改进相似度计算模型

综合考虑2.1、2.2小节所述，为了更好地减少此类问题对推荐效果的影响，最终将式(7)和式(9)所得到的相似度计算公式按照w，(1-w)的权重进行融合，得到如式(10)所示的最终的相似度计算公式。

Tsim(a,b)=wsimi1(a,b)+(1-w)simi2(a,b)

(10)

其中，w∈[0,1]代表融合两种相似度计算的权重， Tsim(a,b)代表最终用户相似度计算公式，通过该式求出的值越大，说明两位用户之间的相似性也越高，喜好也越接近，使得最终的推荐结果也符合用户的兴趣。

2.4 改进后算法的流程

该文在原有的推荐流程中引入热门度修正因子和置信度系数，不但可以削弱热门产品造成的影响，还可以降低用户评分矩阵的稀疏性对推荐性能的影响。改进后算法的流程如图1所示。

图1 改进后的算法流程

改进后的算法主要包括如下几个步骤：(1)从训练集中提取用户对项目的评分数据进行预处理；(2)构建用户评分矩阵数学模型；(3)按照一定的权重引入热门度修正因子和置信度度量函数去计算用户最终相似度，进而产生近邻集合；(4)将式(10)带入到式(5)预测目标用户对测试集项目的评分prea,i；(5)将评分数值从高到低进行排序，选择前N个项目推荐给目标用户。

上述的步骤3是整个推荐算法的核心部分，与传统协同过滤算法选择邻居用户不同，该算法是融合了热门度修正因子和置信度函数两个参数去研究近邻集合。

2.5 算法分析

文中在计算基于热门度修正因子相似度以及基于置信度相似度时，只是在传统的相似度计算公式乘以相应的因子，并没有做一些复杂的运算，因此，文中的相似度计算方法与传统的相似度计算方法的复杂度都为O(n2)。在没有提升算法复杂度的同时，很好地提高了推荐的性能。

3 实验及结果分析

3.1 实验数据集

该文主要使用MovieLens数据集对改进的算法进行实验研究，其中该数据集主要包括用户信息表、电影名称表以及评分记录表，共包含了1 682部电影，有943个用户对电影做出的100 000条评分记录，本次实验训练集与测试集的配比为7∶3。

3.2 评价标准

该文使用平均绝对误差[18](Mean Absolute Error，MAE)作为评估推荐性能指标之一，其原理是将实验的理论值与实际结果之间的绝对误差的平均值作为度量结果，推荐性能的优劣与MAE值成反比，计算方法如式(11)所示：

(11)

对于测试集T中的用户a和项目i，用户对项目的真实打分用ra,i表示，qa,i为计算所得的预测分数，n表示用户所评分项目的数量。

准确率[19](precision)作为衡量推荐系统性能的重要指标之一，其计算公式如式(12)所示，其精度越高，推荐性能就越好。

(12)

式中，R(u)表示对用户u推荐项目的个数；T(u)表示测试集中用户u喜欢项目的集合。

3.3 实验结果

3.3.1 改进相似度有效性的验证

文中算法在修正余弦相似度计算公式中引入置信度度量函数，以及将热门度修正因子引入到皮尔逊相似度中，因此需要验证这一步骤的有效性。文献[20]将Jaccard函数引入到皮尔逊相似度计算中，将此改进公式用J-PCOS表示其运算的结果，其中PES、ACOS、J-ACOS、P-PES分别表示相似度计算公式(3)、(4)、(7)、(9)的运算结果。选取近邻集合k在[5,50]取值，步长为5，评价指标参考MAE值。对比结果如表1所示，绘制如图2所示。

表1 引入变量后不同相似度计算公式的MAE

图2 引入变量后不同相似度计算公式MAE对比

从图中可以看出，改进的相似度计算公式的MAE都有所降低，因此说明了相似度计算公式中引入这两个因子是有效的。当k<15时，改进公式的MAE下降幅度较大，当k>30时，两个改进公式的效果相差不大，其MAE趋于平稳。并且由图2可知，当k=25时，改进的相似度计算公式在此数据集中计算的MAE取得最小值。

3.3.2 确定权重因子w

由图2可知，在k=25情况下，改变公式(10)中的w的值，在(0,1)区间内选择步长为0.1进行取值，对比不同的w计算出来MAE值，如表2所示，绘制如图3。

表2 不同权重因子(w)对应的MAE

如图3所示，在w取[0.1,0.2]时，最终改进的相似度计算方法的MAE随着w值的增大而减小，之后随着w值的增大，其值也不断增大，因此当w为0.2时，MAE取最小，算法效果最好。

图3 不同权重因子(w)对应的MAE

3.3.3 不同相似度计算方法之间的对比

为了更好地检验改进算法的效果，将改进的算法与文献[11-13]提出的算法以及传统的协同过滤算法(余弦相似度)进行对比实验。结果如图3所示，将w=0.2代入最终的相似度计算公式中，近邻数从5开始，间隔为5直到50为止，分析比较不同的近邻人数与MAE值以及算法准确率之间的关系。如表3所示。

表3 五种算法在MovieLens数据集上的对比

结果如图4所示，此图表示不同近邻个数五种算法MAE值的对比，当邻居数目在不断增加时，改进算法的MAE值先呈现下降趋势，然后逐渐趋于平稳。出现这种情况的原因是随着近邻集合的增加，推荐过程中所参考的用户数目也在增多，因此推荐的精确性也会上升。当邻居数目k为25时，改进算法的MAE取最小值，并且后半段在邻居数目为40、50处与文献[13]算法的MAE值比较接近，虽然其他四种算法的MAE值在随着近邻个数增加时，整体趋势在减小，但是改进算法整体上的MAE值都小于其他四种相似度计算方法。

图4 不同算法之间MAE的比较

图5也证明了该算法显著的改进效果。从图中可以清晰地看出，随着邻居数目的增加，改进算法的准确率也逐渐上升，当邻居数目大于20时其准确率趋于平稳，尽管当近邻数目为30时准确率有所下降，但是改进算法的准确率都高于其他四种算法。

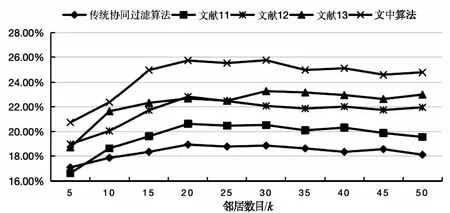
图5 不同算法准确率的对比

4 结束语

主要从两个方面分析传统协同过滤算法在推荐过程中出现的问题，并对用户相似度计算公式进行相应的改进，考虑到由于用户喜好不同，打分项目也不尽相同，评分矩阵稀疏性会偏大，因此引入置信度函数，由于热门项目也会对推荐性能有影响，又引入热门度修正因子。提出了一种融合热门度修正因子和置信度的协同过滤算法，通过控制两种相似度计算公式的权重，得到最终的相似度计算公式。据实验对比分析，改进算法的平均绝对误差(MAE)相应减小，推荐性能有了明显的改善，并且融合权重后的算法的准确率也有所提升，因此该算法的改进效果是显而易见的。但是在对该算法改进的同时，并没有充分考虑到用户的兴趣会伴随着时间的变化而变化这一问题，也就是时间因子对相似度的影响，接下来需要在此方面做进一步研究。