基于热带矩阵密钥交换协议的密码分析
黄华伟,李春华
(1.贵州师范大学 数学科学学院,贵州 贵阳 550001;2.华东交通大学 理学院,江西 南昌 330013)
1 概 述
量子计算机的发展对目前广泛使用的公钥密码体制构成了潜在的威胁,具有抗量子分析的密码体制受到了广泛关注[1]。目前抗量子分析密码体制主要基于交换代数结构,如交换群和交换环[2]。许多学者都希望找到可用于密码学的新的非交换代数结构。例如,Maze提出了基于半群作用问题的公钥加密方案[3]。Baumslag等[4]把格密码研究领域中的带噪声的学习问题推广到一般的代数群上,进而构造出非交换密码方案。Bagheri等[5]提出基于四元数代数的非交换NTRU型密码体制。Climent等[6]提出基于非交换Bergman环的密码体制,但被Zhang破解[7]。
近年来,随着热带代数(Tropical Algebra)的研究逐渐深入,热带代数理论和计算理论研究方面都有很大进展。Grigoriev[8]提出了求解整系数热带齐次线性方程组和整系数热带非齐次线性方程组的多项式时间算法,并证明了求解实系数热带齐次线性方程组是NP-C问题。无论是超定还是未定的实系数热带线性方程组求解都是NP-C问题。Maze等[9]首先提出了基于一类六元单半环的半群作用问题的密码体制,但Steinwandt等[10]利用六元单半环的运算性质破解了该方案。Atani[11]提出了基于因子半环上的半模的密码系统。Durcheva[12]提出基于幂等半环的密码协议。Ahmed等[13]详细分析了它们的缺点并破解了这两个方案。Grigoriev,Shpilrain[14]证明了求解多变量热带非线性多项式方程组是NP问题,并首次使用热带矩阵半环作为平台来构造密码系统,提出了基于热带矩阵的公钥密码体制。由于热带代数只涉及数的加法和比较大小两种运算,因此基于热带代数的密码体制一般效率都非常高。2018年,Kotov等[15]根据整数热带矩阵的代数性质破解了该方案。2019年,Grigoreiv,Shpilrain[16]对原方案进行了改进,提出基于热带矩阵半环的半直积的公钥密码体制。
该文主要研究文献[16]基于热带矩阵半环半直积的密钥交换协议的安全性,提出了一种攻击方法。从协议的公开信息通过简单的二分查找就可获得用户的私钥。结果表明文中的热带代数结构并不适合构建公钥密码体制。
2 整数的热带半环
令Z为整数集合,Z上的热带半环[14,16](tropical semi-ring)为(Z∪{∞},⊕,⊗),其运算为:
(∀x,y∈Z)x⊕y=min{x,y},x⊗y=x+y
(∀x∈Z)∞⊕x=x⊕∞=x, ∞⊗x=x⊗∞=∞
即(Z∪{∞},⊕)与(Z∪{∞},⊗)都是半群,且⊗对⊕满足分配律。
热带半环(Z∪{∞},⊕,⊗)满足以下性质[14,16]:
(1)(Z∪{∞},⊕)是交换半群,∞为单位元;
(2)(Z∪{∞},⊗)是交换半群,无单位元;
(3)(∀x∈Z∪{∞})x⊕x=x。
令Uk为Z∪{∞}上所有的k×k矩阵,即:
Uk={(aij)k×k|aij∈Z∪{∞}}




在U上定义运算∘如下:

引理[16]:令Ω={(M,H)|M,H∈Uk},在Ω上定义运算•如下:




(M1,H1)•(M2,H2)=(M1H2+M2,H1H2)
3 热带矩阵半环半直积的密钥交换协议
用户Alice与用户Bob希望通过协议交换共享密钥。首先,他们选取公开的M,H∈Uk,Alice选取保密的正整数m,Bob选取保密的正整数n。
文献[16]的基于热带矩阵半环半直积的密钥交换协议如下:
(1)Alice计算(M,H)m=(A,Hm),将A发送给Bob;
(2)Bob计算(M,H)n=(B,Hn),将B发送给Alice;
(3)Alice计算KA=BHm+A;Bob计算KB=AHn+B。
因为,
(M,H)m+n=(M,H)m•(M,H)n=
(A,Hm)•(B,Hn) =
(AHn+B,Hm+n)
(M,H)m+n=(M,H)n•(M,H)m=
(B,Hn)•(A,Hm) =
(BHm+A,Hm+n)
所以,Alice与Bob交换了共享密钥K=KA=KB。
(1)Alice计算
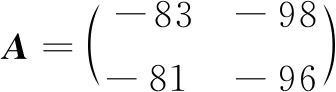
(2)Bob计算

(3)Alice计算
KA=BH13+A=


Bob计算
KB=AH11+B=


该协议的优点是执行速度很快,因为所有的运算都只有整数的加法和比较大小。
4 基于热带矩阵半环半直积的密钥交换协议的密码分析
从协议可知矩阵M,H,A,B都是公开的,正整数m,n是保密的。如果能求出正整数m或n,那么易求出共享密钥。
由整数热带半环的加法定义x⊕y=min{x,y},显然x⊕y≤x,且x⊕y≤y。下面定义一种矩阵的比较大小关系,易知热带矩阵加法也有类似的性质。
定义1:令A=(aij),B=(bij)∈Uk,若∀i,j(1≤i≤k,1≤j≤k)都有aij≤bij,则称矩阵A小于等于矩阵B,记为A≤B。
定义2:令A=(aij),B=(bij)∈Uk,若∀i,j(1≤i≤k,1≤j≤k)都有aij≤bij且存在i,j(1≤i≤k,1≤j≤k)使aij 定理1:令A=(aij),B=(bij)∈Uk,则A+B≤A,且A+B≤B。 由运算定义: (M1,H1)•(M2,H2)=(M1H2+M2,H1H2) 根据命题1,M1H1+M1≤M1,因此(M1,H1)2的第一个分量矩阵小于(M1,H1)的第一个分量矩阵。类似地,(M1,H1)3的第一个分量矩阵小于(M1,H1)2的第一个分量矩阵,……。因此(M1,H1),(M1,H1)2,(M1,H1)3,……。关于第一个分量矩阵是一个递减矩阵序列。 …… 由协议知,(M,H)m=(A,Hm),容易看到,通过简单的二分查找就可以由A求出m。 假设用户A的私钥整数m满足:1≤m≤r,则攻击算法如下: 基于热带矩阵半环半直积的密钥交换协议的攻击算法: 输入:矩阵M,H,A(满足(M,H)m=(A,Hm)); 输出:m (1)令left=1,right=r; (2)若left≤right,执行下面循环 (i)mid=left+(right-left)/2; (ii)计算(M,H)mid=(P,Q) 若P 若A 若P=A,则输出m=mid结束。 例3:用上述算法破解例1。 在Intel(R) Core(TM) i7-5500 CPU @ 2.40 GHz处理器的计算机上运行攻击算法的C程序。 实验一: 按照文献[16]的建议参数:矩阵的阶k=30,矩阵的元属于[-1 000,1 000],在Intel(R) Core(TM) i7-5500 CPU @ 2.40 GHz处理器的计算机上运行攻击算法的C程序,结果见表1和图1。 表1 攻击算法运行时间随指数变化情况 (注:r为指数的上界) 实验二: 指数固定为m=250-1,r=262-1,矩阵元素取自[-1 000,1 000]。在Intel(R) Core(TM) i7-4700MQ CPU @ 2.40 GHz处理器的计算机上运行攻击算法的C程序,结果见表2和图2。 表2 攻击算法运行时间随矩阵阶k变化情况 图2 攻击算法运行时间随矩阵阶k变化情况 固定为r=80,攻击算法的时间复杂度随矩阵阶k增大的情况比较见表3,攻击算法时间复杂度随矩阵阶变化情况见图3。 表3 攻击算法时间复杂度随矩阵阶k变化情况 (注:矩阵的阶为10e,攻击算法时间复杂度O(2d)) 实验三: 指数固定为m=230-1,r=245-1,矩阵的阶固定为k=30。在Intel(R) Core(TM) i7-4700MQ CPU @ 2.40 GHz处理器的计算机上运行攻击算法的C程序,结果见表4和图4。 表4 攻击算法运行时间随矩阵元素取值范围变化情况 (注:矩阵元素取值范围为[-p,p]) 实验三表明,矩阵元素的取值范围对攻击算法的时间复杂度影响不大。 该文分析了Grigoriev和Shpilrain[16]提出的基于热带矩阵半环半直积密钥交换协议的安全性, 在Ω={(M,H)|M,H∈Uk}定义的半直积运算具有部分的保序性,由其乘法定义(M1,H1)•(M2,H2)=(M1H2+M2,H1H2)可知,其第一个矩阵分量小于等于M2,这使得{(M1,H1)n}关于第一个分量矩阵构成了一个单调递减序列。据此,给出了一种二分查找的攻击算法。该算法通过公开信息可以求用户密钥,从而破解了该协议。该攻击算法的比特位运算的计算复杂度为O(2log2r(2k3+5k2)),其中r为指数上界,k为矩阵的阶。实验结果表明,如果协议参数选取自Grigoriev和Shpilrain建议的范围,攻击算法在1分钟之内就能求出私钥。矩阵元素的取值范围对攻击算法的时间复杂度影响不大。对攻击算法有影响的参数是矩阵的阶k和指数取值的上界r,而其中矩阵的阶k的影响又是最主要的。从表3可以看到,除非将矩阵的阶增大到100万阶以上,否则即使增大协议的参数,该攻击仍然有效。因此,热带半环代数结构(Ω,•)并不适合构建安全的密码体制。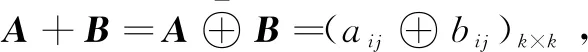



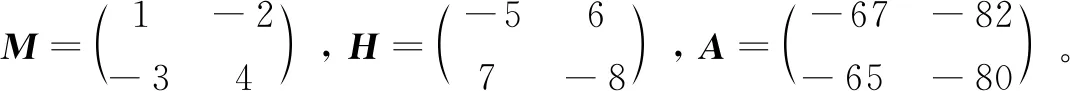


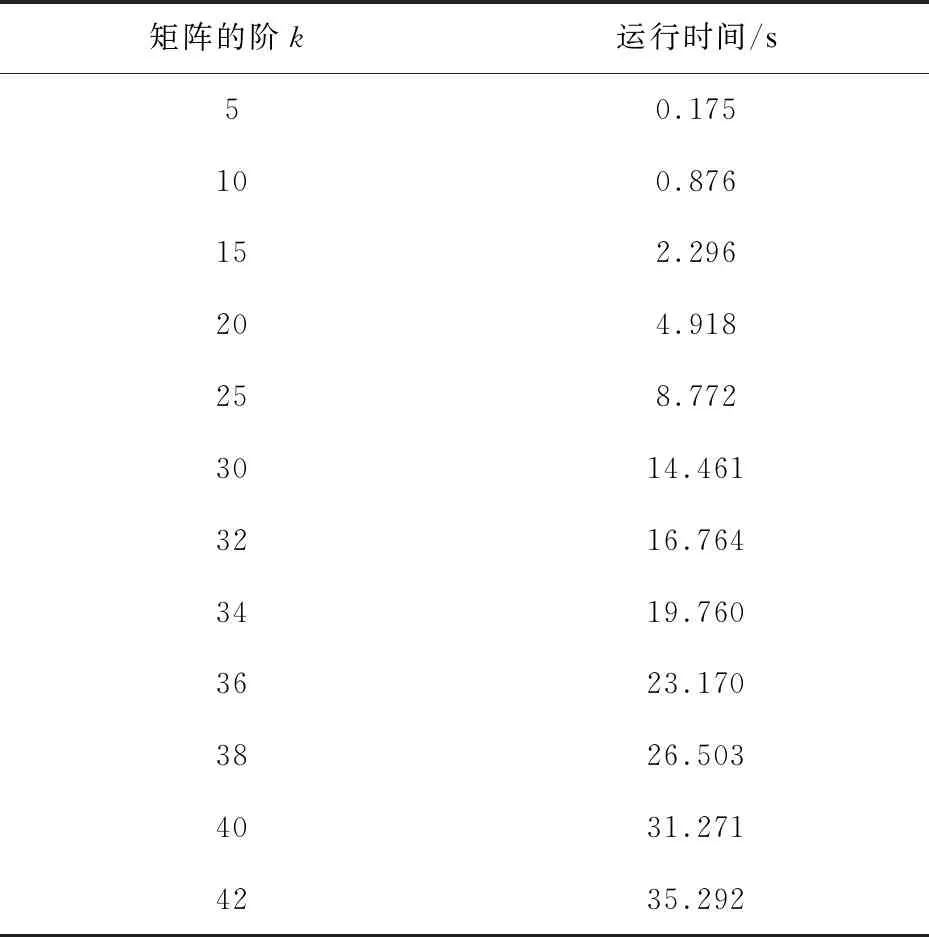





5 结束语

