结合压缩感知和新混沌映射的图像加密方案
周明伟,阚忠良*,蒋东华
(1.黑龙江大学 计算机科学与技术学院,黑龙江 哈尔滨 150080;2.长安大学 信息工程学院,陕西 西安 710064)
0 引 言
随着数字多媒体技术和网络技术的革命性发展,作为信息的一种具体表现形式,数字图像被海量制造、传输与存储。而在信息交换便捷化的当下,数字图像在开放共享的平台上进行传输时容易遭到基于深度神经网络模型的攻击[1],造成隐私泄露,进而引起越来越多的个人用户、企业乃至政府部门对于数据隐私安全的担忧。在此社会背景下,图像密码系统应运而生,以解决在国防军事、医学、工业等诸多领域中的隐私保护问题。
如文献[2]中所述,隐私图像保密技术一般可以分为两大类,一类是图像加密,而另一类则是图像隐写(图像隐藏)。因此可以根据密文图像的视觉纹理是否具有意义来区分它们。图像加密技术指的是在密码流的控制下按照加密规则将具有视觉意义的明文图像转换成类噪声密文图像,与此同时,黑客在没有得到正确密钥的情况下将无法获取密文图像中所携带的敏感信息。
截止到目前,研究人员基于混沌理论[3-4]、DNA编码技术[5]、细胞自动机[6]、压缩感知[7-8]以及马尔可夫模型[9]等提出了许多有效的加密方案。然而,此类图像加密方案均存在一个弊病,即缺乏隐蔽性。当生成的具有统计伪随机特性的密文图像在公用信道中传输或本地化存储时极易被黑客或基于神经网络的各种攻击模型所侦测到,进而遭到诸多类型的攻击。
图像隐写则指的是以一种不可检测的方式将敏感明文图像隐藏到可公开获取的载体图像中,以创建具有视觉安全性的密文图像。也就是说,通过隐藏通信行为的方式来达到传递敏感信息的目的。近些年来,结合传统加密技术与图像隐写技术,如矩阵编码嵌入[10]、离散提升小波变换嵌入[11]、斜变换嵌入[12]和奇异值分解嵌入[13-14]等,以设计出能够实现对明文图像的同步加密和隐写的视觉有意义图像加密算法被相继提出。然而就现有的视觉安全图像加密算法而言,虽然采用基于频域变换的分块嵌入方式来提升算法的鲁棒性,但却以牺牲其不可感知性和压缩性能为代价,进而导致携带秘密数据的数字载密图像容易被基于统计模型或是深度神经网络模型的隐写分析器所发现。
针对上述图像加密算法中所存在的问题,该文利用新设计的离散分数阶Chebyshev混沌映射、二维压缩感知模型以及空域最低有效位嵌入设计出一种高安全性的视觉有意义图像加密算法。首先,在文献[15]的启发下,对经典一维Chebyshev混沌映射进行改进得到其离散分数阶形式的混沌映射。并通过分析其分岔图和李雅普诺夫指数谱验证了该改进型映射具有良好的混沌动力学特性。其次,在明文信息熵的控制下,利用该混沌映射构建出密码流和受控测量矩阵,并用以对明文图像执行二维压缩和加密。最后,再通过无损的空域嵌入方式将秘密图像隐藏到某一可公开获取的载体图像中。实验结果表明:所设计的基于压缩-加密-嵌入框架的图像加密算法不仅能降低密文图像被侦测到和被攻击的概率,同时凭借着明文信息熵和混合扩散策略提升其明文敏感性和密文扩散能力,增强了所提算法在抵御基于明文分析安全攻击模型方面的能力。
1 理论知识
1.1 二维压缩感知模型
在采用传统压缩感知模型处理二维数字图像时,常见做法是先将二维图像堆叠成一维度很大的列向量,然后再对其进行线性测量。但这种处理方式需要占用大量的存储空间和计算资源,因此一些研究者们提出将其扩展到二维正交平面中[16]。
首先,假设一维度为N×N的明文图像P在Ψ域中是稀疏的。则其可以被稀疏表示为:
D=ΨPΨT
(1)
式中,变量Ψ∈RN×N和D∈RN×N分别表示为稀疏表示基矩阵和明文图像P在Ψ域中的系数矩阵,而符号T记为转置操作。
其次,在二维压缩感知模型中,可以通过将图像P的稀疏系数矩阵D线性投影到两个相互正交的测量矩阵Φ1∈RM×N和Φ2∈RM×N上来实现对明文图像的二维压缩,其中符号M与N表示矩阵的行数与列数。此过程的数学表述为:
(2)
式中,Ζ是一个M×M维的测量值矩阵。事实上,矩阵Φ1对明文图像P的行进行操作,而矩阵Φ2则是对其列进行操作。另外,为了能够从矩阵Ζ中精准重构出图像P,需要解决以下优化问题。
(3)
1.2 测量矩阵的构建
在对图像进行二维压缩时,测量矩阵的性能对于解密过程中重建图像的视觉质量有所影响。随机型测量矩阵虽然具有普适性,但其性能难以控制。因此,该文依据混沌映射所具有的伪随机性和统计独立性来构建两个确定型混沌测量矩阵。
具体的构建步骤如下:
步骤1:在给定初始状态和控制参数的情况下,迭代某一维性能优良的混沌映射⎣d·CR·N2」次,生成序列Q。其中变量d和CR表示抽样距离和预设的压缩率,而符号⎣~」表示向负无穷方向取整。
步骤2:对上一步迭代得到的混沌序列Q进行如下处理。
W=1-2·mod(Q(1:d:d·CR·N2),1)
(4)
步骤3:将新生成的伪随机序列W按列重排成二维矩阵,并执行归一化操作,从而得到测量矩阵Φ1。此过程可以由式(5)表述,其中行数M=⎣CR·N」。
(5)
步骤4:根据不同的初始状态重新执行步骤1至步骤3,得到另一个测量矩阵Φ2。
2 所设计的新混沌映射
2.1 新映射的数学定义
针对经典一维Chebyshev混沌映射的分岔图存在空白窗口及稳定吸引子等缺陷,该文通过文献[15]中介绍的方法对其进行改进,得到一维分数阶Chebyshev混沌映射(Fractional-order Chebyshev Chaotic Map,FCCM)。该改进型混沌映射的数学模型如式(6)所示。

acos(x(n-1))),2)
(6)

2.2 性能分析与对比
在x0=0.234 5,v=0.15,h=0.45的情况下,图1给出了所提一维分数阶Chebyshev混沌映射随控制参数μ变化的分岔图。从图中可以看出,相比于原始的一维Chebyshev混沌映射(其分岔图如图2所示),其空白窗口得以消除、混沌空间范围更大以及输出的混沌序列的遍历性更好。另外,由于向原始混沌映射中引入离散步长和分数阶阶数,因此将其应用于图像保密领域可以显著扩展加密算法的密钥空间。

图1 分数阶Chebyshev混沌映射的分岔图

图2 经典Chebyshev混沌映射的分岔图
如果在相空间中非线性系统的轨迹远离其平衡点,则表明该系统不稳定。李雅普诺夫指数(Lyapunov Expone-nt,LE)是一种用于量化描述运动轨迹长期相互排斥和吸引的指标[17]。如果某一系统的LE值为正,则表明其相空间中会出现混沌现象。因此判断一个非线性系统是否为混沌系统,仅需检查其LE值是否大于0。对于一维映射f(x)而言,其李雅普诺夫指数可以通过式(7)计算得到。
(7)
所提一维分数阶Chebyshev混沌映射随控制参数μ变化的LE谱如图3所示。从图中可以看出,在整个取值区间范围内,所设计的非线性映射的LE值均大于0,且随着μ的变化逐渐增大,表明其在整个相空间中均存在混沌行为。除此之外,相比于其他新提出的先进混沌映射而言,其初值敏感性和伪随机性更好。

图3 若干个混沌映射的李雅普诺夫指数谱
3 视觉安全图像加解密算法
所提出的视觉有意义图像加密算法由四个主要步骤组成,即通过分数阶Chebyshev混沌映射生成“一图一密”的密码流,采用压缩感知模型在两个正交方向上对明文图像压缩采样,利用FAN变换置乱和混合扩散策略二次加密明文像素值以及使用LSB嵌入算法将具有统计伪随机性的秘密数据隐藏到非涉密传输介质中。整套加密算法的框架如图4所示。

图4 所提图像加密算法流程
3.1 密码流的生成
鉴于信息熵对消息极度敏感[18],该文采用明文图像的信息熵来构建加密过程中各阶段的密码流以有效抵抗基于选择明文分析的安全攻击模型,其数学定义如式(8)所示。
(8)
式中,符号p(ρi)记为消息ρi的概率。

(9)
3.2 二维压缩阶段
在传统压缩感知模型中,从少量测量值中通过正交匹配追踪、平滑l0范数以及贝叶斯框架等重构算法精准恢复出原始信号的前提是该信号具有可压缩性或在某域中具有稀疏性。但在空域中自然图像普遍不具备此特性,因此通常的做法是采用频域变换将其转换到其他域中进行稀疏表示,从而增加算法的计算和时间复杂度。针对这个问题,该文采用一种对信号稀疏性不敏感的重建算法(2DPG-ED)[19]来提升算法的时间效率。
首先,在二维压缩阶段,第3.1节中所构建的两个受控的正交混沌测量矩阵被用于对明文图像进行二维压缩,并再对压缩后的系数进行线性量化。此阶段可以由式(10)表述。
(10)
式中,函数max和min分别表示取最大值和最小值操作。
3.3 加密阶段
考虑到压缩感知的本质是线性映射[20],其难以抵抗选择明文攻击。因此,所设计的图像加密算法除了采用“一图一密”策略来提高算法的安全性外,还利用FAN变换置乱和混沌扩散策略来掩盖明文图像独有的统计特性并使加密图像具有雪崩效应。具有的操作步骤如下:
FAN变换置乱:FAN变换是Arnold变换的一般形式,其模型如式(11)所示。
(11)
式中,(in-1,jn-1)和(in,jn)表示变换前后的像素坐标,参数t00,t01,t10,t11为该变换的控制参数。根据式(11),对压缩图像P2进行FAN变换置乱,得到矩阵P3。
混合扩散策略:为得到较好的扩散效果,该文结合加模操作和按位异或操作设计出混沌扩散策略,如式(12)所示。
(12)
式中,符号⊗记为按位异或操作,且扩散序列Dx在第3.1节中构建得到。
3.4 嵌入阶段
随着当下深度学习技术的快速发展,基于神经网络的安全攻击模型日益趋于成熟。针对其可以智能地对公用信道中具有类噪声外形的密文图像进行解密分析或恶意破坏等问题,该文利用最低有效位嵌入方式为具有统计伪随机特性的加密数据提供一个非涉密的“视觉标签”以实现对明文图像内容和外形的双重保护。
在嵌入阶段,首先对载体图像L∈N×N的像素值执行缩放操作以防止嵌入秘密图像以后数据溢出,如式(13)所示。
(13)
式中,常数τ取为245。
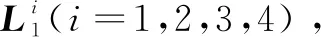
另外,为了提高算法的实用性,最后将明文信息熵的小数位分别提取出来,并在密钥和LSB嵌入算法的控制下,逐个隐藏到密文图像的透明度通道中。
3.5 解密过程
由于所提出的视觉有意义图像加密算法属于对称加密范畴,因此其相应的解密过程为各加密操作的逆过程的集合。另外,为了保证解密密钥的安全性,建议加密方采用非对称加密的方式通过公用信道将密钥传递给授权的解密方。具体的解密步骤如下所示。
步骤1:根据协商一致的非对称加密方式解密出共享密钥并提取出密文图像透明度通道中的明文信息熵,再根据密钥生成规则构建得到受控密码流,如第4.1节描述所示。
步骤2:根据索引序列Ty从隐写图像中逐个提取出秘密图像的各比特部分,随后再进行拼接操作。
步骤3:在逆混合扩散操作策略的控制下,如式(14)所示,从秘密图像P4中重构出矩阵P3,紧接着再执行逆FAN置乱操作。
(14)
步骤4:在对矩阵P2进行逆量化操作之后,再根据文献[19]中介绍的重构算法从测量值矩阵P1中恢复出明文图像,至此,解密过程结束。
4 算法仿真与性能分析
4.1 仿真结果

图5给出了提出的视觉有意义图像加密算法的仿真结果。由此可以看出,明文图像在经过二维压缩加密以后所生成的秘密图像的分辨率是原始的四分之一。同时,其直方图的分布近似均匀分布,表明明文图像所具有的独特统计特性被有效掩盖。其次从视觉上看,最终产生的密文图像与对应的载体图像近似,且重建得到的解密图像与明文图像相差不大。然后,通过峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)和平均结构相似度(Mean Structural Similarity,MSSIM)指标来量化两幅图像之间的视觉差异(它们的数学定义请参考文献[12])。最后经过计算得出密文图像与载体图像之间的PSNR值和MSSIM值分别为39.985 7 dB和0.995 3,而解密图像与明文图像之间的PSNR值和MSSIM值分别为35.028 7 dB和0.910 6。从仿真实验的数值结果可以看出,在不受外界或人为干扰的情况下,所提加密算法具有不错的不可感知性和重建质量。

图5 所提加密方案的仿真结果
4.2 密钥分析


图6 密钥敏感性分析结果
在所设计的图像加密算法中,最主要的密钥是分数阶Chebyshev混沌映射的四组初始控制参数和状态。假设仿真平台的数据精度为10-14,则本算法总的密钥空间为10672,远大于文献[16]提出的最低密钥空间2100。除此之外,构建混沌测量矩阵时的抽样距离d,FAN置乱的参数(t00,t01,t10,t11)以及量化参数均可以作为密钥。综上可知,所提出的视觉有意图像加密算法具有足够的抵抗力以抵御暴力攻击。
4.3 香农信息熵分析
信息熵是反映信息源随机性的最重要指标。它的数学定义如式(8)所示。对具有256位灰度级的数字图像而言,其理论值为8。当横纵向压缩率CR均为0.75时,且将嵌入层移除后,计算出分辨率为512×512的若干明文图像和其相应秘密图像的信息熵,数值结果如表1所示。从实验结果可以看出,秘密图像的信息熵均大于7.99。另外,表2列出不同算法加密Lena512图像后生成的秘密图像的信息熵对比结果。从表中可以得知,相比于文献[13,21-23],所设计的图像加密算法具有更好的密文伪随机性。

表1 明文图像和秘密图像的信息熵

表2 不同算法之间的信息熵对比
4.4 NPCR与UACI分析
像素变化率(Number of Pixels Change Rate,NPCR)和归一化平均变化强度(Unified Average Change Intensity,UACI)[3]常被用来定量评估加密算法抵御差分攻击的能力。它们的数学定义可由式(15)推导出。
(15)
式中,符号I1和I2记作分辨率为W×H的待测试图像。
实验选取四幅维度为512×512的明文图像(Lena,Baboon,Boat和Peppers)进行分析,并且仅将它们的第一个像素点的值加一或减一以生成相应的测试用图。最后在移除嵌入阶段的情况下根据式(15)计算得到不同明文图像所对应的NPCR和UACI值,如表3所示。

表3 不同算法之间的NPCR和UACI值对比 %
从实验结果可以看出,明文图像的微小变换必将导致其所对应秘密图像发生巨大的改变,同时也说明所提算法具有足够抵御差分攻击的能力。另外,通过对比其他加密算法的实验数据可以得知,该算法的抗差分性能可以与文献[16]的媲美,且优于文献[13]。
4.5 不可感知性分析
就具有视觉安全性的图像加密算法而言,其密文图像与相应载体图像之间的视觉差异越小,则所提算法的不可感知性越强,则秘密图像被侦测到的概率越小。接下来,采用不同的加密算法分别加密若干个分辨率为512×512的明文图像并随机地嵌入到非涉密信息传输介质(载体图像)中。随后计算出不同组实验的PSNR值和MSSIM值,结果如表4所示。

表4 不可感知性分析的实验结果
从得到的实验数据来看,相比于文献[13]所提出的基于变换域有损嵌入方法的视觉有意义图像加密算法,该文所设计的加密算法能明显得到9 dB左右的峰值信噪比提升。总的来说,采用最低有效位替换的嵌入方式可以有效提高所提加密算法的不可感知性。
4.6 鲁棒性分析
由于目前几乎所有的公用传输信道都是具有噪声的信道,因此密文图像须具有较强抗噪声或数据丢失的能力。也就是说当密文图像被噪声弄模糊或存在数据丢失之后,通过解密算法仍然可以从中恢复出原始图像的大部分纹理信息。另外,以分辨率为512×512的“Lena”图像作为明文图像,“Baboon”图像用作载体图像。首先,对明文图像进行加密并随机地嵌入到载体图像中的各个区域。然后,对具有视觉安全性的密文图像进行不同百分比强度的数据裁剪(Data Cropping,DC)、椒盐噪声(Salt & Pepper Noise,SPN)和斑点噪声(Speckle Noise,SN)攻击。最后,图 7给出了使用正确密钥解密受攻击后的密文图像的实验结果。可以从图中看到,重建后的图像在视觉上仍然是有意义且可读的。这表明即使密文图像的数据发生一定程度的变化,所提出的解密算法仍然可以恢复出原始明文图像中的大部分信息。因此,所提出的算法对噪声污染和裁剪攻击具有一定的鲁棒性。

图7 鲁棒性分析的实验结果
4.7 时间复杂度分析

表5列出不同算法加密分辨率为512×512的“Lena”明文图像时各个阶段所消耗的时间。从得到的实验数值结果可以看出,所提加密算法的加密速度低于文献[13]中所介绍的算法,但高于文献[25]所提出的算法。因此,建议将大规模的明文图像进行分块处理之后再进行压缩加密和LSB嵌入以提高该算法的加密效率。一方面,可以通过降低图像块的维度来减少分数阶Chebyshev混沌映射的迭代次数。另一方面,图像块维度的降低可以大大节约重建过程中求解凸优化过程的耗时。
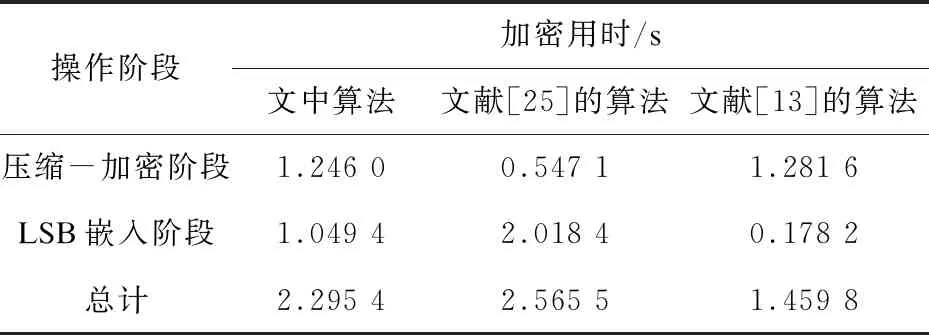
表5 不同算法的加密用时对比结果
5 结束语
首先提出一种新的分数阶形式的Chebyshev混沌映射,并通过分岔图和李雅普诺夫指数对其性能进行评估。实验结果表明,与新提出的其他一维混沌映射相比,所设计的FCCM映射具有更大的混沌范围和更复杂的混沌性能。另外,在此基础上,结合二维压缩感知模型和LSB嵌入提出了一种基于压缩-加密-嵌入架构的视觉安全图像加密算法。该方案中,在分数阶混沌映射的控制下,通过测量矩阵、FAN变换置乱、混沌扩散策略以及最低有效位替换嵌入完成对明文图像的双重加密。最后通过从密钥、抗差分攻击、不可感知性和加密效率等方面进行实验仿真和分析,证实所提算法在保证足够安全之外,还降低了密文图像遭到攻击的可能性。在后续的研究中,将对多幅隐私图像的安全通信进行研究以提升现有保密方案的传输效率。

