高山峡谷桥址处风场特性的大涡模拟研究

严磊，李妍，何旭辉，邹云峰

(1.中南大学 土木工程学院，湖南 长沙，410075；2.高速铁路建造技术国家工程研究中心，湖南 长沙，410075；3.轨道交通工程结构防灾减灾湖南省重点实验室，湖南 长沙，410075)

随着我国基础设施的快速发展，跨越高山峡谷的桥梁越来越多。高山峡谷桥梁距离谷底的高度大，两山之间的桥跨大，导致桥梁结构刚度小，风荷载成为桥梁结构的控制荷载之一。高山峡谷风场受峡谷加速效应、山脉遮挡效应以及越山风等作用的影响，风场特性复杂[1]。例如，受狭管效应的影响，峡谷内部的气流加速形成高风速的“峡谷风”[2]；而受到山脉遮挡时，峡谷内风速通常不再符合幂函数律[3-5]，在有些风向角下还会出现“S”形平均风速剖面[6]，峡谷内平均风速低而湍流度高，湍流度明显大于规范推荐值[7]。ZHANG等[8]对雅安—康定高速公路大渡河大桥桥址周围9 km 范围内的地形风场进行了风洞试验，认为主梁设计基准高度处湍流度受风向角的影响大；当上流有地形遮挡时，湍流度远大于规范推荐值，且顺风向、横风向和垂直向湍流度三者之间比值与规范推荐比值也有较大差异。LI等[9]对龙江大桥桥址处风场特性进行了研究，认为在相同风向角来流下，不同桥塔处的湍流度受局部地形影响，也会呈现出较大的差异。所以，高山峡谷风场具有复杂多变、湍流特性显著等特点，不能简单地通过规范[10]确定桥梁设计基准风速和湍流度等设计风参数，需开展高山峡谷风场特性的精细化研究。

当前研究高山峡谷风场特性的手段主要分为现场实测、风洞试验和数值模拟。现场实测可以对桥址的三维风速进行长期测量，但实测成本较高，且只能获取少数离散点位置的风速样本。风洞试验成本较低，试验时间较短，是常用的准确获取风场特性的方法，但地形模型尺寸常受风洞尺度的限制。近年来，随着计算效率的提高，采用数值模拟获取高山峡谷风场特性的研究逐渐增多。我国现行规范[10]认为桥梁结构或构件的相关参数及抗风性能可通过虚拟风洞试验(即数值模拟)进行获取和检验，但数值模拟的准确性是目前最受关注的问题。于舰涵等[11]采用雷诺时均湍流模型模拟了以坝陵河大桥桥址为中心8 km 边长的正方形区域内的风场特性，获得了与地形模型风洞试验基本吻合的模拟结果。NAKAJIMA 等[12]采用风洞试验和数值模拟对高山峡谷的高湍流风场进行对比研究，发现大涡模拟获得的湍流特征较雷诺时均模型更接近试验结果。BECHMANN等[13]分别采用雷诺时均模型和大涡模拟研究了Askervein山的风场特性并与实测结果进行对比，发现这2种湍流模型均能准确预测平均风速和山脉迎风侧的湍流动能(与脉动风速标准差的平方成正比)，但对于尾流区的湍流动能，大涡模拟具有更高的精度。为更加准确地模拟高山峡谷风场的湍流特性，本文采用大涡模拟对川藏线迫龙沟大桥桥址的风场特性进行模拟研究。

另一方面，高山峡谷的大气边界层厚度较大，合适的入口湍流可以促进稳定大气边界层的形成[14]，从而减小数值模拟所需截取的地形范围。目前，生成大涡模拟入口来流的方法有预前模拟法和直接合成法两大类。预前模拟法生成的风速满足纳维-斯托克斯方程，但其计算量大。目前，研究人员常采用直接合成法对入口湍流进行模拟。例如，REN等[15]采用谱合成法，以Simiu谱和幂函数律风剖面为目标，通过函数生成了与Simiu谱吻合效果较好的风速时程，并将其直接赋予山区地形的入口边界。沈炼等[16]根据观测站风速样本等效而来的风谱生成了入口湍流，经对比认为考虑入口湍流的模拟结果更符合当地实际风场特征。本文采用谐波合成法直接生成大气边界层来流以研究入口来流类型对高山峡谷风场特性的影响。

1 数值模拟分析

1.1 地形概况

川藏线迫龙沟大桥位于西藏林芝地区，主跨430 m，横跨“U 型”峡谷，与河谷走向呈90°夹角。迫龙沟大桥桥址周围20 km范围内的地形如图1(a)所示。该地形范围内最高海拔为5 440 m，最低海拔为1 749 m，峡谷内海拔变化较大，地形复杂。

1.2 风洞试验布置

当采用数值模拟手段研究高山峡谷风场特性时，其准确性一直备受关注。本文通过与地形模型风洞试验结果进行对比分析，验证大涡模拟的准确性和有效性。风洞试验的地形模型及测试设备如图1(b)所示。该地形模型试验在同济大学的TJ-3 风洞进行[17]，风洞试验段长14 m，宽15 m，高2 m。地形模型以主跨跨中为中心，截取直径在10 km 范围内的地形，在10 km 范围以外设置直线斜坡补偿段实现地形表面至风洞地面的过渡，地形模型缩尺比为1∶2 200，地形模型直径约为5.5 m。地形模型范围内最高海拔为4 160 m，最低海拔为 2 000 m，高差达2 160 m。试验来流采用均匀流，平均风速为12.5 m/s。采用眼镜蛇探头测量2个桥塔处的平均风速和脉动风速标准差剖面，塔顶以下每隔0.5 cm布置1个监测点，塔顶以上每隔5 cm布置1个监测点。

图1 迫龙沟大桥桥址周围地形图及风洞试验中的地形模型Fig.1 Location of Polonggou Bridge within surrounding topography and general layout of terrain model in wind tunnel

1.3 数值模拟网格及相关参数

为与地形模型风洞试验结果进行对比，数值模拟的计算域尺寸与风洞尺寸保持一致，计算域布置如图2(a)所示，计算域高2 m，宽15 m，长14 m。为使地形模型的尾流充分发展，将地形模型置于计算域中心并加长尾流区进行无关性检验，结果表明当前设置下加长尾流区对计算结果影响很小。然后，分别模拟计算域高度为2.25，2.50，2.75，3.00，4.00，5.00 和6.00 m 时的桥址风场，发现计算域高度对桥址风场有一定影响，但当计算域高度为2.00 m 时，模拟结果与风洞试验结果误差最小。因此，仍采用计算域高度为2.00 m 的设置。在软件ICEM 中使用Swept 块对计算域进行网格划分，如图2(b)所示。地形模型表面附近采用六面体网格，最小和最大水平网格尺寸分别为0.01 m和0.03 m，其他区域采用棱柱体网格，最大水平网格尺寸为0.23 m。

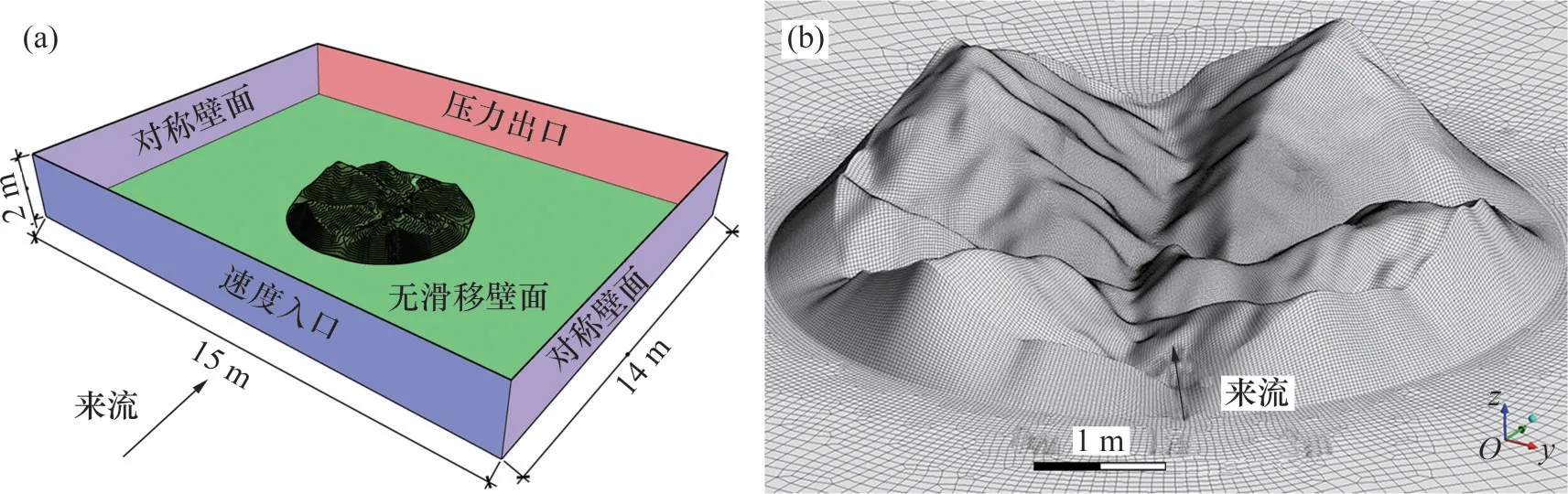
图2 数值模拟计算域布置及网格划分Fig.2 Computation domain for numerical simulation and grid arrangement of terrain surface

为保证后续迭代计算中的收敛性，第一层网格高度取0.00 045 m，沿高度方向网格尺寸的增长率为1.05，地形模型表面大部分区域的y+不超过3，山脊及山峰位置网格扭曲度较大，y+不超过10，网格总数量约为500 万个。为验证网格无关性，分别将网格尺寸设置为上述尺寸(记为中等尺寸)的120%和80%进行网格划分，分别得到粗糙和精细网格。粗糙、精细网格的网格总数量分别约为350万和916万个。采用粗糙、中等和精细网格的数值模拟结果与风洞试验各监测点平均风速的绝对误差平均值分别为2.03，1.62 和1.64 m/s。因中等和精细网格的模拟绝对误差较小且接近，故认为中等网格满足网格无关性的要求。数值模型的计算时间步长设置为0.001 s，计算4 000步后开始监测数据，共记录6 000步。为验证时间无关性，分别将计算时间步长减小一半(即0.0 005 s)和监测数据增大1 倍(即12 000 步)，数值模拟结果与风洞试验各监测点平均风速和脉动风速标准差的绝对误差平均值分别不超过0.18 m/s 和0.16 m/s，故认为数值模拟结果基本不受计算时间步长和监测总时长影响，本文数值模拟的时间无关性亦满足要求。

1.4 边界条件

数值模拟中的入口边界设置为速度入口，通过用户自定义函数加载每个时间步的速度；出口边界设置为压力出口；两侧边界设置为对称壁面；顶面、地面及地形模型表面边界设置为无滑移壁面。空间及时间差分格式分别设置为中心差分和二阶隐式，压力速度耦合方法为SIMPLE 法。2 种入口来流分别为12.5 m/s 的均匀来场(与风洞试验一致)和B 类标准地貌的边界层来流。根据地形模型风洞实验结果[17]，当风向角为垂直于桥轴线的西北风(335.2°)时，迫龙沟大桥主梁高度处的来流风速大，因此，本文选用该风向角进行数值模拟研究。在15 m×2 m 的入口边界上布置600 个速度输入点，如图3(a)所示。然后，在MATLAB 中采用谐波合成法生成所有速度输入点处的离散风速时程[18]。地形模型范围内的平均海拔约为3 300 m，地形模型底面的海拔为2 000 m，规范[10]中标准B类地貌的梯度风高度为350 m，本文假设边界层来流的入口边界梯度风高度δ0为

缩尺后对应的风洞内梯度风高度δ=0.75 m，梯度风速取12.5 m/s，地表粗糙度系数α0=0.16，目标功率谱为von Kármán 谱，横风向各脉动风速的相关性衰减系数采用Cuy=Cvy=Cwy=7，垂直向各脉动风速的相关性衰减系数采用Cuz=Cvz=Cwz=10。通过FLUENT 的用户自定义函数功能读取离散风速时程并赋值到入口边界对应的速度输入点上。假设入口边界的平均风速和脉动风速标准差剖面如图3(b)所示。

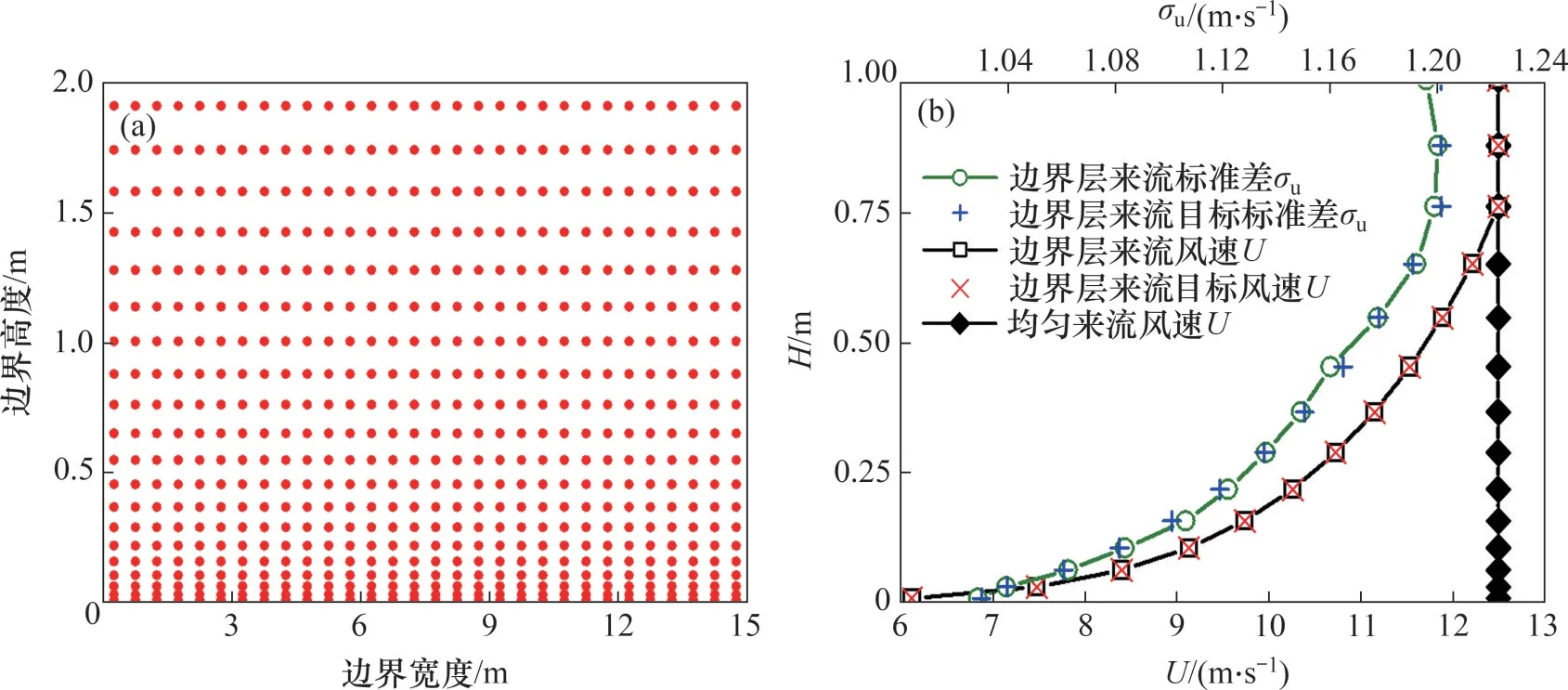
图3 入口边界上的速度输入点位置和平均风速及脉动风速标准差剖面Fig.3 Locations of velocity input points on inlet boundary and corresponding mean wind velocity and standard deviation profiles of fluctuating wind speed

2 结果比较及分析

2.1 数值模拟准确性验证

大涡模拟和风洞试验得到的不同高度处平均风速U和顺风向脉动风速标准差σu如图4所示。从图4可见：两桥塔位置的平均风速随高度增加而增大，但受高山峡谷的影响，平均风速剖面并不严格符合幂函数律。拉萨侧桥塔位置的顺风向脉动风速标准差σu在近壁面随高度增加而减小，当高度达到0.05 m后，σu开始随高度增加而增大，当高度超过0.37 m时，σu却随高度增加而迅速减小，成都侧桥塔位置的σu变化规律类似。本文假设塔顶以上2个连续监测点之间的平均风速相对误差不超过1.5%时的风速为梯度风速，相应的高度为梯度风高度。拉萨侧桥塔处风洞试验和大涡模拟所得的梯度风高度均为0.75 m，成都侧桥塔风洞试验和大涡模拟所得梯度风高度分别为0.80 m 和0.75 m，大于规范D 类地貌推荐的梯度风高度(缩尺后为0.205 m)，约为周围地形最大高差的0.8倍。

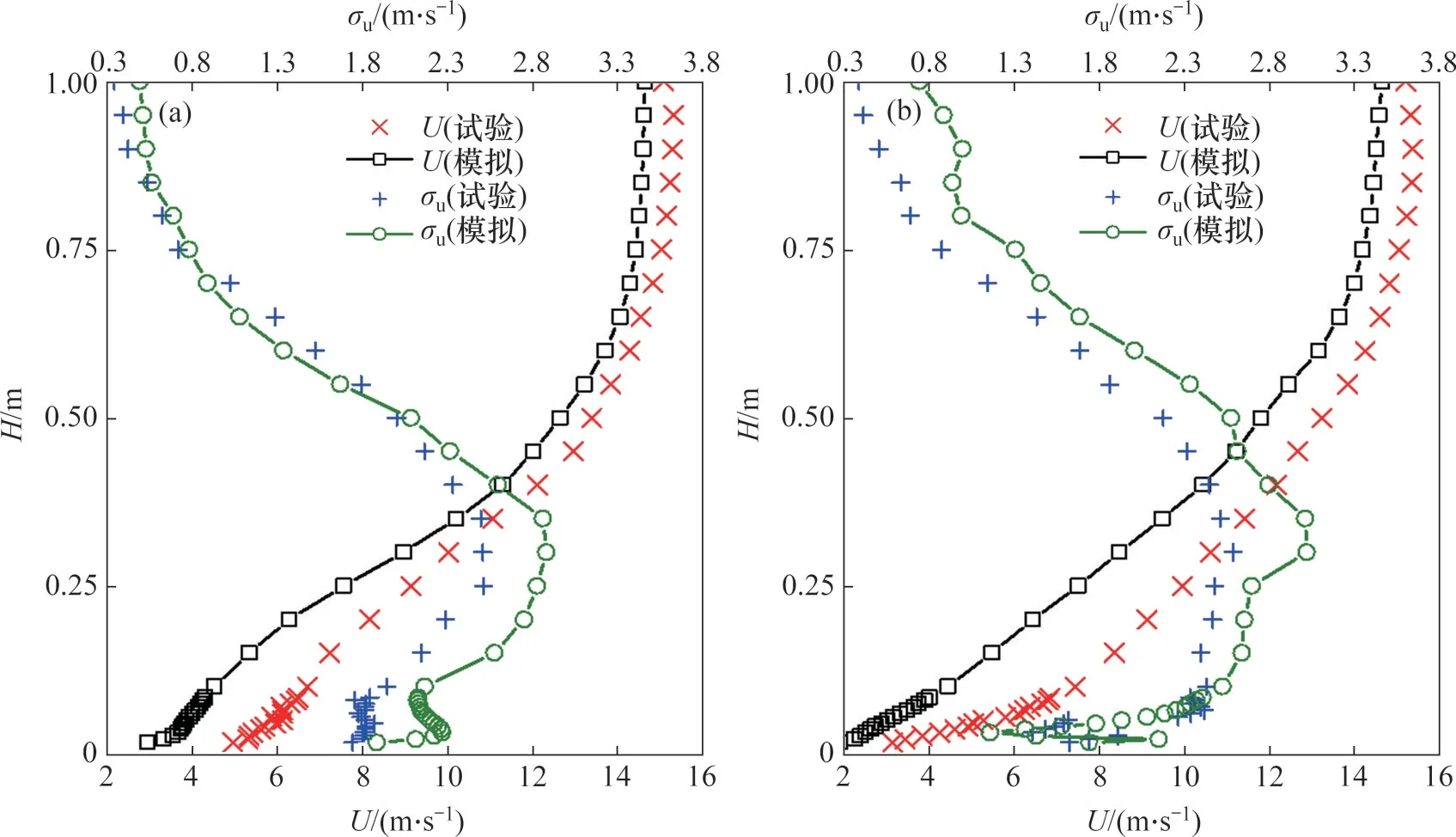
图4 拉萨及成都侧桥塔数值模拟与风洞试验平均风速和顺风向脉动风速标准差对比Fig.4 Comparison of U and σu between numerical simulation and experiment at two bridge towers

采用相关性系数对平均风速和脉动风速标准差随高度变化趋势的相似程度进行量化分析，相关性系数r定义为

其中：X为不同高度的试验平均风速或脉动风速标准差；Y为相应的不同高度的数值模拟结果；Cov(X,Y)为X与Y的协方差；Ⅴar[X]为X的方差；Ⅴar[Y]为Y的方差。

大涡模拟获得的平均风速与风洞试验结果变化趋势较相似，拉萨侧和成都侧桥塔的平均风速相关性系数分别为0.999 和0.992。当高度为0.5 m以上时，大涡模拟与风洞试验的相对误差很小，拉萨侧桥塔处相对误差小于5%，成都侧桥塔处相对误差小于10%。大涡模拟获取的平均风速较风洞试验结果整体偏小，平均绝对误差分别为-1.41 m/s和-1.84 m/s，误差较小。对于顺风向脉动风速标准差σu来说，大涡模拟结果和风洞试验结果的相关性系数分别为0.975和0.934，略低于平均风速的相关性系数，但两者变化趋势也较吻合。特别地，拉萨侧桥塔0.45 m 高度以上的大涡模拟结果和风洞试验结果的误差非常小，平均绝对误差不超过0.15 m/s。

两桥塔位置的横风向脉动风速标准差σv和垂直向脉动风速标准差σw如图5所示。从图5 可见：拉萨侧桥塔的脉动风速标准差随高度增加先增大后减小，σv在高度为0.25 m时达到最大值，σw在高度为0.35 m 时达到最大值；成都侧桥塔的脉动风速标准差在近壁面位置存在突变，在0.1～0.3 m 范围内随高度增加而增大，然后，随高度增加而减小。受上流地形尾流的影响，两桥塔不同高度处的σv和σw较大，σu∶σw小于规范推荐的1∶0.50，而大部分高度处的σu∶σw达到了1∶0.80 左右，在成都侧桥塔0.75 m高度达到最小值1∶1.17。成都侧桥塔的σv与σu相当，在高度0.75 m 处的σu∶σv约为1∶1.12；大涡模拟对拉萨侧桥塔不同高度处的σv和σw预测较准确，与风洞试验结果的相关性系数分别为0.976和0.847，而成都侧桥塔的相应相关性系数分别为0.890和0.827，误差稍大。

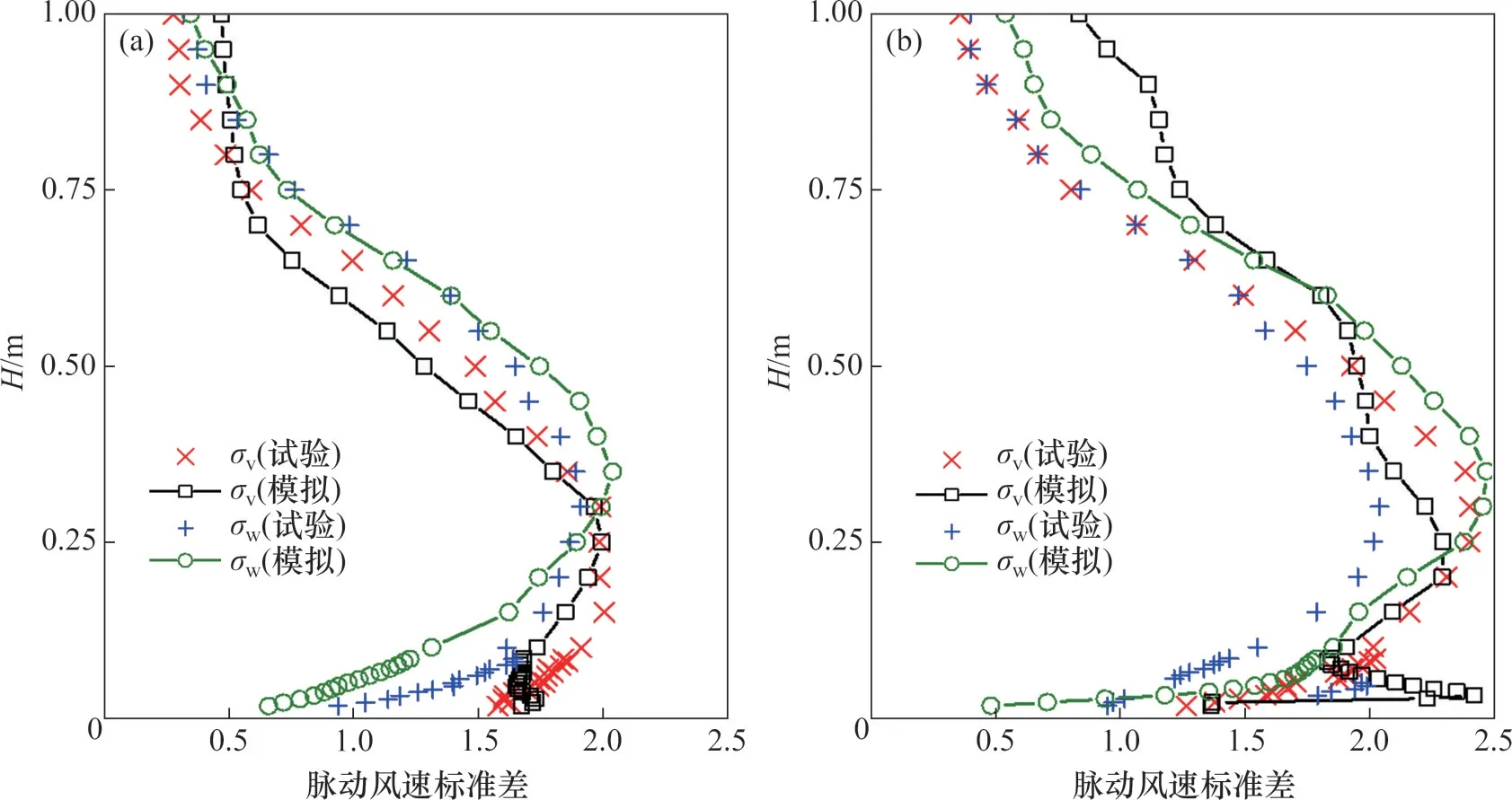
图5 拉萨及成都侧桥塔数值模拟与风洞试验横风向和垂直向脉动风速标准差对比Fig.5 Comparison of σv and σw between numerical simulation and experiment at two bridge towers

从数值上看，大涡模拟获得的脉动风速标准差整体偏大，在本文风向角下，迫龙沟大桥处于前方山体的尾流中，而大涡模拟可能会高估尾流旋涡[19]，从而得到偏大的脉动风速标准差。上流山体距离拉萨侧桥塔更远且山体的海拔较低(如图1(a)所示)，因此，拉萨侧桥塔处大涡模拟结果更加准确。近壁面脉动风速标准差误差较大，误差可能来源有：1)风洞试验中地形模型由泡沫塑料板层叠而成；表面粗糙高度较难估计，故壁面粗糙高度模拟不准确；2)近壁面旋涡结构复杂，数值模拟难度较大。而在高度为0.5 m以上的高空中，大涡模拟准确度较高。

综上所述，大涡模拟与风洞试验的平均风速和脉动风速标准差随高度变化趋势均较吻合，误差在可以接受的范围内，故本文大涡模拟的结果可信、有效。

2.2 入口来流对高山峡谷风场特性的影响

入口来流为均匀来流和边界层来流时，大涡模拟获得的平均风速剖面如图6(方形标志)所示。从图6可见：在2种来流条件下，入口边界的平均风速剖面完全不同(如图3(b)所示)，但桥塔位置的平均风速剖面类似，说明桥塔处风场特性主要受上流地形控制，入口来流类型对其平均风速剖面影响较小；与均匀来流相比，边界层来流工况下的平均风速偏小，两者的相对偏差主要出现在高度为0.25～0.75 m 范围内，近壁面和高空中相对偏差较小，拉萨侧和成都侧桥塔平均风速的最大相对偏差分别为-16.51%和-24.67%。另外，在边界层来流下，拉萨侧和成都侧桥塔的梯度风高度分别为0.9 m和1.0 m，略大于均匀来流工况下的梯度风高度，说明边界层来流下桥址处大气边界层发展更为充分。

入口来流为均匀来流和边界层来流时，大涡模拟获得的顺风向、横风向和垂直向脉动风速标准差剖面如图6(圆形标志)和图7所示。从图6和图7 可见：在这2 种来流条件下，入口边界的脉动风速标准差(均匀来流无脉动风速标准差)剖面不同，但不同高度顺风向、横风向和垂直向脉动风速标准差的变化趋势类似。入口来流类型对拉萨和成都侧桥塔处的脉动风速标准差影响不同，脉动风速标准差有较大差别。在高空中，边界层来流下的脉动风速标准差均比均匀来流下的大，高空中的脉动风速标准差主要来源于入口添加的湍流。边界层来流下拉萨侧桥塔低空中的σu比均匀来流下相应值高4%；边界层来流下在高度为0.1 m 以下的σv明显大于均匀来流下的相应值，相对偏差约为30%。边界层来流下成都侧桥塔低空中的σu较小，与均匀来流下的相应值最大相对偏差达-69.3%。在高度为0.25 m 以下时，两桥塔处的σw受入口来流类型影响均较小，边界层来流和均匀来流下的垂直向脉动风速标准差比较接近。上述对比结果说明入口湍流会增强高空中的脉动风速标准差，而低空中的脉动风特性不仅受入口来流类型的影响，而且与上流地形有较大关系。

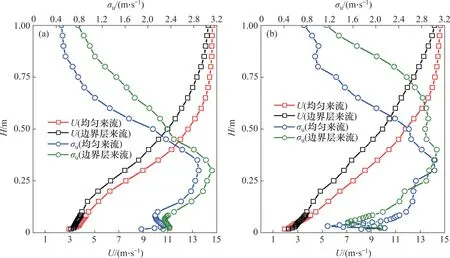
图6 均匀来流及边界层来流时拉萨及成都侧桥塔平均风速和顺风向脉动风速标准差对比Fig.6 Comparison of U and σu between uniform flow and boundary layer flow at two bridge towers

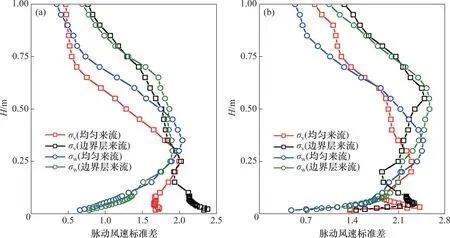
图7 均匀来流及边界层来流时拉萨及成都侧桥塔横风向和垂直向脉动风速标准差对比Fig.7 Comparison of σv and σw between uniform flow and boundary layer flow at two bridge towers

2.3 高山峡谷瞬时风场特性分析

为深入研究入口来流类型对桥塔位置风场特性的影响，绘制桥址中心的速度云图剖面。在均匀来流下，垂直桥轴线方向的速度云图如图8(a)所示。从图8(a)可见：气流通过上流山体时产生气流分离，上流山体脱落的旋涡向下流运动，同时向高空发展，在地形模型下流位置基本耗散。上流山体背风侧产生了多个尾流区，迫龙沟大桥桥址位于尾流范围中，风场特性受地形影响较大。在边界层来流下，垂直桥轴线方向的速度云图如图8(b)所示。从图8(b)可见：上流山体气流分离造成的气流加速现象没有均匀来流下的明显，山体前方气流减速范围更大。与均匀来流工况相比，在边界层来流下上流山体气流分离点远离入口，山体脱落的旋涡可以达到离山体更远的距离；山体后方尾流区没有明显的分区，旋涡连成一片，在桥址上方形成大片尾流区；导致桥址所处位置的旋涡结构更加复杂，尾流区高度更大。综上可知，入口湍流会导致桥址处平均风速降低，而脉动风速标准差增大。

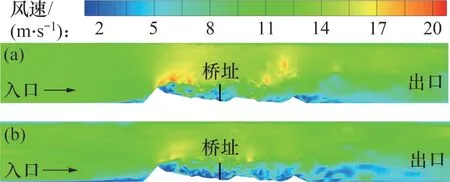
图8 垂直桥轴线方向瞬时速度云图剖面Fig.8 Contour of instantaneous velocity in direction of vertical bridge axis

均匀来流下沿桥轴线方向的速度云图如图9(a)所示。从图9(a)可见：迫龙沟大桥位于“U形”峡谷中，受上流山体尾流的影响，峡谷内没有明显的加速效应。边界层来流下，沿桥轴线方向的速度云图如图9(b)所示。从图9(b)可见：添加平均风速剖面导致高空中风速更大，上流山体产生的旋涡影响区域更大，气流流经峡谷左侧山体时，产生了更加剧烈的加速效应；拉萨侧桥塔靠近峡谷，其风场特性主要受上流地形影响，而成都侧桥塔处于前方山体的尾流中间，风场特性对入口来流类型更加敏感。

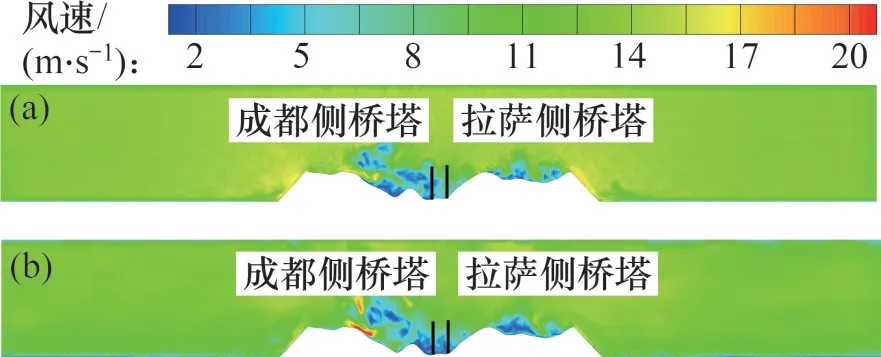
图9 沿桥轴线方向瞬时速度云图剖面Fig.9 Contour of instantaneous velocity along bridge axis

3 结论

1)大涡模拟得到的高山峡谷桥址处平均风速剖面和脉动风速标准差剖面与风洞试验相应结果较吻合，最高相关性系数可达0.99 以上，两者之间的误差较小，可认为大涡模拟的结果是可信的。

2)入口湍流对桥址处平均风速剖面和脉动风速标准差剖面形状影响不大，边界层来流时平均风速较均匀来流时低，高空中的脉动风速标准差较均匀来流时高。低空中脉动风速标准差不仅受入口来流类型影响，而且与上流地形有较大关系。

3)边界层来流下桥址大气边界层发展更充分，高山峡谷梯度风高度大于规范推荐值(300～450 m)，与高山峡谷周围的最大高差相近。

4)边界层来流会使上流山体处的气流分离点后移，同时增大尾流区范围，并使尾流区旋涡结构更加复杂。