高温下射流管伺服阀流量特性分析

訚耀保，郭文康

(同济大学 机械与能源工程学院，上海，201804)

电液伺服阀是电液伺服控制系统的核心部件，可将电信号转换为相应的流量和压力信号，以控制机械执行器的输出位移和力，具有体积小、功率放大率高、线性度好、响应速度快、运动平稳可靠等优点[1-2]。KRIⅤTS[3]研究了气动射流管伺服阀的前置级简化模型和参数，分析了两级伺服阀结构参数与阀静态、动态性能的映射关系。SOMASHEKHAR 等[4]建立了射流管伺服阀的集中参数数学模型，并利用有限元方法研究射流管伺服阀特性，获得了反馈杆的反馈力随射流管偏转位移变化的表达式，提高了仿真精度。力矩马达作为射流管伺服阀的核心驱动装置，其性能直接影响伺服阀的整体性能。众多学者从磁路漏磁、加工装配误差等多个方面对力矩马达及射流管伺服阀的静动态特性进行了研究[5-11]。随着高性能材料的发现，逐渐出现了智能材料驱动的射流管伺服阀，该类射流管伺服阀具有更高的响应速度和更大的带宽[12]。GARCIA 等[13]研究了离心力对电液伺服阀零偏的影响，建立了地震实验台数学模型。訚耀保等[14]建立了三维离心环境下射流管伺服阀零偏特性的数学模型，提出了抑制三维离心环境下射流管伺服阀零偏值的措施。学者们也对偏转板式射流伺服阀进行了研究。李双路等[15]建立了考虑射流盘尺寸和形位误差时的流场仿真模型，通过分析射流盘的形状因素与压力特性之间的关系，实现了借助神经网络算法对不同形位误差组合下的射流盘两腔恢复压力的预测。延皓等[16]推导了偏转板式射流伺服阀前置级液动力的简化计算公式，并将其与Fluent液动力压力差计算法和实验测量法进行比较，验证了所提公式的可行性。在伺服阀的温度特性研究[17-18]中，多借助数值模拟软件来模拟热平衡过程以及分析热-流-固耦合问题，较少涉及伺服阀的前置级流动过程研究。

射流管伺服阀前置级流体的射流流动过程复杂，在目前分析中通常对其进行较大程度的简化，且高温下流体流动状态的变化机理尚不明确。为了揭示射流管伺服阀前置级流体流动过程中的能量传递机制，本文建立射流管伺服阀前置级数学模型，分析高温下射流管伺服阀的流量特性，探究前置级结构参数与射流管伺服阀流量特性之间的映射关系。

1 射流管伺服阀工作原理

图1所示为射流管伺服阀示意图，射流管伺服阀主要由力矩马达、射流管前置放大级和滑阀功率放大级构成。射流管由衔铁枢轴支撑，可绕枢轴摆动。导油管与射流管相连接，油液从射流管射出后，部分油液进入到接收器的2 个接收孔内，两接收孔分别与滑阀的两腔相连接。油液通过射流喷嘴将压力能转化为动能，被接收孔接收后，又将动能转化为压力能。当力矩马达无电流输入时，射流管伺服阀处于零位，喷嘴相对于2个接收孔处于几何中立位置即对称位置。喷嘴喷出的流体均等地进入2个接收孔，流体动能在接收孔内转化为压力能，滑阀两端的压力相等，滑阀处于中位，射流管伺服阀无流量输出。当有电流输入时，力矩马达产生使射流管偏转的扭矩，射流管组件绕着转轴旋转，喷嘴偏离中立位置，使其中一个接收孔接收的流体多于另一个接收孔接收的流体，在滑阀两端的容腔内形成压差，推动滑阀阀芯产生位移，输出流量；同时，在衔铁组件偏转和滑阀阀芯移动过程中，反馈杆组件产生对射流管的反馈力矩和对滑阀阀芯的反馈力，当射流管受到的反馈力矩与力矩马达产生的偏转扭矩相平衡时，衔铁组件处于稳定位置；同时，当滑阀阀芯两端的压力差与滑阀的液动力和反馈力之和相平衡时，阀芯停止运动。阀芯位移与输入的控制电流呈比例关系，当负载压差一定时，阀的输出流量与控制电流成正比。

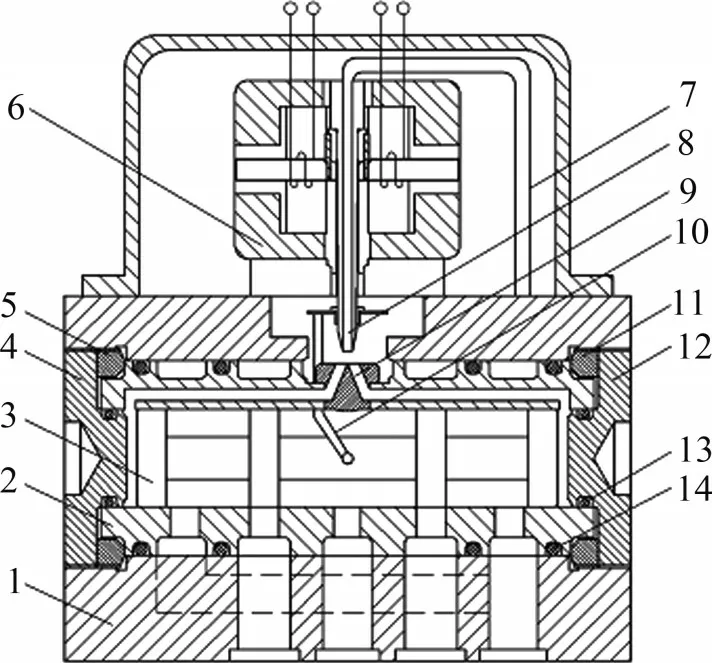
图1 射流管伺服阀示意图Fig.1 Schematic of jet-pipe servo valve

2 数学模型

射流放大器结构如图2所示，射流管伺服阀前置级主要由射流喷嘴与接收器组成，喷嘴后端与导油管连接。图2 中，ps为供油压力；pb为截面B上的油液压力，可近似等于系统的回油压力pe；v0为流过截面B流体的平均速度；ds为导油管直径；d1为射流喷嘴直径；d2为接收孔直径；θ为喷嘴收缩角；l2为喷嘴的自由射流距离；接收器中两接收孔对称分布，与竖直方向呈夹角α；Δ为分流劈厚度。射流放大器的工作过程可大致分为3 个阶段：1)第1 阶段，油液从导油管入口处(截面A)流入，经导油管和射流喷嘴流出，该阶段内，高压油液的压力能转化为动能；2)第2阶段，油液从射流喷嘴中高速流出，射入同种介质中，形成淹没射流，之后到达接收器上表面(截面C)；3)第3 阶段，高速流出的油液进入接收器的2个接收孔中，左右对称分布的接收孔分别与主阀芯左右端面处的封闭容腔相连，待油液充满封闭容腔并达到稳定状态后，阀芯左右两端即形成恢复压力pL和pR，此时在接收孔内，油液的动能重新转化为压力能。

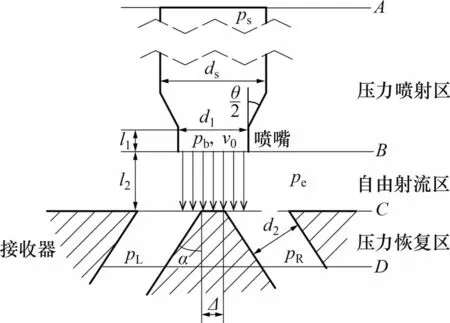
图2 射流放大器结构示意图Fig.2 Schematic diagram of jet amplifier structure

2.1 压力喷射区

在第1阶段中，油液的能量形式由压力能转化为动能，考虑流动过程中的沿程损失和局部损失，并忽略重力势能，则有：

式中：ρ为油液密度；g为重力加速度；ξ1为第1阶段的能量损失系数；l1为射流喷嘴内部圆柱段长度；ξ1a为锥形渐缩流道的局部损失系数，常温下ξ1a可取为0.12；γ为喷嘴出口圆柱段的沿程损失系数；Re为雷诺数；μ为油液动力黏度。

2.2 自由射流区

在射流放大器工作过程的第2阶段中，高速流体从喷嘴喷出，如图3所示，主射流与周围静止流体发生掺杂，掺杂区域随着流体流向下游而逐渐地扩展，形成2 个不同区域，即初始段和主体段。根据文献[19]，圆形自由射流的初始段长度x0为

图3 圆形自由射流流动特征示意图Fig.3 Schematic diagram of free circular jet flow

对于射流管伺服阀中的射流放大器，喷嘴到接收器的距离l2小于初始段长度x0，即流体从截面B到截面C的过程均处于自由射流的初始段。初始段中，距喷嘴出口x处截面上的速度v为

式中：r为流场中的点到射流中心线的距离；re(x)为等速核心区半径；be(x)为射流特征厚度；c为特征厚度系数，根据文献[20]的试验结果，本文取c=0.21。

图4所示为C截面上接收孔的射流接收面积示意图，其中等速核心区半径为R1，剪切层外边界半径为R2，图4 中，R1=re(l2)，R2=re(l2)+be(l2)。在接收断面中，当射流管伺服阀处于零位时，射流束轴线的冲击点为C1，分流劈左、右半侧的厚度分别为Δ1和Δ2。接收孔在接收面上的投影为椭圆，其中a1为短轴，b1为长轴，根据图2所示几何关系可知，a1=d2/2，b1=d2/(2cosα)。由于射流喷嘴与接收器之间的距离l2非常小，故射流束移动的距离即可视为射流喷嘴的偏移距离xn。

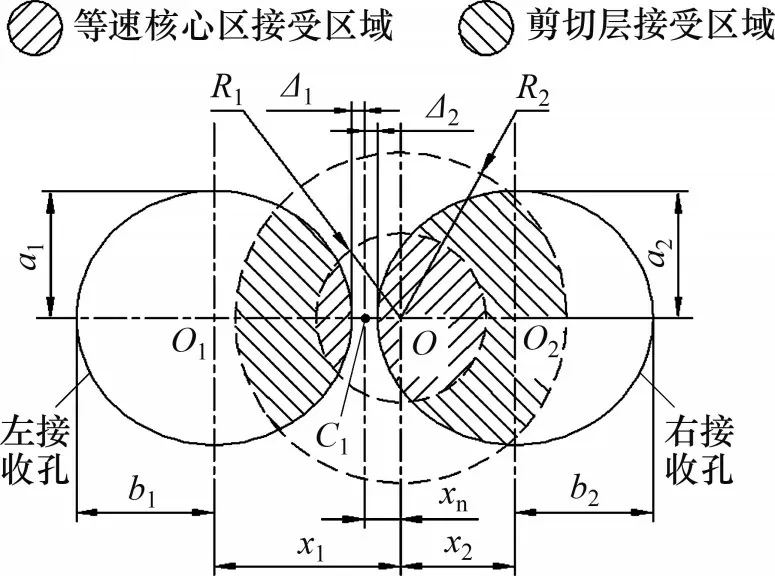
图4 射流放大器接收孔的射流接收面积示意图Fig.4 Schematic diagram of receiving area of jet amplifier receiver hole

在额定电流驱动下，射流管伺服阀的射流喷嘴偏移量为数十微米，远小于射流发展到C截面时的等速核心区半径；在射流管伺服阀的工作过程中，接收孔内接收到的动量根据速度分布的不同可分为等速核心区和剪切层接收区两部分。其中，等速核心区形状为橄榄形，剪切层接收区为弧形。

橄榄形等速核心区流量接收示意图如图5所示，橄榄形等速核心区域的面积Apo为接收面上接收孔和射流中等速核心区重叠区域的面积。图5中，Rr为接收孔半径，Rr=d2/2。由于接收孔在接收面的投影为椭圆形，定义K=1/cosα，则橄榄形等速核心区的实际面积A′po与Apo的关系为

由图5 中的几何关系可知，橄榄形区域面积Apo等于扇形MOrN与扇形MON面积之和减去四边形MOrNO的面积。橄榄形等速核心区域的面积Apo[21]为

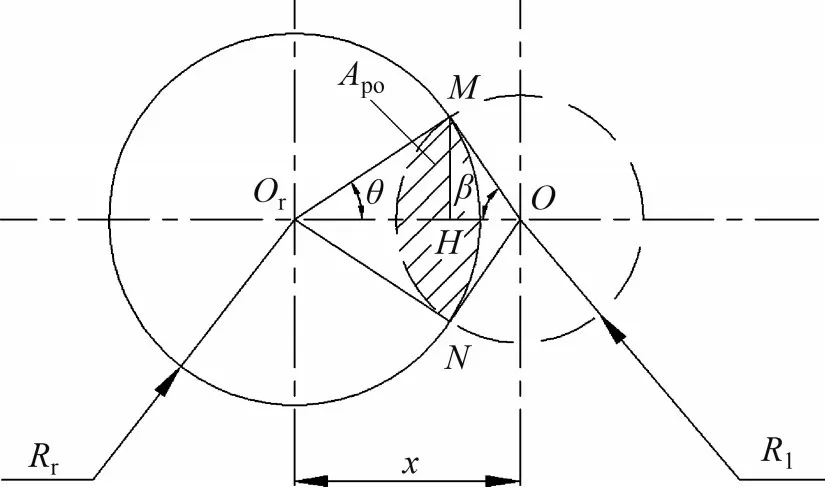
图5 橄榄形等速核心区流量接收示意图Fig.5 Schematic diagram of flow receiving of olivary potential core zone

橄榄形等速核心区的接收动量Jpo为

式中：lOrH为线段OrH的长度；lOrM为线段OrM的长度；lOH为线段OH的长度；lOM为线段OM的长度；Rrk为某一侧接收孔的半径，xk为某一接收孔中心与射流中心之间的距离，k=1，2；Jpo为橄榄形等速核心区的接收动量。

弧形剪切层示意图如图6所示。弧形剪切层接收面积可由大橄榄形面积和小橄榄形面积相减得到，同理可推导得到弧形剪切层接收区域动量Jma为

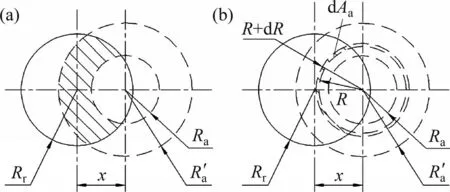
图6 弧形剪切层示意图Fig.6 Schematic diagram of curved shear layer

式中：Ra为弧形剪切层内边界的半径；R′a为弧形剪切层外边界的半径；dAa为环状微元面积。

考虑到左、右接收孔轴线与接收器界面中垂线呈夹角α，则接收孔在接收界面内呈椭圆形，故单侧接收孔接收到的总动量Jr可表示为

单侧接收孔的总接收面积Ain为

2.3 压力恢复区

在射流放大器工作过程的第3阶段中，油液的能量形式由动能重新转化为压力能。图7所示为右侧接收孔处的三维流场示意图。选定图7中截面C与截面D之间区域为控制体(高度为h)，在控制体内，动量守恒。图8所示为射流与接收面在截面C上的投影，结合图7和图8可知，进入到接收孔内的动量中一部分因与劈尖碰撞而损失，损失的竖直方向上的动量Jr0为

图7 接收孔处三维流场示意图Fig.7 Diagram of the three-dimensional flow field at the receiving hole

式中：Ah为碰撞壁面的投影面积。

由图8可见：碰撞壁面的投影面积为弧形，可通过大橄榄形区域的面积减去小橄榄型区域的面积得到Ah：

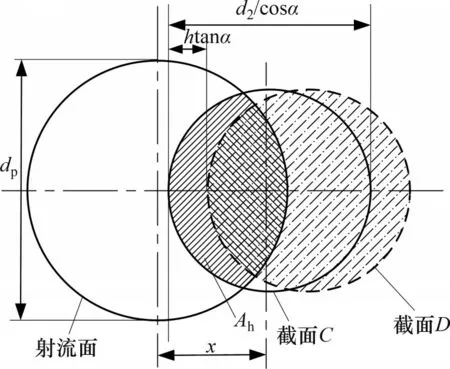
图8 射流与接收面在截面C处的投影Fig.8 Projection of jet and receiving surface at section C

根据流量守恒公式可知，流量连续性方程为

由式(18)可推导得到出流流量的动量J4：

在控制体内，根据动量守恒定理，有

式中：J4为出流动量；Jr为流入动量；Jr0为射流过程中因碰撞损失的动量；J3为恢复界面上的力。

通过动量定理可求得右侧接收孔内的恢复压力pR为

式中：Sr为接收孔在截面D处的横截面积；pR为截面D处的恢复压力。

从能量角度对第3阶段进行分析，接收孔内油液流动示意图如图9所示，高速流体以平均速度vin从面积为Ain的孔射入，油液在由截面C运动到截面D的过程中，动能转化为压力能，则有

式中：ξR2为第3阶段中右接收孔的能量损失系数，其代表接收孔内流入和流出的两股油液之间相互卷吸造成的能量损失。

根据图9及流量连续性方程可知，油液从流入接收孔到流出接收孔，总的能量损失ΔER可表示为

图9 接收孔油液流动示意图Fig.9 Schematic diagram of oil flow in receiving hole

式中：ξR为流体从流入接收孔到流出接收孔过程的总能量损失系数，可以看出其仅与结构参数有关。

总能量损失包括与壁面作用的沿程损失ΔER1、两股流体相互作用的能量损失ΔER2以及流体从接收孔流出时的局部能量损失ΔER3。

根据边界层理论[22]，流体与壁面作用的沿程损失ΔER1可表示为

式中：lin和lout分别为流体流入和流出接收孔的边界层长度。流体从接收孔流出的能量损失ΔER3为

式中：ξR3为接收孔出流的能量损失系数；Cd3为流体从接收孔流出的流量系数，在阀口流动的雷诺数Re较高时，近似为定值，取Cd3=0.61。

由于接收器内流体的速度较大且边界层长度较短，ΔER1≪ΔER3，在后续的计算中，可忽略流体与壁面作用的沿程能量损失。此外，两股流体间的相互作用力对流入和流出流体造成的能量损失相同，有

根据式(18)和式(23)～(28)可求得第3 阶段右接收孔的能量损失系数ξR2：

当温度变化时，能量损失发生变化，但仍遵循式(24)。其中，ΔER2和ΔER3对应的能量损失系数ξR2和ξR3仅与流道的结构参数有关，且总能量损失系数ξR为定值，故ΔER1对应的能量损失系数应保持不变。射流管电液伺服阀的工作介质为航空10 号液压油，当温度升高时，黏度会产生较大幅度下降，根据式(25)，流体流入和流出接收孔的边界层长度lin和lout会相应增加，即图7中的h相应增加，进而导致接收孔内的恢复压力发生变化。

2.4 主阀芯运动方程

主阀芯在其两端压差作用下移动，其运动方程为

式中：Ft为主阀芯的驱动力；mv为阀芯与阀腔油液的综合质量；Bv为阀芯与阀套间的黏性阻尼系数；Bf0为阀芯瞬态液动力产生的阻尼系数；kf0为阀芯稳态液动力的弹性系数；Fi为负载力；xv为主阀芯开口量。

主阀芯的驱动力Ft为

式中：Av为主阀芯阀肩横截面面积；pc为主阀芯左、右两端恢复压力的差值，pc=pL-pR。

稳态流量特性是伺服阀的静态特性，电液伺服阀滑阀一般为负开口四通滑阀，故其空载输出流量Qc为

式中：Cd为阀口节流系数；w为滑阀节流口面积梯度；U为滑阀副的正遮盖量。

3 理论结果及试验验证

3.1 射流管伺服阀空载流量变化幅度的理论计算结果

当供油压力一定时，伺服阀的流量与滑阀的开口量xv有关，而滑阀的开口量与主阀芯两端的恢复压力差值成正比。当伺服阀工作温度变化时，油液的黏度发生变化，主阀芯两端的恢复压力差pc随之改变，导致伺服阀的额定流量发生相应变化。伺服阀在小信号电流控制时具有优良的线性度，故在分析中可近似认为恢复压力差pc的变化幅度等于伺服阀空载流量Qc的变化幅度。定义某一温度T附近的空载流量变化倍率λ为

式中：pLT0和pRT0分别为油温为30 ℃时左、右接收孔内的恢复压力；QcT0为油温为30 ℃时伺服阀的空载流量；pLT和pRT分别为油温为T时左、右接收孔内的恢复压力；QcT为油温为T时伺服阀的空载流量。

根据式(1)～(32)，可对不同接收孔直径下的恢复压力和空载流量特性进行分析。为便于试验对比，分析时取输入电流为额定电流的10%即在射流喷嘴存在极小偏移时进行理论计算。计算时，取射流孔直径d1为定值，接收孔直径d2为变量。为研究高温下伺服阀空载流量随温度的变化情况，首先根据前置级数学模型计算得到30 ℃下的接收孔内控制体的高度h以及左右接收孔内的恢复压力pLT0和pRT0，然后，基于图10 中油液黏度随温度的变化情况，根据式(25)计算温度变化后流体流入和流出接收孔的边界层长度lin和lout，并通过图7所示几何关系得到变化后的控制体高度h，随后计算得到温度升高后的恢复压力pRT和pLT，最后根据式(33)得到空载流量的变化倍率λ。当温度变化ΔT=120 ℃(从30 ℃增至150 ℃)时，计算得到射流孔与接收孔直径比对空载流量的影响，如图11所示(图11 中，l2为射流管伺服阀自由射流距离)。由图11可以看出：伺服阀的空载流量变大，且射流孔与接收孔的直径比会影响空载流量的变化倍率；伺服阀空载流量的变化幅度存在极小值，此时，因油液黏度的下降导致射流碰撞面积Ah的变化幅度最大，碰撞损失的动量Jr0增加，并部分抵消了图7中控制体内Jr和J4因射流速度变化而增加的动量，故此时空载流量的整体变化倍率最小，射流孔直径与接收孔直径比值约为0.69。当接收孔直径减小时，常温下的射流碰撞壁面长度h逐渐增加，最终达到最大值，即射流碰撞面积Ah达到最大值，此后，伺服阀空载流量的变化与射流碰撞面积Ah无关，仅受射流速度的影响；当接收孔直径增加时，常温下射流碰撞壁面长度h逐渐减小，直至壁面处由碰撞损失的动量Jr0可忽略不计，此后空载流量的变化同样仅受射流速度的影响。本文选取Ⅰ型和Ⅱ型2种射流管伺服阀，其中Ⅰ型伺服阀中射流孔直径与接收孔直径比值约为0.686，Ⅱ型伺服阀中射流孔直径与接收孔直径比值约为0.900，分别对应于图11中A1和B1点。

图10 10号航空液压油的运动黏度-温度特性曲线Fig.10 Kinematic viscosity and temperature characteristic curve of No.10 aviation hydraulic oil

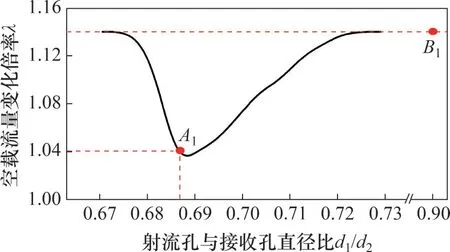
图11 射流孔与接收孔直径比对空载流量的影响Fig.11 Influence of the diameter ratio of jet hole and receiving hole on no-load flow

改变射流管伺服阀中的自由射流距离l2，根据式(6)和(7)得到此时接收截面处的速度分布和面积分布，并根据上述计算方法得到射流孔与接收孔直径均不变时，空载流量受温升的影响情况。图12所示为温度变化ΔT=120 ℃(从30 ℃增至150 ℃)时，射流管伺服阀中自由射流距离对空载流量的影响。当空载流量变化幅度未饱和时，射流管伺服阀的自由射流距离会影响射流碰撞面积Ah的变化幅度，进而影响空载流量的变化幅度。由图12(a)可知，在Ⅰ型射流管伺服阀中，当1.7＜l2/d1＜2.5时，空载流量受温升影响较小。由图12(b)可以看出：在Ⅱ型伺服阀中，在不改变Ⅱ型射流管伺服阀中射流孔和接收孔直径的前提下，改变自由射流距离l2不会改变空载流量受温度的影响情况，且在ΔT=120 ℃时，空载流量变化倍率始终为1.14。

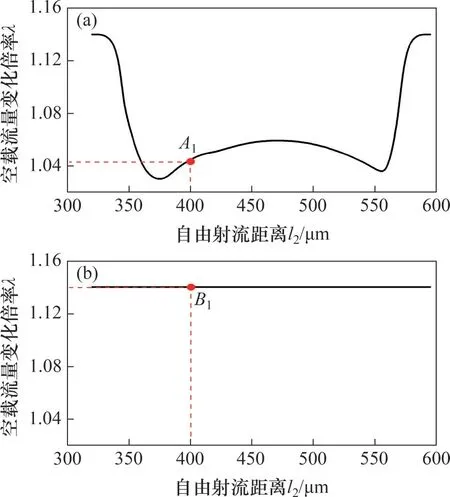
图12 高温下射流管伺服阀自由射流距离对空载流量的影响Fig.12 Influence of the free jet distance of jet pipe servovalve on the no-load flow at high temperature

3.2 射流管伺服阀恢复压力特性试验结果分析

射流管伺服阀恢复压力特性测试装置如图13所示。试验过程中保持阀芯与反馈杆始终分离，保证恢复压力对喷嘴位移无反馈，可以在开环条件下直接得到控制电流i与恢复压力pc的映射关系。此外，在主阀芯左右端盖之中分别接装压力计，测量阀芯两端控制腔内的恢复压力，液压万用表型号为WEBTEC。试验流体介质为10 号航空液压油，试验时油液温度保持在25～30 ℃，供油压力为8 MPa，回油背压0.6 MPa。使用伺服放大器提供伺服阀的控制电流，力矩马达两线圈为并联连接。试验中，控制电流从-20 mA 开始，间隔2 mA，增加至20 mA，之后仍间隔2 mA，再将控制电流逐渐降至-20 mA；分别记录各电流对应的左右接收孔恢复压力pL和pR，并计算得到阀芯两端的恢复压力差pc。试验对象为Ⅱ型射流管伺服阀，其前置级主要结构参数如表1所示。

图13 射流放大器恢复压力测试装置Fig.13 Test apparatus of recovery pressure for jet amplifier

表1 Ⅱ型射流管伺服阀主要参数Table 1 Main parameters of type Ⅱ JPSⅤ

以控制电流i为横坐标，将试验得到的恢复压力差pc绘制在二维直角坐标系中；并通过理论计算得到控制电流i对应的射流喷嘴移动距离xjn。

式中：h1为衔铁组件旋转中心与喷嘴末端距离；kt为电流力矩系数；km为磁弹簧刚度；ka为弹簧管刚度；i0为零偏电流；本文试验中h1=9.45 mm，kt=4.3(N·m)/A，km=4.4(N·m)/rad，ka=21.1(N·m)/rad，i0=-11.54 mA。

在同一坐标系中，增加控制电流i对应的xjn刻度，并将xjn作为自变量，根据射流管伺服阀前置级数学模型，计算得到相应的恢复压力差pc。射流放大器恢复压力特性试验与理论结果对比如图14所示。由图14 可以看出：射流前置级恢复压力差的理论计算值与试验值基本一致，验证了前置级数学模型的正确性。

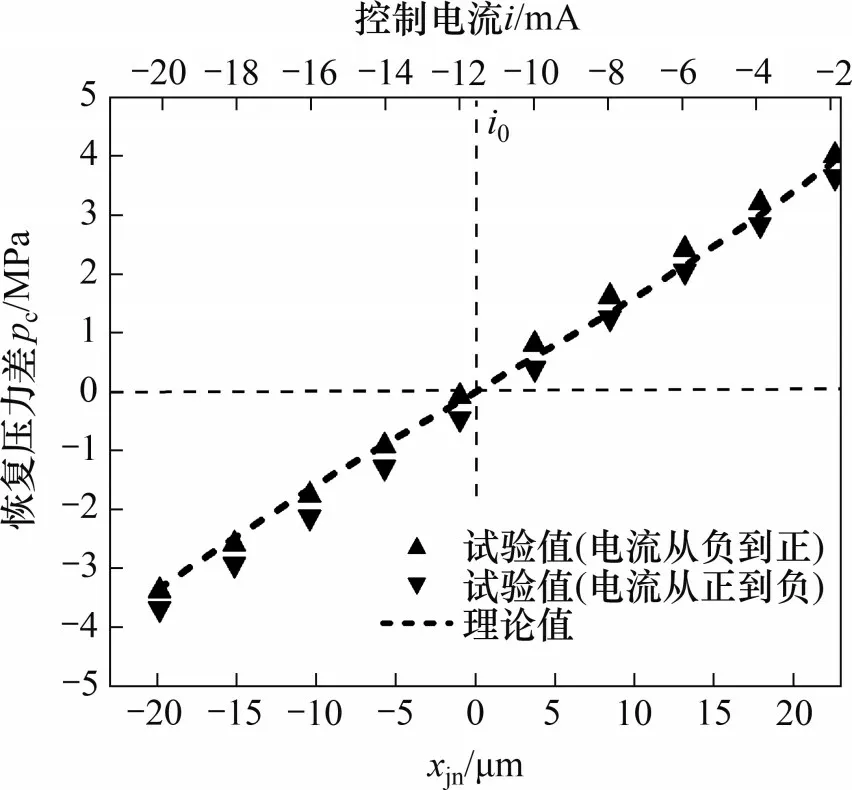
图14 射流放大器恢复压力特性试验与理论结果对比Fig.14 Comparison of the experimental and theoretical results of the recovery pressure characteristics of jet amplifier

3.3 射流管伺服阀小信号空载流量试验结果分析

在高温液压试验台上进行射流管伺服阀的流量特性试验，试验介质为10 号航空液压油，液压试验台最大供油压力为35 MPa，最大输出流量为250 L/min，最高油液温度可达160 ℃，温度控制精度为±2 ℃。空载流量特性是电液伺服阀静态特性的一种，它可以表征电液伺服阀的多项静态特性指标，在电液伺服阀的性能判定中起重要作用。小信号空载流量特性曲线是指输入电流幅值为10%额定电流时对应的伺服阀空载流量曲线。根据试验曲线，可计算得到不同温度下空载流量、流量增益、死区等伺服阀零区特性指标。

图15所示为Ⅰ型射流管伺服阀在工作温度分别为30 ℃和150 ℃时的小信号空载流量特性曲线，该型伺服阀的主要结构参数如表2所示，空载流量试验结果和理论计算结果的对比如表3所示。由图15、表2和表3可以看出：高温下Ⅰ型射流管伺服阀的空载流量、零位流量增益以及死区基本不变，理论结果与试验结果较为吻合。

表2 Ⅰ型射流管伺服阀主要参数Table 2 Main parameters of type Ⅰ JPSⅤ

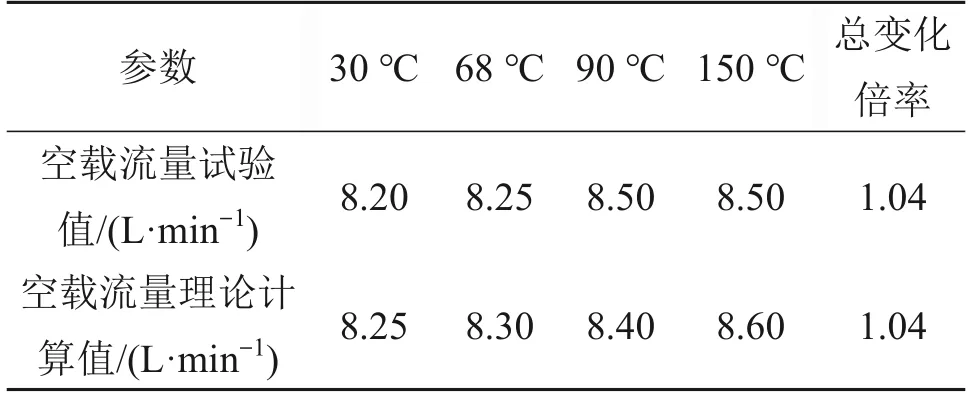
表3 Ⅰ型伺服阀小信号空载流量理论及试验结果Table 3 Theoretical and experimental results of small signal no-load flow of type Ⅰ JPSⅤ

图15 Ⅰ型伺服阀小信号空载流量特性曲线Fig.15 Small signal no-load flow curve of type Ⅰ JPSⅤ

图16所示为Ⅱ型射流管伺服阀在工作温度分别为30 ℃和150 ℃时的小信号空载流量特性曲线。空载流量试验结果和理论计算结果的对比如表4所示。由图16和表4可以看出：高温下，Ⅱ型射流管伺服阀的空载流量、零位流量增益均小幅度上升；当温度由30 ℃增至150 ℃时，试验得到的空载流量变化幅度为16%，理论计算得到的空载流量变化幅度为14%，理论与试验结果变化趋势一致，且总变化幅度较为吻合。

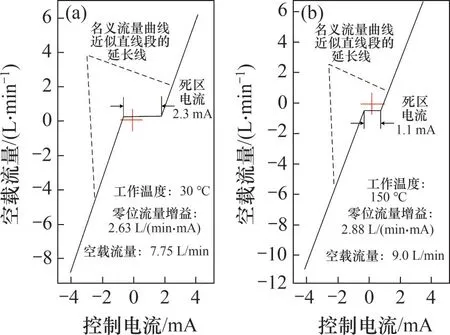
图16 Ⅱ型伺服阀小信号空载流量特性曲线Fig.16 Small signal no-load flow curve of type Ⅱ JPSⅤ

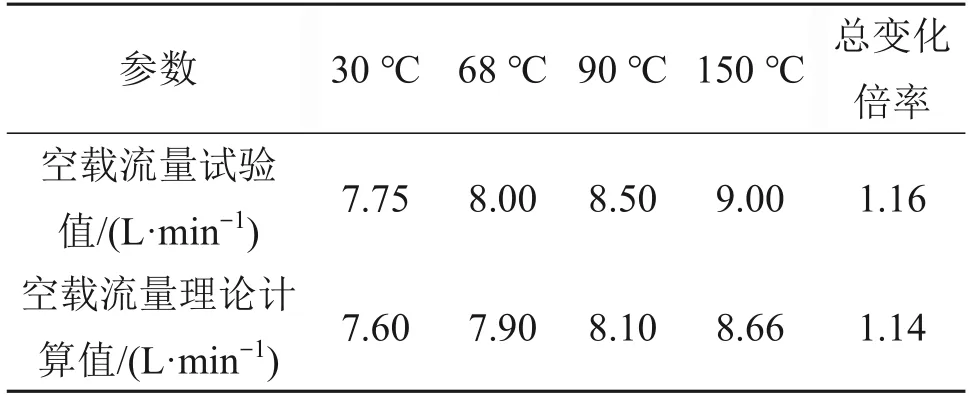
表4 Ⅱ型伺服阀小信号空载流量理论及试验结果Table 4 Theoretical and experimental results of small signal no-load flow of type Ⅱ JPSⅤ

4 结论

1)将射流管伺服阀前置级分成压力喷射区、自由射流区和压力恢复区，基于动量守恒和能量守恒定理，建立了射流管伺服阀的前置级数学模型，并通过恢复压力特性试验进行了验证。

2)高温下油液黏度的降低导致射流管伺服阀的射流速度增大，恢复压力增加，空载流量变大。在120 ℃温差下(由30 ℃增至150 ℃)，当射流孔与接收孔直径的比值为0.69 时，射流碰撞面积的变化最大，射流过程中因碰撞损失的动量增加，一部分因射流速度变化而增加的动量被抵消，此时，伺服阀恢复压力和空载流量的变化最小；当空载流量变化幅度未达最大值时，射流管伺服阀的自由射流距离会影响射流碰撞面积的变化，进而影响空载流量的变化幅度。