四级固体运载火箭弹道设计及运载能力分析
何 磊,张 雯,董晓彬
(北京宇航系统工程研究所,北京 100076)
0 引言
随着卫星互联网及各类遥感卫星星座的推出,未来中低轨卫星市场体量巨大,正在建立新的社会经济形态[1]。全固体运载火箭具有发射设备简单、操作简便、发射保障要求低、发射准备周期短、能全天候发射等优势,具备海陆通用、快速响应的特点,可为中/小型卫星提供更为灵活和经济的发射方式,也可满足快速响应发射和星座灵活补网需求,日渐受到军民商发射领域的广泛青睐[2-3]。
固体运载火箭是航天运输系统的重要组成部分,美、俄、欧盟、日本等航天强国和组织在发展液体运载火箭的同时均发展了固体运载火箭,形成了完善的航天运输体系。我国在固体运载火箭领域通过预研牵引,支持了固体运载火箭120/200 t大推力固体发动机前期研究和关键技术演示验证工作,当前已形成长征十一号、捷龙系列、力箭一号等全固体运载火箭低、中运载能力覆盖的搭配布局。
然而,通过分析我国固体火箭的运载能力可以发现,在2~3 t(500 km太阳同步轨道)运载能力区间的固体火箭存在“缺位”。因此,本文基于已成功试车的最大推力500 t、直径3.5 m整体式大型固体发动机[4],通过已有固体动力模块化组合或者级间优化配置,形成一款运载能力3 t左右的四级全固体运载火箭,以有效填补我国固体火箭运载能力空档。
火箭总体设计的主要目的之一就是满足运载能力要求,因而运载能力分析是运载火箭总体方案论证和初步设计阶段的重要研究内容。运载能力分析的主要内容是弹道分析,主要有积分法和估算法两大类[5]。积分法即仿真分析法,是用比较精确的数学模型,通过计算机进行大量的计算,求解出火箭的最大运载能力。综上分析,本文首先给出了新型四级全固体运载火箭构型;然后通过建立三自由度弹道计算仿真模型,明确弹道设计/优化变量和指标,构建了弹道优化模型;在此基础上采用仿真分析法对火箭从发射至入轨全过程进行仿真,并分析了该火箭构型典型弹道曲线特点,以及各级结构质量、推重比和末级装药量对运载能力的影响规律,为未来固体火箭的总体方案论证提供依据。
1火箭构型及弹道方案概述
1.1 火箭构型
本文论证的固体运载火箭采用四级固体串联构型,箭体最大直径3.5 m,总长约39 m,起飞质量约260 t,适配Φ3.35 m和Φ4.2 m两种整流罩,可实现海陆通用发射。该火箭构型外形简单,火箭长细比(11.14)合理,满足设计要求。运载火箭固体发动机性能参数见表1,后文将围绕该火箭构型及表1所列发动机开展仿真研究。
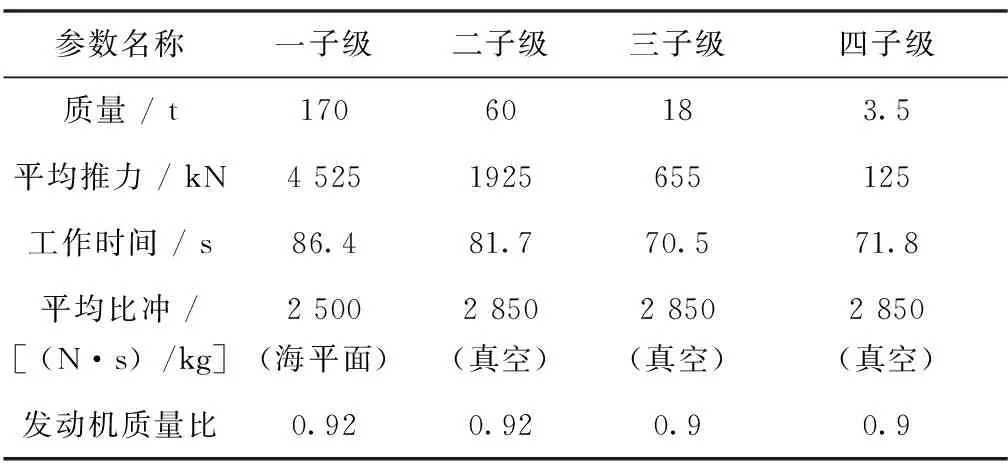
表1 发动机性能参数
1.2 弹道方案
对于四级固体运载火箭,发射轨道高度为2 000 km 以下的卫星,发射段弹道多采用助推+滑行[6]形式:一级起飞后采用攻角转弯的方式,一级后段及二级前段采用重力转弯的方式;二级飞出稠密大气层后,程序角按照一定速率下压;二三级分离后,火箭开始滑行,滑行结束后三级发动机点火;三级动力飞行前段程序角按常值变化率下压/上抬,之后定轴飞行直至三级飞行结束;三四级分离后,四级沿转移轨道滑行到合适的高度后四级发动机点火,直至发动机耗尽点卫星入轨。俯仰程序角曲线[7-8]如图1所示。
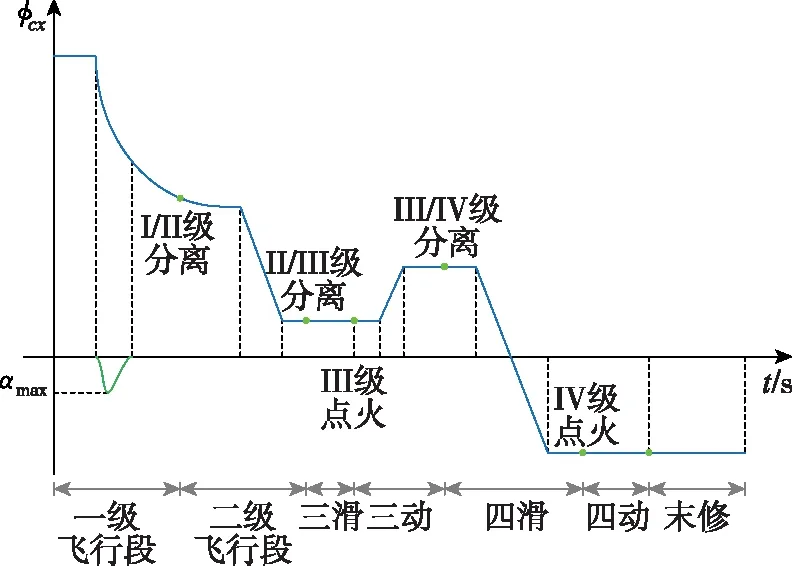
图1 俯仰程序角曲线示意图Fig.1 Schematic diagram of pitch program angle
攻角转弯段攻角变化规律如下
(1)
式中
αm为攻角转弯段攻角极值(绝对值),tm为攻角达到极值时的时间。
2 弹道计算及优化模型
2.1 弹道计算模型
2.1.1 动力学模型
对固体火箭的运载能力进行分析时,采用瞬时平衡假设,认为火箭无惯性地转动且控制系统理想,此时只考虑火箭的质心动力学方程,而不考虑火箭的绕质心转动动力学方程。任一变质量质点在惯性坐标系中的质心动力学矢量方程为[9]
(2)
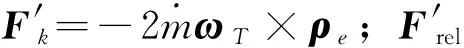
2.1.2 质量模型
给出假设条件如下:固体运载火箭在装药量变化时各级直径不变;在推力一定的情况下,装药量变化时各级级间段、前封头、后封头、喷管质量不变,只有发动机柱状段因装药量变化引起的加长或缩短的质量变化;固体推进剂装药选择圆孔装药类型,di和Di分别为第i级装药的初始内孔直径和外圆直径;hi为第i级发动机柱状段壁厚;ρti为第i级燃料密度;ρi为第i级发动机壳体密度。
固体运载火箭总起飞质量可表示为[10]
(3)
(4)
式中,m0为运载火箭起飞质量,mdy为有效载荷质量,mtz为整流罩质量,mti为第i级原始燃料质量,mfji为第i级固体火箭发动机结构质量,mgi为第i级级间段质量,Δmfji为发动机柱状段结构质量变化量,Δmti为第i级燃料变化量。
2.1.3 气动力模型
采用标准大气模型(GB1920-80),气动力可在速度系内分解为阻力X、升力Y和侧力Z,按式(5)计算。
(5)
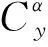
2.1.4 引力模型
采用地球椭球模型,考虑J2项对引力影响,主要参数采用1975年第十六届国际大地测量协会的推荐值(IAG-75),引力在地球矢径与地球旋转方向的投影为
(6)
式中,J=3J2/2,μ为地球引力系数,Re为地球赤道半径,φ为地心纬度,r为地心矢径。
2.1.5 推力模型
推力矢量P=[P0 0]T中的推力大小按式(7)计算
(7)
式中,Psl为一级发动机海平面推力,Se为发动机喷口面——Pvac为二、三、四级发动机的真空推力,p0和p分别对应海平面和当前飞行高度的大气压强。
2.2 弹道优化模型
2.2.1 优化问题描述
(1)性能指标
固体运载火箭主动段弹道优化的目的是提高运载能力,即在总体参数保持不变的前提下,对主动段进行能量管理及弹道优化设计以使有效载荷质量最大,因此,目标函数选择为
minJ(u)=-mpayload
(8)
式中,mpayload为有效载荷的质量,u为优化控制变量。
(2)优化控制变量
选取图1中的变量和射击方位角A0作为待优化参数,因此,控制变量为
u=[αm,k3,t4h,φcx4,A0]T
(9)
2.2.2 约束条件
考虑工程可实现性,控制变量应满足一定的约束条件,例如:αm是控制运载火箭初期攻角转弯的关键参数,若αm较大,则转弯幅度大,终端高度小,终端速度大;若αm较小,则转弯幅度小,终端高度大,终端速度小;k3是控制俯仰程序角下压的参数,基于控制系统的要求,一般不超过10(°)/s。此外,还需满足如下终端约束和过程约束:
(1)控制变量约束
umin≤u≤umax
(10)
(2)入轨条件约束
(11)
(3)最大动压、抛整流罩热流与最大飞行过载约束
q≤qmax,W≤Wmax,ny≤ny,max
(12)
2.2.3 主动段弹道优化模型
固体运载火箭主动段轨迹优化设计是一类终端时刻自由、终端状态固定且带有路径约束的多阶段、非线性最优控制问题。
minJ(u)=-mpayload
subj.toEqs.(2),(10-12)
(13)
3 仿真计算结果
基于第1章给定的火箭构型和弹道方案,以有效载荷质量最大为目标,目标轨道选择700 km的太阳同步轨道,对应的入轨点速度、轨道倾角、当地弹道倾角和轨道偏心率分别为7 054.286 m/s、98.187 6°、0°和0。飞行过程中允许的最大动压、抛整流罩热流和最大飞行过载分别为60 kPa、300 W/m2和7g。
3.1 典型弹道曲线特点
依据第1,2章固体运载火箭构型和建立的弹道计算及优化模型,优化结果如表2和图2~4所示。飞行过程中的最大动压出现在一级飞行段,最大动压值为58.12 kPa;抛整流罩时的热流为300.0 W/m2;最大(轴向)过载在三级动力飞行段,最大过载值为6.51g,满足飞行过程约束。

表2 优化设计结果

图2 俯仰程序角随时间的变化曲线Fig.2 Pitch program angle history
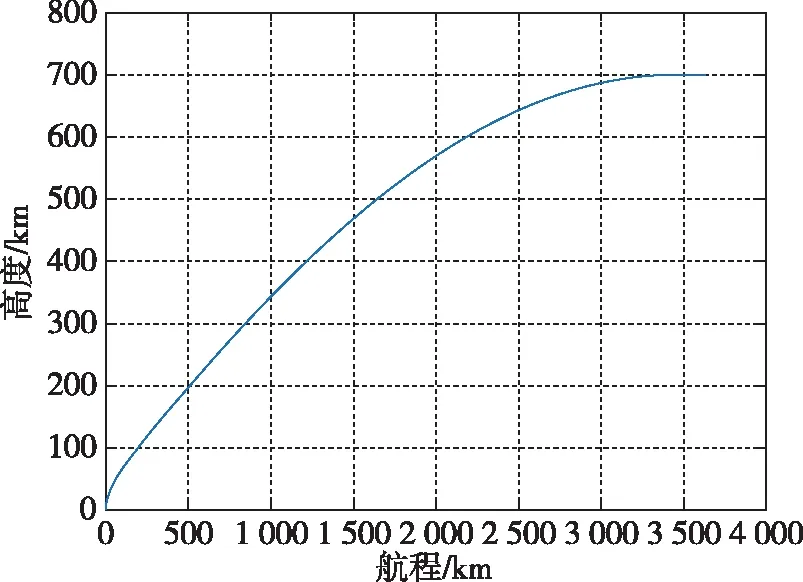
图3 火箭纵向剖面内的飞行轨迹Fig.3 Longitudinal trajectory of rocket
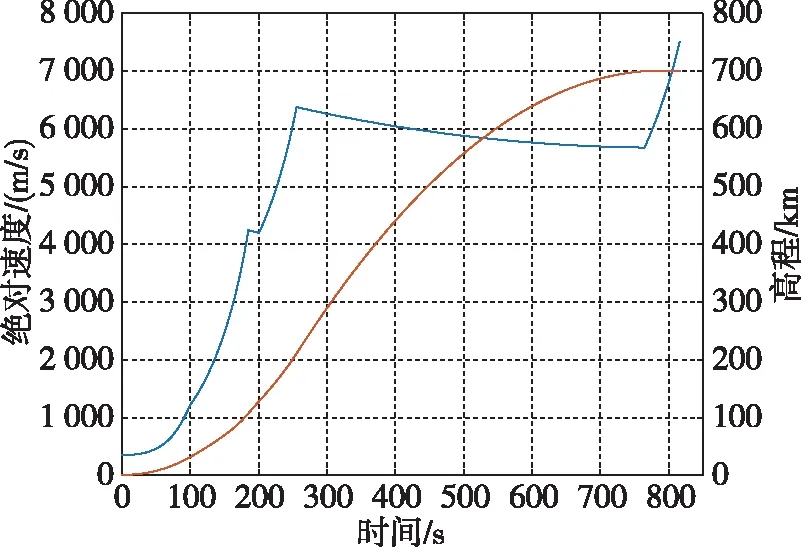
图4 绝对速度、高度随时间的变化曲线Fig.4 Absolute velocity and altitude history
图2为最优弹道对应的俯仰程序角,可以看出,火箭起飞后各阶段对应的程序角变化特点有很大不同,第一、二级飞行段基本位于大气层内,在动压、热流和过载约束的情况下,应尽可能减少速度的损失,因此在经过垂直上升段和攻角转弯段后,这一阶段的大部分时间均处于零攻角飞行状态。如图3所示,火箭在这一飞行阶段依靠重力缓慢地转弯,有利于尽快飞出稠密大气层,减少气动阻力带来的速度损失。
当火箭进入真空环境后,飞行过程约束逐渐消失,这一阶段的程序角要满足入轨的高度和速度约束。绝对速度和高度随时间的变化曲线如图4所示,在三级动力飞行段和四级滑行段,最显著的一个特征是飞行高度的急剧增加,速度的变化相对比较缓慢,而在四级动力飞行段的变化趋势则正好相反,飞行高度基本不变,绝对速度急剧增加至入轨所需速度。从上述结果可知,由于固体火箭发动机只能耗尽关机,且具有工作时间短、推力大等特点,火箭在真空飞行中采用“助推--滑行--助推”的飞行模式有利于最大限度地将尽可能多的有效载荷送入轨道。
3.2 弹道计算与优化模型的应用与分析
本节依据第1,2章给定的固体运载火箭构型和建立的弹道计算及优化模型,分析研究了各级结构质量、推重比和末级装药量对极限运载能力的影响。
固定各级发动机装药量,各级结构质量对运载能力的偏导数如表3所示。从表中可见,三、四级结构质量对运载能力的偏导数分别是-0.473 6和-1.0,即三、四级结构质量每减小10 kg对应增加的运载能力为4.736,10.0 kg,明显大于一、二级结构质量对运载能力的影响。
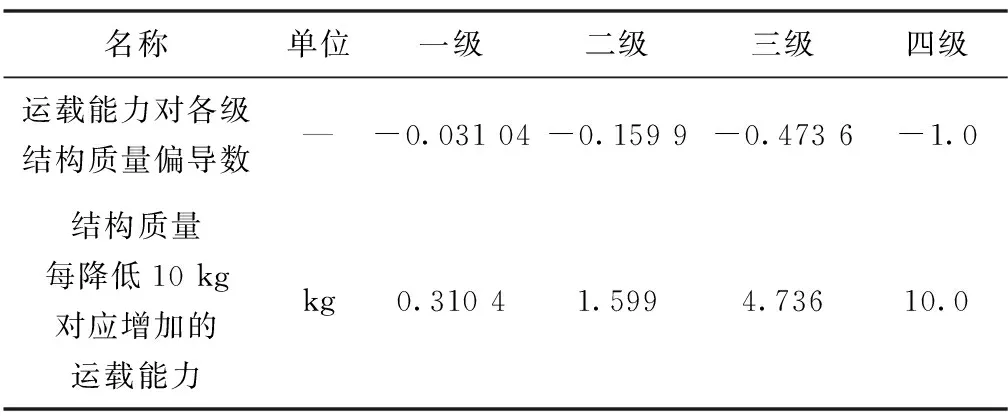
表3 各级结构质量对运载能力的偏导数
假定一级发动机的总能量(或总冲)不变,则发动机推力F1与工作时间Δt1之间的关系为:Δt1=Δm1Isp1/F1(Δm1和Isp1分别为一级发动机的装药量和比冲)。
从图5和图6中可知,只改变一级发动机推力,火箭推重比与对应的极限运载能力和飞行过程中的最大动压均呈正相关关系。推重比在1.2~2.0区间时,对极限运载能力的影响较大(推重比由1.2提升到2.0时的运载能力提升约21%),推重比超过2.0时,增大推重比对运载能力的影响有限(推重比由2.0提升到2.6时的运载能力提升约2.2%)。推重比越大,飞行过程中的最大动压也就越大(两者之间为近似的线性关系),引起的载荷、热等相关飞行环境越恶劣,火箭总体设计时需要综合考虑。
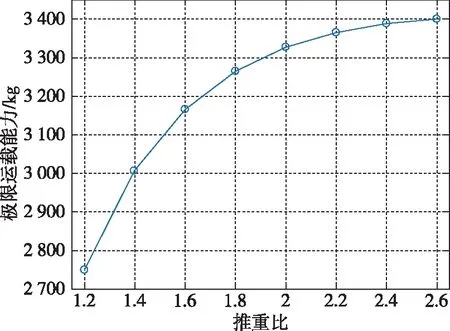
图5 推重比与极限运载能力之间的关系Fig.5 Relationship between the thrust-weight ratio and ultimate capacity

图6 推重比与最大动压之间的关系Fig.6 Relationship between the thrust-weight ratio and maximum dynamic pressure
根据第3.1节的分析结论可知:四级构型固体运载火箭的末级动力飞行段主要是给运载火箭提供速度增量。当末级发动机的装药量增加时,可提供的末级速度增加,记为ΔV1,但末级发动机装药量增加同时也使得前三级发动机工作时的消极质量增加,进而带来末级发动机点火时刻初始速度减小,记为ΔV2。当ΔV1>ΔV2时,运载能力呈增加趋势,反之则呈减少趋势;当ΔV1=ΔV2时末级发动机装药量达到理论上的最优值。以上描述趋势与图7中运载能力仿真结果的变化趋势吻合。从图7中可知,只改变四级发动机装药量,火箭的极限运载能力随装药量呈先增大后减小的趋势,末级发动机装药量约为4 500 kg时对应的运载能力达到最大。

图7 末级装药量与极限运载能力的关系Fig.7 Relationship between the charge mass of upper stage and maximum lift capacity
4 结论
本文针对我国固体运载火箭运载能力在2~3 t(500 km太阳同步轨道)区间上存在“缺位”的现实,首先给出了一款运载能力3 t左右的四级全固体运载火箭构型。然后建立了固体运载火箭三自由度弹道计算和优化模型,通过仿真手段分析了典型弹道曲线的特征,得出在大气层内飞行时,弹道设计应尽可能降低速度损失,而当火箭进入真空环境后,采用“助推--滑行--助推”的飞行模式有利于最大限度地将尽可能多的有效载荷送入轨道。此外,还进一步分析了各级结构质量、推重比和末级装药量对运载能力的影响规律。其中,三、四级结构质量每减小10 kg对应增加的运载能力为4.736,10.0 kg,明显大于一、二级结构质量对运载能力的影响;推重比由1.2提升到2.0时的运载能力提升约21%,同时飞行过程中最大动压也会显著增大;火箭的极限运载能力随末级装药量呈先增大后减小的趋势,四级发动机装药量为4 500 kg 时对应的运载能力达到最大。上述分析结论为未来固体火箭总体方案论证提供依据。

