深度学习理念下的小学数学教学策略研究

程华

摘要：深度学习是一种课堂变革的理念和课堂教学的设计思路。深度学习指的是促进学生在课堂教学中全身心积极参与、体验成功、获得发展的有意义的学习过程。小学数学深度学习的发生以理解数学学科本质为基础，通过教师引导，培养学生的数学思维能力和问题解决能力。教学中，教师要引领学生深度参与和体验，通过体验式学习，激发学生的情感投入；通过结构式学习，增强学生的数学整体意识；通过反思式学习，提升学生的理性思维。

关键词：数学深度学习；情感投入；整体意识；理性思维

深度学习是一种课堂变革的理念和课堂教学的设计思路。所谓深度学习，指的是在教师的引领下，学生围绕着具有挑战性的学习主题，全身心积极参与、体验成功、获得发展的有意义的学习过程。在这个过程中，学生掌握学科的核心知识，理解学习的过程，把握学科的本质及思想，形成积极的内在学习动机、高级的社会性情感、积极的态度、正确的价值观，成为既具有独立性、批判性、创造性，又有合作精神、基础扎实的优秀学习者。

深度学习理念下的数学学习，需要在学习新知的时候，教师能在学生原有认知的基础上，找到学生的“最近发展区”，让学生在不知不觉中感受到：这些数学知识的产生和发展不是人为编造，强加于他们的，而是在他们“灵魂”深处本来就有的。教师要准确把握学科及学科教育的本质设计教学，以唤醒学生“灵魂”深处已有的东西——知识、方法、经验，引导学生自主构建新的认知体系，逐渐形成探索、发现、研究特质。这些也正是深度学习教学的核心目标——更好地关注学生的学。

一、 借助体验式学习，激发学生的数学情感投入

小学数学深度学习强调引导学生主动参与数学学习活动，在参与学习活动过程中形成数学基本经验。体验式学习需要引导学生积极探索、发现、经历数学知识的形成过程，以数学知识体验为前提、以数学能力提升为中心建立学生与数学内容之间的紧密联系，进而精确地把握数学学科本质，提升数学核心素养。在小学数学教学中，教师要聚焦数学知识与现实生活之间的联系，基于学生已有生活经验设置问题情境，这样更有利于学生参与教学活动。下面以“厘米的认识”与“1千克有多重”为例进行说明。

【示例1】“厘米的认识”

本节课，教师可给学生创设一个生活化的情境：让学生用牙签、火柴、硬纸条等量一量数学书的同一条边。经过实践操作，在测量数学书同一条边长时，有的学生量出的是6根火柴的长度，有的学生量出的是3根牙签的长度，有的学生量出的是2个硬纸板的长度。“为什么同样数学书的同一条边，量出的数值却有所不同呢？”学生根据测量的经验与观察发现：原来测量所用的工具是不一样的。以数学书边长为情境引入，给学生不同物体作为参照物进行比大小，发生认知冲突，明确需要统一测量的标准，引出1 cm的概念。

接着，教师引导学生层次化体验1 cm的长度：

（1）把学具1 cm的小棒放在手掌中感受长短；

（2）把1 cm的小棒放在两个指尖中感受1 cm有多长；

（3）找一找生活中的1 cm。

通过建立与日常生活之间的联系，在数学知识构建上强调其现实背景与实际意义，可促使深度学习真正发生。这样的教学符合教育教学规律与学生数学学习心理，因此学生可以通过有意义的学习获得成功的数学体验，强化在数学学习过程中的情感投入。

【示例2】“1千克有多重”

物体有轻有重，多重是1千克？学生在一开始学习时是很难清晰感知到的。教师应以生活化的实物为载体，让学生层次化体验1千克的重量，促进深度探究：

（1）出示体积反差比较大1千克棉花糖和1千克盐，让学生先用眼睛觀察大小，再称一称，学生发现都是1千克，形成认知冲突；

（2）掂一掂1千克的物体，感受1千克；

（3）通过掂一掂，对1千克有体验后，寻找生活中质量接近1千克的物体，通过抓豆子比赛，进一步巩固1千克质量的体验。

这样生活化的情境和层次化的体验活动，丰富了学生的体验，使学生经历了从对1千克的质量很不准，到比较准，再到非常准的修正过程，使1千克质量标准在学生体验中由模糊到清晰。

引导学生进行体验式学习是把数学生活化，课堂体验化，体验层次化，以学生的课堂参与体验为主，感官参与越多，学生的记忆就越深刻。这样，学生在不断参与和深度体验中进行了深度学习。体验式学习能够引导学生从被动接受到主动参与，自觉地想一些问题。有了自主意识，深度学习就能真正发生。

二、借助结构式学习，增强学生的数学整体意识

深度学习强调内部整合，将点状的、零散的、碎片化的数学知识整合成整体化、系统化、逻辑化的数学知识结构；根据核心知识共同拥有的本质属性和相同的逻辑关系确定好学习主题，找准关键问题的发力点；整体探析与理解数学学科本质，凝练数学教学目标与主题，围绕教学主题展开教学的整体设计，了解学生探究这一数学主题时存在的概念与方法方面的困惑。

教师要通过整合与之相关领域的数学核心内容，促进学生对数学知识结构的深度理解，引导学生进行结构式学习。结构式学习的关键在于对知识进行深度加工，把知识从碎片化走向结构化，让知识有机地联系在一起，帮助学生形成数学整体意识，从而切实从表层学习引向深度学习。下面以“三角形的分类”与“生活中的负数”为例进行说明。

【示例1】“三角形的分类”

在学习三角形分类前，学生先认识三角形、点、角、线等表层符号知识，教师再引导他们建构三角形各元素之间的深层联系。

教师基于学生的认知经验设计结构式的问题：三角形有几个顶点，几条边，几个角？

学生对线段的认识有：边是线段，线段有长短。学生可根据经验对三角形进行分类：一般三角形、等腰三角形和等边三角形，其中等边三角形是特殊的等腰三角形。

学生对角的认识有：角有大小，根据角的大小分类，三角形可以分为钝角三角形、直角三角形、锐角三角形（如下页图1）。

这样设计，综合考虑了数学学科各知识之间的相互联结，实现了将碎片化的知识有机地结合在一起，通过构建知识结构体系，帮助学生获得数学知识的“生命力”。学生一旦具备数学整体意识，就可以在原有认知结构中不断同化与之相关或相近的数学知识，从而形成数学知识群，这与深度学习的结果是一致的。

【示例2】“生活中的负数”

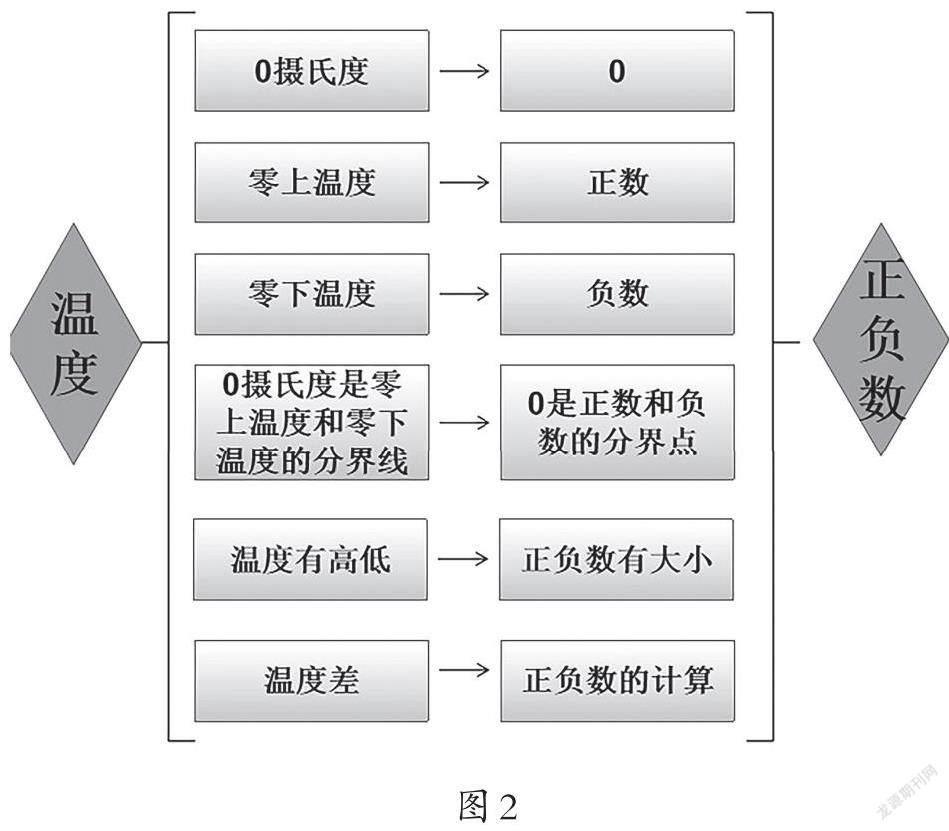
例如，北师大版数学教材四年级上册 “温度”一课，是“生活中的负数”单元主题下的一节先导课。温度是学生现实生活的一部分，温度中有0摄氏度，零上温度，零下温度，0摄氏度是零上温度和零下温度的分界线，温度有高低，有温度差。温度的产生和发展与正负数的产生与发展在原理上是一样的（如图2、图3）。

教师要通过温度的学习实现单元整体教学，把单元知识结构化，打通温度与正负数之间的关系。而温度计是数轴的现实模型，这样就完成了学习正负数时从形象思维到抽象思维的转化。

教师引导学生进行结构式学习，能够把碎片化的知识结构化，帮助学生建构知识结构以及认知结构，在整体上对数学知识和方法进行把握，有利于单元整体教学。改变碎片化处理数学知识和方法的现象，还能增强学生学习数学的整体意识，促进深度学习。

三、借助反思式学习，提升学生的数学理性思维

深度学习是引发学生持之以恒地追问和不断深入思考的学习过程。在教学中，教师应鼓励学生不断发现和提出问题，并能积极地分析和解决问题，在问题链中产生深刻思考。在学习新知时，认知冲突对学生而言具有重大的价值，深度学习的课堂教学中要引发学生的认知冲突，使学生从认知冲突中进行反思，再去发现不足。教师不但需要纠正学生的错误，更需要让学生尝试，并引导学生在不断尝试过程中实现知识迁移。学生在反思过程中，能够更好地从数学视角或跨学科视角发现问题、提出问题、分析问题、解决问题，通过对问题解决方案构建与运用，持续培养数学理性思维。下面以“笔算除法”为例进行阐明。

【示例1】“笔算除法”

笔算除法12÷3时，教师可引导学生思考：除法竖式应该怎样写？

在掌握了加减法和乘法的竖式计算基础上，有的学生会认为：

从学生的认知来看，该方法源于对加、减、乘竖式格式的知识迁移，而有的学生源于课前的自学，会这样写： [4] [3][12][12][0]

教师提出问题：两种竖式形式哪种更合理呢？（引发认知冲突）

然后，教师引导学生重温除法意义——平均分。

师：那12÷3表示什么意义呢？表示把12平均分成3份，每份是几个？

师（实物演示）：老师拿来12个苹果，平均分到3个盘子里，每个盘子分到4个，老师手中一个也没有了。老师手中的12是1个12，而盘子里的12是3个4，这两个12有区别吗？

在演示分物的过程中，教师不能用原有竖式形式，需要改变为新的竖式形式，因为这样能更好地记录平均分的过程。

【示例2】乘法分配律：（a+b）×c=a×c+b×c或（a-b）×c=a×c-b×c

认识了乘法分配律后，学生在知识迁移过程中也会思考：为什么没有除法分配律呢？

例如，在计算（42+14）÷7时学生发现，（42+14）÷7=42÷7+14÷7=6+2=8。因此，在计算48÷（4+8）时，有的学生也这样算48÷（4+8）=48÷4+48÷8=12+6=18。这就引发了学生的认知冲突，使他们比较48÷（4+8）=48÷12=4和48÷（4+8）=48÷4+48÷8=12+6=18这两种算法，确定哪一种是正确的。显然第一种方法是正确的，第二种方法是错误的。

教师引导学生进行反思：你有什么疑问吗？

生：（42+14）÷7=42÷7+14÷7=6+2=8，这样做对不对？

生：为什么（42+14）÷7=42÷7+14÷7=6+2=8可以像乘法分配律那样做，而48÷（4+8）=48÷12=4这个就不行呢？

生：有没有除法分配律呢？

教师利用“问题链”进行教学设计，以问题解决来推动教学活动的开展，并将学习内容纳入学生原有认知结构，实现已有数学知识在新的问题情境中的合理迁移和“生长发育”，帮助学生体会数学本质。经过比较、分析与讨论，学生明白了乘法分配律不适用于除法。（42+14）÷7可以等于42÷7+14÷7在本质上是平均分，把两个数的和平均分成7份，可以把两个数分别平均分成7份，再把分得的数合起来。而48÷（4+8）不等于48÷4+48÷8，是因为两次平均分的标准发生了改变。

引导学生进行反思式学习，需要激发学生的认知冲突，教师要鼓励学生大胆质疑，使学生不断进行反思，有利于批判质疑与创新思维的发展，有助于学生像数学家那样对问题进行深入地思考，提升反思能力与质疑精神，实现深度学习。

深度学习下的课堂教学中，教师应为学生提供多元的、综合的学习素材，帮助学生刻画出单元主题内容清晰且连续的学习轨迹，以学定教，顺学而导，在课堂中引领学生深度思考，深度体验，打通知识到核心素养的通道。

参考文献：

［1］王燕.静悄悄，让学习有深度——例析小学数学深度学习策略［J］.数学教学通讯，2022（7）.

［2］李晓梅，张秋，张丽欣.基于深度学习的“种子课”教学设计案例探析——以北师大版小学数学教材五年级上册“平行四边形的面积”为例［J］.辽宁教育，2020（23）.

（責任编辑：杨强）