“双减”政策下初中数学作业设计的“五优”策略

徐静

摘 要：落实“双减”政策，优化数学作业.本文从优化数学作业增强作业的趣味性、加强数学作业的阅读性、设计数学作业的层次性、落实数学作业的合作性、拓宽数学作业的开放性五个方面浅谈作业设计优化的有效策略.

关键词：双减；数学作业；优化；策略

在“双减”政策之下，国家强调减轻学生的作业负担，全面落实素质教育，提高学生的综合素养，这就要求数学老师在教学过程中落实作业布置的问题，不能再呈现给学生的是那些知识定位差、内容完全统一、形式非常单一、问题过程过于封闭甚至是机械抄写的作业，需要的是让学生跳出题海，在作业设计理念和模式上有新的改变，考查学生的问题也不仅仅是掌握知识，更重要的是体现数学核心素养和知识内涵的延伸.这就要求我们数学教师在作业设计上要注意科学化、合理化、综合化^［1］.那么如何对数学作业进行优化设计呢？本文针对初中数学作业的设计简单地提出几种策略并进行分析.

1 优化数学作业，增强数学作业的趣味性

兴趣能使得人在认识过程中整个心理活动变得积极化，能使得观察更加敏锐，记忆力得到加强，想象力会变得更加丰富，由此克服困难的能力也会得到加强，智力发展也会大大提高.因此在数学作业设计上，如果增强作业的趣味性，会更好地激发学生的学习兴趣，作业质量也会得到很大的提高.

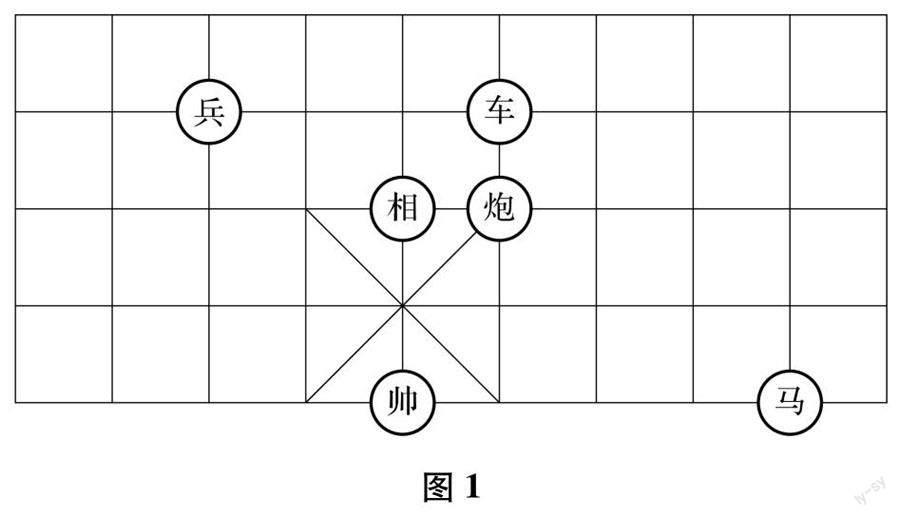
例如在教学“平面直角坐标系”相关内容时，渗透加入中国象棋的一些益智游戏来引导学生确定点的位置.图1是一局象棋残局，若“帅”位于点（-1，-2），“马”位于（3，-2），试判断原点的位置.

在学习“勾股定理”“对称图形”等相关知识过程中，将“七巧板”的一些问题融入其中，这样不但激发了学生学习的兴趣，更引导学生从课内到课外的延伸学习.

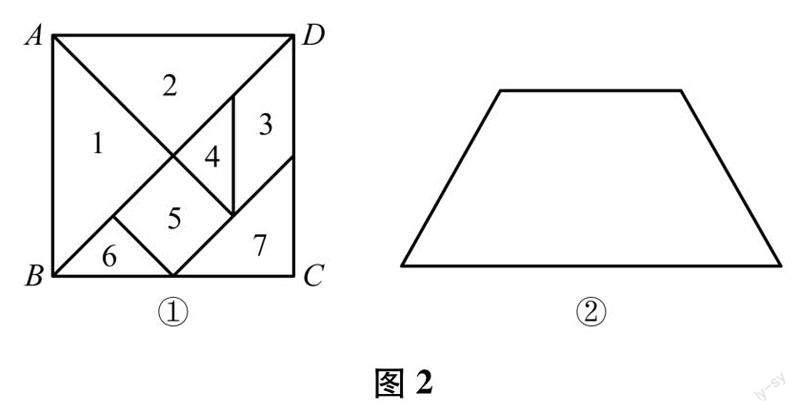
比如设计如下问题，七巧板是由正方形ABCD分割成7小块组成的（其中标号为1、2、4、6、7的是等腰直角三角形，标号为5的是正方形，标号为3的是平行四边形），如图2-①所示，图2-②中的等腰梯形是由七巧板怎样拼得的？画出你的拼法.

此类游戏问题的设计，不但激发了学生的观察能力，还增强了学生动手操作、问题判断能力，既增强了符号感，又加强了几何直观能力及其应用意识.

2 优化数学作业，加强数学作业的阅读性

加强数学作业的阅读性，不但让学生感受数学语言的符号化，更多的是培养学生阅读思考的能力.只有不断思考才能不断理解内化数学语言的特殊性，才能感知材料中所体现的相关数学术语和符号，只有这样才能在感知的过程中体会到数学原理之间的逻辑关系，达到真正认知材料的内涵体现^［2］.同时，阅读的体现，也让部分偏文的学生激发了学习兴趣，突破感知困难，自觉进行逻辑推理思维训练.

例如我们在学习了“一元二次方程”相关内容后制定如下作业问题：

请阅读下面相关的材料，并按照解决相关的学习任务：人类从古至今对一元二次方程的研究经历了漫长的岁月，一元二次方程及其解法最早出现在公元前两千年左右的古巴比伦人的《泥板文书》中.到了中世纪，阿拉伯著名的数学家花拉子米在他的代表作《代数学》中给出了关于“一元二次方程”的一般解法，并结合几何法图示给予相关的证明.我国古代三国时期的数学家赵爽也给出了类似的几何解法.

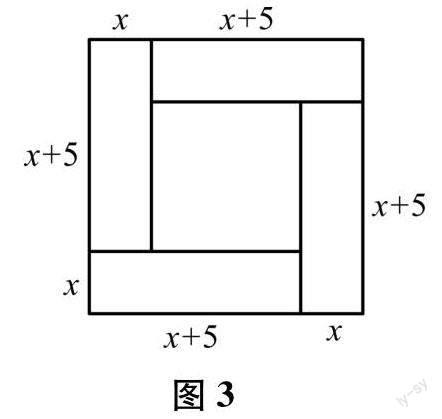
赵爽在其所著的《勾股圆方图注》中记载了解方程x²+5x-14＝0，即x（x+5）＝14的方法.首先构造了如图3所示的图形，图中的大正方形面积是（x+x+5）²，其中四个全等的小矩形面积分别为x（x+5）＝14，中间的小正方形面积为5²，所以大正方形的面积又可表示为4×14+5²=81，据此易得x＝2.

学习任务：

（1） 请你参照上述所展示的图解一元二次方程的操作，在图4的三个构图中选择能够说明方程x²-4x-12＝0的正确构图是                  （从序号①②③中选择）.

（2） 请你认真阅读上述材料，根据其方法特点，在图5的网格图中设计一个正确的构图，利用相关的几何法求解方程x²+2x-15＝0（写出必要的思考過程）.

通过阅读，引导学生感知一元二次方程与几何图解方法之间的联系，并借助相关问题的提出，激发学生对题目中所给知识的正确理解，不但考查了阅读所给材料的理解和运用的能力，还从多个方面体现解题方法，起到对学生综合素养的考查的作用.

3 优化数学作业，设计数学作业的层次性

数学作业对于学生来说较为困难，因此部分学生很容易就放弃对问题的研究.如果我们在设计过程中多多考虑学生的个体差异，尽可能多地关注到每一位学生的能力水平，体现问题的层次性，让学生真正在解答过程中跳跳够得着，努把力能过关，加把油就能完成任务，也许会大大提升作业的效果，使学生真正做到“减负”.

例如在学习了“平面图形的认识”的相关内容后，设计如下问题：

一天张老师看到两个小围棋爱好者在下棋之余摆出来棋子形状，他们在一张白纸上画出如图6所示的图案并摆上棋子，第一幅图上摆有4颗棋子，第二幅图上摆有9颗棋子，第三幅图上摆有16颗棋子，…，依次按此规律排列下去.

针对上述的情景描述，可以分别设计成如下层次性作业，引导学生逐步解答.

（1） 第5个图案中有                     个棋子，第6个图案中有                     个棋子.

（2） 根据上述规律，求出第n个图案中棋子的个数（用含n的代数式表示）.

（3） 是否存在恰好由2022个棋子排列出的具有上述规律的图案？若存在，说明它是第几个图案？若不存在，请说明理由.

通过这一系列的问题研究，學生在起初把握图形特点的基础上能进一步灵活运用，并慢慢地尝试着用已经学会的知识来化解有难度的问题，再通过逐渐深入的问题探究，不仅拓宽了知识面，还加强了对知识点的拓展延伸，激发训练了学生的数学思维.

4 优化数学作业，落实数学作业的合作性

长期以来，作业都是老师布置学生训练，老师和学生都是唱着“独角戏”，作业阅读越枯燥，慢慢地变为“应付”.改变方式方法，势在必行.将“独角戏”变为“对台戏”，变为“大合唱”，角色转换或者合为一体，既体现教师的“师”之导，又能体现“生”之练，效果非常佳.

例如在教学“测量”和“解直角三角形”等相关内容时，根据情况多方面设计学生团队合作方面的问题.

要求班级一个数学兴趣小组测量旗杆的高度，同学们发现系在旗杆顶端的绳子垂到地面并多出一段（如图7-①），聪明的小迪发现：先测出绳子多出的部分长度为m米，再将绳子拉直（如图7-②），测出绳子末端C到旗杆底部B的距离为n米，利用所学知识就能求出旗杆的长，若m＝6，n＝12，可否测量得到旗杆AB的长？若小迪在C处，用手拉住绳子的末端，伸直手臂（拉绳处E与脚底F的连线与地面垂直），后退至将绳子刚好拉直为止（如图7-③），测得小迪手臂伸直后的高度EF为2米，小迪需要后退几米？

整个问题在室外操作计算完成，单独一人是不能完成的，提高了合作性，既增添学生学习的兴趣，又调动了积极性.

5 优化数学作业，拓宽数学作业的开放性

随着新课程标准的实施，对学生的最终要求目标已经不是简单的掌握知识技能，更多的是培养全面发展的具有良好思维品质的研究性、创新性人才，这就需要我们数学教师在作业设计上多给学生以开放性的空间，积极引导学生发散思维、创造性思维，才能满足相关要求，落实到核心素养的培养上来^［3］.开放性的问题设计恰恰体现了这些要求.这类作业的设计往往体现在结论或者条件的不确定性、结论的不固定性或者思路的创新性等，在引导学生解决此类问题的过程中，往往更多的是探求过程的思路开发，思维变化的创造性.

当然，布置作业不是学生的负担，而是对学生学习质量的一种检测.在“双减”背景下，主要目标是减轻学生的课业压力，基于此数学教师在作业设计方面还需要更多地利用相应的技巧对作业形式进行设计，如分层布置作业、设计特色作业等多方面从而确保学生可以有效开展学习，通过作业训练，使学生把握知识的能力和综合素养能得到更好的提升.

参考文献：

［1］ 谈言慧.提升初中数学课堂教学质量的策略研究［J］.新课程，2021（37）：68.

［2］ 陈福.优化课堂 激发学习——浅谈初中数学教学的有效策略［J］.数学学习与研究，2021（21）：20-21.

［3］ 王学男，赵江山.“双减”背景下作业设计的多维视野和优化策略［J］.天津师范大学学报（社会科学版），2022（2）：38-44.