自适应坡度的复合电源物流车能量管理研究*
吴婧之 余芳 杨佳珠 刘静雯 杨勇生
(上海海事大学,上海 201306)
主题词:复合电源 能量管理 道路坡度 模糊控制 粒子群优化
1 前言
在电动物流车的储能系统中,由超级电容和蓄电池并联组成的复合电源相较于单一锂离子电池电源能更有效地降低电池电量消耗、提升电池寿命,而在复合电源中,能量管理策略的合理性起着极其关键的作用。
目前,针对复合电源能量管理的研究主要可以分为基于规则的能量管理和基于优化的能量管理[1]。基于规则的能量管理采用预先设定规则的方式对能量进行分配,主要有逻辑门限控制[2]、模糊控制[3]和自适应控制[4]等。基于优化的能量管理采用智能优化算法优化电池或超级电容的功率分配参数,主要包括动态规划[5]、神经网络[6]和庞特里亚金极小值原理[7]等。
在当前的研究中,很少有文献考虑到路面坡度条件对能量分配策略的影响,但在长距离物流运输过程中,坡度变化往往是不可避免的。针对不同的坡度信息实施相应的功率分配,有助于进一步降低能量消耗量。鉴于此,本文提出一种自适应坡度的模糊控制策略,针对不同的坡度系数制定相应的模糊规则,并采用粒子群优化算法对该控制策略进行优化。
2 复合电源系统建模
2.1 复合电源拓扑结构
复合电源系统主要由蓄电池、超级电容、DC/DC 转换器、DC/AC 转换器和驱动电机组成,包含全主动式、半主动式和被动式3 种类型。其中,被动式结构成本低,但其效率不高,主动式结构精度高,但其控制难度高且成本高昂[1]。因此,综合考虑成本和控制效果,本文选择半主动式复合电源结构进行研究,其拓扑结构如图1所示。
在半主动式复合电源的拓扑结构中,锂电池和超级电容与双向DC/DC 转换器连接,通过双向DC/DC 转换器向直流母线提供直流电,直流电经DC/AC 转换器的电流逆变过程转换为交流电为驱动电机供电。
2.2 电动汽车复合能源系统的基本参数
以某厢式轻型载货物流车的参数与动力性能指标为参考,设置纯电动物流车的基本仿真参数如表1 所示。
2.3 复合电源系统模型
2.3.1 电池模型
本文中电池模型仅用于反映电池基本特性,没有高精度的要求,因此电池模型选用最基本的内阻模型,将电池等效为一个理想电压源和一个串联电阻,如图2所示。其中,Ubat为电池开路电压,Rbat为电池内阻,Ibat为流经电池的电流。

图2 电池模型等效电路
流经电池的电流为:
式中,Pbat为电池的消耗功率。
电池荷电状态(State Of Charge,SOC)Sbat为:
式中,Sbat_init为电池初始荷电状态;Cbat为电池容量。
2.3.2 超级电容模型
超级电容采用常规阻容(RC)模型,将超级电容等效为一个电容和一个串联电阻,等效电路如图3 所示。其中,Cuc为超级电容的电量,Uuc为超级电容的开路电压,Ruc为内阻,Iuc为流经超级电容的电流。

图3 超级电容模型等效电路
超级电容SOC可利用其电压定义为[1]:
2.3.3 DC/DC转换器模型
双向DC/DC 转换器的作用是通过电压调节实现动力电池与超级电容之间的功率分配[8]。DC/DC转换器的效率表达式为:
式中,ϑ为将动力电池与超级电容电压比作为变量的查表函数;Uc、Ic分别为DC/DC转换器的输出电压和电流。
3 自适应坡度的能量管理控制方法
本文采用半主动式复合电源拓扑结构,并针对该拓扑结构制定相应的能量管理控制方法。
3.1 复合电源的功率分配原理
将物流车视为一个质点,仅考虑车辆的纵向动力学模型,得到车辆需求功率为:
式中,v为车速;g为重力加速度;α为道路坡度角。
忽略系统功率损失,整车消耗的功率为:
式中,Puc为超级电容提供的功率。
则复合电源功率分配可表示为:
式中,Kuc为超级电容的功率分配因子。
3.2 道路坡度模型的建立
物流车行驶时,通过车载卫星定位系统(Global Positioning System,GPS)和地理信息系统(Geography Information System,GIS)采集前方坡度状况,并根据采集到的道路信息计算出道路坡度系数,如图4所示。其中,Δh为采样点与车辆当前位置之间的高度差,L为当前位置与采样点之间的直线距离[9]。

图4 道路坡度系数计算示意
道路坡度系数的计算公式为:
3.3 模糊控制器的基本结构
将车辆需求功率、超级电容SOC、蓄电池SOC 和道路坡度系数通过输入接口传递给模糊控制策略模块,经“模糊化-模糊推理-解模糊”后,得出超级电容的参考输出功率和蓄电池组的参考输出功率,基本结构如图5所示。

图5 模糊控制器基本结构
3.4 隶属度函数的设计
模糊控制器中常用的隶属度函数有三角形、钟形、梯形、高斯分布函数等,其隶属度函数越平滑,输出响应的速度越快[10]。因此,本文采用较为平滑的三角形和梯形隶属度函数组合设计模糊控制器,其输入、输出变量的论域与含义如表2所示,输入与输出的隶属度函数如图6所示。针对上坡、平路、下坡3种不同的坡度分别制定不同的模糊规则,上坡时调高超级电容功率分配因子,以满足车辆大功率需求,下坡时降低超级电容功率分配因子,使超级电容储存电量,如表3所示。

表2 隶属度函数的输入、输出变量论域与含义

表3 模糊控制规则
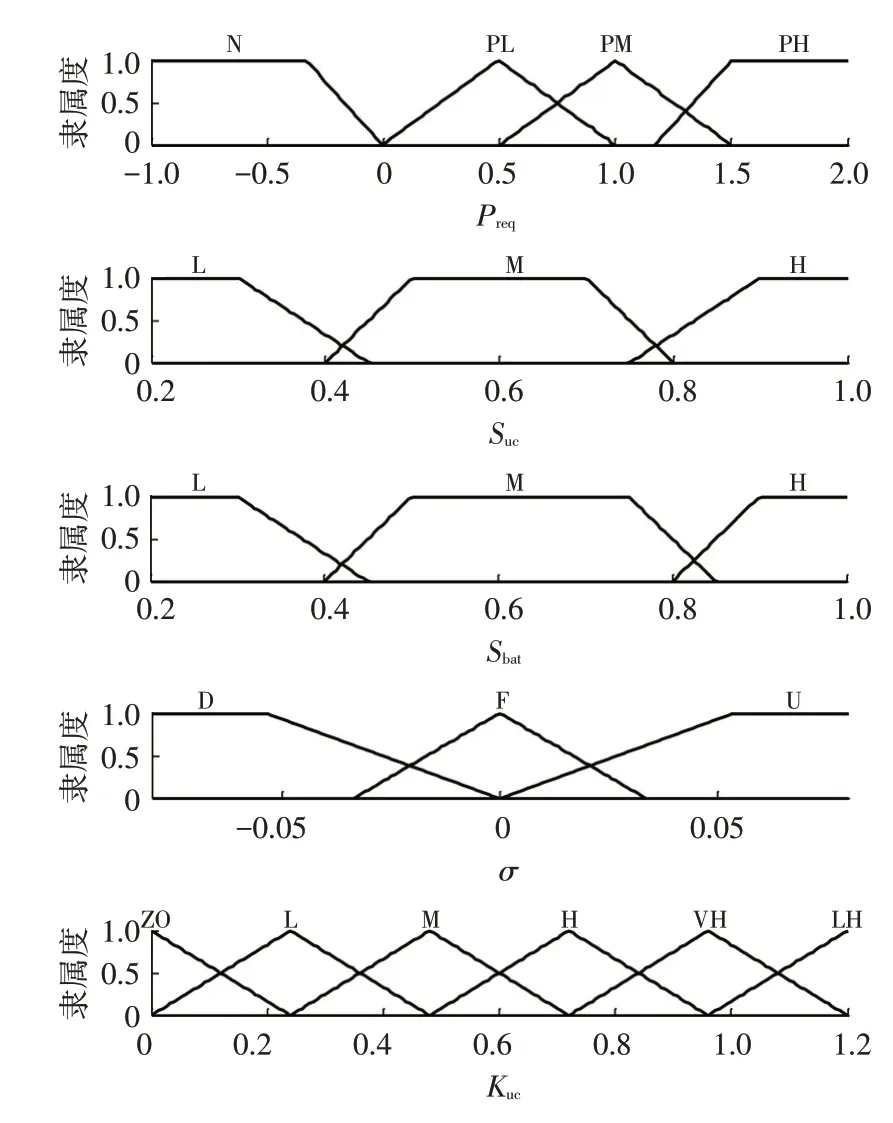
图6 输入与输出参数的隶属度函数
4 基于粒子群算法的模糊控制参数优化
4.1 待优化参数的设置
三角形、梯形隶属度函数分别由3 个和4 个待优化参数决定形状和位置,根据图6 所示的隶属度函数,待优化参数的设定如表4所示,其中,xij表示需求功率隶属度函数中第i个隶属度函数的第j个特征参数,yij、zij、aij、bij与xij同理。

表4 模糊控制器待优化参数
根据各模糊子集之间的关系,同时为缩短运算时长,设置优化参数需要满足的基本约束条件为:
式中,xmin、ymin、zmin、amin、bmin分别为隶属度函数形状约束的下限;xmax、ymax、zmax、amax、bmax分别为隶属度函数形状约束的上限。
4.2 适应度函数的选取
本文复合电源能量管理策略的设计目的为在保证车辆动力性的前提下,通过合理分配需求功率,实现整车耗电量最小。因此,将适应度函数ffitness定义为:
式中,Eess为整车总能耗;s为车辆行驶的总里程;t0、t1分别为车辆运行的起始和终止时刻。
4.3 粒子群优化的原理及流程
粒子群优化(Particle Swarm Optimization,PSO)算法具有易实现、精度高等优点,与其他智能算法相比,可达到更优的调参效果[11]。因此,本文选取PSO算法对模糊控制隶属度函数的待优化参数进行优化。算法速度更新和位置更新公式分别为[12]:
式中:vid(k)、xid(k)分别为粒子群中第i个粒子第k次迭代的速度和位置的第d维分量;w为用来平衡全局与局部搜索能力的惯性权重;Pbest、gbest分别为全局和局部粒子的最佳位置;nrand为(0,1)范围内的任意数;c1、c2分别为用于调节向全局最优粒子和个体最优粒子飞行方向最大步长的学习因子。
用粒子群优化算法对隶属度函数的待优化参数进行优化的流程如图7所示。

图7 粒子群优化流程
5 仿真结果分析
基于MATLAB/Simulink 环境搭建复合电源物流车模型,选取CYC_UDDS 作为仿真工况,该工况下的最高车速为91.2 km/h,运行时间为1 370 s,空载时间为259 s,停车次数为17次。车速随时间的变化如图8所示。

图8 CYC_UDDS工况车速曲线
采用本文所提出的控制策略对复合电源物流车能量管理过程进行仿真,由3个场景组成:场景1和场景2为分别固定上坡坡度和固定下坡坡度场景,仅用于测试该策略在上坡工况和下坡工况的表现;场景3采用针对我国实际道路情况而制定的包含上下坡的城市道路坡度,具有实际意义。对于场景1 和场景2,由于在同时符合城市道路设计规范行业标准[13]和保证汽车动力性的前提下所允许的最大道路坡度系数为5%,因而选择±5%作为固定上坡和固定下坡的道路坡度系数。3个场景下均采用了模糊控制、自适应坡度的模糊控制和自适应坡度的模糊控制结合粒子群优化3种控制策略,并分别对电池电量消耗、电池电流波动情况以及整车总能耗进行对比分析。
5.1 上坡仿真结果分析
上坡场景下电池SOC 仿真结果如图9 所示。相较于未考虑坡度的模糊控制,自适应坡度的模糊控制使电池SOC 降低了2.53百分点,粒子群优化后,电池的耗电量相较于未考虑坡度的模糊控制降低了3.66 百分点。因而所提出的控制策略能够提高超级电容的利用率,从而达到降低电池电量消耗,增加续航里程的目的。

图9 上坡场景下电池电量消耗结果
模糊控制下,电池的平均电流为51.87 A,自适应坡度的模糊控制下,平均电流为50.19 A,经粒子群优化算法优化后,平均电流为49.45 A,如图10 所示。随着控制策略的改进,平均电流逐步下降,更低的平均电流说明功率分配策略更加合理,使得超级电容承担了一部分需求电流,从而有效降低了蓄电池的工作负荷,有利于延长电池循环寿命,起到保护电池的作用。

图10 上坡场景下电池电流波动情况
模糊控制下物流车总能耗为2 090.09 kJ,自适应坡度的模糊控制下物流车总能耗为2 028.14 kJ,粒子群优化结合自适应坡度的模糊控制下物流车总能耗为2 017.46 kJ。相较于普通模糊控制,后两者分别减少2.96%、3.47%的能量消耗。这说明在制动工况下,超级电容回收制动能量的效率提高了,能够回收更多的电量加以重复利用,提升了电动物流车的经济性。
5.2 下坡仿真结果分析
考虑到下坡时所采取的控制策略目的是使超级电容优先回收制动能量,而动力电池次之,且下坡时所消耗的功率较小,因此,调低超级电容的基准输出功率,将动力电池作为主要能量来源,使动力电池的耗电量和波动电流相比于优化前略有升高。下坡场景下电池SOC和电流波动情况仿真结果如图11所示。未考虑坡度的模糊控制下电池平均电流波动为0.69 A;自适应坡度的模糊控制下电池平均电流波动为0.88 A;粒子群优化后,电池平均电流波动为1.01 A。虽然优化后,电池的耗电量和电池电流升高了,但在电池耗电量和电流波动的差距不大,对电池基本不造成影响的情况下,整车能耗明显降低,且超级电容储存了更多的电量,如图12所示。

图11 下坡场景下电池电量消耗和电流波动情况
模糊控制下物流车总能耗为643.91 kJ;自适应坡度的模糊控制下物流车总能耗为472.03 kJ;粒子群优化后,总能耗为457.74 kJ。下坡时车辆会产生大量的再生制动能量,此时若能够有效回收并加以利用,将能大幅降低整车能耗。相较于模糊控制,自适应坡度模糊控制和结合粒子群优化算法的自适应坡度模糊控制分别减少了26.69%、28.91%的能量消耗,说明超级电容回收了更多的再生制动能量,大幅提高了物流车的经济性。
下坡场景下超级电容SOC 变化情况如图12 所示。经坡度优化后,超级电容多储存了8.77百分点的电量,再用粒子群优化后,超级电容多储存了14.02 百分点的电量,能够有效避免在大功率放电条件下因超级电容电量不足而导致电池作为单一电源单独供电,从而延长电池寿命。

图12 下坡超级电容电量消耗情况
5.3 混合道路坡度仿真结果分析
结合城市道路设计规范行业标准的要求[13],设置道路坡度随时间的变化如图13所示,对车辆进行仿真。

图13 混合道路坡度场景道路坡度变化情况
混合道路坡度场景下的仿真结果如图14 所示,具体数据对比结果如表5 所示。可以看出在本文所提出的控制策略下,电池消耗的电量、电池电流波动以及整车总能耗都有一定程度降低,可有效提高续驶里程,延长动力电池使用寿命,超级电容能更好地回收制动能量,从而提高车辆的经济性。

图14 混合道路坡度场景下的物流车仿真结果
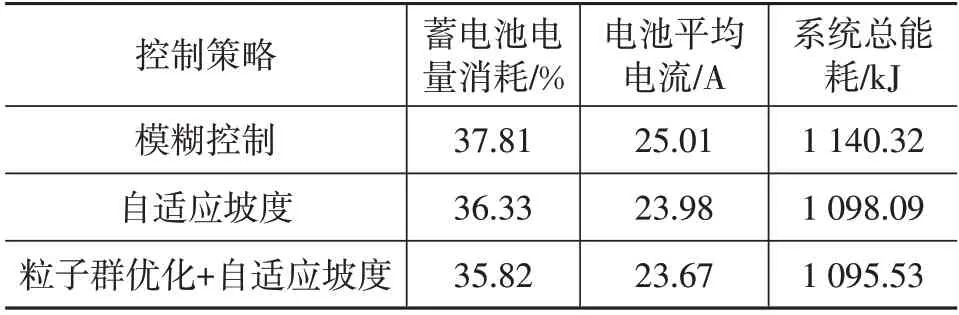
表5 混合道路坡度场景下3种策略求解结果对比
6 结束语
本文针对复合电源物流车能量管理问题,提出了一种自适应坡度的模糊控制结合粒子群优化的能量管理策略。对比优化前、后的仿真结果表明,相较于未考虑坡度的模糊控制,物流车在自适应坡度的模糊控制下,能够发挥超级电容和电池各自的优势,实现更合理的功率分配。因此,本文所提出的控制策略在保证整车动力性的前提下,使复合电源能量实现了更合理分配,进一步提升了车辆的经济性。

