基于柔性演员-评论家算法的自适应巡航控制研究*
赵克刚 石翠铎 梁志豪 李梓棋 王玉龙
(1.华南理工大学,广州 510641;2.湖南大学,汽车车身先进设计制造国家重点实验室,长沙 410082)
主题词:自适应巡航控制 柔性演员-评论家 可迁移性 深度强化学习
1 前言
自适应巡航控制(Adaptive Cruise Control,ACC)是重要的自动驾驶辅助技术,而目前的ACC 算法依赖于大量的标定工作,并且存在复杂环境下适应性差、表现不佳的问题[1-2]。深度强化学习(Deep Reinforcement Learning,DRL)通过智能体与环境交互进行自学习最大化累计奖励值,以学习到目标任务的最优策略[3-5],在未来有望解决自动驾驶等复杂系统的控制决策问题,已经在路径规划[6-7]、轨迹跟踪[8-9]和跟驰控制[10-11]等自动驾驶领域得到了较为广泛的研究。针对ACC算法适应复杂工况能力差的弊端,DRL可以提供新的研究思路。
目前,在自动驾驶领域应用的DRL 算法主要为无模型的确定性策略和随机性策略。在确定性策略算法研究中:Fu 等[12]利用深度确定性策略梯度(Deep Deterministic Policy Gradient,DDPG)算法训练紧急制动决策策略,可提高安全性;Qian 等[13]利用双延迟深度确定性策略梯度(Twin Delayed Deep Deterministic Policy Gradient,TD3)算法并考虑拓扑路径的特点训练自动驾驶决策策略,解决行为决策与轨迹规划的一致性问题。上述文献所使用的确定性策略算法在训练过程中虽然能够较快地收敛到稳定状态,但是环境探索不充分且可能得到局部最优策略的缺点,使得模型的迁移性和泛化能力较差。
针对确定性策略算法探索能力差的问题,随机性策略框架提供了更全面的环境探索。Liu等[14]使用异步优势演员-评论家(Asynchronous Advantage Actor-Critic,A3C)算法并考虑节能因素,提出一种自动驾驶决策策略;He等[15]采用近端策略优化(Proximal Policy Optimization,PPO)算法提出一种自动驾驶多目标纵向决策方法,并通过熵约束加快模型训练,提高算法的稳定性。以上文献采用的随机性策略算法探索能力更强,有更好的环境适应能力,但使用的是在线策略,对历史样本数据利用率低。
因此,本文提出一种基于柔性演员-评论家(Soft Actor-Critic,SAC)的ACC 算法。建立车辆自适应巡航的马尔可夫决策过程,构建合理的演员和评论家网络并加入自调节温度系数,通过设计模块化奖励函数以及新的样本训练模式进一步优化算法。将所提出的控制算法在不同仿真环境和实车环境中进行测试,验证算法的有效性。
2 自适应巡航车辆数学模型
2.1 车辆跟随模型
本文以乘用车为研究对象,车辆自适应巡航场景如图1所示。

图1 车辆自适应巡航场景示意
主车跟随目标车行驶过程中,目标距离作为自适应巡航控制的重要指标,在保证行车安全和道路交通效率的同时还需兼顾驾驶员的心理预期。本文采用可变安全距离策略中的固定车头时距(Constant Time Headway,CTH)[16]作为目标距离的计算方法。车头时距τh定义为:
式中,d为主车与目标车的实际距离;v为主车速度。
将τh设置为固定值,则采用CTH 计算的目标距离dgoal为:
式中,d0为目标车静止时与主车的最小安全距离。
2.2 马尔可夫决策过程
将主车作为DRL 的智能体,其跟随目标车的行驶过程使用马尔可夫决策过程(Markov Decision Process,MDP)表示。MDP 由4 维数组[S,A,P,R]描述,其中,S、A分别为状态空间和动作空间,P为状态转移概率,R为奖励函数。本文将t时刻主车与目标车的实际距离与目标距离间的误差Δdt,主车实际速度与目标速度(即目标车速度)的误差Δvt作为状态输入,t时刻主车的目标速度vgoalt作为动作输出,定义t时刻的状态空间st和动作空间at为:
式中,ΔDL、ΔDH分别为距离误差的下限与上限;ΔVmin、ΔVmax分别为速度误差的最小值与最大值;Vmin、Vmax分别为目标速度的最小值与最大值。
t时刻自适应巡航的控制过程可以描述为:智能体接收到状态信息st,执行DRL 产生的动作at,通过奖励函数R获得奖励值,并根据状态转移概率P将状态转移至st+1。
3 自适应巡航的DRL控制算法
3.1 算法结构
本文在柔性Q学习(Soft Q-Learning,SQL)[17]基础上改进获得一种基于最大熵原理的DRL 算法,其通过离线策略的方法优化一个随机性策略,在连续动作空间的复杂系统中具有较好的适用性。如图2 所示为基于该算法的自适应巡航DRL 过程,其学习目标是找到累计奖励与熵的和期望最大的策略π*:
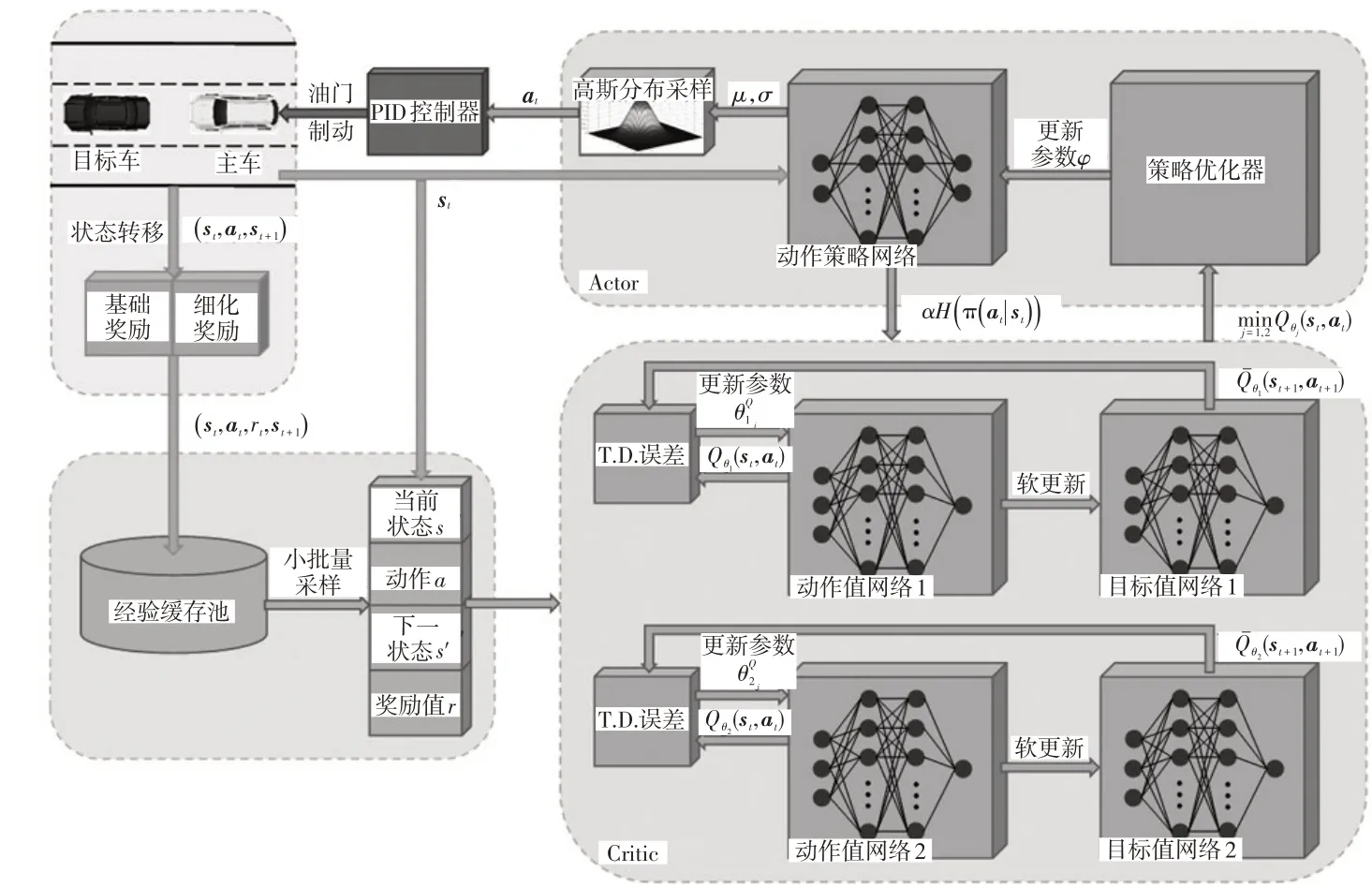
图2 自适应巡航控制DRL过程
式中,E(st,at)~π为期望;r(st,at)为t时刻ACC 系统采取控制动作的奖励;H(π(·|st))=-Eα[log(π(at|st))]为在策略π下动作的熵;α为温度系数,决定熵相对于奖励的权重。
本文使用深度神经网络拟合动作值函数和动作策略函数,分别组成评论家(Critic)和演员(Actor)网络。
3.1.1 评论家网络
对于动作值函数,使用2层隐藏层的全连接层网络对其进行拟合。在如图3所示的动作值网络中,以状态st和动作at作为输入,线性整流函数(Rectified Linear Unit,ReLU)f(x)=max(0,x)作为激活函数,at的估计值作为输出。

图3 动作值网络
动作值网络的损失函数为动作值函数Qθ(st,at)和动作值目标函数的均方差:
其中:
式中,θ为动作值网络参数;γ为折扣因子。
具体训练中,使用双动作值网络并选取最小的Qθ(st,at),以减少对动作值的高估。
3.1.2 演员网络
与动作值函数的拟合相同,动作策略函数同样使用2 层隐藏层的全连接层网络进行拟合。如图4 所示的动作策略网络中,以状态st作为输入,ReLU 作为激活函数,高斯分布的均值μ和方差σ作为输出。但由于μ和σ采样动作并不可导,无法计算损失函数的梯度。因此,本文采用重参数的方法,将反向传播路径中的高斯分布用标准正态分布代替,从标准正态分布中获取采样值εt,从而获得对应均值和方差高斯分布的采样动作at:

图4 动作策略网络
动作策略网络的损失函数为网络估计的高斯分布与实际基于能量分布的期望KL 散度(Kullback-Leibler Divergense):
式中,φ为动作策略网络参数;DKL为KL散度;Zθ(st)为使分布正则化的配分函数。
另外,高斯分布中采样得到的动作at的值域为(-∞,+∞),但在自适应巡航场景中速度作为动作是有界的,因此需要对动作at进行变换。本文使用压缩高斯分布,将at用tanh激活函数处理,将其值域映射到(-1,+1);然后进行换元计算,将激活值乘以自适应巡航限制的最高速度得到真实目标速度vgoal。
3.2 自调节温度系数
车辆在自适应巡航时,温度系数α作为熵的权重,起到控制策略随机性的作用。α越大,则控制策略越随机,ACC 系统对环境的探索越充分,即会尝试更多的动作。文献[18]使用依赖先验的固定α,但由于奖励值不断变化,采用固定α会导致训练不稳定,且容易收敛到局部最优。因此,本文设计自调节温度系数α,即当ACC 系统探索到新的区域时,最优动作未知,将α调大鼓励探索更多动作空间,当某一区域探索比较充分时,最优动作基本确定,将α适当减小。
t时刻最优温度系数为:
式中,αt为t时刻的温度系数;H为当前状态采用动作的熵。
温度系数的损失函数为:
式中,H0为熵的阈值。
3.3 奖励函数
奖励函数是DRL 的重要部分,对训练效果有直接的影响,好的奖励函数可以引导智能体快速学习到有用的知识,加快训练效率、提高训练效果。本文设计的奖励函数分为基础奖励和细化奖励。
3.3.1 基础奖励
基础奖励的作用是为智能体确立学习的基础目标和具备的基本功能,其产生于训练的每一个时间步。考虑到自适应巡航汽车实现基本跟车功能的同时需兼顾乘坐舒适性,因此设计的基础奖励rb由状态量与纵向加速度构成[19]:
式中,a为纵向加速度;ξ1、ξ2、ξ3为基础奖励各变量的权重系数,权重系数越大,训练过程中越重视该变量,本文自适应巡航DRL 控制过程侧重于更快地缩小距离误差,因此确定ξ1=8、ξ2=2、ξ3=1。
基础奖励的分布如图5所示。

图5 基础奖励分布
3.3.2 细化奖励
为了解决奖励稀疏的问题,防止智能体学习缓慢甚至无法学习的情况出现,本文运用奖励塑造(Reward Shaping)的思想[20]设计细化奖励。如图6 所示,其分为过程奖励、安全奖励和完成奖励。
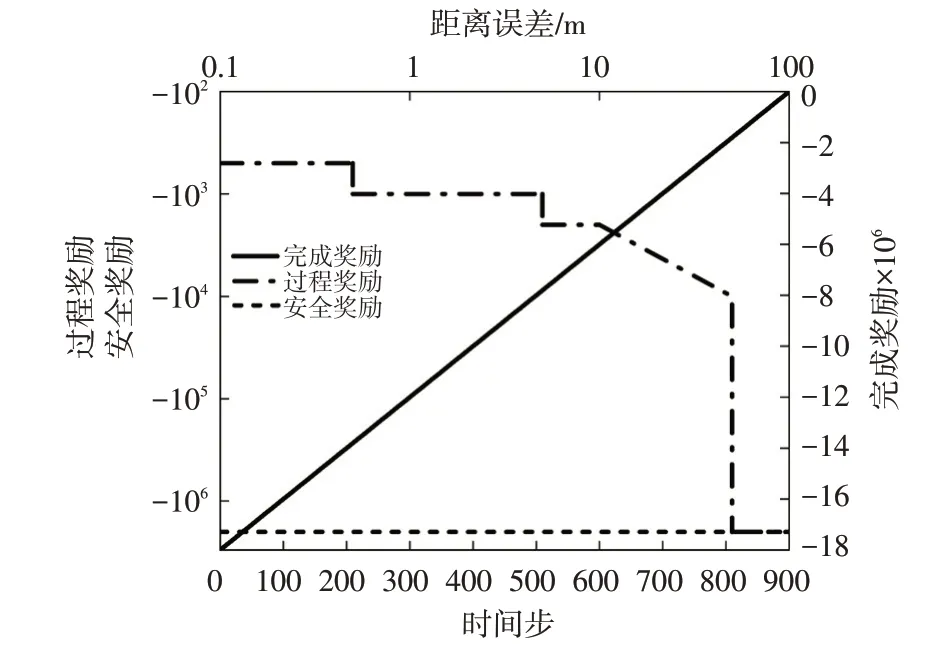
图6 细化奖励函数
过程奖励可以使智能体在训练过程中尽可能减小距离误差,其产生在训练的每一个时间步。距离误差越大,智能体获得的过程奖励越小;当距离误差超过50 m时,给予智能体最小的过程奖励并使训练终止,过程奖励rp的表达式为:
安全奖励rs的作用是防止主车与目标车发生碰撞,其产生于两车发生碰撞训练终止时:
完成奖励ra的作用是促进智能体完整地执行自适应巡航任务。当主车走完一个回合(900个时间步)时,ra=0,当主车与目标车碰撞或|Δd|>50 m导致训练终止时,有:
式中,k为一个训练回合里已经走过的时间步。
3.3.3 奖励缩聚因子
在训练过程中,自适应巡航场景的环境随机因素较多,因此状态之间的差别较大,可能使得动作值网络参数变化剧烈,导致神经网络收敛变缓,甚至发散。为避免这一现象,本文在训练过程中对奖励赋予缩聚因子χ,使样本梯度的绝对数量级减小,从而使神经网络的训练更稳定。因此,集成的总奖励r为:
3.4 经验回放机制
本文提出的算法使用离线策略,引入经验缓存池储存智能体与环境交互产生的经验数据,从中随机抽取小批量样本用于训练动作值网络。经验缓存池保存数据的格式为四元数组(st,at,st+1,rt),即智能体与环境交互产生的当前所处的状态、当前产生的动作、下一时刻所处的状态和当前产生的奖励值。
传统的经验回放机制中,随着训练的进行,经验缓存池逐渐增大,但放入新数据的频次不变,导致缓存池中新数据的比例减少,使得训练的效果变差。针对这一问题,本文提出一种新的样本训练模式,即按照经验缓存池的大小改变模型的训练次数,随着新数据比例的下降,训练次数也逐渐增加。具体步骤为:
a.定义经验缓存池最大容量Cmax。
b.训练过程产生的经验数据逐组放入缓存池。
c.当缓存池C的范围为0.01Cmax≤C<0.1Cmax时,每增加100组新数据,训练智能体20次且每次小批量采样大小为的数据;当0.1Cmax≤C<Cmax时,每增加100组新数据,训练智能体30 次且每次小批量采样大小为的数据;当C=Cmax,即达到最大容量时,每进行100 个时间步,训练智能体40 次且每次小批量采样大小为的数据。
4 仿真与分析
4.1 训练场景设计
本文通过Python 与LGSVL 自动驾驶仿真器进行联合仿真训练。为了减小仿真训练得到的控制算法应用到实车中的误差,本文在训练中使用与实车上参数相近的激光雷达与轮速传感器获取状态信息。设计训练场景为τh=3 s、d0=10 m[16]。仿真时,主车与目标车在同向两车道、每条车道宽为3.5 m 的一条直道上行驶。主车与目标车都以10 m/s的初始速度行驶,两车的初始距离为10 m。目标车行驶工况如图7所示。
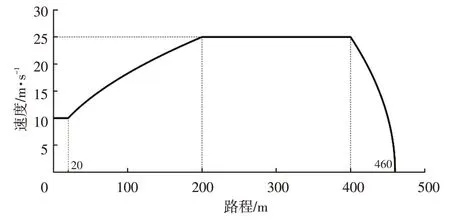
图7 目标车行驶工况
4.2 DRL模型训练
模型训练在Windows10 操作系统下进行,内存为64 GB,处理器为Intel 酷睿i7-8700K,显卡为NVIDIA GeForce RTX 2080 Ti,利用深度学习框架PyTorch。
本文算法的超参数对训练效果的影响:折扣因子γ用来计算累计奖励,γ越大越肯定以往的训练效果,γ越小越肯定当前回报;批量大小越大,训练的精度越高,但过多将使神经网络梯度变化减缓,从而无法走出局部最优点;神经网络学习率lr过大,在梯度下降时网络参数变化过大,会使神经网络无法收敛,lr过小,网络参数变化过于缓慢,会使神经网络学不到有效的知识。经多次训练试验,确定较优的算法超参数如表1所示。

表1 算法超参数
图8所示为训练累计奖励变化的结果,由图8可以看出,与采用相同奖励函数的基于DDPG的ACC算法相比,本文提出的基于SAC的控制算法获得的最高奖励相近,取得最高奖励的时间变长。主要原因为:本文算法采用随机性策略,在训练过程中探索更全面充分,可以学习到最优和次优策略,所以奖励曲线的波动较大、训练时间较长;DDPG算法采用确定性策略,对环境的探索不足,只能学习到最优策略,因此较快地达到最高奖励。

图8 DRL模型训练结果
4.3 标准测试场景仿真验证
为验证本文算法的有效性和鲁棒性,选取自适应巡航标准测试场景中的目标车静止、低速和减速试验场景进行仿真验证。设定主车与目标车的初始距离为250 m,主车最高车速30 m/s,对每一个试验场景测试30回合并取数据平均值。规定标准测试场景下距离误差和速度误差分别收敛到0.8 m和0.3 m/s即认为达到自适应巡航稳定状态。
4.3.1 目标车静止场景
在目标车静止场景中,主车分别以初始速度为测试场景规定最低速30 km/h 与最高速60 km/h 的工况行驶。如图9所示为目标车静止场景下的主车状态曲线,从图9 中可以看出,SAC和DDPG 控制算法都采取了先加速缩短距离误差、后减速缩小速度误差的控制策略,以提高自适应巡航控制的效率,加快达到稳定状态。在主车初始速度为30 km/h的工况下,使用SAC和DDPG控制算法的最高速度分别为24.705 4 m/s 和26.040 3 m/s;在主车初始速度为60 km/h的工况下,使用SAC和DDPG控制算法的最高速度分别为26.064 9 m/s和27.129 2 m/s。2种工况下SAC控制算法与DDPG相比最高速度分别降低了5.13%和3.92%,SAC 控制算法在速度安全性上较DDPG有所提高。

图9 目标车静止场景下主车的状态曲线
4.3.2 目标车低速场景
在目标车低速场景中,主车分别以初始速度为测试场景规定最低速80 km/h 与最高速120 km/h 的工况行驶,目标车以30 km/h的速度行驶。如图10所示为目标车低速场景下的主车状态曲线,从图10中可以看出,在主车初始速度为80 km/h 的工况下,初始速度未超过最高车速30 m/s,因此SAC 和DDPG 控制算法都采取了先加速后减速的控制策略;在主车初始速度为120 km/h的工况下,初始速度超过最高车速,因此2 种控制算法都先减速到最高车速,随后保持最高车速匀速行驶来加快减小距离误差,其中DDPG控制算法保持最高车速到第117个时间步后减速,SAC 控制算法保持最高车速到第29个时间步后减速,后者保持最高车速的时间更短,具有更好的速度安全性。因此,该场景下SAC控制算法相比于DDPG采取的是更保守的控制策略。

图10 目标车低速场景下主车的状态曲线
4.3.3 目标车减速场景
在目标车减速场景中,主车以120 km/h 的初始速度行驶,目标车以70 km/h 的初始速度、2 m/s2的减速度行驶。如图11a 所示,SAC 控制算法的距离误差最值较DDPG 控制算法大,主要原因为SAC 控制算法在跟车过程中倾向于增大距离误差来加快缩短速度误差,这与设置的奖励函数权重系数有关。图11b 中速度误差曲线出现锯齿形状的原因为LGSVL 仿真软件无法设置目标车匀减速行驶,因此人为对匀减速过程进行差分。如图11c 所示,2 种算法都采取减速的控制策略,由于主车初始速度高于最高车速,因此2 种控制算法都在仿真初期短时间内将速度减小到最高车速,其中DDPG 控制算法会保持最高车速行驶一段时间再减速到稳定状态,而SAC 控制算法继续减速收敛到稳定状态。

图11 目标车减速场景下主车的状态曲线
4.3.4 仿真结果总体分析
在3 种场景的5 个工况下,对于距离误差,2 种算法收敛至稳定状态所用的时间基本相同;而对于速度误差,如表2所示,SAC控制算法相比于DDPG收敛至稳定状态所用的时间分别减少了19.02%、22.32%、13.20%、16.97%、19.64%,明显提高了自适应巡航的控制效率。

表2 不同场景下速度误差收敛至稳定状态所用的时间步
另外,冲击度(加速度对时间的一阶导数)反映了车辆在行驶过程中由于加、减速产生抖动颠簸的程度,可以作为乘坐舒适性的衡量指标。如表3 所示,SAC控制算法的冲击度(绝对值)的均值较DDPG 分别减小了25.20%、18.77%、23.92%、4.98%、46.22%,最值分别减小了57.09%、46.83%、75.20%、38.35%、57.07%,使主车行驶过程更加平稳,提高了乘员乘坐的舒适性。

表3 不同场景下主车冲击度(绝对值)均值和最值
从仿真结果可以看出,本文算法能够完成标准测试场景的仿真验证,与DDPG控制算法相比具有更好的速度安全性、控制效率和乘坐舒适性,对训练场景外的环境具有更好的泛化能力。
5 实车试验
为检验本文所提出的算法迁移到实车中的自适应巡航控制效果,如图12所示,在广州市番禺区内的一条长度为600 m的近似直道上进行相关测试。如图13所示,试验场景包括主车和目标车2辆车。试验主车由某品牌纯电动汽车线控改装获得,搭载激光雷达检测目标车的相对距离和速度,并利用轮速传感器获取自身速度信息。

图12 试验路线

图13 试验主车和场景示意
试验过程中,为提高场景的真实性及复杂度,主车与目标车的初始距离随机确定。具体工况为:主车与目标车均从静止起步,目标车按照驾驶员的驾驶习惯从静止加速到40 km/h,并在该速度附近沿道路行驶。
图14 所示为实车试验主车状态曲线,从图14a、图14b中可以看出,使用SAC控制算法的距离误差在经过起步阶段的超调后可以迅速缩小到5 m 内,而使用DDPG控制算法的距离误差超调时间较长,且超调时最大误差超过30 m。由图14c、图14d 可以看出,使用DDPG 控制算法时速度误差波动较大,幅值超过6 m/s,而使用SAC 控制算法可以保持更小的速度误差。图14g、图14h中,使用SAC控制算法的冲击度(绝对值)明显小于DDPG,在乘车体验上更为舒适。在实车试验中,虽然存在信息传递延迟和丢包、激光雷达误检测等情况,但SAC控制算法并没有使主车出现状态急变,能够稳定地跟随目标车行驶,在实车上有较好的表现效果。

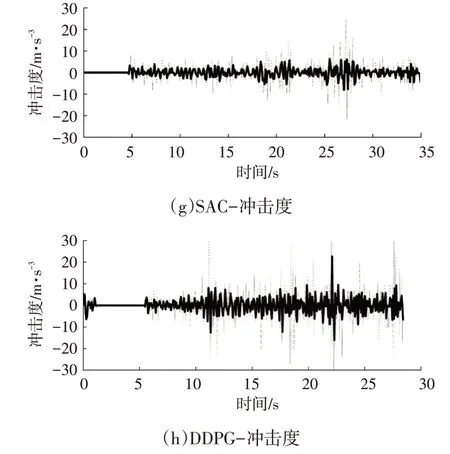
图14 试验主车状态曲线
6 结束语
本文研究了DRL算法在自适应巡航控制技术中的应用问题,提出一种基于SAC的控制算法。将车辆自适应巡航的学习过程描述为马尔可夫决策过程,构建评论家和演员网络拟合动作值函数和动作策略函数;使用自调节温度系数改善智能体的探索效果;构建模块化奖励函数,改善了智能体的学习效率和效果,解决了奖励稀疏的问题;提出一种新的样本训练模式,按照经验缓存池的大小改变模型的训练次数,可以进一步提高样本的利用率。
试验结果表明,相比于DDPG 控制算法,本文所提出的算法能以更高的控制效率缩小速度误差,且冲击度(绝对值)更小,舒适性和安全性更好,在实车上的迁移性较好。在后续的研究中,将开展实车高速试验进一步检验算法的实车性能,并考虑路径跟踪、横纵向协同控制等自动驾驶场景的DRL控制问题。

