基于关键节点的改进A*无人车路径规划算法

张辉 张瑞亮,2 许小庆 范政武,2

（1.太原理工大学，太原 030024；2.山西省汽车设计工程技术研究中心，太原 030024）

1 前言

无人车系统主要包括感知、决策、规划和控制4 个模块[1]，其中规划模块负责基于目标任务生成最优路径。按照搜索方式可将路径规划算法分为基于图搜索、基于采样及基于人工智能的方法。其中，基于图搜索的A*算法因其寻优能力强、场景适应度高等特性而得到广泛应用[2]。

陈若男等[3]结合距离及角度信息改进传统A*算法代价函数，设计邻域选择策略，提升了算法效率和路径安全性。杨瑶等[4]通过改进距离估算方式，引入车身轮廓代价和障碍物距离代价，提升了A*算法规划效率和路径安全性。冯来春等[5]将A*算法和快速搜索随机树（Rapid-Exploring Random Tree，RRT）算法结合，降低了RRT 算法的采样盲目性。孟珠李等[6]将A*算法与B 样条曲线结合，改善了A*算法规划路径的平滑性。余文凯等[7]采用K-均值（K-Means）聚类算法对地图进行预处理，量化不同区域地图复杂度，依据复杂度设置搜索权重，应用弗洛伊德（Floyd）算法对路径进行平滑，提高了路径规划效率和路径平滑性。祁玄玄等[8]从目标性拓展等多个方面对传统A*算法进行改进，提升了A*算法的搜索效率。Frantisek等[9]研究了各种改进A*算法，如跳点搜索（Jump Points Search，JPS）、Phi*等，并基于部分算法进行了仿真验证。Hao等[10]提出了一种可以自适应调整搜索深度的Cell A*算法，使高复杂度场景地图下的计算耗时进一步缩短。Zahra等[11]在A*算法中引入动态可变栅格，增加了危险惩罚代价，提升了路径安全性和计算效率。

搜索效率和路径安全性及可行性是规划算法的核心，但A*算法多循环判断机制导致其路径性能和计算效率难以同时得到有效改善。因此，本文提出一种改进A*算法，基于地图预览模块提取栅格地图关键节点，规划模块依据关键节点信息判断是否开启增量式扩展搜索，引入基于安全距离的碰撞场模型改进代价函数，应用准均匀三次B 样条曲线对生成路径进行平滑处理得到最终的规划路径。最后与对比算法在不同复杂度场景下进行仿真验证。

2 传统A*算法

传统A*算法融合了广度优先搜索（Breadth First Search，BFS）算法和深度优先搜索（Depth First Search，DFS）算法的优势[3]，其基于当前节点与起点和目标点之间的距离信息进行节点扩展和选择。传统A*算法作为典型图搜索算法，其规划地图通常以栅格地图形式表达，如图1所示为某栅格地图示例。栅格地图尺寸决定了地图表达的精度和规模[12]，广义栅格地图仅包含障碍物信息。

图1 栅格地图

如图1所示，在规划过程中，车辆从起点出发，通过扩展循环最终行驶至目标点，传统A*算法具体流程如图2所示。

图2 传统A*算法流程

节点扩展时依据场景特点及无人车运动学特性选取四邻域方式进行节点扩展；代价函数f(N)通过当前节点与起始点间的真实距离g(N)和当前节点与目标节点间的预估距离h(N)累加得到[13-16]，h(N)一般采用曼哈顿（Manhattan）、欧几里得（Euclidean）、切比雪夫（Chebyshev）距离。

3 改进A*算法

传统A*算法存在搜索路径多曲折、紧贴障碍物边缘、不平滑及搜索时间随栅格地图规模增大而呈现指数型增长趋势等缺陷。一般结构化道路作为车辆的主要应用场景，其特点为道路多正向直行区间、多交叉区域、空间障碍物类型较多，因此其规划的路径无法直接适应无人车在此类环境下的工作需求。本文针对此类场景需求提出改进A*算法，流程如图3所示。

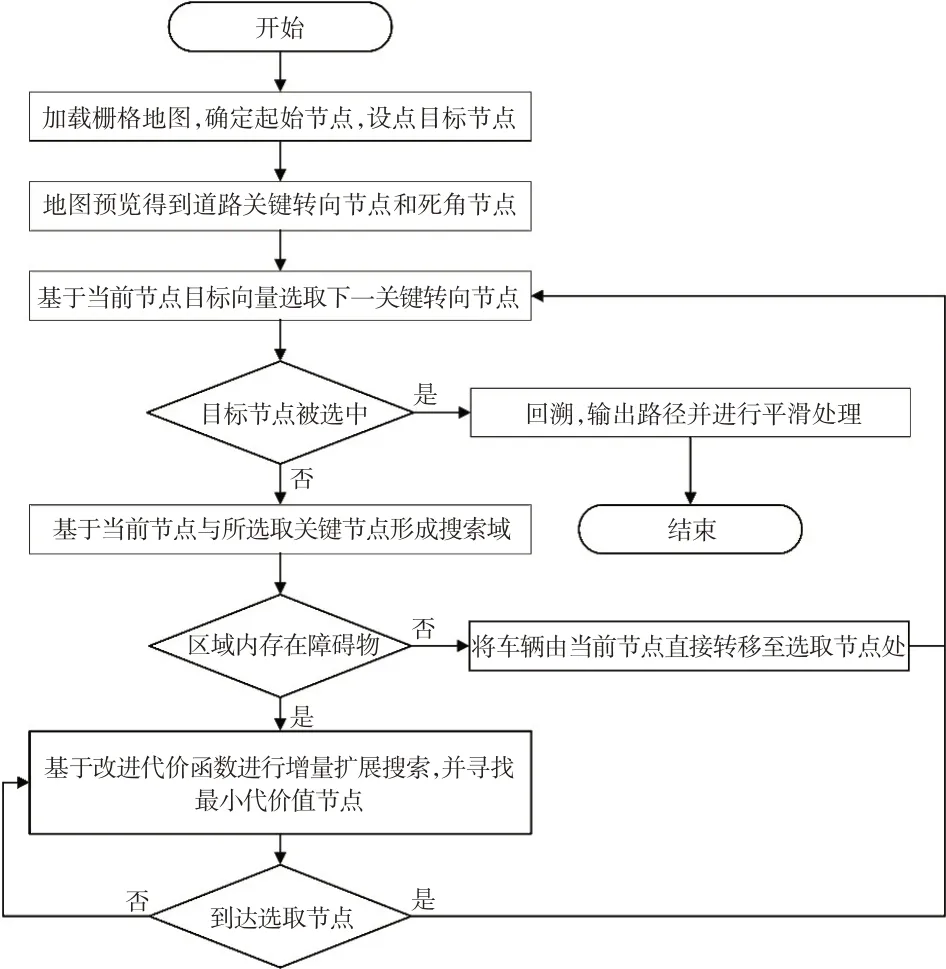
图3 改进A*算法流程

相对于传统A*算法，算法的主要改进如下：

a.引入地图预览模块提取道路转向关键节点和道路死角关键节点，并基于目标向量信息选取关键节点，基于当前节点和拟选择关键节点形成搜索域，基于障碍物判定规则判断是否开启增量式扩展搜索；

b.对不同类型障碍物进行分类，提出一种基于安全距离的碰撞场模型，并结合其对传统A*算法代价函数进行改进；

c.应用准均匀三次B 样条曲线对规划路径在转折处进行平滑，生成满足车辆运动学约束的最终路径。

3.1 基于关键节点信息的扩展搜索策略

3.1.1 关键节点信息获取

传统栅格地图作为地理信息载体[17]，其将环境抽象为栅格状态，仅反映不同位置障碍物信息。为进一步提高算法效率，本文提出一种基于地图预览模块获取栅格地图关键节点的方式。

获取栅格地图后，地图预览模块从栅格群中提取关键节点至关键节点列表中，并将道路边界节点集合提取至道路边界节点列表中。其中，关键节点包括道路转向关键节点和道路死角节点两类，分别存放于关键节点列表的不同列中，两类节点见图1，其中，道路死角关键节点仅能作为起点位置，一旦规划过程拟选定道路死角关键节点，则放弃该操作，重新进行节点选择。

3.1.2 目标向量定义

无人车在进行节点选择时，依据当前节点与目标点间向量，即目标向量进行判断，选取策略如图4所示，其中，S节点为起点，A、B、C、D节点为车辆可选关键节点，G节点为目标点。车辆从起点S出发，并基于当前位置的向量SG（当车辆行驶至新位置时，目标向量由当前节点与目标点构成）选择方向趋近于目标点的关键节点，判定拟选定的关键节点是否为道路死角关键节点，如果是，则放弃此节点，重新选择其他可行节点，反之，判断当前节点至拟选定节点间搜索域内是否存在障碍物，如果不存在，则直接将车辆从当前位置节点移至拟选定关键节点处，如果存在，则进行增量式扩展，得到该区域内无碰撞的安全路径。当车辆驶至拟选定关键节点后，依据直行优先原则，结合当前节点至目标节点向量进行关键节点选择，直至到达目标点G，跳出循环，输出最终路径。

图4 基于目标向量的关键节点选取策略

3.2 改进代价函数

传统A*算法的代价函数仅考虑当前节点与起始点和目标点之间的距离关系。其中：当前节点与起始节点之间真实距离代价g(N)可使已搜索路径最优，但无法抑制无效节点扩展；当前节点与目标节点之间的预估代价h(N)可以有效改善算法节点扩展盲目性，但目标趋向也将导致A*算法规划路径过早转折或紧贴障碍物边界，不利于行车安全。因此，本文结合地图预览模块获得的关键节点信息和道路边界信息，对A*算法进行改进。

3.2.1 距离表达函数

为了适应结构化道路特性和无人驾驶汽车运动学特性，本文选用Manhattan 函数计算当前节点至目标节点的距离[18]。Manhattan 距离是为规划方型建筑区块的最短行车路径而提出的，因此采用Manhattan 函数预估结构化道路中两点之间距离更接近真实值[19]。以图1为例，节点S与目标点G的距离为：

式中，dM为当前节点与目标节点之间的Manhattan距离；(Sx,Sy)、(Gx,Gy)分别为节点S和目标节点G的坐标。

3.2.2 障碍物判定规则

无人车在目标向量引导下选取下一关键节点，如图5所示，车辆在规划过程中基于障碍物判定开启增量式扩展搜索。当前车辆下一拟选定节点为节点N，此时车辆搜索域为图5 所示的长度为|Nx-Sx|、宽度为5 m（道路宽度）的矩形区域。其中，Nx为车辆拟选定节点的横坐标。判断此区域是否存在障碍物占据栅格节点，如果存在，启用增量式扩展进行无碰撞路径规划，反之，直接将车辆移动至拟选定节点N。

图5 障碍物检测区域示意

3.2.3 基于安全距离的碰撞场模型

实际行驶中，车辆应保持足够的安全距离。根据本车和前车的运行状态及相关因素估算实施制动干预距离，保证车辆不发生追尾碰撞[20]。典型的安全距离包括固定安全距离、基于自由滑行时间的安全距离、基于驾驶员预估模型的安全距离和基于车间距的安全距离等[21]。本文基于安全距离提出一种新的碰撞场模型，并将其应用于代价函数改进。

本文依据不同物体特点将障碍物主要分为道路边界、移动概率高但形状尺寸较小的障碍物和移动概率低但形状尺寸较大的障碍物。其中，道路边界选用固定距离碰撞场模型。针对另外两种类型的障碍物，经过对驾驶员驾乘习惯的分析，基于车间距模型设计，得到一种基于安全距离的碰撞场模型。

基于安全距离的碰撞场模型由车辆当前行驶速度、路面附着系数等参数共同决定：

式中，ds为不同类型障碍物的安全距离；k为不同类型障碍物的权重；v为车辆当前行驶速度；μ为车辆当前所在路面的附着系数；g=9.8 m/s2为重力加速度；du为单位距离，此处取值为1 m。

其中，不同障碍物类型定义如下：

a.沿道路宽度方向投影长度l∈[1,2)m 的物体，即为形状尺寸较大的障碍物，如道路侧方的静止车辆等，其移动概率较低，不易突然运动；

b.l∈(0,1)m的物体，即为形状尺寸较小的障碍物，如道路边沿的静止行人等，其移动概率较高，易突然运动。

经过仿真及对实际驾驶情况的分析，上述不同类型障碍物安全距离计算权重中，形状尺寸较大的障碍物取值为1.5，形状尺寸较小的障碍物取值为1.2。如图6 和图7 所示分别为不同形状尺寸的障碍物所对应的碰撞场模型。随着道路附着系数的降低和车速的增大，碰撞场距离增长速度呈现由缓及增的趋势，这与人类驾驶员驾乘习惯相符。

图6 形状尺寸较大的障碍物碰撞场模型

一般路面的附着系数不小于0.7。由图6、图7 可知，当路面附着系数达到0.7及以上时，考虑车速最高为20 m/s的情况，形状尺寸较大的障碍物碰撞场距离最大为44.16 m，形状尺寸较小的障碍物碰撞场距离最大为35.59 m，符合实际驾驶工况需求。

图7 形状尺寸较小的障碍物碰撞场模型

由ds可求得扩展栅格的总层数c为：

将碰撞场距离重新赋值为10 m×c，并作为扩展栅格最内层栅格代价值，依次向外以10 m的倍数进行递减赋值，如果障碍物扩展栅格中包含障碍物栅格，则不对其进行赋值。如图8所示，当车速为10 m/s，路面附着系数为0.8时，由式（2）可得ds=8.7 m，由式（3）可得c=1，因此直接将代价值10 m赋予障碍物边界外第1层栅格，其代价值等同于算法循环中车辆移动1个栅格距离的代价值。

图8 基于碰撞场距离扩展栅格

3.2.4 总体代价函数

改进A*算法代价函数为：

式中，o(N)为不同障碍物的碰撞场距离代价；k1、k2为不同代价函数的权重。

其中k1越大，路径趋向目标点速率越快，计算耗时越短，但这将会影响路径最优性，而k2取值则会直接影响规划路径与障碍物边界的距离，进而影响车辆行驶安全性。经过多次仿真和验证，本文取k1=2、k2=2。

3.3 路径平滑方式

准均匀B样条曲线不仅能够保证路径曲率连续，还能够满足路径的首尾约束，保证拟合路径部分与原路径平滑匹配[22]。

设准均匀B样条曲线为：

式中，{P1,P2,…,Pi,…,Pn-1,Pn}(Pi=(xi,yi),i=0,1,2,…,n)为曲线控制点坐标序列；{Ni,p(u)}(i=0,1,2,…,n)为非周期且非均匀节点矢量u=(0,0,0,0,up+1,up+2,…,un+1,un+2,un+2,un+2,un+2)上的p次B样条基函数[23]。

将各区间中整体参数u所表示的基函数替换为局部参数t∈[0,1]，准均匀三次B 样条曲线中第i段曲线的矩阵表达式为：

式中，di、di+1、di+2、di+3为特征多边形的顶点坐标；Mi为p次准均匀B样条的系数矩阵：

其中，mi,j计算公式为：

本文基于地图预览模块获取的道路转向关键节点和在行驶过程中产生的避障转向节点进行路径平滑，采用准均匀三次B 样条曲线对相应的轨迹进行优化。如图9 所示为基于道路转向关键节点和避障转向节点进行的路径平滑过程示意。其中，基于道路转向关键节点进行路径平滑时，共选用7 个控制节点，其位置分别为基于选定的关键转向节点向两侧各扩展横向相等间距为1 m的3个节点；基于避障转向节点进行平滑时，以2个变向节点为控制点，向前、后两侧扩展横向相等间距为1 m的3个节点。

图9 路径平滑方式

乘用车最小转弯半径通常为4～6 m，一般城市主干道交叉口转弯半径大于20 m，此处平滑后所生成的路径既满足汽车最小转弯半径约束，也满足道路交叉口转弯半径约束。

4 仿真验证

为了验证改进A*算法的性能，本文分别将传统A*算法、Weighted-A*算法和改进A*算法应用于基于校园地图所绘制的区域栅格地图上。

为验证改进算法的泛化能力和改进性能，本文采用小区域低复杂度场景地图和大区域高复杂度场景地图进行仿真对比验证。

本文设定相同的起始点和目标点，运行后分别记录不同算法路径长度la、平均计算耗时ta、扩展节点数量na、转向次数sa、与道路边界或其他障碍物边界的最小距离da（假设车辆宽度为1.6 m）等参数。其中Weighted-A*算法启发函数权重设为2，经仿真验证可知，此时路径效果和搜索速度较为均衡。

仿真环境计算机配置为：Windows 10 操作系统，Intel Core i5处理器，主频为3.0 GHz，运行内存为8 GB。

4.1 小区域低复杂度场景

小区域低复杂度场景指不存在其他类型障碍物，且道路结构较简单的场景。此类环境下，影响行车安全性和可行性的主要因素为车辆与道路边界的距离及转向次数。如图10 所示，小区域低复杂度场景栅格地图尺寸为30 m×30 m，对3 种算法设定相同起始点和目标点。A*算法属于最优搜索算法，因此其输出路径是唯一的，但受系统测试环境及硬件性能的综合影响，计算耗时在单次迭代中存在差异，经过多次迭代寻路的误差累积后，最终导致不同测试过程中计算耗时出现差异。为消除计算耗时的随机影响，在相同测试条件下对不同算法测试50 次，并计算各算法平均计算耗时ta，以充分验证改进算法计算效率。某次规划最终结果如图10所示。

图10 小区域低复杂度场景下不同算法行驶覆盖轨迹

由图10 可知，传统A*算法和Weighted-A*算法得到的路径结果一致，但其行驶覆盖轨迹，即车辆行驶过程中Z向投影面积移动覆盖区域，紧贴道路边沿，且转折较多，并不适用于该场景无人车行驶。由本文改进算法得到的路径不仅能够远离障碍物，同时能够尽量保持直行，保证了规划路径的安全性和可行性。

50 次测试计算耗时结果如图11 所示。由图11可知，改进A*算法在小区域低复杂度场景下计算耗时相比传统A*算法明显缩短，但其与Weighted-A*算法计算耗时接近。不同算法的计算耗时波动范围均保持在20 ms 范围内，可见改进算法的计算性能较为稳定。

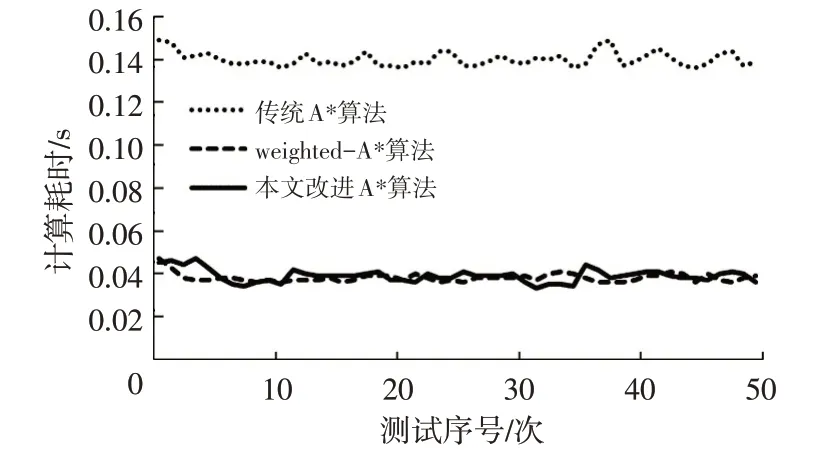
图11 小区域低复杂度场景下不同算法计算耗时

分别记录不同算法在50 次测试中的主要参数如表1 所示。其中改进率表示本文改进算法与其他算法不同参数值之差的绝对值占其他算法该参数取值的比例。

表1 小区域低复杂度场景下不同算法测试结果

由表1 可知，在小区域低复杂度场景下，本文算法扩展节点数量相对传统A*算法和Weighted-A*算法大幅减少，但本文算法引入循环判断，因此计算耗时相比Weighted-A*算法提升效果并不明显，仅提升8.3%。本文改进A*算法相对传统A*算法和Weighted-A*算法转折次数更少，路径与不同类型障碍物边界的最小距离也足以保障行车安全性。综上所述，本文改进算法的效果更加突出。

如图12所示为本文算法经过路径平滑处理后得到的优化路径，以微分的方法计算规划路径的曲率，得到此环境下路径最小曲率半径为6.5 m，满足车辆最小转弯半径约束，同时全路径曲率保持连续。为进一步判断平滑后路径的性能，对平滑路径与未平滑路径之间的偏离量及平滑路径与道路边界的距离最小值分别进行计算。由路径平滑方式可知，平滑路径在曲率最大处与未平滑路径偏离量最大，最大值为1.41 m，此时，其与道路边界最小距离为1.32 m。综上可知，平滑后的路径不仅满足车辆的运动学约束，同时仍能够与道路边界保持足够的安全距离，可见其相比未平滑路径更适合车辆的稳定控制[24]。

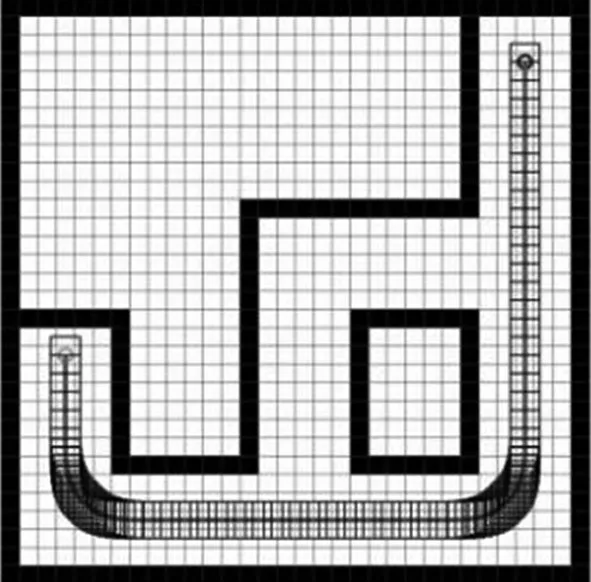
图12 本文改进A*算法平滑路径

4.2 大区域高复杂度场景

为进一步验证本文算法在大区域高复杂度场景下的性能，选择存在道路死角节点和不同类型障碍物的大尺寸栅格地图进行仿真。此类环境中影响行车安全性和可行性的主要因素为车辆与道路边界及不同类型障碍物边界的距离及转向次数。大区域高复杂度场景栅格地图尺寸为450 m×200 m，各算法某次规划结果如图13所示。

由图13 可知，传统A*算法和Weighted-A*算法在大区域高复杂度场景下，路径多转折、紧贴障碍物等问题更加突出，无法保证行车过程的安全性和可行性。但本文改进A*算法规划的路径不仅能够与道路边界保持一定距离，而且在应对不同类型障碍物时能够基于碰撞场模型进一步规划出更加安全可靠的避障路径，改进A*算法的综合优势更加明显。

50 次测试的计算耗时结果如图14 所示。改进A*算法在大区域高复杂度场景下计算耗时相比传统A*算法和Weighted-A*算法明显缩短。

图14 大区域高复杂度场景下不同算法计算耗时

不同算法测试参数如表2所示，由图2可知：在大区域高复杂度场景下，本文算法扩展节点数量相对传统A*算法和Weighted-A*算法大幅减少，计算耗时明显缩短；本文改进A*算法相对传统A*算法和Weighted-A*算法转折次数更少，路径与不同类型障碍物边界的最小距离也足以保障行车安全。

表2 大区域高复杂度场景下不同算法测试结果

如图15所示为本文算法经过路径平滑处理后得到的优化路径，以微分方法计算规划路径的曲率，得到此环境下路径最小曲率半径为6.2 m，满足车辆最小转弯半径约束，同时全路径曲率保持连续。对车辆平滑及未平滑路径之间的偏离度和平滑路径与道路边界的最小距离进行测量，测量结果同小区域场景，可见平滑路径有利于车辆的稳定控制。

图15 本文改进算法平滑路径

5 结束语

本文针对传统A*算法的缺陷进行了改进，通过地图模块的应用、基于安全距离的碰撞场模型的引入以及三次准均匀B样条曲线路径平滑方式，改善了算法的计算效率、可行性及安全性。

由于本文算法主要针对低速结构化道路场景进行路径规划，同时，搜索过程中仅考虑了单向行驶和静态障碍物，因此改进算法对高度复杂交互类交通区域仍无法适应。本文后续研究的重点是基于交通规则、驾驶行为的进一步探索和针对高速行驶等复杂动态工况的适应性研究[25-27]。