基于Massflow模拟的察隅县N047泥石流运动特征研究

赵思远 吴 琦 柴向阳

（1.华北水利水电大学地球科学与工程学院，河南 郑州 450003；2.河南省遥感地质勘察有限公司，河南 郑州 450000）

0 引言

通常认为降雨是诱发地质灾害的众多外部因素之一。雨水源源不断地汇入沟道，洪流裹挟着沟道内、岸坡上的松散固体物质沿沟道向下游方向流动，从而诱发泥石流灾害。因此本研究将对20 年一遇的暴雨条件下的N047 泥石流灾害采用Massflow 软件模拟，以确定其运动的基本规律，并模拟预测其在50 年、100 年一遇条件下的流量和泥深，为后期防灾、减灾提供必要的参考数据。

1 泥石流的基本特征

察隅县竹瓦根镇知美村N047泥石流地理坐标为98°08'12.10″E，28°28'18.13″N，流域面积为1.27 km2，流域内最高海拔4 481 m，最低点为3 490 m，相对高差达到989 m。如图1 所示，沟槽横断面呈“V”型，流域狭长呈带状，沟道较笔直，未见支沟，主沟纵坡比489‰。沟域纵向长度约2.1 km，呈对称分布，为季节性沟道，沟道内可见孤石。沟口处地形宽阔，相对弯曲。沟源周边群山围绕，呈“圈椅状”，植被覆盖率一般，沟道深切，侵蚀较严重。堆积区的扇形地完整性为95%，主轴坡降为248‰，扇面发展呈淤高趋势。扇长约155 m，扇宽约330 m，扩散角为95°，沟口至主河道（日东河）距离约580 m。该泥石流主要威胁对象为知美村居民点，威胁沟口两侧居民7户40人，房屋51间，威胁财产约619万元。

图1 泥石流全貌

2 泥石流的形成条件

该泥石流具备发生、发展所需的必要条件。①沟源处山体陡峭，呈立体的“圈椅状”结构，即三面环绕的凹槽地形。一面出口，后缘及两侧汇水面积较大，均利于汇水。形成区、流通区沟道陡峻、狭窄、深切，呈深“V”型，沟床纵坡较陡，水流在此可显著加速。②坡面出露主要为全新统残坡积物，较为松散破碎。沟道中游两侧斜坡侵蚀严重，在水动力作用下易破坏，形成堆积物，进一步堆积于坡体下部，成为泥石流的重要物质来源。③降雨充沛，且为该泥石流的唯一水源条件。

3 基于mssflow的泥石流运动特征

Massflow 软件是一款由中科院成都山地所欧阳朝军开发的具有二阶精度与自适应求解特点的地表过程动力学模拟软件［1］。是通过对三维Naiver-Stokes 方程［2］的深度积分得出质量与动量的控制方程，并利用有限差分法（MacCormack-TVD）结合MPICH 和OpenMP 技术［3-5］求解方程所开发的模拟软件。

3.1 模型建立

首先，采用卫星下载知美村N047 泥石流流域的等高线地形数据，利用ArcGis软件的空间分析功能转换成DEM 栅格数据。其次，使用ArcGIS 的“Arc Toolbox”工具箱中的“数据管理工具”，可以划分为5 m×5 m 大的计算网格，完成地形数据的处理。然后，根据ArcGIS 软件的“栅格转ASCII”转换工具，将已划分网格的DEM 数据转化成ASCII格式文档，可为Massflow 软件识别。最后，打开Massflow软件后台编译程序Microsoft Visual Studio，在程序代码中输入模型的相关信息，利用程序的“重新生产解决方案”“开始执行不调试”执行程序，再根据Tecplot软件，输出计算模型，如图2所示。

图2 泥石流三维模型

3.2 参数选取

3.2.1 重度。知美村N047 泥石流属沟谷型泥石流，结合野外调查成果，确定知美村泥石流重度γ为1.572 t/m3、泥沙修正系数φ为0.54，以及堵塞系数Dc为2.2。

3.2.2 流量。泥石流流量的计算设置在沟口及拟设工程治理部位的典型断面上，所有断面流量的计算皆在假设未实施工程治理的条件下进行。

首先，根据公式计算暴雨时的最大洪峰流量。该公式适合于全面产流条件下的全面汇流和部分汇流两种情况，可对横断面处的出水点在不同降水频率下的汇水流量进行计算，其计算公式为式（1）。

式中；QB为最大洪峰流量，m³/s；Ψ为洪峰径流系数；i为最大平均暴雨强度；F为集水面积，km2。计算结果见表1。

表1 暴雨洪峰流量计算结果

其次，采用雨洪法计算各断面的泥石流峰值流量。其计算公式为式（2）。

式中；Qc为泥石流峰值流量，m³/s；Fc泥沙修正系数；QP为频率为P的暴雨洪水流量；Dc为泥石流堵塞系数。计算结果见表2。

表2 泥石流峰值流量计算结果

3.2.3 流量过程线。依据流量过程线［6］（见图3）、野外勘察与泥石流多次反演，可知知美村N047泥石流为20年一遇流量所激发，历经30 min（1 800 s）。

图3 泥石流过程线

3.2.4 启动点与摩擦模型。启动点的选取需具备泥石流成灾的四个条件，即物源量丰富、降雨集中、沟道地形易于汇水，以及沟道地形能为泥石流启动提供势能空间。根据沟道内的监测结合启动点具备的条件，选取沟道中游处一点，如图2 泥石流三维模型中所标位置，作为模拟的启动点。Voellmy 模型改良自库伦模型并且适用于泥浆和泥石流灾害［7］，具有较好模拟效果，故本次模拟选取Voellmy模型。

3.3 模拟结果分析

通过对知美村N047 泥石流的反演，得出该泥石流在20 年一遇状况下60 s、100 s、600 s、900 s、1 500 s、1 800 s的泥深、流速，以及各时刻最高泥深与最大流速分布，如图4、图5、图6所示。

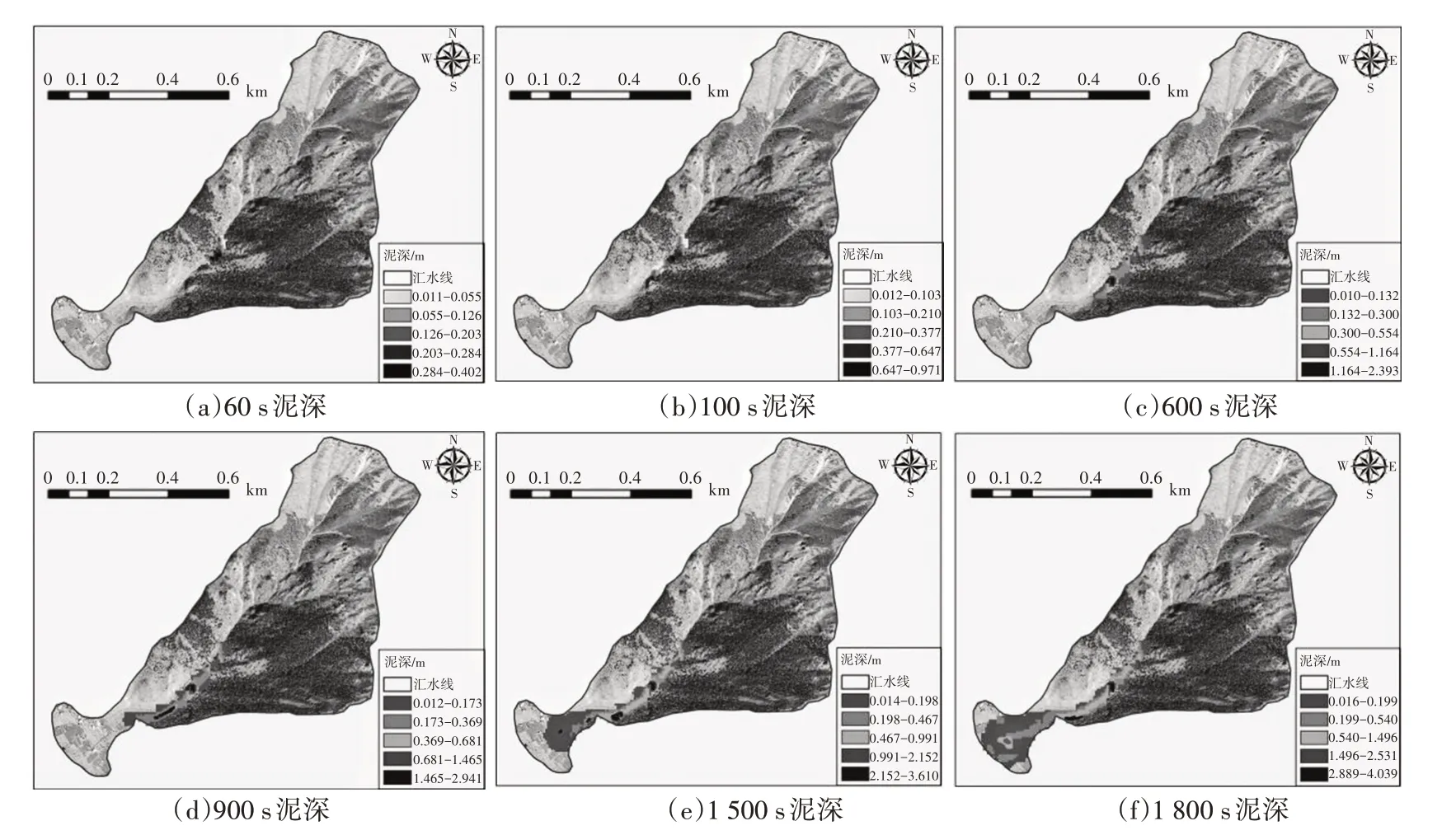
图4 不同时刻的泥深分布情况

图5 不同时刻的流速分布情况

各淤积点航拍照片如图7所示。分析模拟图可知。

图7 各淤积点照片

①0～60 s 时，泥石流刚启动，由于动能较低，流速缓慢，流体由于重力作用，沿着沟道向下运动，并不断侵蚀两侧沟岸的松散物，此时沟道内开始堆积，部分位于沟岸松散物下的沟道堆积较深，出现淤积（淤积点1）；60～100 s 时，由于后续流体的蠕动，加之沟道狭窄，流体增速明显，加速通过沟道中游，逐渐开始加速堆积；100～600 s 时，流体持续加速，后续流体冲破淤积点1，裹挟沟道内的松散物抵达淤积点2，该点位于沟道宽窄变化的交点且东侧岸坡侵蚀严重，松散物激增，形成淤积，堵塞沟道；600～900 s 时，泥石流持续加速至沟口转弯处，由于此处相对宽阔加之流体的弯道效应，开始出现淤积；900～1 500 s 时，流体流至堆积区，沟道显著变宽，沟口处流速达到最大值，并出现漫流，泥深增大，在转弯处形成淤积（淤积点3），堵塞沟道；1 500～1 800 s 时，流体逐渐减速，向沟口两侧漫流堆积，泥深不断增加，直到流体停歇。

②导致泥石流运动变化的主要因素为沟道地形的不断变换，沟道狭窄深切，地形陡峭，流速增大，沟道宽阔平缓，流速减小，泥位增加；沟道内出现淤积，是由于流体不断冲刷侵蚀沟岸，松散物大量涌入沟道造成沟道沟形发生变化，流体沿着沟道向下流动（即X、Y方向），因沟形空间的变化，流体在Z轴方向发生了漫流，即泥石流遇到障碍物时冲起爬高，此时动能部分转化为势能，部分能量有所消耗，导致流速降低，流体出现淤积。

③随着时间的增加，泥深在沟道内堆积深度越来越厚，直到泥石流停止运动，泥深不再增加。流速随着时间的变化，先增大后减小，最后泥石流停止运动，流速为0 m/s；流体经过了“蠕动-加速-减速-停歇”的过程。泥石流泥深随着时间的推移，在沟道内形成两处淤积点，泥深最高可达2.9～4.1 m，在沟道宽缓处和堆积区漫流堆积，泥深较为平均，深度为0.016～0.54 m，局部最深可达1.5 m。

3.4 模拟预测分析

根据不同降雨频率，预测知美村泥石流在50年一遇、100 年一遇的条件下，泥石流的泥深、流速如图8所示。

图8 50年、100年一遇泥深与流速分布

通过模拟20 年一遇、50 年一遇、100 年一遇的泥石流流态，得出1 800 s 时20 年一遇，泥石流最大流速5.134 m/s、最大泥深4.039 m；50 年一遇最大流速5.687 m/s、最大泥深4.950 m；100 年一遇最大流速6.476 m/s、最大泥深5.352 m；由此分析可得。

①在不同频率（P=5%、P=2%、P=1%）的降雨条件下，相同点泥石流的流速、泥深及流体在堆积区的范围均不相同，且这三者的大小均随流量的增加而增大。

②在不同频率（P=5%、P=2%、P=1%）的降雨条件下，沟道中的三个淤积点仍有不同程度的淤积，堵塞沟道，说明沟道两侧岸坡物源丰富。

3.5 模拟结果验证

方法一；现场测量泥石流冲出物2.1×103m3，通过ArcGis 对模拟20 年一遇泥石流堆积区的堆积面积及泥深测量，得出模拟的泥石流冲出方量为1.8×103m3，误差率-14%（即拟合度为86%）。

方法二；根据精度计算公式式（3），计算该模型模拟的精度［8］。

式中；Accuracy为精度；S0为实际泥石流堆积范围和模拟结果的重叠区域面积；Sa为实际堆积面积；Sn为模拟堆积面积。

如表3所示，知美村N047泥石流模拟的精度达84.5%，精度较高。

表3 知美村N047泥石流模拟结果验证

通过以上两种不同方式的验证，Massflow 模拟的知美村N047 泥石流，精度（拟合度）为84.5%，即模拟结果较为可靠。

4 结论

①本研究采用Massflow 数值仿真模拟软件对察隅县知美村N047 泥石流进行了不同降雨状况下的模拟（以20 年一遇状况为主），得出结果精度（拟合度）可达84.5%，即模拟结果较为可靠。

②该泥石流从开始到结束流体历经了“蠕动（0～60 s）-加速（60～1 500 s）-减速（1 500～1 800 s）-停歇（＞1 800 s）”的过程。而导致泥石流运动变化的原因是沟道地形的变化及堆积物涌入沟道而造成的沟形变化。

③该泥石流在不同频率的降雨条件下，相同点位流速与泥深并不相同，流体在堆积区的范围也不相同，它们均与流速呈正相关。