类比探究 提炼方法 彰显本质
刘园园

摘 要:专题教学在提高学生解题能力,发展学生数学思维等方面具有重要应用.在教学中,对于一些重点的、热点的、难点的问题可以以专题的方式呈现,让学生通过类比探究提炼解决问题的方法,感悟问题的本质,提高解题效率.
关键词:专题教学;方法;解题效率
近几年来,有关函数图象中角度存在性问题成了中考的宠儿.此类问题具有一定难度,考试均分不高.为了突破这一学习难点,笔者将以此类问题改编形成专题,采用从简单到困难的类比法,形成这一系列问题的解题思路,掌握解题的方法,提高解题效率[1].
1 问题呈现,体验解题策略
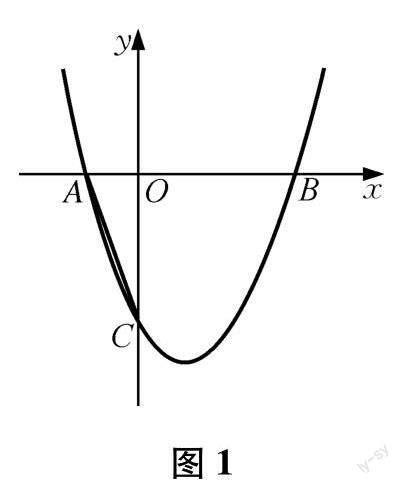
【例1】 如图1,抛物线y=x2-2x-3与x轴相交于A、B两点,和y轴交于C点,P是抛物线的动点,设m为点P的横坐标.
问题1:若点P使得∠PBA=45°,求m的值.
以上问题难度不大,学生很快就找到了解题方法.
生1:根据已知可求得点B和点C的坐标分别为(3,0)、(0,-3),连结BC,∠OBC=45°,又∠PBA=45°,所以点P就是点C,故求得m=0.结合图1可知,满足条件的点P不唯一.采用画图的方法即可以找到P点,该点是抛物线和直线的交点.同时,∠PBA=45°,这样可以得出PB所在的直线,解析式如下:y=-x+3.
接着与抛物线方程联立,并求解得x1=3(舍去),x2=-2,所以m=-2.
师:很好,生1是从代数的角度出发,根据交点坐标得到了m值.还有谁應用了这一方法呢?(学生纷纷举手)
根据课堂反馈,大多数学生都应用了这一方法.代数法思维起点低,符合大多数学生的思维习惯,故应用的人较多.
师:看来大家和生1一样厉害.请大家思考一下,该问题是否有更简捷的方法呢?
生2:先在图1上画出点P的大概位置,过点P作x轴的垂线,交于点D.因为∠PBA=45°,所以PD=BD,又点P的横坐标为m,用点P坐标表示线段,故有|m2-2m-3|=-m+3,也可以得到答案.
师:很好,生2从几何的角度出发,先是构造直观的几何图形,画出满足条件的角,然后将角度问题转化为线的问题,利用点的坐标解决了问题.
设计意图:开展教学过程中让学生学会站在不同角度去思考,采用不同的方法来解决问题,让数学思维被充分激活.这样可以为之后的解题提供更多的资源,促进学生解决问题能力的提升[2].
2 认知发展,提炼解题策略
问题2:已知条件不变,过点B作BD⊥AC于点D,是否存在第二象限内的点P,使得∠PBA=∠ABD?若存在,请求m的值.
在问题1顺利求解后,教师将问题进行拓展,给出了问题2.问题2与问题1相比,难度略有提升,为了让学生能够更好地解决问题,教师继续让学生进行小组探究,以此集思广益,让学生快速找到解决问题的突破口.
生3:按照生2的思路,可以先在第二象限内寻找点P,连结BP,然后想办法求出BP的解析式.如果想将BP的解析式求出来,先要将AC直线的解析式求出.再加上BD⊥AC的条件是可以求出BD解析式的,之后可以将D点的坐标算出.同时,令D′、D关于x轴对称.此时可以求得出BD′直线的解析式,而BD′的直线解析式与BP的相同.求出直线BP解析式后,与抛物线联立即可求得点P的坐标.这样虽然能够求解,但是感觉过程有些烦琐,所以没有直接计算,想看看是否还有其他解题路径.
师:说得很好,大家是否还有更为简捷的方法呢?
生4:我的思路和生3基本相同,不过在求直线BP的解析式时,我是先算直线BD与y轴的交点坐标,易得其交点坐标为(0,-3),这样根据∠PBA=∠ABD,可知直线BP经过(0,3),从而求得直线BP的解析式.
师:很好,充分利用图象特征,有效地简化了运算过程.你们还有其他想法吗?
师:很好,几位同学的思路都非常清晰,都是围绕“求直线BP的解析式”展开的,虽然运算过程有所不同,但是其解题思路基本一致.还有没有其他思路可以求解呢?是否可以运用几何法求解呢?(教师启发学生跳出原有思维的禁锢,尝试应用几何法求解)
生6:在图1上寻找点P的大概位置,过点P作x轴的垂线,且交于点E,则有∠ACO=∠ABD,又∠PBA=∠ABD,所以∠PBA=∠ACO,易证△ACO∽△PBE,这样BE=3PE,故3(m2-2m-3)=-m+3.
师:非常好,你是怎么想到这个方法的呢?
生6:我想到这个方法是受了问题1的启发,作垂线后发现相似三角形,于是就按照这个思路求得了m值.
师:很好,结合以上过程说一说,你有哪些发现?
生7:在求角度这个问题时只要利用好了图形,就可以直接把图转变成为线的问题,非常直观,再转化成为求交点坐标的问题就能轻松解决.
生8:采用代数法计算出交点的坐标,再将解析式求出,然后联立方程,运用方程的思想方法求得交点坐标.这种方法虽然运算过程烦琐,但是易于理解.
生9:在求交点坐标时也可以运用几何法,即根据图形特点构造特殊的图形,如特殊三角形或相似三角形,结合线段的等量关系,利用方程法解决问题.应用该方法可以有效规避烦琐的运算,有利于提高解题效率.
设计意图:在问题1的基础上进行拓展,让学生通过问题的解决总结归纳解决此类问题的方法,形成解题策略,提高学生解题效率.
3 借助应用,深化策略理解
通过以上两个问题的探究,解题策略已经形成,为了进一步加深策略理解,教师趁热打铁,给出了问题3.
问题3:若点P使得∠PAC=∠ACO,求m的值.
问题给出后,教师让学生独立思考,基于前面的解题经验,学生很快找到了解决问题的方法.
生10:取AP与y轴的交点为E.因为∠PAC=∠ACO,所以AE=EC.设OE的长度为x,则CE=3-x,AE=3-x,x只需要利用勾股定理就可以求出,之后E點坐标也可以得出,再得到这两值之后,就可以计算出AP直线的解析式,有效解决了问题.
生11:我前面的解题思路和生10相同,但是求出点E的坐标后,我没有求解析式,而是过点P作x轴的交点D,利用△AOE∽△ADP,求得了m值.
设计意图:教学中,为了检测学生解题策略的掌握情况,教师继续给出问题,加强解题策略,加深学生对这类问题的认知,提升运用水平.
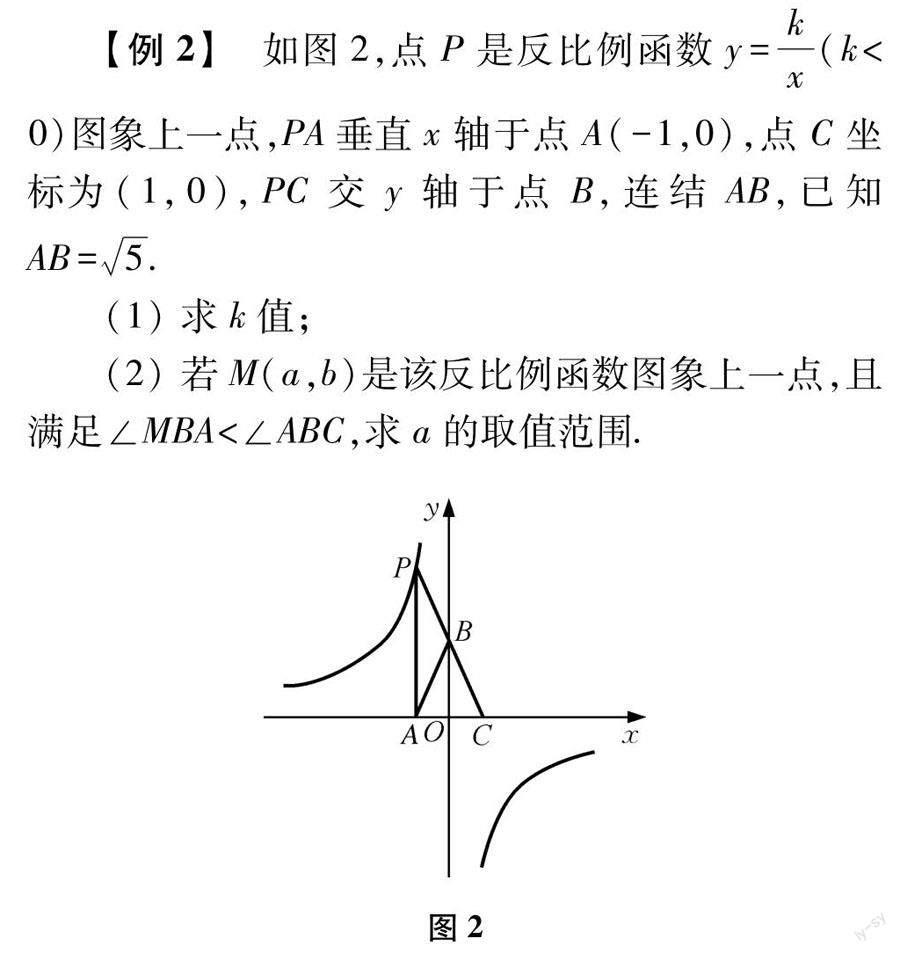
4 横向延伸,积累活动经验
问题给出后,教师先让学生独立思考,然后进行小组交流,并以互动的方式充分地展示学生的解题过程.在教师的启发和引导下,学生运用不同的方法解决了问题,积累了丰富的解题经验,升华了认知.
设计意图:将解决抛物线问题的经验迁移至双曲线问题上,通过对比分析巩固了原认知,让学生的思维得到了拓展,深化了解题的能力.很多数学的知识与方法是存在联系的,在教学中教师要多从“联系”的角度出发,引导学生将相似或相关的内容进行类比,继而明确问题的本质,提高学生解决问题的能力[3].
5 教学思考
专题型的解题教学,是十分重要的方法,需要采用专项练习,帮助学生掌握一类解题方式,从而实现会一题通一类的效果.
以习题为载体开展的专题训练,引导学生采用类比法,解决某些特定问题,以此提升解题效率.在专题训练中,教师要打破就题论题的格局,多给学生一些独立思考的时间和空间,引导学生通过对相似或相关内容的类比掌握解决此类问题的方法,并在解题的基础上让学生学会思考,学会学习.
若想提高专题训练的效果,教师应按照由浅入深的方式加以呈现,以此调动学生参与课堂的积极性.在解题教学的过程中,教师不要将方法和经验直接呈现给学生,需要让学生在解题时去感悟解决的过程、方法,以及解题时的灵感,促使学生有效发展思维能力.数学思想是数学学科的精髓,是数学学习的灵魂.正因为有了数学思想和数学方法的存在,数学知识变得更加系统、全面.本课中,先从形入手,确定解题思路,然后通过“数”与“形”的转化,高效地解决了问题.
总之,教师在设计专题时应以学生的思维为起点,通过“低起点、小坡度”的问题逐层深入,让学生在类比探究中积累解题经验,掌握解决一类问题的方法,提高教学效率.
参考文献:
[1] 黄悦军.核心素养视角下初中数学复习课教学模式的构建与实践[J].理科考试研究,2020(14):30-33.
[2] 高志军.例析初中复习课中小题大做专题的运用[J].中学数学,2021(4):41-42.
[3] 王荣华.核心素养视角下初中数学复习课教学策略[J].福建教育学院学报,2021(8):38-40.

