基于形式概念分析的交通监测传感网络贪婪性同步拓扑算法

叶青，史昕，孙梦薇，朱健

（1.国家山区公路工程技术研究中心，重庆 400067；2.重庆大学 大数据与软件学院，重庆 401331；3.长安大学 信息工程学院，西安 710064）

0 引言

面向交通监测的无线传感网络是智能交通领域新型应用场景中的关注焦点［1］，传感网络具备的部署便利性［2］、感知协作性［3］、交互泛在性等优点为传统交通监测应用带来显著的改变［4］。实现感知协作性依赖于传感节点之间的时间同步，即给特定区域内的传感节点提供一个公共通用的时间尺度［5］。该尺度旨在建立各个传感节点感知数据与共识时间之间的一致性映射关系，交通监测传感网络中与时序相关的所有操作均需解析该项映射关系［6］。时间同步算法主要由同步拓扑构建和时钟偏差估计构成，其中同步拓扑旨在明确同步数据报文的传输路径并决定报文数量的传输规模，也是执行时钟偏差估计的重要前提条件［7］。

交通监测传感网络的时间同步在能量有效性和场景适应性方面拥有独特的设计需求。能量有效性需求主要体现在：传感网络的时间同步主要依赖节点间同步报文的无线共享交换。文献［8］指出单个传感器节点将1 Kb 字节数据传输100 m 所需的能量等价于执行三百万条指令消耗的能量，传输大量同步报文将加快传感器节点能量的枯竭。然而在交通监测传感网络中，传感节点的核心任务是采集处理与传输共享交通流数据，如果传感节点能量不加节制地消耗在同步报文无线传输中，则传感节点的核心任务时间将大幅下降［9］。场景适应性需求主要体现在：交通监测传感网络的Sink 节点通常考虑供电和维护的便利性进行部署，同步拓扑算法的能量有效性不能受Sink 节点部署位置的影响；交通监测传感网络需要部署大规模的节点实现协同感知，同步拓扑算法的能量有效性不能受限于节点的部署规模；交通监测传感节点部署受限于道路边界呈现狭长部署形态［10］，部分节点的同步报文传输必须采用多跳中继方式实现［11］。

典型时间同步拓扑构建算法主要有以下几种：1）传感网路时间同步协议（Timing-synchronization Protocol of Sensor Network，TPSN）算法［12］利用层探测方法构建泛洪同步拓扑实现全网内时间同步，由于所有节点均参与同步报文传输，同步过程会产生大量冗余报文。2）PBS（Pairwise Broadcast Synchronization）算法［13］利用无线信道广播特性，同步位于相同广播区域内的节点，可有效减少同步报文开销，但局限于单跳同步。3）GPA（Group-wise Pair-selection Algorithm）［14］利用PBS 算法通过层与层之间的同步传递实现多跳同步，存在大量已同步节点重复参与同步报文传输的现象，从而引入较多额外的能量开销。4）DMSP（Distributed Multi-hop Synchronization Protocol）算法［15］是GPA 的一种改进，设置同步节点链表保存与筛选已同步节点，避免已同步节点重复参与同步，但是忽略了多基准节点的选择问题。5）FDMS（Fast Distributed Multiple-hop Synchronization）算法［16］根据节点邻接特征选择互为相邻的三个节点执行RBS（Reference Broadcast Synchronization）算法［17］，该算法对节点拓扑连通性要求较高，仅适用于具备强连通性的拓扑结构。6）EGTS（External Gradient Time Synchronization）算法［18］是FDMS 算法的一种改进，在邻居节点间选择参考节点多跳广播时间报文，能够减少多跳同步中已同步节点的重复报文传输量，但是同样继承了FDMS 算法对拓扑连通性要求较高的特点。7）LECFO（Linear Estimation of Clock Frequency Offset）算法［19］与ICPTR（Improved Clock Parameters Tracking and Ranging）算法［20］在时钟偏差估计方面分别改进了GPA 和TPSN 算法，但没有考虑同步拓扑对同步报文开销的影响。近年来，全局分布式同步拓扑（无汇聚节点）构建成为研究人员关注的焦点，它的鲁棒性较好，对传感器节点和关键通信链路状态不敏感，但是拓扑构建过程复杂度太高，节点集中式管理难以实现，且多跳性严重制约同步偏差估计的收敛速度［21］。

综上所述，交通监测传感网络由于Sink 节点的引入和节点的集中式管理需求，不适合采用分布式同步拓扑。在能量有效性方面，TPSN、EGTS 和ICPTR 算法在同步报文传输时存在大量冗余报文，难以满足交通监测传感网络对同步拓扑能量有效性的需求；PBS、LECFO 和DMSP 算法利用无线信道广播特性［22］，在减少冗余报文方面优于TPSN、EGTS 和ICPTR 算法，但对引入贪婪策略产生的局部最优问题没有给出相应的解决方法，同步拓扑能量有效性的提升能力有限。在场景适应性方面，TPSN、PBS 和ICPTR 算法没有考虑同步报文的多跳传输；LECFO、DMSP 和EGTS 算法实现了同步报文的多跳传输，但对多跳同步涉及的多基准节点选择问题没有给出明确的解决方法；同时，TPSN、LECFO、EGTS 和ICPTR算法的能量有效性受限于节点的部署规模，即增大节点部署规模后同步报文开销也呈现增大趋势。

针对交通监测传感网络时间同步拓扑的能量有效性和场景适应性问题，提出一种基于形式概念分析的交通监测传感网络贪婪性同步拓扑算法（Greedy Synchronization Topology algorithm based on Formal Concept Analysis for traffic surveillance based sensor network，GST-FCA）。该算法利用形式概念分析（Formal Concept Analysis，FCA）解析节点间的邻接特征关联性，实现多基准节点的筛选和广播元组（Broadcast Tuple，BT）的构建，以减少冗余性的同步报文开销；通过引入向上托管机制以缓解贪婪策略产生的局部最优问题，进一步降低已同步节点重复参与广播元组筛选的概率；最后设定不同仿真测试场景利用Matlab 验证GST-FCA 的能量有效性，GST-FCA 的能量有效性对节点部署位置、部署规模和道路部署具有较强的适应性，能够满足交通监测场景对节点进行大规模和便利性部署的应用需求。

1 问题描述

交通监测传感网络平面拓扑结构根据TPSN 算法的层探测广播机制可以转换为层次型拓扑结构，监测网络覆盖区域内各个节点被分配不同的层数标识Li，i（i＞0）表示被定义节点距离Sink 节点（首次广播层探测报文节点）的跳数。利用图论思想描述交通监测传感网络的时间同步拓扑结构，即无向图Gt(V，E)，其中：顶点V为交通监测传感网络中的传感节点集合；边E为传感节点间的邻接特征集合。定义Vi和Vi+1分别表示Li层和Li+1层节点所构成的集合，令V=Vi∪Vi+1。任意一 对节点vj和vk，且vj，vk∈V，如 果(vj，vk)∈E，则节点vj和vk存在邻接特征，处在对称性链接中的vj和vk互为邻接特征。

由TPSN 算法的层探测广播机制可得，处于Li+1层的所有节点在Li层必须至少拥有一个相邻层邻居节点，否则Li+1层的节点无法确定自身所处的层数。同步报文传输路径如图1 所示，如果Li层节点m与Li+1层节点n进行同步信息交换，即(m，n)∈E，利用同步信息交换的信道广播，Li+1层节点不仅可以通过与Li层节点的直接同步信息交换实现时间同步，也可通过侦听其余Li+1层邻居节点与Li层节点的同步信息交换完成时间同步。即节点n、m与n在Li+1层的共同邻居节点经过x轮的同步信息交换均可实现同步，同时节点m与节点n配对构成1 个广播元组。

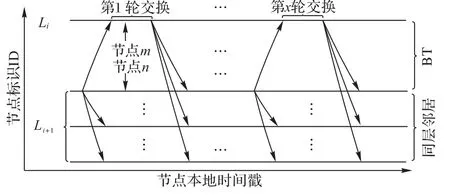
图1 同步报文传输路径示例Fig.1 Synchronization packet transmission path examples

广播元组能够引导局部邻域内节点的小范围同步，且可以避免所有节点都必须参与发送同步报文实现同步，从而减少同步报文的传输量，提升同步拓扑的能量有效性。因此，可以考虑在交通监测传感网络中构建广播元组以提升同步拓扑的能量有效性。根据节点邻接特征和广播元组的组成结构，GST-FCA 需要解决满足广播元组约束条件下的多基准节点同步问题。该问题的求解过程涉及两个关键点：如何解析同层与相邻层邻接特征的关联性构建广播元组和怎样减少因Li层节点同层邻接特征制约产生的局部最优解。

针对同层与相邻层邻接特征的关联性解析，由于交通监测传感节点受通信距离约束，单个广播元组难以实现Li+1层所有节点与Li层节点的时间同步，需要借助多基准节点同步（Synchronization with Multiple References，SMR）。从图论角度描述SMR 可表示为：

从Gt=(V，E) 中筛选出NBT个广播元组，其中：V=Vi∪Vi+1，Vi和Vi+1为Li层和Li+1层节点构成的集合；E为Li层和Li+1层节点的邻接特征集合；NBT表示实现Vi+1与Vi时间同步所需的最小广播元组数。如果Di表示NBT个广播元组在Li层的节点构成的集合，当Di中的元素唯一时，SMR 变为单基准 节点同 步（Synchronization with Single Reference，SSR）。

广播元组产生的局部最优解主要由Li层节点同层邻接特征制约已同步节点信息的共享范围引起。如图2 所示，vri表示位于Li层的基准节点，虚线表示节点的相邻层邻接特征，实线表示节点的同层邻接特征，Li+1层节点构成三个支配集。节点v3与vr3、v1与vr2、v6与vr5分别构成3 个广播元组（得到全局最优解），如果vr1与vr5不存在邻接特征，vr1会试图同步节点v6和v7；vr1与vr3不存在邻接特征，vr1会试图同步节点v3，此情形将额外增加2 个广播元组（得到局部最优解），原因在于vr1并不掌握v6和v7已被同步的信息，vr1不能确定v3已被同步。因此在多基准节点同步条件下，Li层节点的同层邻接特征会直接影响广播元组的筛选数目。

2 基于FCA的贪婪性同步拓扑构建

2.1 节点邻接特征关联性解析

FCA 是一种利用形式背景进行数据分析与规则提取的有力工具，提供了一种与传统数据分析和知识表示完全不同的方法［23］。它利用形式化的语境构造概念格（Concept Lattice，CL）表述组成本体的概念、属性及关联性。FCA 中概念的外延为对象集合，内涵为所有对象的共有属性集，外延作为CL 的行元素，内涵作为CL 的列元素，行元素与列元素的关联性用数值0 和1 表示，数值1 代表某对象与对应属性存在关联性，0 则代表不存在关联性。

本文引入形式概念分析，以不同层的节点集合与它的邻接特征为形式背景，以广播元组的组建结构为关联规则，对节点同层与相邻层的邻接特征进行关联性分析，从而构建广播元组和划分同步集合，具体过程如下。

定义1形式背景是由Q=(A，B，I)构成的三元组，I是A和B的二元关系（即I⊆A×B），以Li层节点集合X与Li+1层节点集合Y为例，每一个二元组(x，y)∈I表示节点x∈X与节点y∈Y存在邻接特征。

定义2假设形式背景Q=(X，Y，I)，φ表示幂集P(X)在幂集P(Y)中的映射关联性，ϕ表示幂集P(Y)在幂集P(X)中的映射关联性，映射关联性根据集合I判定，定义⊆X和⊆Y，(φ，ϕ)是关于P(X)和P(Y) 的伽罗 瓦连接（Galois Connection，GC）［24］，φ和ϕ定义如下。

定义4 关于二元组(x，y)的伪概念记为Rxy，Rxy为包含(x，y)的所有形式概念的组合：

分层条件下，节点间邻接特征关联性的分析步骤如下：

步骤1X赋值为Li层节点构成的集合，Y赋值为Li+1层节点构成的集合，P(X)定义为Li层节点构成的幂集，同理定义P(Y)；根据φ和ϕ的定义，若x为Li层任意一个节点，y为Li+1层任意一个节点，则φ(x)为与x存在邻接特征的Li+1层节点构成的集合，ϕ(y)为与y存在邻接特征的Li层节点构成的集合。

步骤2 根据式（1）求解关于二元组(x，y)的伪概念Rxy，从Rxy中提取包含(x，y)的所有形式概念，具体流程如下。

1）构建φ(x)的幂集P(φ(x))，从P(φ(x))中删除不含y的元素，构成集合P*(φ(x))，且P*(φ(x))⊂P(φ(x))。

2）若P*(φ(x))≠∅，定义集合P*(φ(x))的任意一个元素为Y*，计算ϕ(Y*)得到X*，X*表示与Y*所有元素存在邻接特征的Li层节点；计算φ(X*)得到Y*，Y*表示与X*所有元素存在邻接特征的Li+1层节点；于是，得到若干个包含(x，y)的形式概念，其中：r={1，2，…，T}，T为集合P*(φ(x))的基数。

其中：| · |表示集合的基数运算符。

步骤4 计算与节点x存在强关联性的Li+1层节点集合sync_node(x)：

同理，定义Y和Z均为Li+1层节点构成的集合，y和z分别为Li+1层的任意一个节点，同时定义所有形成的集合为，计算与节点y存在强关联性的节点集合sync_node(y)：

步骤5 根据图2 描述的广播元组结构示例，同步集合sync_set(x，y)由Li层节点x与Li+1层节点y的共同邻居节点构成：

步骤6 利用贪婪策略从所有同步集合sync_set(x，y)中找出集合元素数最多时所对应的(xk，yk)：

式（6）中的xk和yk将构成一个广播元组，删除与sync_set(xk，yk)中所有元素相关的邻接特征，可得到修改后的关于X和Y的二元关系I*，此操作目的在于删除已加入同步集合的节点，以避免这些节点重复参与同步集合的筛选。

步骤7 根据修改后的二元关系I*，从步骤1 开始重复执行，直至sync_set(x，y)为空，此时Li+1层节点均已加入已有的同步集合，Li层与Li+1层节点的同步拓扑构建完成。

2.2 局部最优问题优化及分层广播机制改进

2.1 节表明Li层节点的邻接特征（即连通性）直接影响已加入同步集合节点信息的共享范围，然而共享范围的局限性容易产生局部最优解。通过分析节点邻接特征关联性解析结果，可以得到：Li-1层节点（Li层的上一层相邻节点）能够获取较Li层节点更加充分的已同步节点信息。

证明 假设Li-1层节点构成集合为V，Li层节点构成集合为X，v为Li-1层任意一个节点，x为Li层任意一个节点，定义所有形成的集合为，利用式（7）计算通过Li-1层节点能够与节点x建立关联性的Li层节点构成的集合Ux：

由形式概念分析的计算过程可得，Ux中的元素即使与节点x不存在同层邻接特征，也能够通过Vk*中的元素（属于Li-1层集合V），与节点x共享已同步节点构成的集合，从而扩大节点x原有同步集合的共享范围。

因此，如果Li-1层节点能够拥有Li和Li+1两层邻居信息，可以缓解因Li层节点邻接特征制约引起的局部最优问题。考虑引入向上托管机制，将原来在Li层执行的广播元组构建算法上移至Li-1层托管执行。为了实现向上托管机制，提出针对TPSN 算法层探测广播机制的改进步骤如下。

改进步骤1 假设节点m所在层数为Li，当节点m接收到层数比i大的节点n发来的层探测数据包时，将节点n加入到节点m的相邻层邻接特征集合中，作为节点m的Li+1层邻居；当节点m接收到与i相等的节点n发来的层探测数据包时，将节点n加入到节点m的同层邻接特征集合中，作为节点m的Li层邻居。不同的是，TPSN 算法的层探测广播机制针对上述两类数据包执行丢弃操作。

改进步骤2 当交通监测传感网络的节点层数（假设最大层数为M）分配完毕后，从LM层到L1层执行回溯广播，与DMSP 算法不同的是，LM层节点分别广播它的同层邻居信息，Li(0 ＜i＜M)层节点分别广播它的同层和相邻层邻居信息，那么Li-1层节点至少可以拥有3 类信息：Li层邻居节点的同层邻居信息、Li层节点在Li+1层的邻居信息以及Li+1层邻居节点的同层邻居信息。

改进后的分层广播机制执行过程存在如下特点：

1）Li层节点执行回溯广播时，数据包只封装Li层和Li+1层邻居信息，并非Li层以下所有层的邻居信息。

2）假设网内节点总数为N，从空间复杂度分析，获得两层邻接特征所需广播报文的总体数量规模为O(N)，相较于获得单层邻接特征，不会呈现数量级上的显著增长［25］；

3）GST-FCA 与DMSP 算法均额外增加N个报文开销完成回溯广播，但是GST-FCA 中具备同层邻接特征的节点，因此不需要报文开销即可共享各自同步集合筛选结果。

2.3 GST-FCA的主要实现流程

GST-FCA 的主要实现流程归纳如下：

1）建立邻居信息：利用改进的层探测广播机制收集同层和相邻层节点的邻居信息；

2）向上托管执行：引入向上托管机制，将广播元组构建算法上移至Li-1层托管执行；

3）求解伪概念：针对Li-1层每个节点所包含的Li和Li+1层节点信息，求解分别由Li层任意节点x和Li+1层任意节点y构成的二元组(x，y)的伪概念Rxy；

5）计算强关联集合：选中使增益值取最大时对应的节点x和y，根据式（3）、（4）分别计算出与节点x和y存在强关联性的Li+1层节点集合sync_node(x)和sync_node(y)；

6）计算同步集合：根据式（5）得到由Li层节点x与Li+1层节点y的共同邻居节点构成的同步集合sync_set(x，y)；

7）修改邻接特征：根据式（6）找出同步集合元素数最多所对应的(xk，yk)，删除与sync_set(xk，yk)中所有元素相关的邻接特征，得到修改后的关于X和Y的二元关系I*；

8）判断重复执行：根据修改后的二元关系I*，返回第3）步重复执行，直至sync_set(x，y)为空集则退出，此时Li+1层节点均已加入已有同步集合，完成Li层与Li+1层节点的同步拓扑构建。

9）实现多层循环：定义网络最大层数为M，根节点位于0层，则参数i的取值范围为[ 1，M-1 ]，将参数i按照该范围分别依次取值以实现全网范围内的同步拓扑构建。

3 仿真实验与结果分析

3.1 同步报文开销仿真条件设置

利用Matlab 计算和分析GST-FCA 的同步报文开销，关键仿真条件和参数定义如下：

1）在100 m×100 m 区域随机部署交通监测传感节点2次，每次部署节点100 个；

2）在100 m×100 m 区域随机部署交通监测传感节点15次，每次部署节点数目呈递增趋势以控制节点的平均度数变化；

3）以高速公路双向6 车道的交通监测场景为例，设定应急车道宽度为3 m、行车道宽度为4 m、隔离带宽度为1 m，在100 m×31 m 区域按指定位置部署交通监测传感节点126 个，节点部署于车道宽度方向中心位置，沿车道长度方向部署间距为7.5 m；

4）考虑到报文无线发送消耗的能量与发送报文数量强相关，以报文开销量表征同步能耗的规模［15］，仿真结果中的报文开销量指单次同步中若要实现相同报文传输范围必需的同步报文传输量，且1 个广播元组单次同步需要2 个同步报文开销；每个广播元组中层数较大的节点用“▲”表示。

3.2 同步报文开销仿真结果与对比分析

仿真场景1：100 m×100 m 区域内部署节点数目为100，设定节点间通信距离为25 m。

仿真场景1 主要用于分析GST-FCA 在100 m×100 m 区域内随机部署条件下的同步报文开销，同时验证Sink 节点部署位置对同步报文开销的影响。该场景中，除Sink 节点外其余节点的位置呈现随机性，在方形区域随机部署相较于狭长部署形态的测试条件更具备一般性，且节点部署密度和平均度数拥有更大灵活性，可以更好地检验GST-FCA 的能量有效性以及Sink 节点部署位置对其影响。如果通过随机部署Sink 节点验证它对算法同步能量有效性的影响，可能由于Sink 节点部署位置太多，难以有效呈现所有仿真情况。结合交通流监测传感网络应用场景，Sink 节点的部署通常考虑供电和维护的便利性，一般部署在道路边缘或者中央隔离带。因此，选择Sink 节点坐标（50，50）和（50，100）两种情形进行仿真验证。

表1 是2 种Sink 节点坐标下多种典型同步拓扑算法在不同层内完成1 次同步所需的同步报文开销，表中各项数据根据分层拓扑结构以及各个算法的同步报文传输路径计算，其中，最优结果加粗表示，次优结果用下划线表示。从表1 可以看出，无论Sink 节点位于区域中心还是边缘位置，相较于对比算法，GST-FCA 的同步报文开销最小。当Sink 节点位于（50，100）时，将GST-FCA 各层的同步报文开销总和与次优的DMSP 的差值除以DMSP 的同步报文开销总和，可以得到GST-FCA 的同步报文开销的最小降幅为11.54%。由此可得，GST-FCA 利用基于FCA 生成的广播元组构建时间同步拓扑，可以有效解决TPSN、EGTS 和LECFO 算法存在的大量冗余性同步报文开销问题；GST-FCA 相较于DMSP 算法的单次同步报文开销更少，说明GST-FCA 可以降低已同步节点重复参与广播元组筛选的概率。Sink 节点的部署位置虽然直接影响其余传感节点的分层结果，但是GST-FCA 的同步能量有效性没有因为Sink 节点的部署位置产生较大影响。

表1 Sink节点在不同位置时的单次同步报文开销Tab.1 Synchronization packet overhead in one synchronization round for Sink node located in different positions

仿真场景2：100 m×100 m 区域内部署不同数目节点15次，节点数目变化范围为100～200，节点间通信距离为20 m。

仿真场景2 主要用于分析GST-FCA 在100 m×100 m 区域内不同节点平均度数下的同步报文开销，即验证节点部署规模对同步报文开销的影响。图3 给出不同节点平均度数对应的同步报文开销，图中每条曲线的走向趋势是经过多项式插值拟合的结果，Sink 节点坐标为（50，50）。可以看出，TPSN、LECFO 和EGTS 算法的同步报文开销随着节点平均度数的增加而提高，DMSP 和GST-FCA 的同步报文开销则整体保持平稳趋势，同时GST-FCA 的同步报文开销少于DMSP 算法。通常在限定区域内部署的节点数目越大则平均度数越大，而图3 说明DMSP 和GST-FCA 的同步报文开销受节点规模影响不明显，且将GST-FCA 与DMSP 的所有节点平均度数上的同步报文开销相加，同样按照场景1 中的方式计算，GST-FCA 的同步报文开销相较于DMSP 降低了24.59%。由此可见，GST-FCA 不仅可以减少大量冗余性同步报文开销，而且通过引入向上托管机制间接扩大已同步节点信息的共享范围，可以有效地缓解DMSP 算法因贪婪策略产生的局部最优解问题（达到24.59%）；同时，GST-FCA 能在保证同步能量有效性的基础上实现较大规模的节点部署，适用于交通监测应用场景。

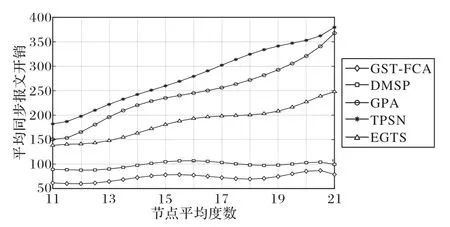
图3 不同节点平均度数对应的同步报文开销Fig.3 Synchronization packet overhead corresponding to different average degree of nodes

仿真场景3：100 m×31 m 的高速公路监测区域内，部署节点数目为100，节点间的通信距离为15m 。

仿真场景3 主要用于分析GST-FCA 在高速公路监测场景下的同步报文开销，即在道路和车道约束条件下验证GST-FCA 的能量有效性。图4 分别给出两种126 个节点在高速公路交通监测场景下的广播元组分布情形，节点间的通信距离越短则节点平均度数越小，定义沿道路行进方向为X轴，垂直道路行进方向为Y轴。图4 中节点平均度数为19.02，Sink 节点坐标分别为（50，31）、（50，15.5）。表2、3 分别列出Sink 节点位于边缘和中心时多种典型同步拓扑算法在不同层内完成1 次同步所需同步报文开销。同样按照场景1 中的计算方式计算同步报文开销降低的幅度。可以看出，无论Sink 节点位于边缘还是中心时，GST-FCA 的同步报文开销相较于TPSN、LECFO、EGTS 和DMSP 等算法都取得了最小，且开销至少降低39.16%、47.67%。Sink 节点位于道路边缘时，节点被划分为5 层，Sink 节点位于道路隔离带时，节点被划分为4 层，相同节点分布情况下，Sink 节点位于节点覆盖区域中心位置可以减少节点层数，有利于降低多跳同步的累计误差，同时GST-FCA 作用下的同步报文开销并没有较大差异性。由此表明，GST-FCA 通过FCA 产生的广播元组和向上托管机制构建时间同步拓扑，在受道路和车道约束的交通监测场景中，不仅可以实现较少的单次同步报文开销，而且DMSP 算法局部最优解问题的优化效果有进一步提升，尤其对于分层内节点数量越多且所处层越靠近Sink 节点的网络区域，它的优化效果更为突出，这些优势有利于GSTFCA 在交通监测场景中实现更好的时间同步拓扑能量有效性。

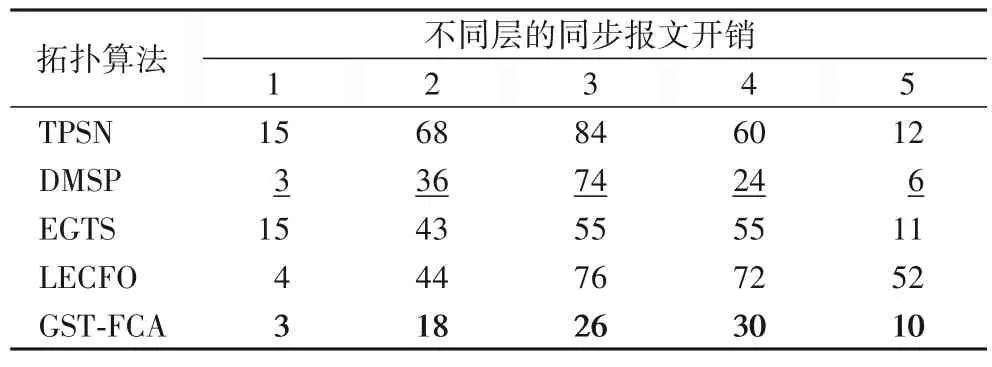
表2 Sink节点位于边缘时的同步报文开销Tab.2 Synchronization packet overhead when Sink node locating at edge

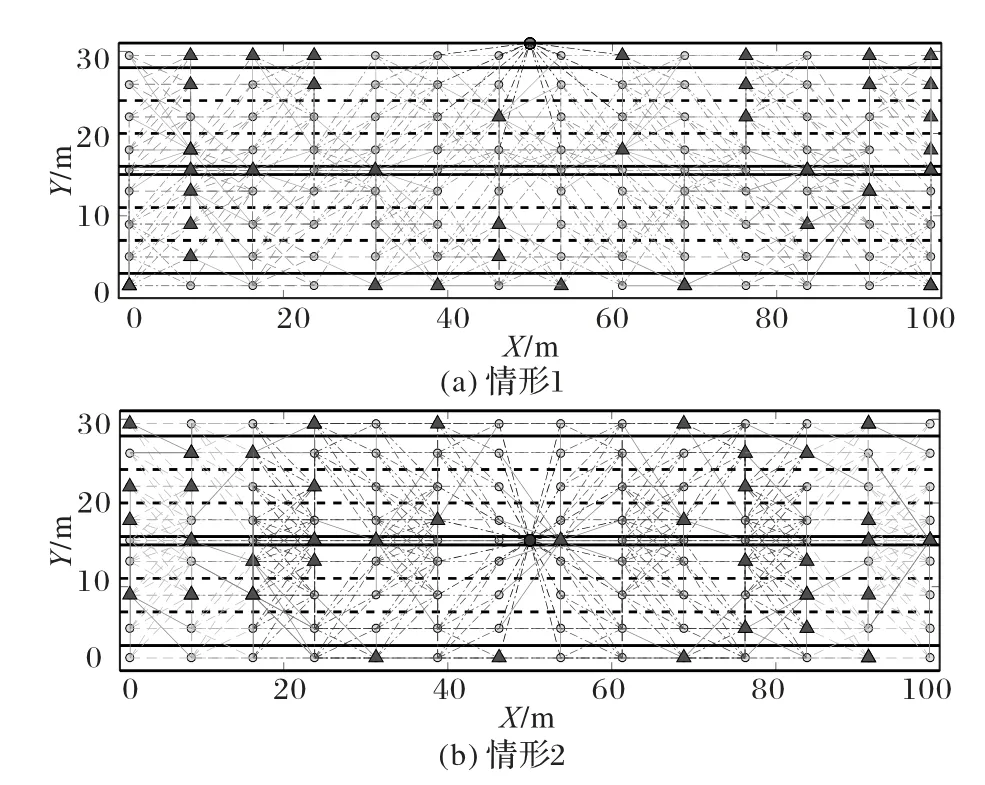
图4 126个节点的广播元组分布情形Fig.4 Scenarios of broadcast tuple distribution based on 126 nodes

无线传感器网络中报文无线传输存在丢包的可能性，且丢包率与报文大小、发送频率、传输距离、障碍阻拦、网络拓扑和冲突碰撞等因素有关联。如果考虑丢包因素，可引入平均丢包率作为丢包期望值，实际的同步报文开销估计通过必需的同步报文开销附加上丢失的同步报文数量进行计算。根据丢包率计算公式，如果同步拓扑算法单次同步必需的报文开销较大，其报文丢失数量相对较多，则实际同步报文开销也较大，扩展到多轮同步亦是如此。因此，仿真过程以必需的同步报文开销为参数指标在一定程度上可以表征同步拓扑算法的能量有效性。此外，如果进一步量化和分析不同网络参数约束下的实际同步报文开销，如丢包率、碰撞率、发送频率和传输距离等，可结合已构建的时间同步拓扑利用专门网络仿真平台进行测试与验证。

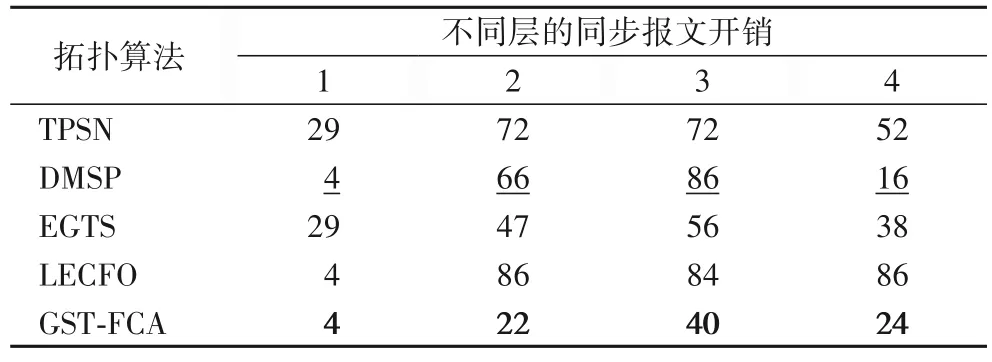
表3 Sink节点位于中心时单次同步所需同步报文开销Tab.3 Synchronization packet overhead when Sink node locating in center

4 结语

本文提出了一种基于形式概念分析的交通监测传感网络贪婪性同步拓扑算法GST-FCA，实现了多基准节点同步条件下的广播元组筛选，优化了贪婪策略所产生的局部最优解问题，并在Matlab 上验证了算法的能量有效性和场景适应性。测试结果表明，GST-FCA 能够进一步减少同步报文传输量，对Sink 节点的部署位置和网络节点的部署规模具备较强适应性，且能够在受道路和车道约束的高速公路交通监测场景下呈现出较好的能量有效性。在进一步的工作中，考虑到广播元组节点能量消耗相对较大，将研究基于Sink 节点部署位置的交通监测传感网络内节点同步能耗的均衡问题，以及结合丢包率、碰撞率等参数利用OMNet++或Network Simulator 平台对算法的报文开销作进一步量化分析。