基于时间注意力机制的时滞混沌系统参数辨识模型

尹聪，胡汉平

（华中科技大学 人工智能与自动化学院，武汉 430074）

0 引言

混沌系统具有动力学特性复杂、误差敏感、长期状态不可预测等特性，在保密通信等领域应用广泛［1］。而时滞混沌系统由于无穷维状态空间等特性［2］，因此具有更加复杂的动力学特性。时滞混沌系统的参数及时滞辨识对保密通信系统的同步控制［3］及安全性分析［4］具有关键意义，而混沌系统中时滞的引入带来的复杂的动力学特性在增强保密通信系统安全性的同时，也增大了系统参数辨识的难度。因此，对时滞混沌系统参数及时滞辨识问题的研究具有重要意义。

近年来，时滞混沌系统的参数辨识问题得到了广泛关注，其中基于同步控制的方法和基于智能搜索算法的方法是两种主流的辨识方法。基于同步控制的方法为混沌系统设计状态观测器，将系统参数视为状态观测器的状态变量，并根据稳定性理论使观测器的状态变量收敛于系统参数。此类研究主要关注同步控制在理论上的可行性［5］和针对具体系统的状态观测器实现［6-7］。基于同步控制的方法中状态观测器的设计依赖系统本身的特性，因此实现难度较大。智能搜索算法将参数辨识问题视为优化问题，以系统在参数和时滞的估计值下输出的状态序列与实际采集到的状态序列之间的误差为目标函数，通过全局搜索和局部搜索实现目标函数的最小化。智能搜索算法包括多项选择差分进化算法［8］、反馈教学优化算法［9］、人工雨滴算法（Artifitial Raindrop Algorithm，ARA）［10］、混合布谷鸟搜索算法（Hybrid Cuckoo Search，HCS）［11］、全局花 朵授粉算法（Global Flower Pollination Algorithm，GFPA）［12］、元胞鲸 鱼算法（Cellular Whale Algorithm，CWA）［13］等。它们的优势在于收敛性不依赖系统本身的特性，易于实现。但时滞混沌系统的系统参数和时滞与状态序列误差之间关系复杂，因此更容易陷入较差的局部最优，导致此类方法不能辨识出真实的系统参数。

随着深度学习的迅速发展，深度神经网络不仅在计算机视觉［14］、时间序列分析及预测［15］等领域取得了成功，而且在动力学系统的参数辨识领域也逐渐成为研究热点。文献［16-17］分别采用卷积神经网络（Convolutional Neural Network，CNN）和循环神经网络（Recurrent Neural Network，RNN）对Lorenz63 混沌系统和Tustin 二阶系统进行参数辨识。该类方法利用系统的多步状态序列或频域信息，通过学习系统状态序列与参数之间的函数关系实现对无时滞动力学系统的参数辨识，但并未考虑系统时滞对动力学特性的影响，不能用于时滞混沌系统在时滞未知时的参数及时滞辨识。因此，本文从代数方程求根的思想出发，提出基于时间注意力机制的参数辨识神经网络（Parameter Identification Neural Network with Temporal Attention，PINN-TA）模型。该模型首先通过时间注意力机制提取系统状态序列的关联特征，分析系统当前状态和时滞状态的关联性，从而实现对系统时滞的辨识及对系统时滞状态序列的逼近；再利用RNN 隐式逼近系统微分方程，构造系统当前状态、时滞状态与未知参数之间的代数方程；最终将代数方程的根作为系统参数的估计值，实现系统参数辨识。对时滞Logistic 方程、Ikeda 微分方程、Mackey-Glass 混沌系统等典型时滞混沌系统的仿真实验表明，相较于现有智能搜索算法，PINN-TA 模型得到的参数及时滞辨识结果在辨识精度和辨识速度方面均存在明显优势，能够满足时滞混沌系统参数辨识的精度和实时性要求。

1 系统方程

考虑由式（1）定义的时滞混沌系统：

其中：f为系统方程；τ为系统时滞；θ为系统参数。神经网络具有万能逼近性质，因此该系统可以由RNN 近似：

其中：δ为系统状态序列的采样间隔为RNN 对原系统方程的任意逼近。该网络定义了状态序列{xn}与系统参数θ之间的代数方程：

当时滞已知时，将系统当前的状态和时滞状态代入方程，此时系统未知参数θ即为式（3）所示的代数方程的根；而当时滞未知时，方程的构造则依赖时滞的辨识及系统时滞状态的近似。因此，式（1）的参数辨识问题可以分解为两个部分：时滞未知时对系统时滞τ的辨识，以及系统当前状态序列和时滞状态序列关于系统参数的代数方程的构造及求根。

2 参数及时滞辨识模型

本文模型通过时间注意力机制求得系统时滞状态x(t-τ)（即xn-m）的近似值，同时根据注意力权值求出系统时滞τ的估计值；并利用系统近似的时滞状态构建形如式（3）所示的代数方程，求得方程的根作为系统参数θ的辨识结果。因此，本文模型的输入为系统的状态序列，输出为参数和时滞的估计结果。模型的整体结构如图1 所示。

图1 参数辨识神经网络的总体结构Fig.1 General structure of parameter identification neural network

2.1 注意力网络结构

本文模型对时滞的辨识基于时间注意力机制实现。注意力机制能够提取输入时间序列中不同元素与目标输出之间的关联性，并将目标输出表达为输入序列的加权和［18］：

其中：J为输入序列的索引集；xj为输入序列的第j个元素；ci为目标输出序列的第i个元素；αij为注意力权值，该权值体现了ci与xj关联性的强度。在混沌系统的时滞辨识问题中，目标输出序列即为系统的时滞状态xn-m的估计值由于系统时滞辨识的依据是混沌系统状态的时间序列，且混沌系统为因果系统，因此本文模型中的注意力机制为时间注意力机制，且系统时滞不能为负，故式（4）可重写为：

其中：M为系统时滞m的搜索上界。式（5）将系统的时滞状态表达为从xn-M到xn的时间窗口内所有观测值的加权和。

在本文模型中，时间注意力机制的权值向量αn=［αn，0，αn，1，…，αn，M］基于RNN 提取序列的自相关特征输出。由于系统当前状态与时滞状态之间存在长距离相关性，且简单的RNN 由于存在梯度消失等问题，难以学习序列中的长距离关联特性，因此本文选择具备长程信息记忆能力的长短期记忆网络（Long Short-Term Memory，LSTM）［19］用于提取当前状态序列与时滞状态序列的长距离关联性特征。在系统辨识问题中，系统状态序列的时间双向关联［17］，因此将时间注意力机制中使用的LSTM 改为双向LSTM（Bidirectional LSTM，BiLSTM）。

如图1 所示，注意力网络中的BiLSTM 以状态序列｛xn｝与它的后向差分{xn-xn-1}为输入，通过BiLSTM 提取每一时刻状态的前向和后向关联性特征{dn}。{dn}反映了系统在当前时刻的状态如何受到过去时刻的影响，并如何影响系统未来的状态。将{dn}分别由两个前馈神经网络（Feed Forward Neural Network，FFNN），即FFNNq和FFNNk投影到查询向量空间{qn}和键值空间{kn}，并通过向量内积的方式和Softmax激活函数求得注意力权值向量αn。具体实现如下：

在注意力机制求解权值向量的过程中，LSTM 将序列的当前状态观测值及前后的各个观测值通过非线性变换投影到高维空间，并由状态序列在高维空间中的投影进行向量内积得出注意力权值。这一过程通过对来自给定系统的训练集的学习，定义了某种适用于给定混沌系统的、不局限于线性相关性的广义自相关函数：

输出的权值向量αn即自相关函数中每一时刻系统状态与自身平移个采样间隔后的状态在高维空间投影的内积的归一化。权值的相对大小体现了系统当前状态与各历史状态之间相关性的强弱，既表示了时滞取某一特定值的可能性大小，也给出了系统时滞状态的近似求法。该模型采用多层FFNN 将权值向量转换为系统时滞τ的辨识结果，并将系统历史状态的加权和作为系统时滞状态的近似，记作

时滞τ为采样间隔δ的整数倍（即m为整数）时，注意力权值向量应当为式（9）所示的独热（one-hot）编码：

2.2 求根网络结构

获得系统时滞状态的近似值后，由式（1）定义的原系统即可由RNN 逼近，形成关于系统状态序列、时滞状态序列和系统参数的代数方程，此时可求得代数方程的根作为系统参数的辨识结果。当待辨识参数＞1 时，若只有一组系统状态和时滞状态的观测样本，则代数方程一般有无穷多个根，因此仅凭一组观测样本无法求得唯一的参数辨识结果，此时需要联立多组观测样本代入代数方程后组成的方程组才能求得系统参数的唯一解。考虑到计算机有限字长的问题，由RNN 直接逼近系统方程，并将连续的若干组样本代入方程直接求根的方法可能会引入较大的舍入误差，影响参数辨识精度。形如式（3）的代数方程的构造和求根实质上定义了系统参数与状态序列之间的函数关系：

因此本文将代数方程的构造和求根问题转化为对函数G的逼近，并采用LSTM 实现这一函数逼近，从而求得系统参数的辨识结果。求根网络的具体结构如图2 所示。

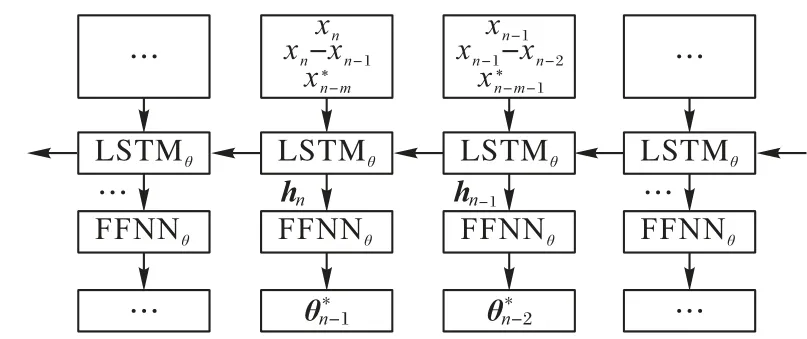
图2 求根网络的详细结构Fig.2 Detailed structure of root-finding network

求根网络中LSTM 的输入为系统状态序列{xn}与它的后向差分{xn-xn-1}，以及由注意力机制辨识得到的近似时滞状态LSTM 不仅隐式地实现了对原始系统方程的逼近，而且能够自适应地选取序列中的关键样本信息，并将现有状态序列信息下系统方程的最佳逼近和关键样本信息作为网络的隐含状态hn输出。hn由FFNNθ解码后即可得到系统参数的辨识结果。由求根网络隐式逼近系统方程并通过代数方程求根得到参数辨识结果的公式如下：

其中：由于注意力机制需要遍历系统状态序列的第（n-M）～n个样本才能求出系统在第n个样本对应的时刻下时滞状态的近似值，因此系统时滞状态的首个估计值需要在第M个样本处才能求出，即求根网络的输入是从系统状态序列的第M个样本开始的。求根网络在遍历状态序列的过程中更新系统方程的最佳逼近和关键样本信息，并由FFNN 解码得到系统参数的辨识结果。这一过程基于代数方程组构建和求解的思想实现，只需遍历状态序列一次，不需要对系统参数给出初始估计，避免了迭代式求解系统最优参数的过程，从而避免了智能搜索算法中的局部最优问题。

3 仿真实验与结果分析

3.1 实验设计

为验证PINN-TA 模型在时滞系统参数及时滞辨识中的有效性，以时滞Logistic 方程［20］、Ikeda 微分方程和Mackey-Glass 混沌系统［2］等3 种典型的时滞混沌系统作为待辨识系统对PINN-TA 模型进行仿真实验。它们的定义分别如式（12）～（14）所示：

在仿真实验中，每组实验的系统参数和时滞在表1 给出的取值范围中随机选取。

三个混沌系统的状态序列采样间隔δ分别取0.01、0.025 和0.5，每个参数-时滞组合仿真的时间长度为1 000δ。考虑到注意力机制存在如式（9）所示的性质，为避免端到端学习导致注意力网络陷入较差的局部最优，实验中为注意力网络单独生成训练集，并在训练求根网络前首先训练注意力网络。由于当且仅当时滞τ取采样间隔δ的整数倍时，时滞才能根据式（9）转换为独热编码，因此将注意力网络训练集的时滞τ取为采样间隔δ的整数倍，并随机选取参数θ，再仿真生成各参数-时滞组合对应的状态序列。除注意力网络训练集外，实验的求根网络训练集和测试集均通过表1 给出的取值范围均匀随机选取参数θ和时滞τ而成。考虑到呈收敛或发散形态的序列不是混沌序列，对保密通信等实际应用没有意义，实验剔除了各系统所有训练集和测试集中呈收敛或发散形态的状态序列，以及此类序列对应的参数-时滞组合，得到有效训练集和测试集的参数-时滞组合数量如表2所示。

表1 各参数和时滞的取值范围Tab.1 Value ranges of parameters and time delay

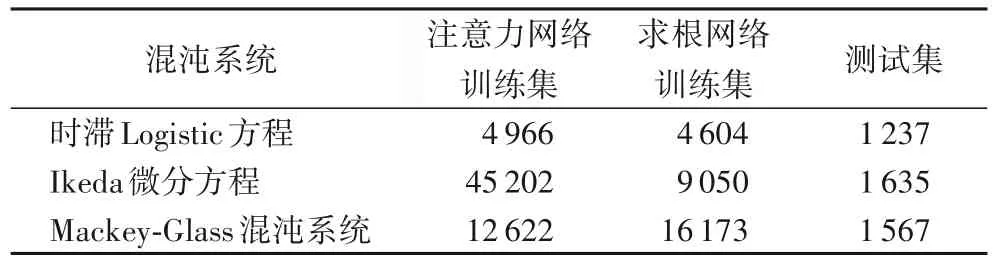
表2 各混沌系统的参数-时滞组合数Tab.2 Number of parameter-time delay groups of each chaotic system

为验证PINN-TA 模型在不同的时滞混沌系统中的通用性，所有混沌系统采用的神经网络参数及时滞辨识模型具有相同的结构，其中图1 所示的神经网络各个组成部分的神经元配置如表3 所示，dim（θ）表示待辨识参数的个数，括号中为神经元个数。

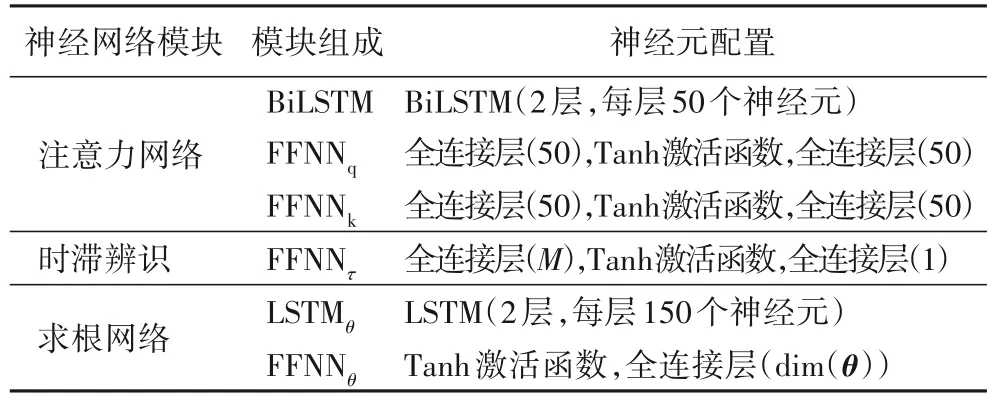
表3 神经元配置Tab.3 Settings of neurons

对各数据集的系统状态序列及参数和时滞进行归一化处理后，采用注意力网络训练集对注意力网络进行训练。训练过程中将时滞τ根据式（9）换算成的独热编码作为注意力网络的期望输出，采用注意力网络输出的权值向量与期望输出之间的交叉熵（Cross Entropy，CE）［21］作为损失函数，该损失函数可表达为正确时滞的注意力权值的负对数的均值：

采用0.001 的学习速率和Adam 优化器，batch 的大小为512（即每次取512 个参数-时滞组合评估一次损失函数）进行训练，对整个数据集迭代100 轮后网络基本收敛，损失函数的下降曲线如图3 所示。

图3 注意力网络训练过程中的损失函数值Fig.3 Loss function value of attention network during training process

注意力网络训练完毕后，采用求根网络训练集对求根网络和FFNNτ进行训练，并微调注意力网络的参数，以使注意力网络能够处理时滞不为采样间隔整数倍的情况。训练求根网络时，损失函数选取为求根网络和FFNNτ输出的参数和时滞的辨识值与真实值之间的均方误差（Mean Squared Error，MSE）：

优化器选取Adam，batch 的大小仍为512，求根网络和FFNNτ的学习速率为0.001，注意力网络的学习速率为10-5，对整个数据集迭代300 轮后网络基本收敛，获得对应混沌系统的参数和时滞辨识模型。

将系统状态序列按照第2 章中给出的格式输入PINN-TA神经网络模型后，神经网络在第M个采样间隔后的每个样本点都会输出一组时滞τ和参数θ的估计值，如图4 所示。本实验取神经网络对每组状态序列输出的参数θ的最后一个估计值和时滞τ的所有估计值的中位数，分别作为该序列的时滞τ和参数θ的辨识结果。

如图4 所示，参数θ的估计值在接收到系统状态序列的数个样本后迅速收敛至真实值，并维持在真实值附近波动。注意力权值分布图中，每个位置的颜色代表该时刻对应时滞的注意力权值，浅色表示高权值，深色表示低权值。图中正确时滞对应的位置可见一条水平亮线，说明注意力网络为正确时滞对应的采样时刻分配了高权值，有效地捕捉了时滞状态与系统当前状态的关联性。根据注意力权值求得的时滞τ的估计值在大多数时间内在时滞真实值附近波动，说明注意力权值向量可以作为辨识时滞的直接依据。

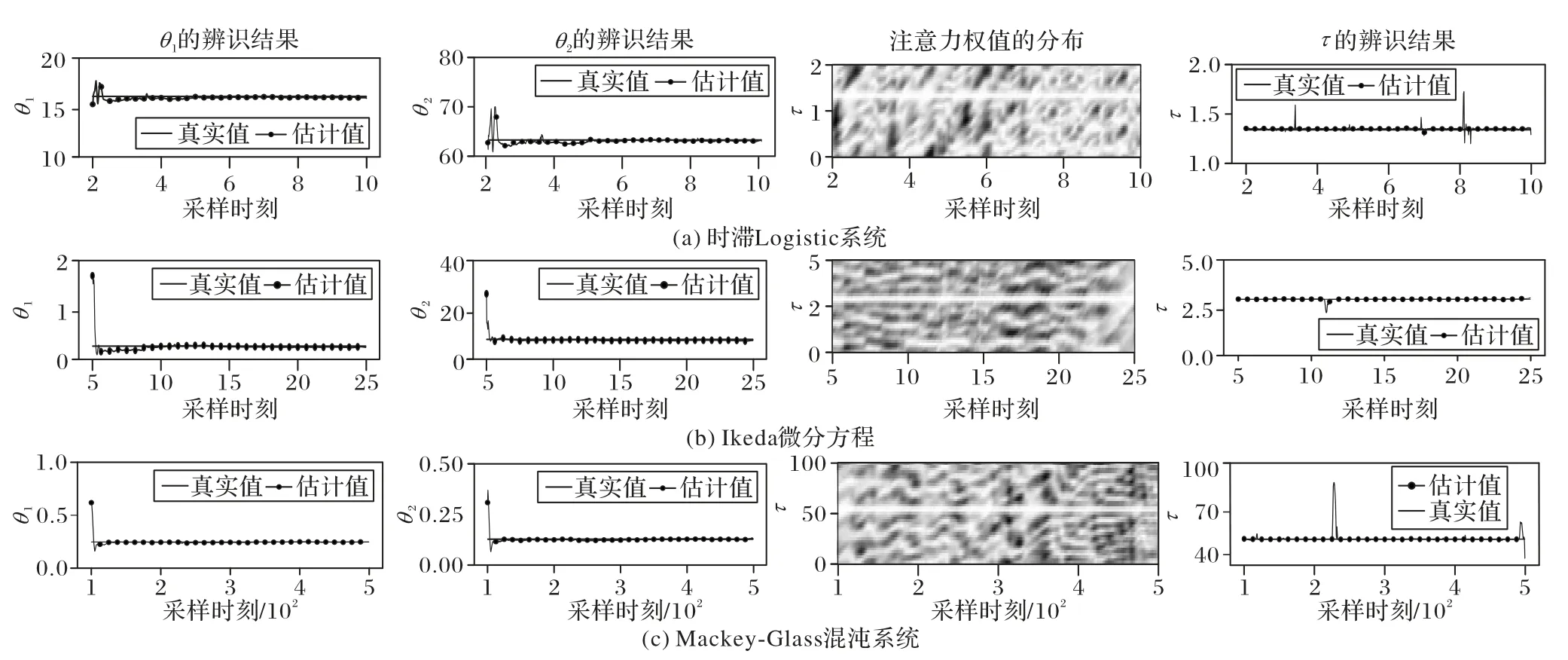
图4 各混沌系统的参数及时滞辨识结果Fig.4 Identification results of parameters and time-delay of each chaotic system

3.2 结果比较

为验证神经网络在时滞混沌系统参数和时滞辨识中的优势，本文将PINN-TA 模型的参数辨识结果与ARA、GFPA、HCS、CWA 等四种现有的参数辨识智能搜索算法进行比较，各智能搜索算法的搜索范围与表1 中定义的参数及时滞取值范围一致。所有智能搜索算法在100 次迭代后得到的最佳参数/时滞估计值作为智能搜索算法对系统状态序列的参数及时滞辨识结果。ARA、GFPA、HCS、CWA 均为近年来在混沌系统参数辨识中成功应用的智能搜索算法，分别以自然界中雨滴下落、花朵授粉、布谷鸟迁徙和鲸鱼捕猎过程为原型，设计全局搜索策略和局部搜索策略，以系统输出误差为需要最小化的目标函数，求得系统参数的辨识值。各智能搜索算法的参数配置如表4 所示，且目标函数均为系统在参数估计值下输出的状态序列与真实的状态序列{xn}之间的均方误差：

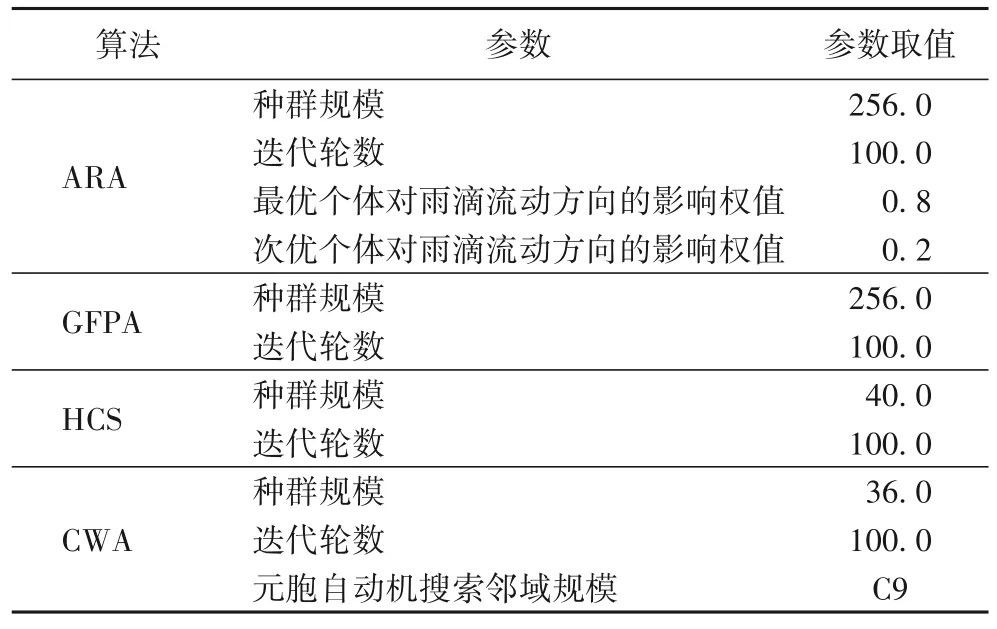
表4 各智能搜索算法的参数配置Tab.4 Parameter setting of each intelligent search algorithm

PINN-TA 模型与各智能搜索算法的参数及时滞辨识性能以参数和时滞的辨识结果与真实值之间的均方根误差（Root Mean Squared Error，RMSE）为评价标准：

表5 给出了PINN-TA 神经网络与各智能搜索算法的参数及时滞辨识结果。可以看出，PINN-TA 模型不仅具备良好的辨识精度，而且辨识速度优于现有的智能搜索算法。在时滞Logistic 方程的辨识实验中，相较于目前最优的ARA，PINN-TA 对两个参数的辨识均方根误差分别降低91.86%和93.54%，对时滞的辨识均方根误差降低98.27%。在Ikeda微分方程的辨识实验中，相较于ARA，PINN-TA 对两个参数的辨识均方根误差分别降低90.81%和98.64%，对时滞的辨识均方根误差降低94.29%。在Mackey-Glass 混沌系统的辨识实验中，相较于ARA，PINN-TA 对两个参数的辨识均方根误差分别降低99.13%和99.36%，对时滞的辨识均方根误差降低90.31%，且辨识耗时缩短至18.59～19.43 ms。现有的智能搜索算法将参数及时滞辨识问题描述为系统状态误差的最小化问题，侧重于根据系统参数与误差的关系，在参数的搜索空间中通过局部搜索及有限的全局搜索以求得使状态误差最小化的解。由于时滞混沌系统中参数和时滞与状态误差之间关系复杂，因此在搜索空间较大时容易陷入局部最优，导致各智能搜索算法的辨识误差普遍偏高。而PINNTA 模型从系统参数与状态序列的代数关系出发，基于代数方程求根的思想，在利用注意力机制挖掘状态序列关联性特征的前提下，利用LSTM 逼近系统参数与状态序列代数方程的根，避免了智能搜索算法陷入局部最优的问题，取得了良好的辨识精度。

表5 PINN-TA与各种智能搜索算法对典型时滞混沌系统的辨识结果Tab.5 Identification results of typical time-delay chaotic systems obtained from PINN-TA and different intelligent search algorithms

4 结语

针对时滞混沌系统的参数及时滞辨识问题，本文提出了基于时间注意力机制的参数辨识神经网络（PINN-TA）模型。通过基于BiLSTM 的注意力机制提取系统状态序列的时间关联特征，并利用LSTM 隐式地逼近系统方程，构造系统参数与状态序列的代数方程，从而通过对隐式构造的代数方程近似求根得到系统参数的辨识结果。对三种典型时滞混沌系统的大量参数辨识实验表明，相较于现有的智能搜索算法，PINN-TA 模型在辨识精度和辨识时间方面具有显著优势，能有效解决时滞混沌系统参数辨识问题，可应用于混沌同步控制、保密通信等工程应用。未来的研究将主要集中于以下两个方面：一是拓展模型的适用范围，使其能够实现对多维状态序列或多个时滞的混沌系统的参数辨识；二是改善模型的可解释性，求出隐含在求根LSTM 参数和隐含状态中的系统代数方程及关键样本。