基于多头软注意力图卷积网络的行人轨迹预测

彭涛，康亚龙，余锋，张自力，刘军平，胡新荣，何儒汉，李丽

（1.纺织服装智能化湖北省工程研究中心（武汉纺织大学），武汉 430200；2.湖北省服装信息化工程技术研究中心（武汉纺织大学），武汉 430200；3.武汉纺织大学 计算机与人工智能学院，武汉 430200）

0 引言

行人轨迹预测基于当前已知行人随时间变化的笛卡儿坐标集，预测未来时间内行人的运动轨迹。行人轨迹预测在监控系统、无人驾驶等应用领域有着重要作用［1］。在监控系统下，行人轨迹预测能够判断是否有异常情况；对于无人驾驶系统，行人轨迹预测能够提供关键的行人轨迹信息。

在早期的工作中，Helbing等［2］提出了社会力模型描述行人间的作用力；Keller等［3］组合贝叶斯滤波器和运动学模型以预测行人的轨迹；Kooij等［4］建立了基于上下文的动态贝叶斯网络以预测行人轨迹。上述方法需要对模型进行严谨的建模，存在一定局限性，而基于深度学习的轨迹预测方法则不需要预设固有的物理模型，凭借大规模数据集就能拟合较好的映射关系。目前，大量基于深度学习的轨迹预测方法被提出，社会长短期记忆（Social Long Short-Term Memory，S-LSTM）网络［5］是首个使用深度学习预测行人轨迹的算法。S-LSTM 使用循环神经网络（Recurrent Neural Network，RNN）对每个行人进行建模，并设立一个社交池计算行人之间的相互影响，通过发掘行人之间的隐藏信息预测行人的轨迹。社会生成对抗网络（Social-Generative Adversarial Network，S-GAN）［6］使用生成对抗网络（Generative Adversarial Network，GAN）预测多模态轨迹，并提出一种池化机制根据行人之间的相对距离计算行人之间的交互作用。社会时空图卷积神经网络（Social Spatio-Temporal Graph Convolutional Neural Network，Social-STGCNN）［7］直接将行人的轨迹建模为图，并对边进行加权，由行人之间的相对距离表示行人之间的交互作用。这些算法忽略了行人交互作用的有向性，而稀疏图卷积网络（Sparse Graph Convolution Network，SGCN）［8］提出了稀疏有向交互作用算法解决了行人之间交互作用无向的问题。但SGCN 忽略了两个问题：1）行人在同一空间位置下有意义的位置交互信息；2）同一时间单个行人与全局行人交互对行人轨迹预测的影响。为解决上述问题，本文提出多头软注意力（Multi-head Soft ATTention，MS ATT），即多头空间和通道注意力，如图1 所示，其中⊙为哈达玛积。空间注意力关注行人在同一空间位置下交互信息的位置信息；通道注意力则考虑什么样的交互信息才有意义。

图1 多头软注意力的结构Fig.1 Structure of multi-head soft attention

为解决同一时间下单个行人与其他行人交互对行人轨迹预测的影响，引入内卷网络Involution［9］。内卷网络的卷积核Involution Kernel 在每个空间位置下都不同，根据单个位置邻域的元素动态生成对应位置下的Involution Kernel 并与输入的特征图进行全局乘加运算，从而解决同一时间下单个行人与其他行人交互对行人轨迹预测的影响。在此基础上，提出一种稀疏内卷学习，如图2 所示，利用MS ATT 获取行人之间的交互得分，通过内卷网络获取单个行人与全局的互动信息，生成更高层次的交互特征。使用Zero-Softmax 函数的归一化操作修剪多余的交互作用后，可以获得稀疏空间和稀疏时间邻接矩阵。在得到稀疏邻接矩阵后，考虑到非对称归一化稀疏邻接矩阵可以表示稀疏有向图，通过联合学习稀疏空间和稀疏时间有向图，建模稀疏有向交互和轨迹的运动趋势，利用图卷积网络（Graph Convolutional Network，GCN）级联学习轨迹特征，并使用时间卷积网络（Temporal Convolutional Network，TCN）［10］估计双高斯分布参数，生成预测轨迹。

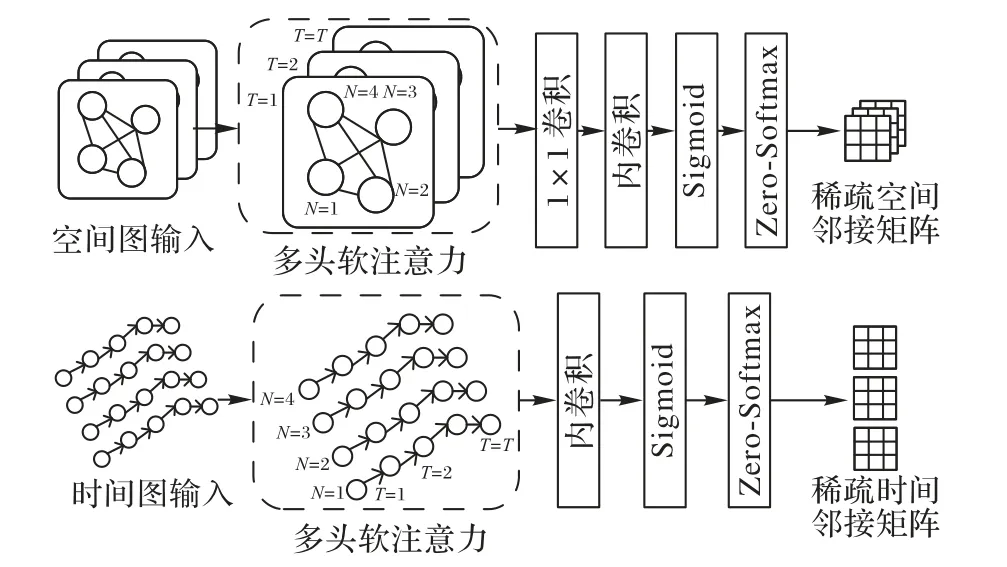
图2 稀疏内卷学习的结构Fig.2 Structure of sparse involution learning

1 相关工作

1.1 行人轨迹预测

对于行人轨迹预测，SoPhie［11］使用卷积神经网络（Convolution Neural Network，CNN）从整个场景中提取特征，对每个行人使用双向注意力机制，然后连接注意力输出与视觉CNN 输出，以此生成未来的轨迹。PITF（Peeking Into The Future）［12］则考虑了行人周围的环境因素，即人与场景的交互和人与对象的交互。S-BiGAT［13］使用LSTM 对每个行人的轨迹以及图注意力网络（Graph ATtention network，GAT）［14］的交互进行建模。RSBG（Recursive Social Behavior Graph）［15］注意到一些远处成对的行人之间存在很强的交互作用，因此邀请社会学家根据特定的物理规则和社会学行为将行人手动分为不同的组。STAR（Spatio-Temporal grAph tRansformer）［16］通过Transformer 框架对空间交互作用和时间依赖性进行建模。SGCN 则提出了一种稀疏图卷积网络，分别对空间图和时间图进行建模，从而学习行人之间的交互作用和行人的运动趋势以预测行人的轨迹。图卷积神经网络的轨迹预测模型TP-GCN（Trajectory Prediction GCN）［17］利用LSTM 提取行人轨迹的运动特征，将行人视作顶点，相互关系视作边，并根据视觉盲区范围筛选无关顶点间的连接权重，然后使用GCN提取不同轨迹之间的交互特征。张志远等［18］使用行人间的距离和方向信息构建注意力模型，使用GAN 生成轨迹。空时社交关系池化行人轨迹预测模型（Space-time sOcial relationship pooling pedestrian trajectory Prediction Model，SOPM）［19］使用空时社交汇集机制学习行人轨迹特征的全部社交，再利用关系池化方法，将空时社交特征池化为“引力-斥力”社交，再将这种社交作为RNN 解码器隐藏部分输入，以预测轨迹。SA-GAN（Social-Attention GAN）［20］定义了一种新型社会关系，使用注意力模型对社会关系建模，探索不同池化汇集机制对轨迹预测的影响。程媛等［21］利用非参数估计对起点与终点相同的轨迹构建密度分布的不确定轨迹模型，在预测阶段，通过KS（Kolmogorov-Smirnov）检验方法与具有相同起点的不确定轨迹模型进行匹配，其中匹配程度最高的不确定轨迹即为预测轨迹。上述方法都使用GAN 生成更真实的轨迹，本文算法则构建时空图，利用GCN 提取轨迹特征。本文算法与STGCNN、SGCN、TP-GCN 相似，将人视作顶点，交互作用视作边，然后使用GCN 提取交互特征。

1.2 图卷积和内卷网络

GCN［22］将非欧氏空间的图数据转换为欧氏空间图数据。目前的GCN 模分为两类：1）光谱域GCN。以光谱分析的形式考虑图形卷积的局部性，设计了基于图傅里叶变换的卷积运算，由于拉普拉斯矩阵的特征分解，要求邻接矩阵对称。2）空间域的GCN。卷积核直接应用于图节点及邻居节点，在边缘进行卷积，适用于非对称邻接矩阵。对于空间域的GCN，GAT 使用注意力机制对节点之间的交互进行建模；为了处理时空数据，时空图卷积网络（Spatial Temporal GCN，STGCN）［23］将空间GCN 扩展到时空GCN 进行基于骨架的动作识别，从局部时空范围聚集节点；SSTGCNN 利用STGCN 从图中提取空间和时间信息，预测行人的轨迹；SGCN 与已有的全局控制网络不同，通过学习的稀疏邻接矩阵聚合节点，动态确定要聚合的节点集，而本文算法的网络与SGCN 相似。

内卷网络Involution 在设计上与普通卷积（Convolution）的特性相反，在通道维度共享卷积核（Kernel），在空间维度采用空间位置下自动生成的Kernel 进行建模。在通道维度上，Convolution 的每个通道都有一个独立、私有的Kernel；而Involution 在通道维度上共享Kernel，将通道数分成G个组，每个组共享一个自己的Involution Kernel。在空间维度上，Convolution 共享一个Kernel，采用滑动窗口的方式进行卷积运算；而Involution 在空间上每个Pixel 的Involution Kernel 都不相同，每一个像素都会有一个Kernel。Involution Kernel 的大小为H×W×K×K×G，H、W分别表示特征图的高和宽；K为卷积核大小；G表示通道组数，G＜C，C为通道数，表示通道共享G个Kernel。Involution Kernel为H∈RH×W×K×K×G。Involution 的操作主要分为两个步骤：首先生成Involution Kernel，然后将Involution Kernel 和输入的特征图进行Multiply-add 运算生成对应位置的特征图。

1.3 注意力机制

通道注意力［24］利用通道间的特征关系产生通道注意力图，它侧重于捕获输入图像中有意义的特征。通道注意力包含平均池化和最大池化操作，其中：平均池化（AvgPool）可以聚合输入图像全局的特征信息；最大池化（MaxPool）则可以捕获输入图像最显著的特征信息。将产生的平均池化和最大池化特征输入共享多层感知机（MultiLayer Perceptron，MLP）网络，共享MLP 网络由MLP 和一个隐藏层组成。共享MLP 网络可以通过压缩隐藏层的通道维度减少网络参数开销，同时保证高效地计算通道注意力。最后，将共享网络的输出特征进行求和得到最终的通道注意力。

与通道注意力不同，空间注意力［24］利用空间的特征关系生成空间注意力图，侧重于信息在何处，是对通道注意力的补充。为了计算空间注意力，沿通道维度应用平均池化和最大池化操作，并连接它们以生成特征信息，最后应用卷积层生成空间注意力图。分析表明，沿通道维度应用池化操作可以有效地突显信息区域。

2 多头软注意力图卷积网络

现有工作能够轻松捕获行人之间的交互作用，但难以捕获行人在同一空间位置下有意义位置的交互信息。现存方法在建模同一时间下单个行人与全局行人的交互时既不直观，也难以解释特征状态下的物理意义。为解决这些问题，本文提出一种多头软注意力图卷积网络，如图3 所示，⊗表示在C个通道上进行乘法运算，⊕表示在K×K空间邻域内聚合求和运算。首先使用稀疏内卷学习从空间图和时间图学习稀疏有向交互和运动趋势；然后，通过GCN 从稀疏空间和稀疏时间有向图中提取交互作用和运动趋势；最后，将学习到的轨迹特征送入时间卷积网络预测双高斯分布参数，该参数即预测的行人轨迹。

图3 多头软注意力图卷积网络的结构Fig.3 Structure of multi-head soft attention graph convolution network

2.1 稀疏内卷网络

2.1.1 图输入

2.1.2 多头软注意力

在拥挤环境下，行人自然行走时为避免相互之间发生碰撞，行人之间会产生一种交互作用力。为了建模这种交互作用，使用MS ATT 计算行人之间交互作用的得分矩阵。引入多头形成多个子空间，让网络能够关注不同方面的信息。在空间图下，时间独立，多头表示不同时刻的交互信息，即每个头关注不同时刻的交互信息；在时间图下，每个人的运动趋势特征独立，多头则表示不同行人的运动趋势特征，即每个头关注不同行人的运动趋势特征。所谓MS ATT 就是多头通道注意力和空间注意力的融合。通常利用通道注意力获取行人之间有意义的交互Mc(Espa)，如式（2）所示；利用空间注意力获取空间位置下行人之间交互的位置信息Ms(Espa)，如式（3）所示。MS ATT 将通道注意力点乘空间注意力，经过一层平均池化操作和一个卷积操作，最后经过一个Sigmoid 激活函数操作，得到多头软注意力Rspa，如式（4）所示。

其中：φ1(·)为全连接层表示的线性变换；σ1为Sigmoid 激活函数；Espa表示空间图嵌入表示线性变换的权值；Rspa为行人之间交互作用的得分矩阵。

2.1.3 稀疏空间有向图

为了得到行人之间更详细的交互信息，首先将Rspa沿时间通道进行1× 1 融合，得到空间-时间交互特征；然后通过内卷，产生更高层次的运动交互Ispa。在时间通道上，根据特征图上某个像素的合集作为输入自动生成Involution Kernel。Involution Kernel 表示为，其中：φ2是由两层线性变换中间夹杂批标准化（Batch Normalization，BN）和修正线性单元（Rectified Linear Unit，ReLU）的操作，Ψi，j是输入特征图坐标（i，j）邻域的一个索引集合。因此表示输 入特征 图上包含的某个 像素合 集。Involution Kernel 的输入是特征图上（i，j）位置节点沿时间通道的一个特征向量。由于Involution Kernel 是某个通道上的特征向量，需要对它进行一个重排列转换为空间维度，生成对应的Involution Kernel，如 式（5）、（6）所 示。最后将Involution Kernel 和输入的特征图进行Multiply-add 操作以生成对应更高层次的交互特征，如式（7）所示。

其中：φ3(·)由W1和W0两层线性变换和σ2函数组成，σ2=ReLU(BN(·))代表BN 和ReLU 操作；k为通道编号；ΔK为以中心像素(i，j)进行卷积的邻域偏移量集邻域的偏移量为Involution的分组操作。

在得到高层次交互Ispa的基础上，可以得到稀疏交互作用的掩码Mspa：

其中：F{·}表示等式成立输出为1，否则输出为0；ε越大，行人之间交互作用越稀疏，反之，表明行人之间的交互作用越密集。

为了确保节点自连接，添加了一个单位矩阵Iidentity与稀疏交互作用掩码Mspa相加，得到的结果与表示交互作用得分矩阵的Rspa相乘，最后得到稀疏空间邻接矩阵：

其中：⊙为哈达玛积。

为了得到最终的稀疏空间有向图，把式（9）得到的稀疏邻接矩阵通过Zero-Softmax 函数激活，得到归一化的邻接矩阵结合空间图的节点Vt可以得到稀疏空间有向图G=。具体过程图3 所示。

2.1.4 稀疏时间有向图

对于稀疏时间有向图的生成，其生成部分与稀疏空间有向图类似，不同的地方是在时空融合部分，空间有向图沿时间通道进行了1× 1 的卷积融合，对于时间有向图，则没有这个操作，是因为行人的数量N会随着场景的不同发生改变，只需要在时空融合部分直接使用多头软注意力产生的行人运动趋势得分矩阵Rtmp，同稀疏空间有向图对Rtmp进行处理，得到表示行人运动趋势特征的邻接矩阵

如同稀疏空间有向图，从输入的时间图中获得了稀疏时间有向图以此来表示行人的运动趋势。

2.2 轨迹表示和预测

非欧数据节点的邻居节点数量可能不同，由于它不具备平移不变性，因此不能用CNN 提取图像中相同的结构。因此本文采用GCN 对稀疏空间有向图和稀疏时间有向图中的节点进行聚合，以此学习轨迹特征。使用两个GCN 对稀疏空间有向图和稀疏时间有向图进行处理：一个是先把送入GCN，然后把送入GCN；另一种方式与此相反。具体表示如式（10）～（11）：

其中：δ为参数修正线性单元（Parametric Rectified Linear Unit，PReLU）激活函数；Wspa和Wtmp是GCN 的权重；YITF表示交互-运动趋势特征，YTIF表示运动趋势-交互特征。

TCN 拥有大规模并行处理的特点，在训练和验证网络时更快，并且在处理历史信息长短问题上更加灵活，同时TCN不存在梯度消失和梯度爆炸的问题。TCN 中同时融合YITF和YTIF，在考虑行人之间的交互特征的同时，综合行人的运动趋势特征，以找到行人运动状态发生变化的关键点，从而能够更好地预测行人轨迹。因此，在时间维度上采用TCN 预测双高斯分布参数，具体表示如式（12）：

模型的训练的损失函数采用负对数似然函数：

3 实验与结果分析

3.1 数据集和评价标准

为验证本文算法的有效性，在ETH（Eidgenossische Technische Hochschule）［25］和UCY（University of CYprus）［26］数据集上进行训练。ETH 包含2 个名为ETH 和HOTEL 的场景，UCY 包含3 个名为ZARA1、ZARA2 和UNIV 的场景，每0.4 s 对数据集中的轨迹采样1 次。本文算法的训练方法与SSTGCNN 相同，在特定场景的一部分上进行训练，在其余部分上进行测试，并在其他4 个场景上验证。在评估时，观察8帧、3.2 s 的轨迹，并预测之后4.8 s 的轨迹，即12 帧图像中行人的轨迹。

采用平均位移误差（Average Displacement Error，ADE）［27］和最终位移误差（Final Displacement Error，FDE）进行度量评估。ADE 测量所有的预测轨迹点与真实轨迹点的均方误差，FDE 测量预测目的地和真实目的地的距离误差。具体计算方式如式（14）～（15）所示：

3.2 实验参数设置

在实验中，设置图形嵌入维数为64；多头软注意力层数为1；内卷网络的通道维度为64；卷积核大小为3；步距为1；内卷网络层数为1。空间-时间图卷积和时间-空间图卷积分别级联1 层、TCN 级联5 层。非线性激活函数δ采用PReLU［28］。使用Adam［29］优化器训练150 个epoch，数据批次大小为128，初始学习率为0.01，衰减系数为0.000 1，以50个epoch 为间隔。在推理阶段，从学习的双变量高斯分布中抽取20 个最接近地面真实的样本计算ADE 和FDE 度量。

3.3 实验结果

将本文算法与S-LSTM、S-GAN、SoPhie、PITF、GAT、SBiGAT、SSTGCNN、RSBG、STAR、SOPM、SA-GAN、TP-GCN、SGCN 进行实验比较。实验结果如表1 所示，可以看出，本文算法优于对比算法，尤其是FDE。相较于SGCN，本文算法的FDE 降低了16.92%；相较于SOPM，本文算法的ADE 降低了2.78%。通过分析发现，使用MS ATT 能有效捕获行人之间有意义的位置交互信息，同时采用Involution 捕获了同一时间单个行人与全局行人交互对行人轨迹预测的影响，因此可以得到更好的预测效果。

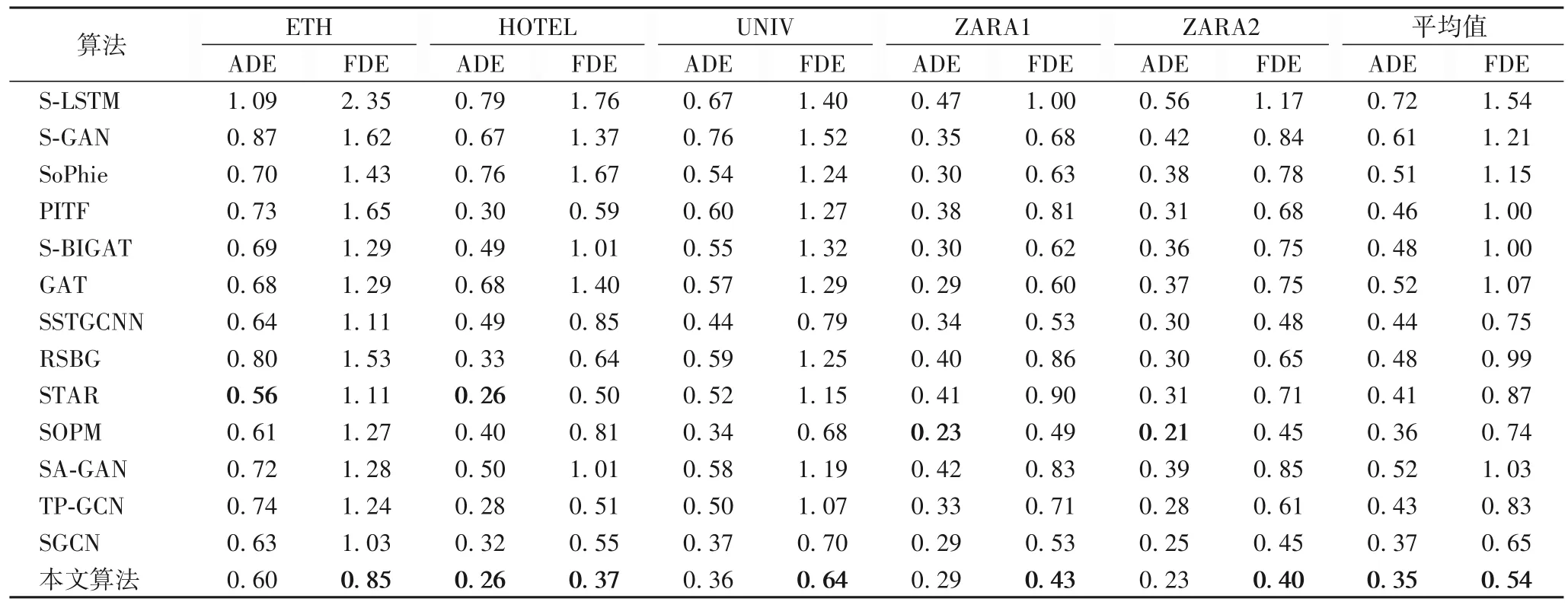
表1 不同算法的ADE、FDE指标对比Tab.1 ADE，FDE indicators of different algorithms

在算法模型训练期间，记录并绘制了本文算法的最小训练损失和验证损失随迭代次数变化的曲线，如图4 所示。

图4 训练损失与验证损失Fig.4 Training loss and validation loss

将本文 算法与S-LSTM、SR-LSTM［30］、S-GAN、PITF、SSTGCNN、SGCN 进行对比，算法参数量和推理时间结果如表2 所示，实验的推理时间为每个推理步骤所用时长之和。实验结果表明，相较于SGCN，本文算法在推理时间相同的情况下，参数量减少了28.32%；相较于PITF，本文算法的参数量减少了94.95%，推理时间减少了97.38%。虽然本文算法的参数量和推理时间都高于SSTGCNN，但ADE 和FDE 都小于SSTGCNN。

表2 算法参数量和推理时间Tab.2 Parameters and reasoning time of algorithms

3.4 消融研究

为验证算法模块的有效性，在ETH 和UCY 数据集上进行了消融实验，以分离每个模块对最终性能的影响。如表3所示，本文评估了MS ATT 与Involution 模块。可以看出，只使用MS ATT，相较于同时使用MS ATT 与Involution 的本文算 法，ADE 提高了2.78%，FDE 提高了10.00%，验证了Involution 对行人轨迹预测的贡献。只使用Involution，ADE提高了2.78%，FDE 提高了8.48%，表明多头软注意力对行人轨迹预测也很重要。无论去除哪个模块都会导致网络的准确率降低。实验结果表明，稀疏内卷学习的多头软注意力和内卷网络对行人轨迹预测很重要。

表3 不同模块的消融实验结果Tab.3 Ablation experimental results of different modules

为了验证行人之间交互作用的稀疏性对行人轨迹预测的影响，本文设置了不同大小的ε来寻找合适的阈值，具体如表4 所示。ε=1，表示行人之间没有交互作用；ε=0，表示行人之间有非常密集的交互作用。ε越大，行人之间交互作用越稀疏；ε越小，行人之间的交互作用越密集。可以看出，当ε=0.5 时，本文算法具有最佳的预测效果。

表4 不同ε阈值的消融实验的ADE/FDE指标Tab.4 ADE/FDE indicators of ablation experiments of different ε

3.5 可视化绘制和表示

对于实际场景下轨迹预测的绘制，需要将预测坐标点转换为像素坐标点。具体做法如下：1）使用OPENCV 每0.4 s对视频数据集进行采样，将视频转换为帧；2）输出感兴趣的预测轨迹，在文本数据集下找到对应的帧ID，从对应帧ID 到OPENCV 处理好的视频帧下找到对应帧；3）对感兴趣的预测轨迹点进行单应性变换为像素坐标点，绘制到对应的图像帧。图5 为直接使用预测的行人坐标点绘制的行人轨迹。

图5 同时对比了三组不同的场景：图5（a）、（b）表示两个行人向相同方向行走，图5（c）表示三个行人并排行走。实心圆点代表预测的起点，虚线代表预测的轨迹，实线代表真实的轨迹，不同标记的轨迹代表着不同的行人。在图5（a）中，本文算法的FDE 最优；在图5（b）中，SSTGCNN 预测的行人i的ADE 和FDE 都达到了最优，行人j的FDE 最优；图5（c）中本文算法的FDE 同样取得了最优。

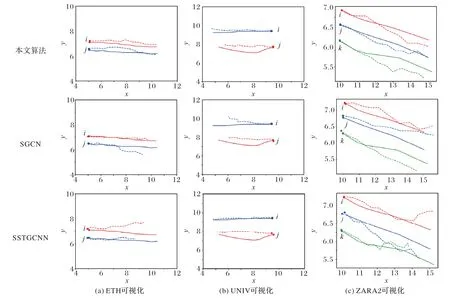
图5 轨迹可视化表示Fig.5 Visual representation of trajectories

图6 为ETH、HOTEL 实际场景下部分轨迹预测的可视化表示，将本文算法、SGCN、S-LSTM 的预测轨迹和真实轨迹进行对比，图中圆点代表行人当前位置。图6（a）中，S-LSTM 拟合效果最优。图6（b）、（d）、（e）中本文算法的拟合效果最优。图6（c）中，本文算法和SGCN 都能够很好地拟合真实轨迹，S-LSTM 的拟合较差。图6（f）中3 种算法都能够较好地拟合真实轨迹。图6（g）～（i）展示了相向行走的行人受对面行人的影响，可以看出，本文算法的拟合较好。综上所述，本文算法预测的轨迹更加贴合行人的真实轨迹。

图6 实际场景可视化表示Fig.6 Visual representation of actual scenes

4 结语

本文提出多头软注意力生成行人之间的交互得分矩阵，以捕获同一空间位置下有意义的位置交互信息；并设计了一种稀疏内卷学习网络以模拟稀疏有向交互和运动趋势，在ETH 和UCY 数据集上的结果均优于对比算法。现有方法并未考虑场景因素给行人轨迹预测带来的预测影响，因此在轨迹预测方面仍有提升空间。在今后的工作中，将研究如何有效融合场景因素以进一步提升行人轨迹预测的精度。