基于循环神经网络的人体运动模型的隐状态初始化方法

李南帆，司文文，杜思远，王志勇，钟重阳*，夏时洪

（1.国网北京城区供电公司，北京 100034；2.中国科学院计算技术研究所，北京 100190；3.中国科学院大学，北京 100049）

0 引言

人体运动合成是计算机图形学中的重要问题，在自动驾驶、人机交互、目标追踪、运动规划、动作识别等领域被广泛应用，为这些应用提供数据支撑。动作识别方法［1］在实际生活中有着重要的应用价值，它能自动识别人的动作类型，帮助系统对行人进行安全监测。基于神经网络的动作识别模型的性能相较于传统的统计学习方法有了很大的提升，但是它的准确率和效率严重地依赖人体运动数据的数量和质量。由于传统的运动捕获方法费时费力，越来越多的学者开始研究如何自动高效地捕获人体运动数据［2-3］。其中一种高效且低成本的方式就是利用已有的运动捕获数据，构建生成模型以自动合成运动数据。不仅能提高运动捕获数据的利用率，还能合成很多难以捕获的人体运动，为识别算法提供数据支撑，提高识别准确率，减少运作成本。

近年来，研究者们［4-8］使用循环神经网络（Recurrent Neural Network，RNN）进行人体运动建模与合成，并取得了较好的效果。然而，基于RNN 的人体运动模型一直都存在一个问题：运动合成结果的第一帧与输入的最后一帧之间存在跳变［4-5，7-8］。如图1 所示，圆圈中的膝关节和颈关节在输入末帧与合成首帧之间存在不连续现象。由于该问题只存在于运动合成的第一帧，很多研究者忽略了这一问题。但是首帧跳变不仅影响运动合成的质量，而且无法回避运动去噪、运动插值等应用。因为RNN 模型在进行运动合成时，首帧的隐状态通常初始化为0 或进行随机初始化，然而隐状态代表了RNN 单元对前面序列的记忆，理论上应该与前面的运动序列相关，正是这种简单的初始化方法导致了跳变的出现。虽然训练数据足够充分和多样时，跳变的影响会得到缓解，但是高质量的运动数据的获取费时费力、成本高昂。

为合理估计隐状态，在数据有限的情况下合成高质量的数据，为数据驱动的模型提供数据支撑，本文解释了基于RNN 的人体运动合成中输入末帧与合成首帧之间存在跳变的原因，提出一种基于优化的初始隐状态估计的人体运动合成方法。将初始隐状态作为自变量，利用神经网络的目标函数作为优化目标，使用梯度下降法进行优化求解，得到一个合适的初始隐状态，可提高运动合成结果的质量和运动预测的精确率。为验证本文方法的效果，在常用数据集CMU（http：//mocap.cs.cmu.edu/）和H3.6m（http：//vision.imar.ro/human3.6m/description.php）上进行大量的定性和定量实验，并且和经典的运动合成与预测工作进行对比。实验结果表明，经过初始隐状态估计的运动合成方法消除了以往基于RNN 的运动模型中输入末帧与合成首帧间的跳变情况，得到了更连续、自然的运动，有效提高了合成运动的质量。

1 相关工作

随着深度学习的兴起，很多工作集中于使用深度神经网络建模人体运动中的动态，实现对人体运动的合成和预测。

Holden等［9-10］尝试了其他类型的神经网络进行人体运动建模：1）在一个很大的数据集中训练了一个卷积自编码器，然后用卷积神经网络建立一个从高层参数到角色运动的回归模型。该方法适用于运动编辑，但是不能建模运动的分布，并且需要使用方波生成步态信息，受到的限制较大。2）建立了一个根据相位改变网络参数的三层神经网络，结合历史运动轨迹和当前的控制输入实时合成当前帧的运动姿态。Zhang等［11］使用混合权重的神经网络模型处理四足动物的运动建模与在线控制问题。上述模型虽然能够对控制作出响应，但是实质上仍然不是生成式模型，并且不能预测运动的分布。虽然基于其他神经网络的方法在人体运动合成方面作出了有益的尝试，但是由于RNN 在处理时序序列上的优势，目前RNN 仍是主流的人体运动合成模型。

RNN 能够处理时序动态关系和长时间的时序依赖关系，能够很好地建模人体运动的动态。Fragkiadaki等［4］引入LSTM-3LR（3 层的长 短期记 忆（Long-Short-Term-Memory，LSTM））和编码器-循环-解码器（Encoder-Recurrent-Decoder，ERD），利用LSTM 单元建模人体运动的动态。Jain等［5］引入结构化的RNN 模型，将人体关节的图结构与人体运动的序列关系一起引入运动预测。除了在运动预测方面的应用外，Harvey等［12］使用RNN 和半监督学习帮助训练运动分类器，成功地在半监督的条件下利用运动合成结果辅助进行运动分类。

然而，现有的RNN 模型往往在合成长时间的运动时遇到困难。在生成长序列运动时，由于每一帧的误差不断累积，模型的误差会不断变大，并终止于平均姿态。此外，大多数RNN 模型都会遇到合成首帧与输入末帧不连续的问题。Martinez等［6］提出残 差门控 循环单 元（Residual Gate Recurrent Unit，RGRU）模型，使用一个基于残差的序列到序列的方法减小了跳变；但是基于残差的方法会影响系统的稳定性，导致以上方法并不能生成很长的运动序列。Zhou等［8］成功地训练了一个自适应的RNN 模型，能够生成很长的运动而不出现崩溃；但是该模型在初始帧处理中与传统的RNN 模型相同，依然会在输入的最后一帧与合成的第一帧之间出现跳变。Lee等［13］将控制参数加入运动表示，实现了可控制的运动合成；然而控制参数的引入也无法解决首帧跳变的问题。

上述工作要么忽视了首帧跳变的问题，要么在训练时采用一些技巧回避该问题。只有Wang等［14］在构建基于RNN的人体运动模型时提到了首帧跳变问题，但是缺少详细分析。本文将分析传统的基于RNN 的人体运动合成模型首帧跳变问题产生的原因并给出解决方案，通过优化的方法求解合理的初始隐状态，有效减少首帧跳变，最后通过实验验证该方法在运动合成、运动预测和运动插值任务中的有效性。

2 本文方法

2.1 RNN人体运动建模简述

在使用神经网络模型建模人体运动之前，需要把人体运动表示为计算机能够理解的特征信号，在定义好运动表示后再针对人体运动的特点建立对应的合成模型。

2.1.1 人体运动表示与特征表示

本文使用的骨架包括18 个自由运动关节，可表示为：

其中：q为角色的关节角运动参数；tx、ty、tz是根节点的位置；rx、ry、rz是根节点的旋转角度；θ2，θ3，…，θd是其他各个关节的三维旋转角度。人体运动建模中使用的特征需要具有旋转不变性和平移不变性，所以更改为如下表示：

其中：x为具有旋转不变性和平移不变性的运动参数；Δtx、Δtz、Δry是相较于前一帧的相对平移和旋转；其他变量的定义方式与式（1）相同。

2.1.2 RNN人体运动模型

本文创新点在于初始隐状态问题的发现与相应估计方法的提出，该方法能够应用于任意的RNN 模型。因此本文通过改进经典的运动合成模型ERD 以验证方法的有效性，改进的运动模型如图2 所示，（·）为该网络层神经元个数。

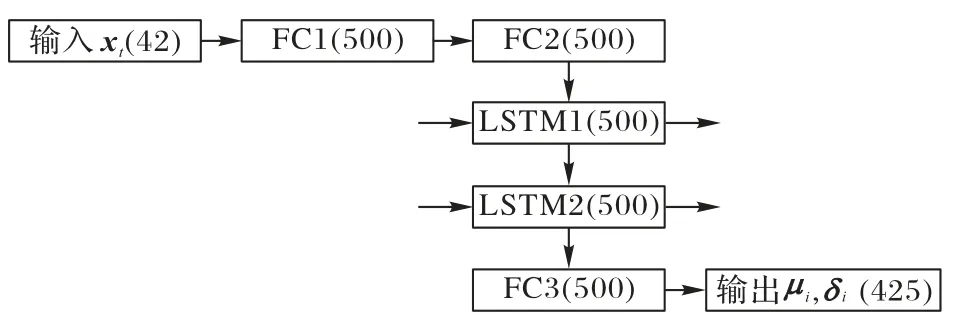
图2 运动模型结构Fig.2 Structure of motion model

本文采用的RNN 模型包含两层全连接（Fully-Connected，FC）-两层LSTM-两层全连接的编码-解码结构。与ERD 不同，它能建模人体运动参数在下一帧的分布，因此可以用于多种任务，数学表达形式为：

与文献［15］类似，本文使用协方差矩阵为对角矩阵的高斯混合模型（Gaussian Mixture Model，GMM）建模下一帧的特征分布，混合高斯分布的定义为：

其中：wi、μi、δi分别为第i个高斯分量的概率、均值和标准差。高斯分布的参数需要满足一定条件，而神经网络的输出可以是任意实数。所以本文定义以下的变换以保证得到的参数符合高斯分布的定义：

在模型训练完成后，通过如下方式实现运动生成：用户提供若干帧的运动数据作为初始输入，将当前帧运动数据和上一帧的隐状态作为RNN 单元的输入，RNN 单元经过计算得到当前帧的隐状态和下一帧的运动参数分布；从这个分布中进行采样，可以得到下一帧的运动参数；重复这一过程，就可以逐帧地合成一个无限长的运动序列。

生成式模型得到的并不是下一帧运动参数的准确值，而是对下一帧运动参数的分布的估计，所以模型并不能直接应用于运动预测问题。在进行运动预测实验时，本文使用概率最大的高斯分量的平均值作为下一帧的运动预测值，然后将这个运动预测结果输入神经网络，从而得到运动预测结果。

2.2 首帧不连续问题分析

基于RNN 的人体运动模型中的首帧跳变现象如图1 所示。出现首帧跳变现象的原因是在训练中RNN 模型会将上一帧的运动参数和上一帧学习到的隐状态作为RNN 模型当前帧的输入，将下一帧的运动参数作为目标输出以进行训练。模型训练目标表示为式（6）。一般输入隐状态包含对以前状态的正确的记忆，非零。然而在计算首帧运动参数时，神经网络无法从前一帧得到隐状态，只能使用零初始隐状态或随机初始化的隐状态作为输入，得到的概率值为：

这样的初始输入与训练时不一致，将导致输出的第一帧与输入的最后一帧之间出现明显跳变，这也是在实验中往往会发现模型在运动合成开始处出现不连续现象的原因。

文献［4-5，8］中均指出了这个问题，但是认为首帧跳变在运动合成和预测任务中可以接受，因此选择忽略这个问题。然而本文的研究表明，估计一个更好的初始隐状态可以提高运动合成的质量，并降低运动预测的误差。同时，当基于RNN 的人体运动模型被应用到运动去噪或者运动插值任务中时，首帧跳变问题的影响会被放大。例如，在运动去噪中，由于首帧跳变，即使去掉第一帧运动，后续的运动去噪结果与输入运动仍存在一定差异，不能达到运动去噪的目的；在运动插值中，用户给定运动序列中的若干关键帧，要求算法自动合成各个关键帧中间的运动，首帧跳变会导致运动插值结果不够自然。基于上述原因，首帧跳变问题无法回避。

目前已经有一些方法来解决该问题，如基于序列到序列的RGRU 模型［6］采用残差连接的方法使模型在零初始隐状态下也被充分训练，但是有两个局限性：1）只能用于无约束的运动合成，无法用于运动插值、运动去噪等应用；2）序列到序列的模型只能合成一定长度的运动，无法保证训练得到的模型能够合成无限长的运动。这些方法本质上是一种训练的技巧，没有从原理层面解决这个问题。还有一些方法采用预训练的方式，先训练一个基本模型，然后进行最终调整（Fine-tune）。然而这些方法并不适用于初始隐状态估计的问题。因为隐状态是一个RNN 单元的输入，而不是参数，预训练并不能得到合适的隐状态。无论是否进行预训练，RNN模型在实际测试时，都需要给定一个初始隐状态作为第一个RNN 单元的输入，想要得到一个合理的非零的隐状态，必须要进行隐状态估计，而不是简单地置零或者随机初始化。

2.3 初始隐状态估计方法

为了解决人体运动建模中的首帧不连续问题，需要给出一个对神经网络初始状态的估计。本文提出从RNN 运动模型的定义出发，使用第一帧隐状态对应的高斯似然估计，利用神经网络的误差函数来度量隐状态的合理性：

其中：P(xi|xi-1，hi-1，ci-1)是式（7）中描述的高斯混合模型；n表示输入运动的长度。

如图3 所示，本文将h1和c1视为自变量，通过优化h1和c1以最大化式（8）中的概率P。因此需要找到一个隐状态h1和c1，在这个隐状态和用户给出的第一帧运动的条件下，指定运动输入的剩余部分出现的概率最大。

图3 隐状态估计模型Fig.3 Hidden state estimation model

本文将上述问题作为一个优化问题来求解。该问题的导数的推导方式与神经网络相同，只是自变量从网络各层的参数w和b变成了神经网络在初始时刻的因变量h1和c1。图3 用虚线框出的h1和c1是本文需要求解的初始隐状态，x1，x2，…，xn为输入运动序列。本文使用梯度下降的方法求解这个问题，方法步骤如下。

步骤1 首先把初始隐状态初始化为零状态。

步骤2 利用当前隐状态对神经网络进行正向传播，更新y1，y2，…，yn-1。

步骤3 将-lnP作为损失函数，求出损失函数的值，并进行沿时间的反向传播［16］，得到导数

步骤4 利用得到的导数更新h1和c1的值其中：lr是梯度下降法的步长。如果损失函数已经收敛，那么迭代结束，并将得到的h1和c1作为运动合成中使用的初始隐状态；否则回到步骤2。

本文成功地通过该方法找到了合适的初始状态，使神经网络模型对各帧的运动参数分布预测的均值与实际的用户运动输入非常接近，保证了在运动输入末帧与运动合成首帧之间的连续性。同时，由于本文方法具有一个更合理的初始隐状态，预测结果也比传统的零初始隐状态方法更准确。

3 实验与结果分析

为了验证本文的初始隐状态估计方法能够提升运动模型的性能，从运动合成、运动预测和运动插值三个方面进行实验，实验结果表明本文方法能够提高运动合成质量和运动预测精度，还能得到真实自然的运动插值效果。

3.1 实验设置

为验证本文方法的有效性，将本文方法与经典的运动模型ERD 和RGRU 进行比较，在CMU 和H3.6m 数据集上进行定性和定量实验。实验中，学习步长取0.002，最大迭代次数取1 000，网络结构中FC1、FC2、LSTM1、LSTM2、FC3 的神经元个数均设为500，模型在NVIDIA GTX 1080 上运行。

在运动合成实验中，本文使用相同的随机数，把3 帧运动作为输入，使用ERD 和本文方法分别进行运动合成；在运动预测实验中，将运动的前几帧作为输入，随后分别测试ERD、RGUR 和本文方法的误差结果，以度量本文方法的准确性；同时进行运动插值实验以验证本文方法能够针对给定的运动首末帧生成一段完整的运动。

3.2 运动合成实验

图4 为运动合成实验的可视化结果。前3 帧为输入的运动，后5 帧为合成的运动，将运动不连续现象用圆圈标出。可以看出，本文方法明显合成了更自然的运动，消除了首帧的不连续现象，并且后续的合成帧也受到了第一帧的影响。这种影响在后续的运动预测实验中将体现得更加明显。

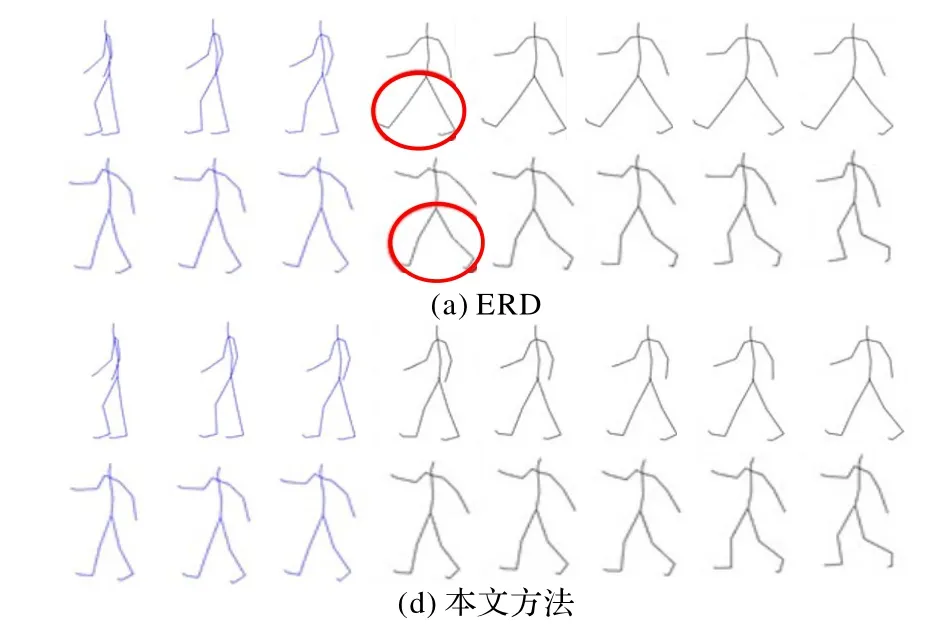
图4 运动合成结果比较Fig.4 Comparison of motion synthesis results

图5（a）绘制了脚踝关节点的z方向速度曲线。可以看出，经过本文方法的初始隐状态估计的结果明显更加平滑。同时，为了验证本文方法能够消除神经网络隐状态在运动起始阶段的跳变，使用相同的随机变量，对使用CMU 运动数据库训练得到的运动模型进行采样，隐状态值如图5（b）所示。可以看出本文方法得到的曲线更加平滑，而ERD 得到的曲线在起始帧存在一个跳变。这也验证了在2.2 节中提出的理论：运动隐状态一般情况下都不会恰好为0。以往的运动模型在运行中从零隐状态出发，对于人体运动合成模型本身也不合适。通过估计一个初始隐状态，本文不但从输出的运动姿态层面得到了一个更好的首帧合成结果，而且使RNN模型本身也得到了更加连续的隐状态。

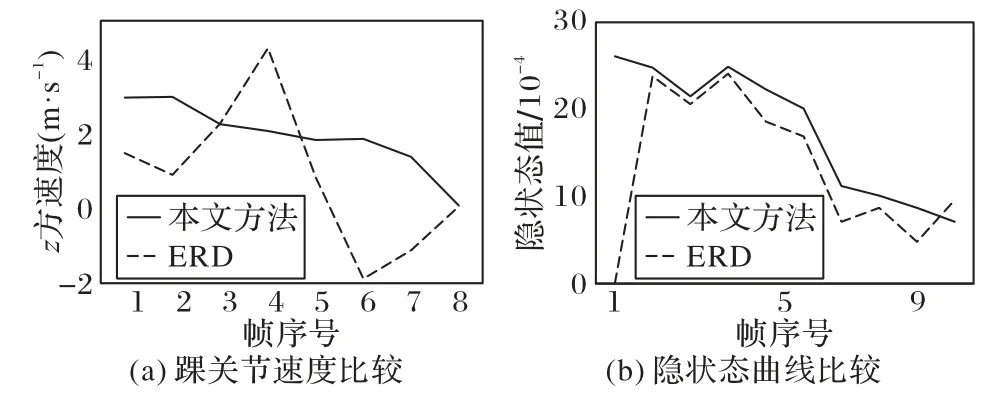
图5 踝关节速度与隐状态比较Fig.5 Comparison of ankle joint velocity and hidden state curves

3.3 运动预测实验

本文在H3.6m 数据集上进行运动预测实验，与之前的研究［4-6］使用相同的训练数据集和测试数据划分方法。运动预测的评估标准是预测结果和真实值的误差大小。将本文方法在走路运动中的预测误差和ERD、RGRU 进行了对比，如表1 所示。实验结果表明本文方法的首帧运动预测结果误差更小，相较于ERD 的预测结果，在第1 帧上的误差减小了63.51%；相较于RGRU，在第1 帧的误差减小了6.90%。并且因为第1 帧的误差减小，导致后续的运动预测误差也更小，在10 帧上的总误差相较于ERD 和RGRU 减小了50.00%、4.89%。本文方法不仅能够显著降低模型的第一帧运动预测的误差，还能降低总体的运动预测误差。

表1 走路运动的关节角预测误差比较Tab.1 Comparison of joint angle prediction errors for walking motion

图6 为本文方法和ERD 的运动预测的可视化比较结果，图中实线框内的3 帧为给定的运动输入，虚线框内的5 帧为运动预测结果。可以看出，本文方法的预测结果很好地缓解了首帧跳变问题，更接近真实运动。

图6 运动预测结果比较Fig.6 Comparison of motion prediction results

3.4 运动插值实验

由于首帧跳动变，文献［4-5，7，17］中的方法都无法用于运动插值问题；而文献［6］中的方法虽然避免了跳动，但是这种方法要求一个运动序列作为输入，在运动插值问题中往往无法满足；本文方法可以很好地用于运动插值任务。

运动插值问题的输入是首帧和末帧的运动姿态和位置，要求合成中间的运动。与传统运动插值方法不同，本文在最大后验概率的框架下，利用运动模型作为先验来优化求解最适合的运动，使运动合成结果保持自然的同时，尽可能地符合给定的运动输入。优化问题的误差函数可以写成：

其中：第1 项是运动先验项，度量得到的运动是否满足运动模型建模，与式（6）完全一致；第2 项是拟合项，度量得到的结果是否符合指定的运动首末帧。该拟合项可以表示为：

其中：Pn是给定的末帧关节点位置；pn是优化得到的末帧关节点位置。插值结果如图7 所示，首帧和末帧的姿态用实线框出，虚线框中的姿态对应运动插值，图中每隔4 帧显示1帧。实验结果表明，本文方法可以很好地应用于运动插值问题，能够解决以往基于RNN 的方法都无法解决的问题。

图7 运动插值结果Fig.7 Motion interpolation results

4 结语

针对基于RNN 的人体运动模型中首帧跳变的问题，本文分析了问题产生的原因，并通过估计RNN 模型的初始隐状态，成功地解决了RNN 模型的首帧跳变问题，并在运动合成、运动预测和运动插值任务上进行大量实验。实验结果表明，本文方法在运动合成任务中得到了连续、自然的运动合成结果；在运动预测问题中得到了更准确的运动预测结果；在运动插值任务中，解决了其他基于RNN 的模型无法解决的插值问题。本文主要研究人体运动合成中的首帧跳变问题，原理上并不依赖于使用的网络模型结构，所以任何基于RNN 的运动模型都可以通过引入本文的初始隐状态估计方法得到更好的运动合成质量和更精确的运动预测结果。

本文方法虽然在实验中始终有效，但还无法从理论上保证得到的初始隐状态始终合理，求出的隐状态有可能并未在训练中出现，导致运动合成结果不自然。而且本文方法只适用于逐帧运动合成的网络结构，并不适用序列到序列的模型。