风电场并网振荡的频域网络分析及抑制
朱克平,何英静,但扬清,李 倩,曹建春,宗皓翔
(1.国网浙江省电力有限公司经济技术研究院,杭州 310008;2.中电普瑞电力工程有限公司,北京 102200)
随着“碳达峰、碳中和”能源转型战略的提出[1],以风电为主要代表的新能源发电在我国得到长足发展。但是,随着风电并网规模的不断扩大,以宽频振荡为特征的小扰动失稳问题[2-3]日益突出。为此,有必要对风电场并网系统的振荡问题进行全面分析,以保障系统的安全、稳定运行。
针对风电场的振荡问题研究,频域阻抗分析法[4-5]因其物理意义清晰、可扩展性强、易于测量等优点被广泛采用,其主要原理为:分别建立风电场的阻抗(Y)“荷”模型以及电网的导纳(Z)源模型,形成“源荷”闭环分析模型,通过分析阻抗比ZY环绕点(-1,j0)的情况,以此对系统稳定状态进行评估。根据风电场阻抗模型获取方式的不同,主要有3种研究思路,具体为:①采用阻抗的形式表征风电场内部的各个组成元件(风机、变压器、线路等),并根据场站拓扑形成阻抗网络,通过电路串并联运算对该阻抗网络进行化简,最终获得风场并网点处的等效聚合阻抗[6-7],例如,文献[6]给出了dq坐标下的阻抗网络形成及化简流程;②基于传统倍乘聚合原则,根据风电场的功率等级计算其单机聚合模型的电气及控制器参数,基于该单机等效模型进行风场阻抗建模[8-9],例如,文献[9]采用该方法对直驱风电场进行等效阻抗建模;③利用参数拟合等技术,基于风电场的出口频域特性反向辨识风场聚合模型,由此获得易于数值分析的等效阻抗模型[10-11],例如,文献[11]基于一种矢量拟合技术辨识双馈风电场等效模型的聚合参数,建立了能够表征场站端口频域特性的聚合阻抗模型。但是,由于所建风场阻抗模型多为聚合形式,无法反映系统完整的拓扑信息,这导致失稳要素定位较为困难。同时,上述各类针对风电场的振荡分析研究主要关注风电场并网的稳定状态(即稳定或不稳定),较少探究振荡是由何种因素导致并对其进行定位,这不利于针对性地部署振荡抑制措施。
围绕上述所存在的问题,本文致力于提出一种计及风电场网络特性的振荡失稳要素定位方法。具体包括:首先,建立风电场的完整网络矩阵模型,基于该模型对系统稳定状态进行评估并提取主导失稳模式;其次,建立节点参与因子指标以定位参与系统振荡的主导节点;进一步地,对主导节点处各元件的参数进行灵敏度分析,建立量化指标,从而确定参与系统振荡的关键参数;最后,利用所获取的主导节点、关键参数信息,指导控制器参数的调整设计,从而实现系统振荡的抑制与消除。
1 风电场频域网络建模及判稳依据
本节主要介绍了一种计及风电场详细网络拓扑的节点导纳矩阵构建方法,并基于该模型提出一种基于系统零点分布的判稳依据。首先,以直驱风机为例,简要给出了风电机组并网点处的阻抗建模。然后,基于阻抗网络理论[6],提出了风电场的频域网络建模方法,形成了包含风力发电单元、变压器、输电线路等在内的节点导纳矩阵模型。最后,基于系统零点分布,给出了小扰动失稳依据,以获取系统的主导失稳模式。
1.1 风机阻抗建模
为了便于读者理解,以直驱风电机组为例,简要介绍风机并网点处的交流阻抗建模方法。图1展示了一个典型的直驱风机拓扑,主要包括3个子系统,分别为永磁直驱发电机、机侧变流器以及网侧变流器。依次给出各个子系统的阻抗建模,最后形成交流并网点处的等效阻抗。
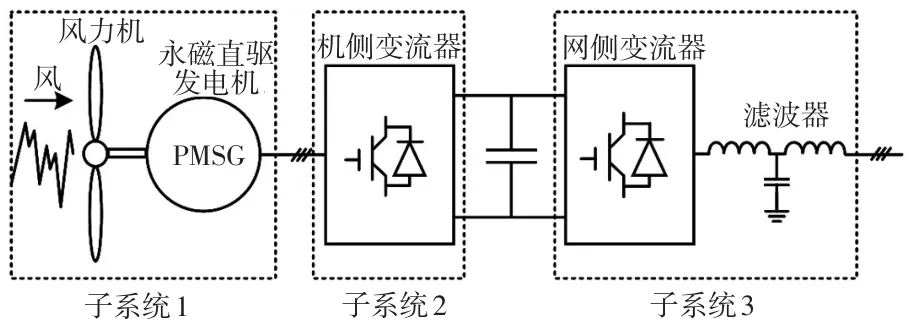
图1 直驱风电机组结构Fig.1 Structure of direct-drive wind turbine
1)永磁直驱发电机阻抗
dq坐标系下,永磁直驱发电机的小信号模型可表示为
式中:上标‘m’代表机侧变量;下标‘s’代表永磁电机定子侧变量;为永磁发电机定子dq轴电压;为永磁发电机定子dq轴电流;Lsd和Lsq分别为永磁发电机定子d轴和q轴自感;Rs为永磁发电机定子d轴和q轴自阻;ωr0为发电机电气转速的稳态值;为永磁发电机dq轴阻抗。
2)机侧变流器阻抗
机侧变流器主要控制永磁直驱发电机转矩和无功功率,具体控制结构参见文献[8],这里不再赘述。根据转矩表达式和转矩调节器,可以得到转矩环的输入-输出频域模型为
电流内环的小扰动模型为
式中:Hc(s)为电流内环的PI调节器传递函数;为机侧变换器dq轴电压;Ucd0和Ucq0为相应电压的稳态值;Udc0为直流电压稳态值;为机侧直流电压。
将式(2)代入式(3),可将机侧变流器的交流动态表征为
式中:Hc(s)为电流环PI控制器的传递函数;为交流侧动态影响;a为直流侧动态对交流侧的耦合影响。
类似地,基于交直流功率平衡,可将机侧变流器的直流动态表征为
联立式(4)和式(5),可得刻画机侧变流器交直流动态的三端口阻抗模型为
3)网侧变流器阻抗
网侧变流器主要跟踪交流电网电压,并控制直流母线电压,具体控制结构参见文献[8]。其中,锁相环小信号模型可表示为
式中:上标‘g’代表网侧变换器相关变量;Hpll(s)为锁相环的PI控制器传函;为网侧并网点处电压的q轴分量;Ug0为并网点电压稳态值;Tpll(s)为PLL闭环传递函数。
直流电压环的输入-输出频域模型可以表示为
式中:Hdc(s)为直流环PI控制器的传递函数;为网侧电流内环输入参考电流;为网侧直流电压。
网侧变流器的电流内环控制与机侧类似(式(3)所示),将式(8)所示直流动态代入可得
网侧变流器的交流滤波器小信号模型为
式中:Rf和Lf分别为网侧交流滤波器的电阻和电感;为滤波器dq轴阻抗;ω1为基频旋转角速度。
将式(10)代入式(9),可将网侧变流器的交流动态表征为
类似地,可将网侧变流器的直流动态表征为
联立式(11)和式(12),可得刻画网侧变流器交直流动态的三端口阻抗模型为
4)并网点等效阻抗建模
联立式(1)所示永磁直驱发电机阻抗、式(6)所示机侧变流器阻抗以及式(13)所示网侧变流器阻抗,消去机侧电压/电流变量以及直流侧电压电流变量[12],可得风机并网点处的dq导纳为
根据文献[13],直驱风电机组的并网稳定性由网侧变流器主导,可忽略影响较小的机侧变流器及前端系统,具体为
值得注意的是,所采用风机阻抗模型的精度,不影响本文后续系统级建模及稳定性的分析流程。
1.2 节点导纳矩阵模型
本节首先介绍了系统频域网络矩阵的构建流程,包括支路导纳矩阵、节点-支路关联矩阵以及节点导纳矩阵的形成。进一步地,还给出了一个简单网络构建样例,以便于读者更好地理解。
1)频域网络矩阵构建流程
如图2所示,典型风电场(图中以直驱风机示意)主要由风电机组、交流集线网络及接入电网组成,将各个元件的交流端口特性以阻抗形式[8]表征,可获得保留系统完整拓扑信息的阻抗网络。如第1.1节所述,可将风力发电单元交流并网点处的电压-电流输入输出关系[14]以dq轴阻抗[9]表征为
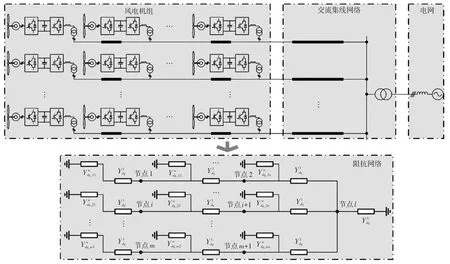
图2 典型风电场拓扑及其阻抗网络Fig.2 Topology of typical wind farm and its impedance network
类似地,还可将变压器、传输线路等无源元件[15]表征为dq轴阻抗的形式,即
例如,传输线路的dq轴阻抗可表征为
式中,Rl和Ll分别为线路的电阻和电感。
将上述各元件的阻抗/导纳按网络拓扑进行连接,即可获得系统的阻抗/导纳网络。针对这一网络的系统建模,可借鉴传统电力系统中对于网络矩阵[16]的建模方式。首先,将各个支路的导纳按对角元素形式排列,列写系统的支路导纳矩阵,具体为
式中:Ybr(s)为系统的支路导纳矩阵;Yii为支路i的dq轴导纳。
进一步地,根据网络构建原则[17],给出支路-节点关联矩阵A的构建原则,即
式中:aik为关联矩阵的内部元素;0=diag(0,0),I=diag(1,1)。
由此,可获得目标系统的节点导纳矩阵Ynode(s)为
2)简单网络构建实例
以一个3节点5支路2风机的简单场站为例,如图3所示,详细说明上述频域网络的构建流程。
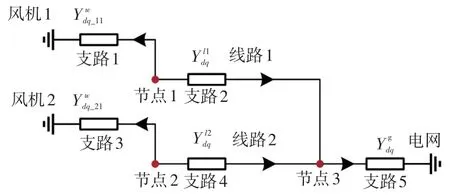
图3 简单系统拓扑Fig.3 Topology of simple system
根据图3网络拓扑,列写支路导纳矩阵为
根据图3所示支路与节点的关系,节点1是支路1和支路2的发点、节点2是支路3和支路4的发点、节点3是支路2和支路4的收点以及支路5的发点。根据式(20)所给出网络构建原则,可形成系统邻接矩阵为
将式(23)和式(22)代入式(21),可得图3所示系统的节点导纳矩阵为
1.3 基于零极点分布的判稳依据
基于上述所建立的节点导纳矩阵Ynode(s),本节给出相应的判稳方法。在电力系统中,常见的振荡失稳现象主要有2种,包括串联谐振和并联谐振。对于本文所研究的对象——风电场并网系统,其线路阻抗比(R/X)较小(即电感主导),可认为系统的串联谐振点和并联谐振点一致,分析一种情况即可[18]。
以并联谐振为例,其特点为:在节点注入较小的谐振电流即可激发较大的谐振电压。由矩阵理论可知,此时系统节点导纳矩阵接近奇异。设定系统发生频率为m的振荡,列写此频率下的节点电压V(sm)-电流I(sm)方程为
式中:Ynode(sm)为频率点m处的节点导纳矩阵;V(sm)=[V1(sm)…Vn(sm)]T,I(sm)=[I1(sm)…In(sm)]T
对Ynode(sm)进行特征值分解,可得
式中:Λ为特征值矩阵;R为右特征列向量;L为左特征行向量,满足[R]-1=L。
将式(26)代入式(25)中,可得
式中:U(sm)=[U1(sm)U2(sm)…Un(sm)]T,定义为模式电压,注意与上述节点电压V(sm)区分;J(sm)=[J1(sm)J2(sm)…Jn(sm)]T,定义为模式电流。
将式(27)以矩阵形式展开,可得
由式(28)可知,当某一特征值λi接近于0时,模态阻抗接近于无穷大,此时较小的模态电流Ji即会引发较大的模态电压Ui,可认为系统发生并联谐振[19-20]。对应到频域,需求闭环系统—节点阻抗矩阵的右半平面不稳定极点RHP-poles(right-half-plane poles),其等价于求节点导纳矩阵Ynode(s)的右半平面不稳定零点RHP-zeros(righthalf-plane zeros),表示为
因此,通过绘制节点导纳矩阵的零极点分布图,观察是否存在RHP-zeros,即可判定系统的稳定性。而所得RHP-zeros即为系统的失稳模式,实部为阻尼程度,虚部为振荡发散速率。
2 振荡失稳要素定位及抑制
基于上述所建节点导纳矩阵与所识别失稳模式,进一步给出引起振荡的失稳要素定位方法。首先,给出节点参与因子的计算方法,确定主导振荡的节点位置;进一步,给出主导节点处各元件参数的灵敏度方法,确定关键参数。由此,通过调节关键参数实现对系统失稳的抑制与镇定。
2.1 节点参与因子指标
基于式(28),将节点电压V(sm)表示为模式电压Ui(sm)的函数,即
式中,对应特征值λi=0的右特征列向量ri=[r1ir2i…rni]T刻画了振荡模式(模式电压)在各个节点(节点电压)的表现程度,即能观性。
类似地,将式(28)所示模式电流Ji(sm)表示为节点电流I(sm),即
式中,对应特征值λi=0的左特征行向量li=[li1li2…lin]T刻画了各个节点(节点电流)对于振荡模式(模式电流)的贡献/激励程度,即能控性。
将对应谐振模式的左右特征向量rili进行矩阵运算,可得节点电压-电流关系为
提取上述矩阵中的对角元素,即可获得各节点对于振荡模式的贡献程度,定义为参与因子。
2.2 参数灵敏度指标
根据节点参与因子的大小,可定位主导失稳模式的节点位置(参与因子越大,则对振荡的作用效果越显著)。进一步地,基于导数的链式法则,可获得该主导节点处各元件参数对于失稳模式的灵敏程度,定义为参数灵敏度指标。可计算任意元件α对于系统失稳模式的灵敏度为
对于位于节点i处的某系统元件α,其关于参数ρ的dq轴阻抗形式为
基于式(33),利用导数的链式法则,可进一步求取参数ρ对于系统失稳模式的灵敏度为
3 算例分析
本节考虑一个典型的直驱风电场并网系统,共包含4条馈线和8台风电机组,如图4所示。为便于后续的系统级分析,重点关注网侧变换器及其并网动态特性,忽略影响较小的机侧变流器及前端系统[21],即采用式(15)所示简化模型。值得注意的是,本文所提振荡溯源及参数定位系统分析方法,适用于各类精度的元件阻抗模型。这里仅以此简化风机模型为例,直观展示所提方法的有效性,读者可根据分析精度的需求灵活替换所采用的元件模型。
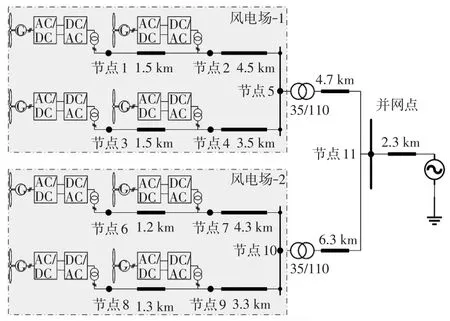
图4 风电场测试系统拓扑Fig.4 Topology of wind farm test system
上述测试系统的风机参数与集电网络参数如表1和表2所示。
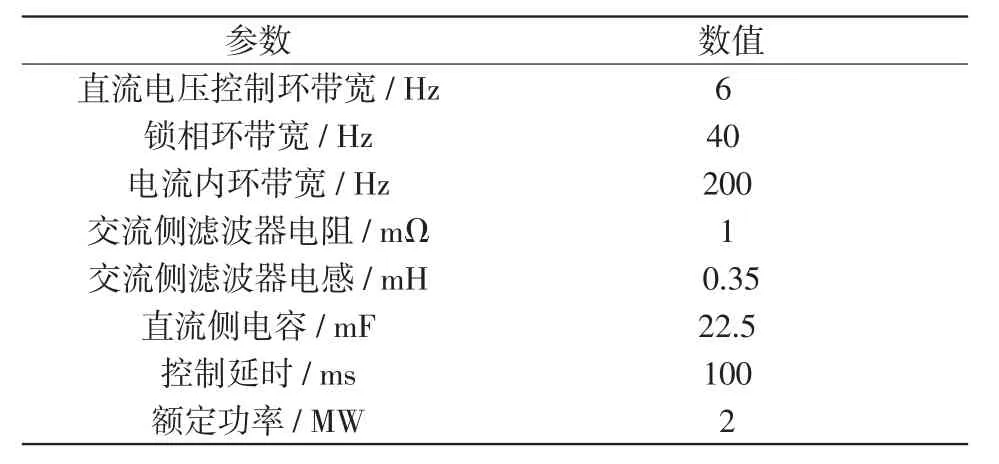
表1 风电机组参数Tab.1 Parameters of wind turbine

表2 集电网络参数Tab.2 Parameters of transmission network
3.1 系统判稳及失稳模式提取
临界失稳条件设置为将馈线3的长度由4.3 km增大至6.5 km。图5给出了时域仿真结果,系统在15 s时发生失稳振荡。
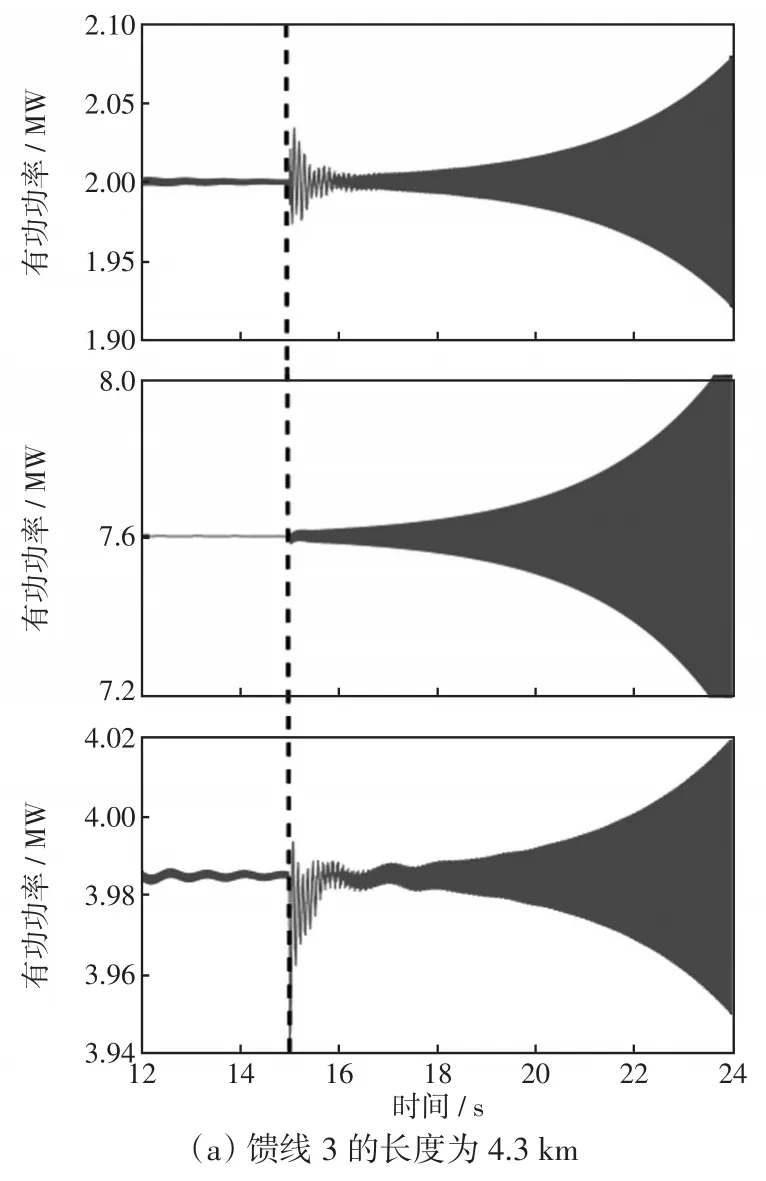
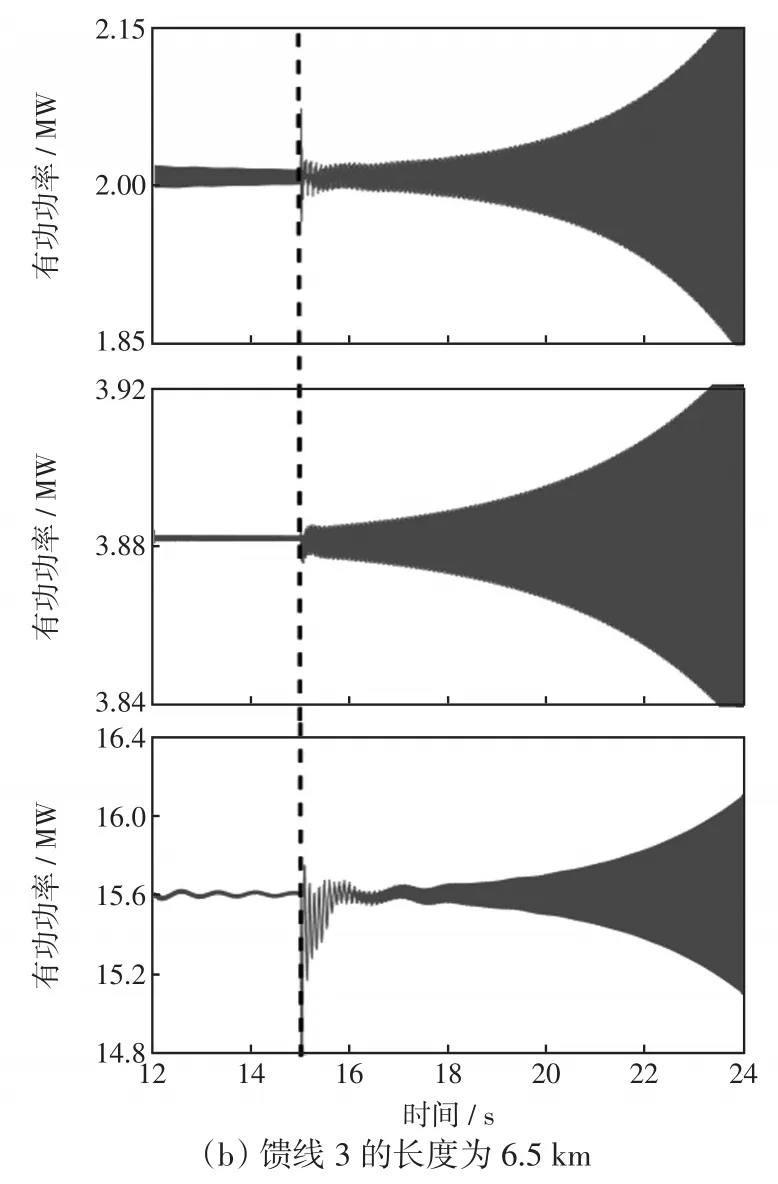
图5 时域仿真结果Fig.5 Results of time-domain simulations
对图5所示失稳波形进行FFT分析,可知失稳频率为80 Hz(dq坐标系),如图6所示。应用所提系统判稳方法,验证理论判定结果与仿真结果是否一致。
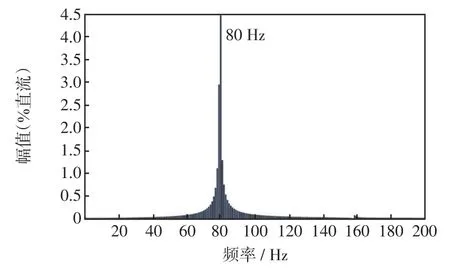
图6 FFT分析结果Fig.6 FFT analysis results
基于式(16)~(21)所给出的系统节点导纳矩阵建模方法,代入图4所示典型风电场的拓扑、参数及工作点(风机阻抗建模详见文献[8],这里不再赘述),可得目标风电场的节点导纳模型。进一步地,基于所给出临界失稳条件,绘制节点导纳模型的零极点分布,如图7所示。可以看到,系统存在一对右半平面零点,即RHP-zero。同时,虚部为495 rad/s,换算成频率即为78.78 Hz,基本与图5所示仿真结果符合,由此验证了所建立节点导纳矩阵的准确性。
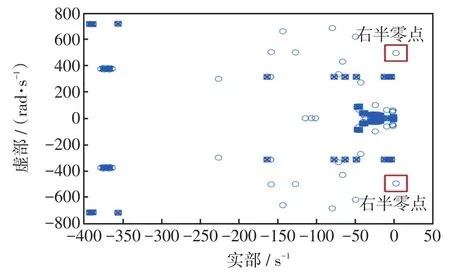
图7 零极点分布Fig.7 Pole-zero distribution
3.2 节点参与因子指标计算
基于上述建立的系统节点导纳矩阵,以及所确定的失稳模式(即右半平面零点2.9±j495),应用式(30)~(32)所示节点参与因子计算方法,求解图4中11个节点的参与因子指标。如图8所示,节点7的参与因子远大于其他各节点(≈0.422 3),因此其主导系统的失稳模式。由图4可知,节点7处主要包含1台风电机组以及馈线3处传输线路,应用参与因子指标进一步评估各元件参数的影响。
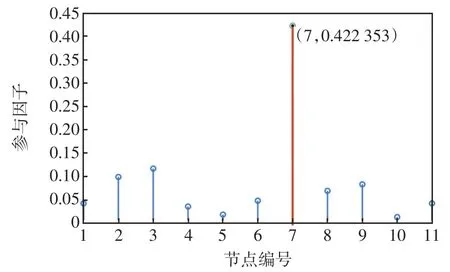
图8 节点参与因子指标Fig.8 Index of node participation factor
3.3 参数灵敏度指标计算
上述风电机组的网侧变换器参数主要包括锁相环带宽、电流内环带宽、直流电压外环带宽以及有功功率传输水平,而馈线传输线参数主要包括电阻以及电感。基于式(35)所给出的参数灵敏度计算方法,给出上述各参数的灵敏度绝对值,如表3所示。可以看到,锁相环带宽、传输线电阻和电感的灵敏度数值最大。

表3 参数灵敏度绝对值Tab.3 Absolute value of parameter sensitivity
进一步在复平面上刻画上述参数灵敏度结果,以评估其方向性。如图9所示,锁相环带宽和传输线电感的灵敏度指向右半平面,即增大会导致失稳模式向右半平面移动,从而加剧失稳;而输电线路电阻的灵敏度指向左半平面,即增大会导致失稳模式向左半平面移动,从而减轻失稳。上述参数对于失稳模式的方向性,定义为其对系统失稳模式的牵引作用。
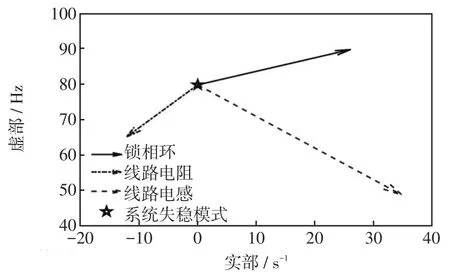
图9 参数灵敏度方向Fig.9 Direction of parameter sensitivity
3.4 系统稳定调节及验证
基于上述所得关键参数及其牵引方向,通过逆向调节即可实现提升系统稳定裕度的目标。下面分别减小锁相环带宽1%、减小传输线电感1%以及增大输电线路1%,在图5所示相同的临界失稳条件下,分别从频域零点分析和时域仿真分析两个方面,对比并分析参数调整后与参数调整前的系统稳定状态。
1)频域分析
基于上述所给出的参数调整方式,绘制系统调整后的零点分布,并与调整前的分布进行对比,如图10所示。可以看到,参数调节相同比例下,输电线路电感的作用最为明显,使得系统失稳模式向左半平面(稳定)移动最多。零点致稳效果排序为输电线路电感>锁相环带宽>输电线路电阻,这与表3和图9所示灵敏度计算结果顺序一致,验证了指标的有效性。
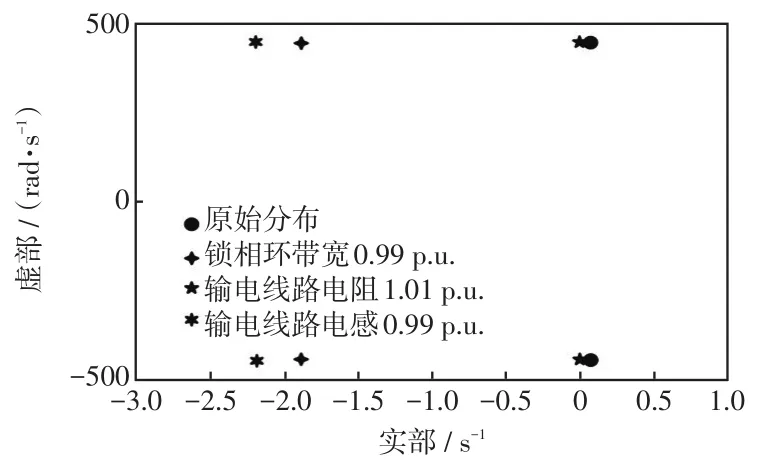
图10 控制参数调节对系统稳定性的影响(频域)Fig.10 Influence of control parameters tuning on system stability(frequency-domain)
2)时域分析
基于上述所给出的参数调整方式,给出系统的振荡波形变化情况。以节点7为例,图11给出了具体的时域仿真结果。
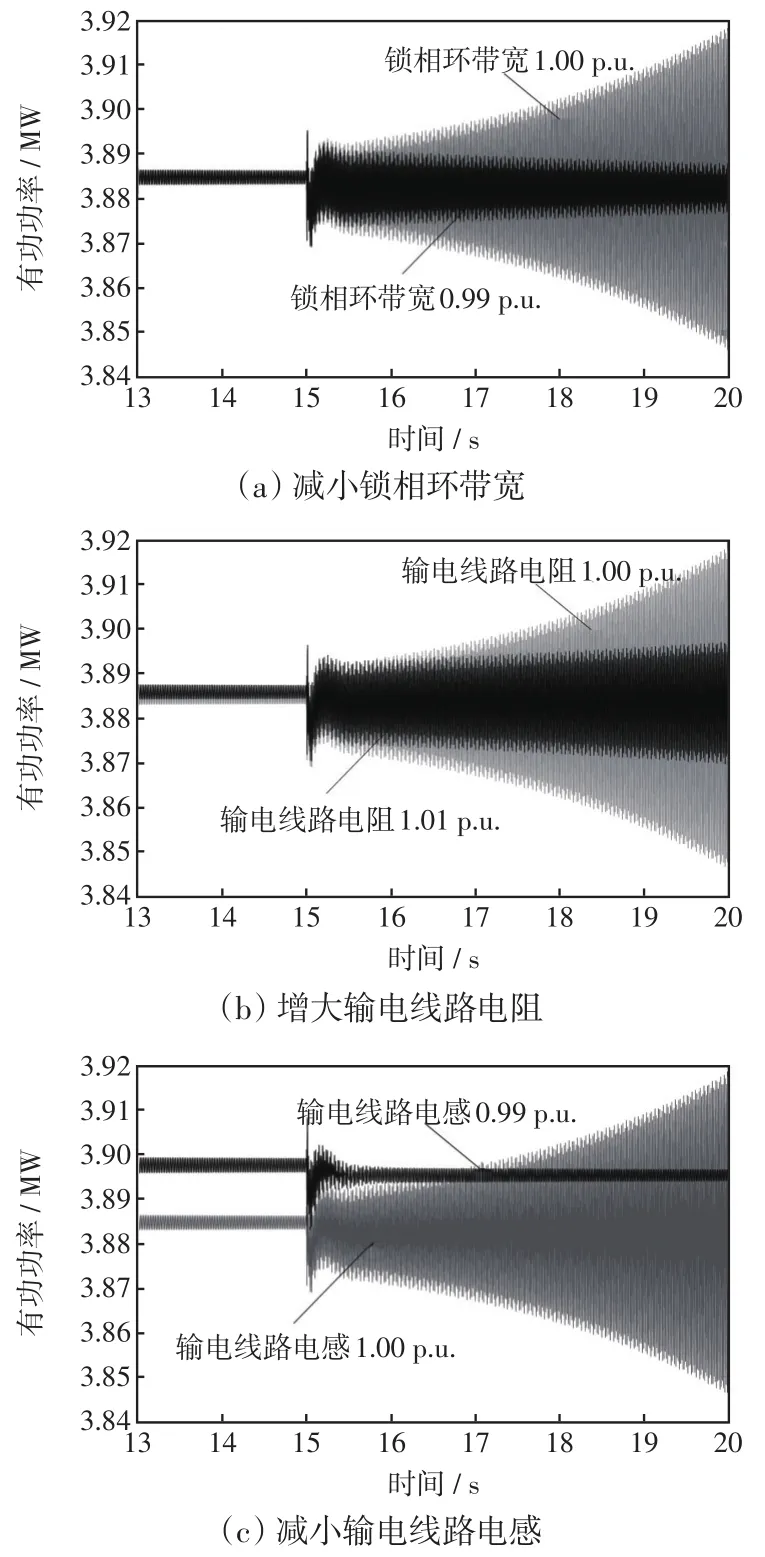
图11 控制参数调节对系统稳定性的影响(时域)Fig.11 Influence of control parameters tuning on system stability(time-domain)
通过图8可知,根据牵引作用方向逆向调节控制参数,对于系统稳定裕度有一定提升。在相同的临界失稳条件下,系统失稳波形的发散幅度均有所减小甚至消失。表4给出了图11的量化分析结果。

表4 振荡发散程度量化Tab.4 Oscillation divergence quantification
可以看到,参数调节相同比例下,输电线路电感的作用最为明现,可快速将系统镇定。而锁相环带宽的调节作用则强于输电线路电阻,即调节致稳作用:输电线路电感>锁相环带宽>输电线路电阻,这与表3和图7所示灵敏度计算结果顺序一致,进一步验证了指标的有效性。
4 结语
本文提出一种针对风电场振荡的频域网络分析方法,基于所建立节点参与因子指标可确定参与振荡的主导节点。进一步地,利用灵敏度指标确定主导节点处各元件的关键参数,发现锁相环带宽以及电网内阻抗是引起失稳的重要因素,从而实现了对风电场失稳要素的多级定位。同时,观察各关键参数在复平面上对失稳模式的牵引作用,可指导控制器参数调节的对象及方向。该方法有助于诊断实际风电场中易出现谐振风险的薄弱风机或参数,从而提前制定针对性的稳定调整措施,降低系统的失稳风险。

