巧用类比思想,培养初中生逻辑推理能力
宿迁市苏州外国语学校 张 诚
法国数学家拉普拉斯认为:“在数学的王国里,发现真理的主要工具就是归纳和类比.”类比推理是指根据两种不同对象在某些方面具有相同之处或相似之处,借助于联想,通过对一个模型的研究来获得另一个模型的信息,常常作为探索新问题的办法.类比推理的科学预见性、探索性,可以让学生经历联想、抽象化、映射、验证等数学活动过程,更有助于学生发现、提出问题,培养学生的创新意识.
1 巧用概念类比,引导合情推理
数学概念是数学重要基石.掌握概念内涵,厘清概念异同点,是学习数学的基础.由于数学概念具有一定的枯燥性、繁杂性和相似性,且很多概念之间存在紧密的联系,故学生在学习时非常容易混淆.在新概念教学时,巧用概念类比,引导学生巩固复习已学概念,并在新旧概念的共同点和差异中明确概念同化的关键要素[1],并将零散的数学知识联结成数学知识链条,有助于完善学生的知识结构体系.
案例1“一元二次方程”概念课
“一元二次方程”是初中数学中的重要内容,可以让学生类比一元一次方程的概念,通过合情推理得到一元二次方程的概念.在课堂中,首先结合学生生活创设以下问题导入新课.
复习引入:一块长方形绿地的周长为34 m,宽为7 m,那么它的长是多少?
学生通过独立解决问题,回顾一元一次方程的概念及利用方程解决问题的方法,为学习一元二次方程做好准备.
概念类比:根据题意,列出方程.
(1)一块长方形绿地的面积为1200 m2,且长比宽多10 m,那么长和宽各为多少m?
(2)一个正方形的面积等于12,求它的边长.
(3)已知一个数比另一个数大3,且两个数乘积为0,求这两个数.
在列方程的过程中,要求学生思考以上三个方程与一元一次方程的相同点,尝试类比一元一次方程给上面的三个方程下定义,其目的是用三个实际问题列出的三个方程与一元一次方程进行类比,理解“元”“次”等特征,从而顺利归纳出一元二次方程的概念:只含有一个未知数且未知数的最高次数为2的整式方程叫做一元二次方程.那么,一元二次方程的一般形式如何呢?还需要对上述两个方程进行一般化,从而得到一元二次方程的一般形式为
ax2+bx+c=0(a≠0),
其中,ax2为二次项,a为二次项系数,bx为一次项,b为一次项系数,c为常数项.

表1 一元二次方程与一元一次方程的类比
在整个教学环节中,将类比推理的思想与一元二次方程概念的学习有机融合起来,教师的不断引导,让学生经过观察、联想、抽象化和映射的数学活动,通过类比推理,从而根据一元一次方程的概念得到一元二次方程的概念,极大程度地锻炼了学生的逻辑推理能力.
2 巧用性质类比,体验推理过程
数学性质是数学表观和内在所具有的特征,是一种事物区别于其他事物的本质属性.性质相似的事物在其他方面也具有一定的类似性,只有掌握数学对象的性质才能更好地运用它解决数学问题[2].由于数学性质之间往往有内在的关系和逻辑关系,新旧性质的类比,可以帮助学生建立知识体系.所以,在学习新的数学对象性质时,可以采用性质类比的方法,引导学生将新的数学对象与旧的数学对象进行比较,在辨析它们之间异同点的过程中,促进新性质的同化,这对于学生逻辑推理能力的培养大有裨益.
案例2“平行四边形与梯形”单元复习课
平行四边形是研究特殊平行四边形的定义、性质和判定的基础.由于该部分知识比较杂乱且分散,因此在单元复习课中,以“整”“理”为主线,结合思维导图引导学生对平行四边形和梯形的性质进行类比复习,帮助学生构建完整的知识体系.
“整”,即让学生在课前自主整理平行四边形与梯形的性质特点,抄写下来,并按照一定逻辑顺序粘贴,其目的是将分散在本单元中的知识要点展现在同一张图上,形成整体(如图1)感知,为性质的类比分析做好铺垫.

图1
“理”,即让学生以小组合作的形式,对平行四边形和梯形的相关性质进行个性化梳理,整理出自己最感兴趣的,认为最重要的或掌握最不扎实的相关知识点.
“复”,即根据学生的“理”与“习”的反馈,有针对性地查漏补缺.发现学生在自主类比复习过程中的薄弱点在平行四边形与梯形以及平行四边形与长方形之间的联系上.同时,学生虽然能够绘制出四边形与各种特殊四边形关系的韦恩图,但对于它们之间的联系却不甚清晰.为此,针对学生存在的问题,设计了以下四个任务:
(1)将1个平行四边形剪成2个梯形;
(2)将1个平行四边形剪成2个完全一样的梯形;
(3)将1个梯形剪出1个平行四边形;
(4)将1个长方形剪出1个平行四边形.
学生以小组挑战的形式完成任务,并进行成果展示,在此过程中教师要注重引导学生关注平行四边形和梯形的主要特征,通过类比分析帮助学生完善思维导图.这样既有利于降低学生学习与记忆难度,而且能让学生亲身体验类比的过程,从中感受数学的逻辑美和知识之间的有趣关联,促进学生类比推理能力的提升.
3 巧用条件类比,推理不变特征
不变特征是类比推理的前提,也是学生在类比推理过程中发现的“新结果”.当遇到一些新的数学习题或问题时,学生往往会根据题目给出的条件,类比已经学习过的知识,从而使得陌生问题熟悉化,当寻找到其不变特征时,问题就能得以顺利解决[3].为此,在初中数学教学中,尤其是在解题教学中,可以引导学生结合所求目标,从条件入手寻找不变特征,大胆猜测、尝试与验证,并在类比的过程中进行适当的探索来解决问题.
案例3解题教学
(1)如图2所示,已知△ABC,以AB,AC为边向外分别作等边三角形ABD和AEC,连接BE,CD,请将图形补充完整,并思考BE,CD之间有什么数量关系?请说明理由.
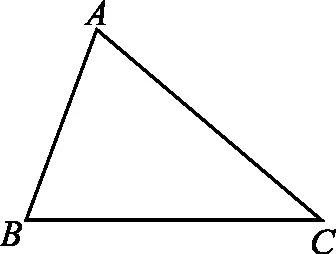
图2
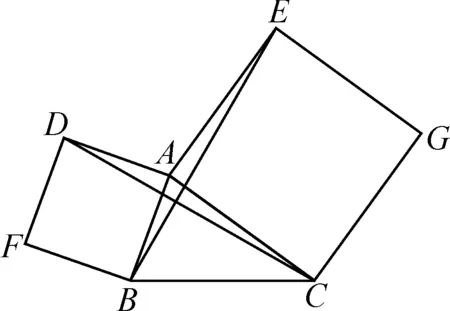
图3
(2)如图3所示,已知△ABC,以AB,AC为边向外分别作正方形ABFD和AEGC,连接BE,CD,并思考BE,CD之间有什么数量关系?请说明理由.
对于题(1),学生根据已知条件,很快画出图形,并分析.由于△ABD和△AEC为等边三角形,所以有AD=AB,AC=AE,∠DAB=∠CAE=60°,可以证明△ACD和△AEB全等.根据三角形全等的性质,可以推导出BE=CD.寻找“全等三角形”是求解本题的关键.
题(1)是向外作等边三角形,而题(2)则是向外作正方形,等边三角形和正方形都属于多边形,且具有各边相等、各内角相等的基本性质.为此,在求解题(2)之前,可以引导学生类比观察两道题目中的已知条件,既然三角形和正方形具有相同的性质特征,由此,可以猜想题(2)与题(1)的解题思路应该是基本一致的.这样类比题(1)的解题思路进行分析,可以看出边与角之间的关系依然成立.由于ABFD和AEGC均为正方形,所以有AD=AB,AC=AE,∠DAB=∠CAE=90°,可以证明△ACD和△AEB依然是全等的,那也就是说结论还是BE=CD.
题(1)与题(2)有着相似的条件,所以,我们可以合理地猜想其条件的相似可能会产生相似的结论[4].这样通过类比条件的方法,可以帮助学生更加迅速、准确地解题,尤其在解决一些抽象的几何问题时.类比推理是一条通往成功的捷径,对学生的数学解题能力与逻辑推理能力的培养来说是非常有益的.
4 巧用方法类比,培养推理能力
很多中学曾提出“数学问题应该‘一看就会,一做就对’”.在数学教学中,过分强调技能训练,会忽视了学生对数学问题的思考,从而导致学生陷入“一看就会,一做就废”的怪圈.学生在教师讲解时往往能听懂,但当他们遇到新的问题时,就会变得束手无策.所以,数学教学应教会学生如何思考问题,在遇到不熟悉的新问题时,可以将这类题目与已知问题解决方式紧密联系起来,运用已解决的数学问题的思想方法来解决新的问题,比如方程思想、数形结合思想、类比思想、化归思想等[5],而这一过程中充分体现了数学思想方法的类比运用.将思想方法类比贯穿于中学数学教学中,对培养学生类比推理能力和解决问题的能力极为重要.
案例4已知一条直线上依次有A,B,C三个点,那么一共有几条线段呢?
这个问题一般学生都能求解,共有三条线段,很多时候我们往往在学生得出答案就结束这个问题了.事实上,如果我们引领学生认真思考并进行知识迁移,学习效果将会截然不同.
思考1:如果这条直线上有6个点,你怎么数出线段的条数呢?
通过思考1,可以得到“顺序识图”的方法:根据线段有两个端点的特征,可以先固定第一个端点,然后再以其余的点作为另一个端点组成线段,然后固定第二个端点,以其余的点组成线段,以此类推,直到找出最后的线段位置.采用一种方法,可以避免遗漏、重复的现象,不难得到当直线上有6个点时,一共有15条线段.
思考2:如果这条直线上有n个点,共有多少条线段呢?
采用思考1中的顺序识图法,学生很快得出,共有(n-1)+(n-2)+……+3+2+1条线段.
思考3:如何计算(n-1)+(n-2)+……+3+2+1呢?
假设
S=(n-1)+(n-2)+……+3+2+1,
①
S=1+2+3+……+(n-2)+(n-1).
②
①+②式,得2S=n(n-1),所以S=0.5n(n-1).
在这个问题的解决过程中,采用了高斯的倒序相加法,这种方法不仅能巧妙解决很多初中数学问题,在高中数学学习中更有用武之地.
思考4:这个方法是否能够迁移运用到其他数学问题中呢?
数角问题:从点O引m条射线OA,OB,OC,……,若组成的角都是锐角,则共有多少个锐角?
握手问题:七年级三班一共有45名学生,若每两人握一次手,一共握了多少次手?
比赛问题:n个篮球队进行单项循环比赛,其中每一个篮球队都必须与其他篮球队赛一场,总比赛场次是多少?
在解决数学问题的过程中,很多数学思想方法都具有一定的相似性.尤其是在解决一些复杂问题时,可以尝试将问题进行分解,运用转化的思想,使其变为我们所熟悉的问题,进而类比已有的解题思路,将各个问题突破,从而在问题解决的过程中,学生的逻辑推理能力能够得到很好的训练.
5 结语
波利亚曾说过:“类比是发现的源泉,是一个伟大的引路人.”逻辑推理能力是重要的数学素养,在数学课堂中,巧用类比思想,可以让学生将旧知识类比迁移运用到新知的学习中,形成新的知识结构和体系,同时,在类比探究过程中,促进了创造力和思考力的升华,提升了学生自主解决问题的能力,有助于提高学生的逻辑推理能力,实现对学生数学核心素养的培养.

