巴特沃斯高通滤波器的优化设计与仿真实现

姚林杰，王耀斌，蒋 伟

（株洲宏达电子股份有限公司，湖南株洲 412011）

0 引言

滤波器是一种选频装置，可以使信号中特定的频率成分通过，且极大地衰减其他频率成分。利用滤波器的这种选频作用，可以滤除干扰噪声或进行频谱分析［1-2］。滤波器可广泛应用于工业、商业和机关团体的配电网中，在人们日常生活中有着不可替代的作用。

滤波器作为一个系统的重要元器件，它的优劣会影响着整个系统的功能和质量［3］。早期的滤波器主要是由无源元件电容、电感和电阻组成的滤波电路。自20 世纪60年代以来，随着集成运放的发展，由集成运放、电容、电阻组成的有源滤波电路得到广泛应用，相比于无源滤波电路，有源滤波电路有着不用电感、体积小、重量轻的优点，所以有源滤波器在几十年间得到了快速发展［4］。

目前，相比于低通滤波器，高通滤波器的探讨与研究较少。开关电容式专用滤波芯片等器件的出现使得高通滤波器的实际应用成为现实［6］。然而，由于其电路存在噪声等因素，会对滤波器的滤波效果产生负面影响。因此，对RC有源高通滤波器进行优化设计的相关研究具有一定的工程应用价值［2］。

本文提出了一种四阶RC 有源巴特沃斯高通滤波器的设计方法，该方法在确定电容和增益的基础上先设计出二阶高通滤波器，然后在此基础上利用低通滤波器与高通滤波器之间的频率转换函数设计四阶巴特沃斯高通滤波器。该设计方法不仅可以使二阶滤波电路系统取得最佳阻尼系数，同时它的网络元器件参数也较易选择。基于该方法设计出的两个四阶巴特沃斯高通滤波器也具有良好的幅频特性。

1 压控电压源式二阶高通滤波电路的设计

常见的二阶高通滤波电路主要有两种形式，即无限增益多路反馈式和压控电压源式［7］。由于压控电压源式电路具有输入阻抗较高且输出阻抗较低的特性，同时所需的精密电阻、电容器件较少，对运放要求也低，故本文采用压控电压源式二阶高通滤波电路作为高阶高通滤波电路的基本单元。其电路原理如图1 所示。

图1 压控电压源式二阶高通滤波电路

可得电路如图2 所示。

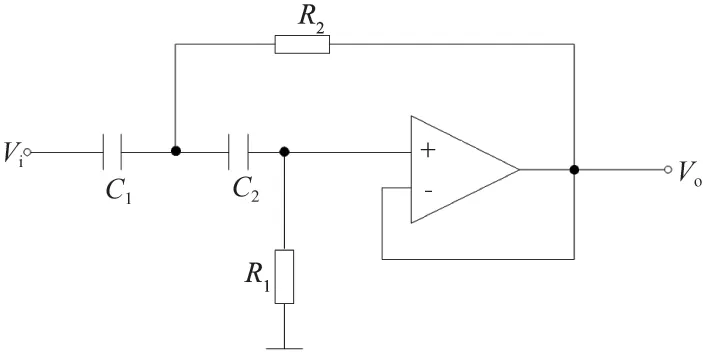
图2 Af＝2 时二阶高通滤波系统电路图

可得电路如图3 所示。

图3 Af＝2 时二阶巴特沃斯高通滤波系统电路图

基于所设计的二阶巴特沃斯高通滤波器电路，利用Multisim14.0 电路仿真软件和Origin 2019 绘图软件得到两个二阶RC 有源高通滤波器的归一化幅频特性曲线如图4 所示。

图4 二阶RC有源高通滤波器的归一化幅频特性曲线

观察图4 可以明显发现相比Af＝2时的幅频特性曲线，Af＝1时的幅频特性曲线更为平坦，且随着频率的增加曲线较为稳定。

至此，已经完成Af不同的取值下的二阶高通滤波电路的设计，接下来将设计高阶巴特沃斯高通滤波器。

2 四阶RC有源巴特沃斯高通滤波器的设计

根据逼近方法的不同，滤波器可以划分为巴特沃斯（Butterworth）滤波器、贝塞尔（Bessel）滤波器、切比雪夫（Chebyshev）滤波器等类型［9］。其中，巴特沃斯滤波器最显著的特点是在通频带内具有最为平坦的幅频特性，且在过渡带内具有单调下降的幅频特性，因此，巴特沃斯得到了广泛的应用［10］。本文基于巴特沃斯滤波器设计四阶RC有源高通滤波器。

设计高通滤波器的方法一般是找到与设计指标相对应的低通滤波器的传递函数，然后通过低通滤波器与高通滤波器之间的频率转换求出高通滤波器的传递函数［8］。已知低通滤波器和高通滤波器之间的转换公式如式（18）所示。

依据线性电路网络理论，有源滤波器的输入输出不会因为级联的原因而产生额外的干扰信号［2］。故可以将二阶高通滤波电路进行级联的方式获得四阶高通滤波电路［11］。

根据第1节所设计的二阶高通滤波单元，可得当时四阶高通滤波系统的电路，如图5所示。

图5 Af＝1时四阶高通滤波系统电路图

当Af＝1时四阶高通滤波系统的电路如图6所示。

图6 Af＝2时四阶高通滤波系统电路图

3 设计实例与仿真

本节将设计一个通带截止频率为100 kHz的四阶RC有源巴特沃斯高通滤波器并开展仿真。

首先在理论上设计当Af＝1时的四阶巴特沃斯高通滤波器，对两个具有相同Af值的二阶巴特沃斯高通滤波器进行级联可以得到一个对应Af值的四阶巴特沃斯高通滤波器［12］。由前面推导的归一化的四阶巴特沃斯高通滤波器的传递函数的公式，第一个二阶巴特沃斯高通滤波器的传递函数为：

然后用Multisim14.0电路仿真软件来仿真设计的四阶巴特沃斯高通滤波器电路，仿真电路图如图7所示。

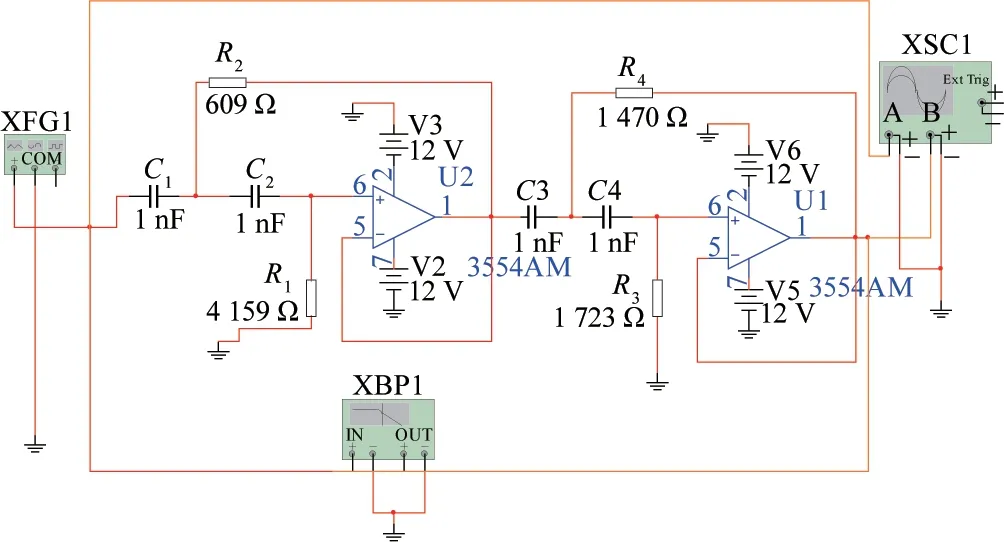
图7 Af＝1 时四阶巴特沃斯高通滤波器的仿真电路

同时利用Origin 2019软件进行数据整理，然后可以得到归一化幅频特性曲线如图8所示。

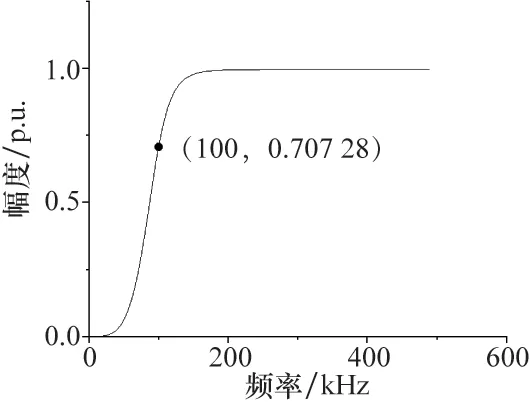
图8 Af＝1 时四阶巴特沃斯高通滤波器幅频特性

同理设计当Af＝2 时的四阶巴特沃斯高通滤波器，由两个具有相同Af值的二阶巴特沃斯高通滤波器进行级联可以得到一个对应Af值的四阶巴特沃斯高通滤波器［12］。由前面推导的归一化的四阶巴特沃斯高通滤波器的传递函数的公式，可以得到第一个二阶巴特沃斯高通滤波器的传递函数为：

与前面所推导的传递函数相对应：

同样地，用Multisim 14.0 电路仿真软件来仿真设计的四阶巴特沃斯高通滤波器电路，仿真电路图如图9所示。

图9 Af＝1 时四阶巴特沃斯高通滤波器的仿真电路

然后利用Origin 2019 软件进行数据整理，可以得到归一化幅频特性曲线如图10 所示。

图10 Af＝2时四阶巴特沃斯高通滤波器幅频特性

最后将设计的两个四阶巴特沃斯高通滤波器的幅频特性曲线放在一起进行比较，如图11 所示。

图11 不同增益的四阶巴特沃斯高通滤波器幅频特性对比

观察图11，可以发现不同于图4，这两个四阶RC有源巴特沃斯高通滤波器的幅频特性曲线几乎一致，不仅更加稳定，且都满足设计要求，即在100 kHz 处幅度为0.707 p.u.左右［14］。仿真结果证明，同样的设计方法，不同增益下的二阶高通滤波器的幅频特性曲线具有明显差异，而本文设计的四阶RC 有源巴特沃斯高通滤波器可以得到具有几乎重合的幅频特性曲线。相比之下，增益为1 时，使用的网络元器件相对较少，设计相对更加简单。

4 结束语

本文通过确定电容和增益的方式先设计二阶高通滤波器，然后在二阶高通滤波器的基础上，利用低通滤波器与高通滤波器之间的频率转换函数算出四阶巴特沃斯高通滤波器传递函数的表达式，提出可以通过将二阶高通滤波电路进行级联的方式获得四阶巴特沃斯高通滤波器。最后设计一个通带截止频率为100 kHz 的四阶巴特沃斯高通滤波器并通过仿真实现。

本文方法计算简单，网络元器件的选择方便快捷，并且最后的仿真结果显示设计的四阶RC 有源巴特沃斯高通滤波器的滤波特性都较好，都能满足设计要求。