鞋楦特征驱动的鞋底模型个性化定制变形*

章 洋，黄常标※，左远征

（1.华侨大学福建省特种能场制造重点实验室，福建厦门 361021；2.华侨大学厦门市数字化视觉测量重点实验室，福建厦门 361021）

0 引言

研究证明，足部健康状况与鞋的穿着情况密切相关[1]，而长期穿着不合人脚生理情况的鞋，既会产生不舒服感又会严重影响人脚骨骼的发育和成形；对于有足部疾病的人，穿着不合适的鞋甚至会恶化其症状。因此针对不同个体的个性化定制鞋底研究十分具有必要性。传统的个性化定制方式主要有纯手工定制和基于CAD/CAM软件辅助定制等方式，这些方式费用昂贵，效率低下。而数字化设计技术的发展使得各种个性化定制的成本大大降低，并使其制作效率极大提高。在现代社会的主观需求和客观因素的双重作用下，针对个性化定制鞋底的研究具有十分重要意义。

个性化定制鞋底主要包括两大流程：（1）利用3D扫描技术得到个人的脚部模型，再提取脚部模型特征数据驱动标准鞋楦变形获得个性化鞋楦模型；（2）基于个性化鞋楦模型驱动现有款式的鞋底模型变形获得个性化定制鞋底模型。目前针对鞋底模型变形的研究较少，绝大多数的模型变形研究主要围绕模型变形的通用性进行研究，针对鞋底模型个性化定制变形可以分为3 个流程，分别是特征提取、模型匹配和模型变形。在经过特征提取、模型匹配后，鞋楦模型和鞋底模型在空间上满足一定的位姿约束，使之符合现实情况的匹配要求，随后在此基础之上，根据鞋楦模型的相关特征对鞋底模型进行变形，从而达到鞋底个性化定制变形的目的。本文主要围绕鞋底模型变形部分开展相关研究，在完成特征提取和模型匹配的基础之上，将径向基函数插值应用于鞋底模型变形，并通过变形策略优化径向基函数插值稳定性问题，有效实现了鞋底模型的个性化定制变形。

1 相关工作

网格模型的变形一直是研究热点，并且有了较为成熟的研究成果，常见的变形技术有空间变形技术、骨架驱动变形技术、多分辨率变形技术以及曲面变形技术等。

空间变形技术的基本原理是将模型嵌入几何空间之中，然后通过变形函数控制几何空间的顶点移动，间接带动几何空间中的模型顶点发生移动，从而实现模型的变形[2-3]。空间变形技术具有操作简便，灵活性强等优点，然而局部区域的变形精度难以控制，变形较大的场合容易导致几何细节丢失。

骨架驱动变形技术的基本原理就是为网格模型建立一个骨架，并按照一定权重设计把骨架与模型顶点关联起来，通过调整骨架位置的方式实现模型变形[4-5]。骨架驱动变形技术简单直观，能够模拟具有骨骼结构的生物动作，但是不适合难以建立骨骼结构的模型，同时对构建骨架时的权重设置敏感性较强。

多分辨率变形技术的基本原理是将模型分为高频和低频两部分，高频部分保存复杂的几何细节，低频部分保存简单的全局特征，变形时针对低频部分进行变形，保持高频部分不变[6-7]。多分辨变形技术能够较好地保留局部细节，但是处理几何细节较多的复杂模型时，分解与重构的工作量巨大，难以承受。

曲面变形技术的基本原理是从网格模型中选择一部分区域作为控制区域，选择一部分区域作为变形区域，当控制区域发生变形时，根据相应的优化目标函数对变形区域的变形情况进行推导，从而得出变形区域的形变量[8-10]。曲面变形技术的操作更加简单直观，可以直接对网格模型进行变形操作，变形精度更高，其次可以通过约束来保持局部的几何细节。但是曲面变形技术的缺点是它们在计算代价和数值稳定性上与网格的复杂度密切相关。

因为空间变形技术变形精度难以控制，鞋底模型不适合添加骨架，多分辨变形技术计算量大，因此本文采用了基于径向基函数（Radial Basis Function）插值的变形方法来进行鞋底模型变形，该方法原理与曲面变形技术相似，都是直接对模型进行变形操作，变形精度较高，同时径向基函数插值形式简单，相对于引入各种约束的曲面变形技术更加简洁，计算效率更高。Hardy[11]最早提出了Multiquadric函数，并将其应用于地貌形状与飞机外形设计的曲面拟合问题，标志着径向基函数插值应用的开端。现在，径向基函数插值已经大量的应用于医学图像的弹性配准，曲面重建，人脸变形，地质学等方面的研究[12-14]。因此，本文提出了一种基于径向基函数插值的鞋底模型变形方法，该方法将径向基函数插值应用于鞋底模型变形之中，先根据鞋楦模型相关特征对鞋底模型部分区域进行变形，然后使用径向基函数插值拟合鞋底变形曲面，从而实现了鞋底网格模型变形。同时，由于径向基函数作用半径难以确定，导致径向基函数稳定性难以保证，针对径向基函数这一特点以及鞋底模型变形特点，本文从变形策略的角度出发，通过采用合适的变形策略，解决径向基函数插值变形方法稳定性不足问题。

2 鞋底变形的前期工作

本文的鞋楦与鞋底模型为STL 模型，同时采用了半边数据结构来构建三角网格模型的拓扑信息。

本文所研究的鞋底模型变形是在鞋楦和鞋底模型特征提取、模型匹配的基础上开展的。因此，鞋楦和鞋底模型的相关特征已经提前提取，鞋楦和鞋底模型的初始位姿状态也已经提前确定。

在特征提取部分，根据鞋底模型变形算法的要求，针对鞋楦模型，已经提取了鞋楦脚线、鞋楦底面中轴线，如图1所示；针对鞋底模型，提取了鞋底内仁线、鞋底模口线和鞋底内部中轴线等特征，以鞋底模口线为分界线可以将鞋底模型划分为内部区域和外部区域，如图2所示。

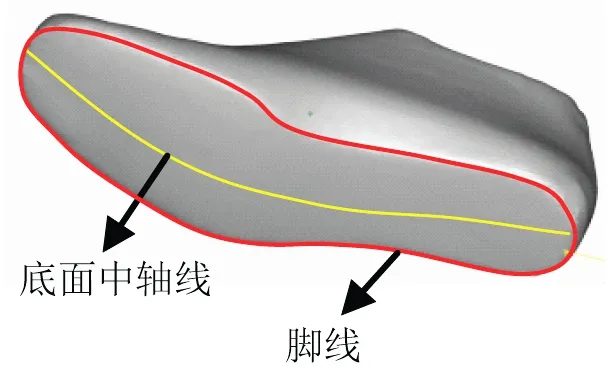
图1 鞋楦模型

图2 鞋底模型

在模型匹配部分，已经根据相关约束完成了鞋楦模型与鞋底模型的位姿调整，使其符合现实情况下鞋楦和鞋底模型的位姿关系，并且将鞋楦模型和鞋底模型的长、宽、高方向与世界坐标对齐，使之有了具体的参考方向。鞋楦模型和鞋底模型的具体位姿关系如图3所示。

图3 鞋楦与鞋底的位姿关系

3 鞋楦特征驱动的鞋底模型变形

本文采用径向基函数插值的方法来进行鞋底变形，但是，径向基函数插值方法的稳定性将严重影响变形的精度，因此，本文根据径向基函数的特点以及鞋底模型变形的特点，从变形策略的角度出发，通过采用合适的变形策略，解决了径向基函数插值在鞋底模型变形中所暴露的问题。

直接将径向基函数插值应用于三维空间中，稳定性难以保证，但是将三维模型在二维空间进行变形，则可以保证另外一个维度的稳定性，因此，本文将鞋底模型的变形拆分为4 个步骤，预先统一设定鞋楦与鞋底内部区域的间隙距离为t，依次变形如下：（1）水平维度的鞋底模型变形；（2）竖直维度的鞋底模型变形；（3）鞋底模型内部区域的变形；（4）鞋底模型外部区域适应性变形。其中，在进行鞋底模型变形前，鞋楦模型和鞋底模型位姿已经匹配，鞋楦模型和鞋底模型的宽度、长度和高度方向已经统一，且与世界坐标O-XYZ方向已经对齐，X对应宽度方向，Y对应长度方向，Z对应高度方向，因此，本文变形步骤中的水平维度为XOY平面，竖直维度为YOZ平面，鞋楦模型底面中轴线和鞋底模型内部区域底面中轴线都在YOZ平面内。

3.1 基于径向基函数插值变形原理

径向基函数是一种以样本到数据中心之间的径向距离为参数的标量函数。基于径向基函数插值变形原理是根据控制点之间的几何关系拟合曲面，随后以变形点与控制点的几何距离为驱动，代入拟合曲面之中，反求变形点位移量[15,16]。其基本步骤如下：

（1）选择合适变形区域，选取特征点作为控制点，选取其余点作为变形点；

（2）根据模型变形的要求，计算出控制点的位移量；

（3）选择合适的径向基函数作为计算函数；

（4）计算控制点之间的径向基函数值，根据径向基函数值与控制点的位移量，建立空间节点位移的径向基函数插值模型，并求解坐标分量权重系数；

（5）计算控制点与变形点之间的径向基函数值，根据径向基函数值和上面求取的坐标分量权重系数反求变形点的位移量；

（6）原变形点加上各自对应的位移量，即可得到变形后的模型。

3.2 鞋底模型变形步骤

3.2.1 级放处理

由于鞋楦模型源自用户脚部数据，而鞋底模型源自企业模型库，两者尺寸大小往往存在一定的误差，需要根据鞋楦模型长度与宽度尺寸对鞋底的尺码进行校正，进而减少后续变形操作的变形量，提高精确度。

进行级放处理时尽量保持鞋底模型纹理形状等局部特征和位姿关系不变，因此，将鞋楦模型底面中轴线和鞋底模型内部中轴线投影在水平面，将两条投影线的首尾余量作为间隙余量，根据间隙余量确定缩放中心和缩放比例，计算方法如下。

（1）在水平面上，点a为鞋底中轴线头部端点、点b为鞋楦中轴线头部端点、点c为鞋楦中轴线尾部端点、点d为鞋底中轴线尾部端点。设点o为水平面上的缩放中心点，设l1=a-o、l2=d-o、l3=b-o、l4=c-o、则满足条件：l1/l3=l2/l4，从而计算出水平面上的缩放中心点o。如图4所示。

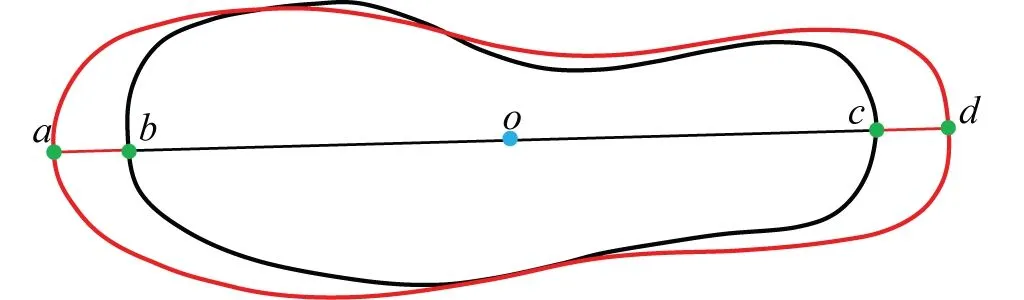
图4 级放处理

（2）将水平面上的缩放中心点o沿鞋底模型高度方向z投影回鞋底内部区域底面，即可得到三维空间中的缩放中心点p，缩放比例为｜｜l1｜｜/｜｜l3｜｜。

3.2.2 鞋底模型水平维度的变形

该过程以鞋楦模型脚线作为驱动，驱动鞋底模型内仁线和模口线变形，从而带动整个鞋底模型发生变形，使鞋底模型适应鞋楦脚线水平轮廓特征。具体变形流程如下。

（1）将已提取的鞋楦模型脚线、鞋底模型内仁线与鞋底模型模口线投影到长度方向Y和宽度方向X所组成的水平面上得到三者的水平投影线，如图5所示。

图5 鞋底模型水平维度的变形

（2）为提高后续径向基函数插值的稳定性，对鞋楦脚线的水平投影线上的点进行均匀采样，经过采样筛选后的顶点之间的欧氏距离大小相近，分布更加均匀。

（3）设采样后鞋楦脚线的水平投影线上的点为a，利用PCA 算法可以计算点a的法线方向N并单位化，但是无法确定方向的正负，因此设o为鞋楦脚线点的数据中心点，设向量l1=a-o，若N·l1≥0，则N为正方向，反之则为反方向，需要进行反向处理，如图5 中N为正方向，不需要反向处理。

（4）由点a计算出鞋底模型内仁线和模口线的控制点和形变量（形变量为向量），具体为：延长鞋楦脚线点a的法线方向N，分别交鞋底模型内仁线和模口线的水平投影线于b和c，如图5 中A、B两种情况，A情况时鞋楦与鞋底发生干涉，B情况时鞋楦与鞋底存在间隙。将b作为鞋底模型内仁线的控制点，c作为鞋底模型模口线的控制点，设向量l2=b-a，根据间隙距离值t，计算控制点b的形变量Vb=N×t-l2，为保证鞋底模型内部侧壁特征不变，控制点c的形变量保持和控制点b一样的形变量，则控制点c的形变量Vc=Vb。

（5）重复计算出所有的控制点及其形变量，将鞋底模型的所有顶点作为变形点，根据均化处理时设置的间隔距离，设置合适的径向基函数作用半径，本文采用的径向基函数为Wendland’sC2函数，采用径向基函数插值计算出变形点水平维度的位移量，鞋底模型顶点加上各自对应的位移量，完成水平维度的鞋底模型变形。

3.2.3 鞋底模型外部区域竖直维度的变形

竖直维度的变形为鞋底模型外部区域的变形。以鞋楦底面中轴线点作为驱动，驱动鞋底外部底面区域的中轴线变形，从而带动整个鞋底模型外部区域发生变形，使鞋底模型外观适应鞋楦中轴线特征。具体流程如下。

（1）用平面YOZ切割鞋楦和鞋底模型，得到鞋楦和鞋底在竖直方向上轮廓线，如图6 所示，图中红色线段为鞋楦模型底面中轴线，蓝色线段为鞋底模型内部底面中轴线，绿色线段为鞋底模型外部底面轮廓线。

图6 鞋底模型竖直维度的变形

（2）由于鞋楦模型底面和鞋底模型内部底面在Z方向间隙太大，为避免下一步鞋底内部区域的变形中，对鞋底内部区域结构造成过大的破坏，需要将鞋楦模型沿Z方向移动d。设鞋楦底面中轴线头部端点为p、鞋底内部底面区域中轴线头部端点为q、向量l1=p-o、向量l2=p-o，则移动距离d=l1·Z-l2·Z，若d＞0，则沿Z方向移动，若d＜0，则沿Z反向移动，如图6（b）所示。

（3）为提高后续径向基函数插值的稳定性，对鞋楦底面中轴线点进行均匀采样。

（4）设均匀采样后鞋楦底面中轴线上的点为a，过点a做平行Z方向的直线与鞋底交于b、c两点，将点c作为控制点。为保证鞋底厚度尽量不做改变，即控制b、c两点之间距离不变，设向量l3=b-a，向量Vz为Z方向的单位向量，根据间隙距离t，计算出控制点c的形变量Vc

=Vz×t-l3。

（5）重复计算出所有的控制点及其形变量；将鞋底模型外部区域的所有顶点作为变形点，设置合适的径向基函数作用半径，采用径向基函数插值计算出变形点竖直维度的位移量，鞋底模型外部区域的顶点加上各自对应的位移量，完成竖直维度的鞋底模型外部区域变形。

3.2.4 鞋底模型内部区域的变形

完成鞋底模型外部区域变形后，以鞋楦模型顶点为驱动，驱动鞋底模型内部区域发生变形，使得鞋底模型内部区域符合鞋楦模型的曲面特征约束，具体流程如下。

（1）计算鞋楦模型所有顶点的单位法矢N，筛选有效驱动顶点。对于任一鞋楦顶点，沿其顶点法矢方向N的射线与鞋底模型内部区域有交点，则为有效驱动顶点，如图7 所示，黑色线为鞋楦模型，蓝色线为鞋底内部区域，点a为无效驱动顶点，点b为有效驱动顶点。为提高求交计算效率，对鞋底模型内部区域建立八叉树数据结构，加速有效驱动顶点的筛选。

图7 鞋底模型内部区域的变形

（2）为提高后续径向基函数插值稳定性，对有效驱动顶点进行均匀采样。

（3）计算采样顶点b沿其单位法矢方向N的射线与鞋底模型内部区域的交点c，将c作为控制点，设向量l1=c-b，根据间隙距离t，计算控制点c的形变量Vc=N×t-l1。

（4）重复计算出所有的控制点和形变量，将鞋底模型内部区域的所有顶点作为变形点，设置合适的径向基函数作用半径，采用径向基函数插值计算出变形点的位移量，鞋底模型内部区域的顶点加上各自对应的位移量，完成鞋底模型内部区域变形。

3.2.5 鞋底模型外部侧壁区域适应性变形

上一步中鞋底内部区域发生了变形，因此鞋底外部侧壁区域需要根据内部区域变形情况进行适应性变形。该过程以鞋底模口线为驱动，驱动鞋底外部区域侧壁部分发生变形。为保证鞋底侧壁高度不变，只在水平维度上进行适应性变形。具体流程如下。

（1）为了提高后续径向基函数插值的稳定性，对鞋底模型模口线上的点进行均匀采样。

（2）设鞋底内部变形前的鞋底模型模口线上的顶点为a，将a作为控制点，设变形后的鞋底模型模口线上的顶点为b，设向量l1=b-a，向量Vz为Z方向的单位向量，同时，因为只在水平维度上进行变形，如图8 所示，则控制点a的形变量Va=l1-Vz×（l1·Vz）。

图8 鞋底模型外部区域适应性变形

（3）重复计算出所有的控制点和形变量，将鞋底模型外部侧壁区域的顶点作为变形点，设置合适的径向基函数作用半径，采用径向基函数插值计算出变形点水平维度的位移量，鞋底模型外部区域的顶点加上各自对应的位移量，完成鞋底模型外部区域适应性变形。

完成所有变形步骤后，无论是鞋底模型的内部区域还是鞋底模型的外部区域都将适应鞋楦模型的特征。

4 实验验证

为验证本文算法的有效性，在Windows 平台VC++2017 环 境 下，IntelⓇCore（TM）i7-9700 3.00 GHz CPU，16GB内存PC机上实现本文算法，实验效果如下所示。

对比图9 和图10 可知，级放处理后鞋楦模型与鞋底模型尺码关系更加准确，同时鞋楦模型与鞋底模型的位姿关系依旧保持良好，但图10 显示，鞋底模型与鞋楦模型有着较大的差距。

图9 级放处理前的模型

图10 级放处理后的模型

经测试，均化处理时的间隔距离设置为5 mm时，径向基函数的作用半径设置为100～150 mm，变形效果和稳定性较好。对比图11和图12，在个性化变形后的鞋底模型的外部区域特征更加适应鞋楦模型的形体特征，鞋底模型的整体形状外观更符合个性化定制的要求。并且该个性化变形效果良好，鞋底模型不会出现拉伸、撕裂和扭曲等错误现象，同时在符合变形要求的基础之上，尽可能保持了鞋底模型的纹理特征。

图11 个性化变形前的模型

图12 个性化变形后的模型

为验证鞋底模型内部区域能否适应鞋楦模型的特征，对个性化变形后的鞋楦模型和鞋底模型进行切片，如图13和图14。图13中依次为变形后鞋楦模型和鞋底模型在x=-20 mm、x=0 mm、x=20 mm 三个截面上的切片轮廓；图14中依次为变形后鞋楦模型和鞋底模型在y=60 mm、y=120 mm、y=180 mm 三个截面上的切片轮廓。图13～14显示个性化变形后的鞋楦模型和鞋底模型的切片轮廓在两者接近处的法向间距较为均匀，说明个性化变形后的鞋底模型内部区域更加适应鞋楦模型的曲面特征，达到个性化定制的适应脚部特征的要求。

图13X方向切片轮廓

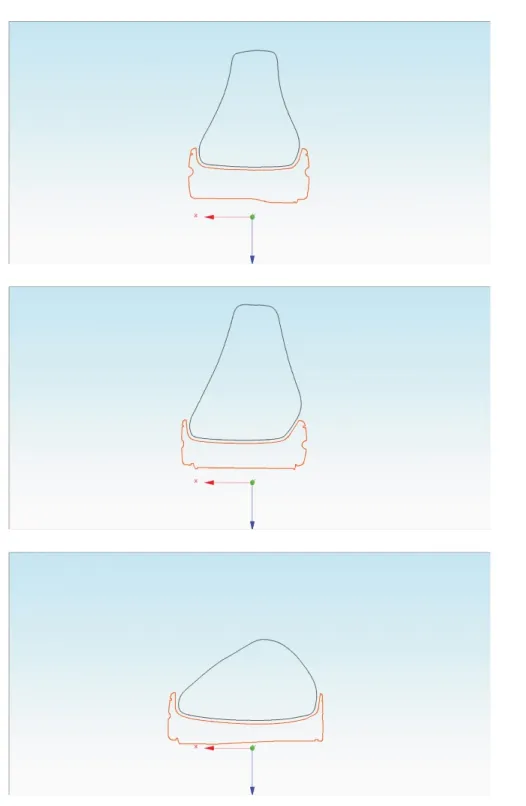
图14Y方向切片轮廓

为进一步验证算法的健壮性，在同样实验环境下做了第二个鞋底模型的个性化定制变形实验，实验效果如图15～18 所示。对比图15 与图16，显示变形后第二个鞋底模型的形体特征也能够很好地匹配鞋楦模型的特征。

图15 个性化变形前的模型

图16 个性化变形后的模型

图17 中依次为变形后鞋楦模型与鞋底模型在x=-20 mm、x=0 mm、x=20 mm 三个截面上的切片轮廓；图18 依次为变形后鞋楦模型和鞋底模型在y=-70 mm、y=-20 mm、y=30 mm 三个截面上的切片轮廓。图17～18显示个性化变形后的第二个鞋底模型的内部区域也更加适应鞋楦模型的曲面特征。

图17X方向切片轮廓

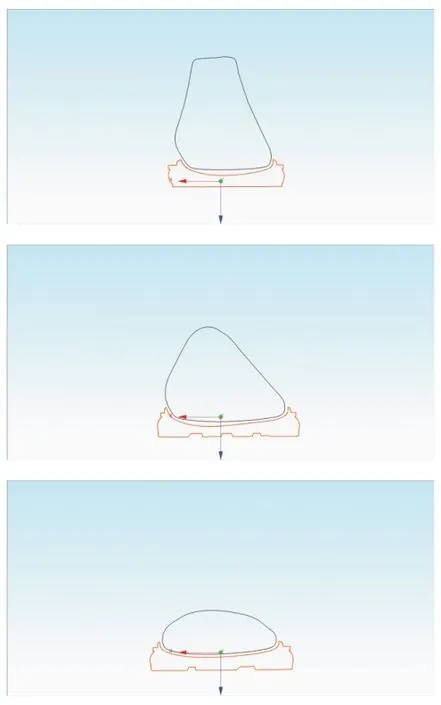
图18Y方向切片轮廓

为进一步验证鞋楦模型与鞋底模型内部区域的法线方向的间隙余量是否达到变形后的设计要求，在图12所示鞋底模型变形后，对鞋楦模型顶点进行随机采样，计算采样点沿其法线方向到鞋底模型内部区域的间隙余量，将其作为评价变形效果的指标。如图19 所示，黄色线段为变形前的间隙余量，差异较大，说明鞋底模型内部区域不符合鞋楦模型曲面特征约束。而蓝色、绿色和橙色线段分别为预设的间隙距离值t=2.0 mm、t=3.5 mm 和t=5.0 mm 时变形后的实际间隙余量，可以发现变形后的间隙余量与预先设定的间隙距离值的差值误差在±1 mm 之内，表明变形后的鞋底模型内部区域比较贴合鞋楦模型的曲面特征，且蓝色、绿色和橙色线段的波动性不大，反映变形也较为稳定，因此本文鞋楦特征驱动的鞋底模型个性化定制变形方法能够根据鞋楦模型的特征有效地实现鞋底模型的个性化定制变形，变形效果较为良好。

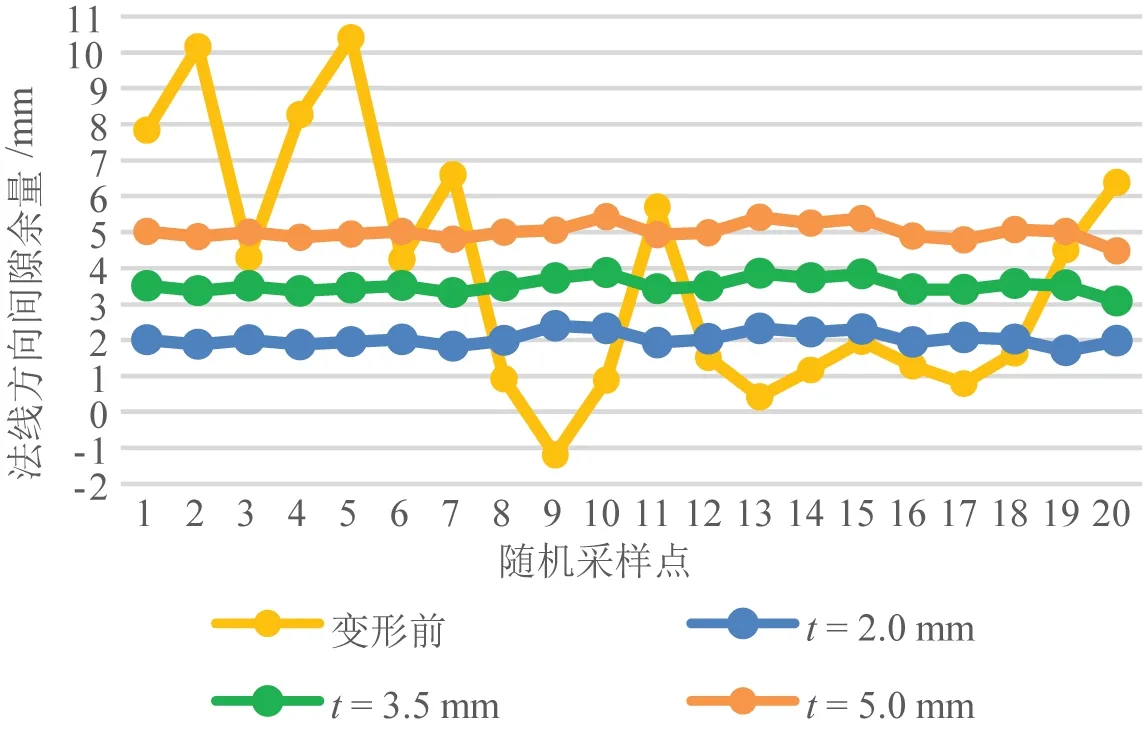
图19 随机采样点的法线方向间隙余量

5 结束语

本文提出了一种基于径向基函数插值的鞋底模型变形方法。由于径向基函数作用半径难以确定，导致径向基函数稳定性难以保证，针对径向基函数这一特点以及鞋底模型变形特点，本文从变形策略的角度出发，通过采用合适的变形策略，解决径向基函数插值方法在鞋底模型变形中所暴露的问题。本文为实现鞋楦模型特征数据驱动的鞋底模型复杂变形，在鞋底模型级放后将鞋底模型变形过程分为4个步骤，即鞋底模型水平维度变形、鞋底模型外部区域的竖直维度变形、鞋底模型内部变形、鞋底模型外部侧壁部分的变形；每次变形中，选择合适的控制点及变形量后，利用径向基函数插值方法进行变形。算法实例表明本文的变形策略能够有效实现较为精确的鞋底变形控制，使得鞋底模型适应个性化鞋楦特征。

目前针对鞋底模型个性化定制变形的研究较少，但是鞋底个性化定制对于人体健康和提高企业竞争力具有重要意义。本文提出的鞋底模型个性化定制变形方法具有较好的可行性和有效性，但与实际的鞋底模型设计过程中采用特征参数不一样，因此穿着舒适性有待进一步验证。